直接分析法在索结构设计中的应用

于 征，薛素铎，王立军

(1 北京工业大学建筑工程学院， 北京 100124； 2 中冶京诚工程技术有限公司， 北京 100176；3 华诚博远工程技术集团有限公司， 北京 100052)

0 引言

近年来，为应对国家有关大气污染物防治的环保政策要求，各地大面积露天煤矿料场开始陆续采用大跨度空间网格结构进行料场封闭。

大跨度空间网格结构的设计通常基于《钢结构设计标准》(GB 50017—2017)[1](简称新钢标)、《空间网格结构技术规程》(JGJ 7—2010)[2](简称空间网格规程)、《拱形钢结构技术规程》(JGJ/T 249—2011)[3](简称拱形钢结构规程)等相关标准(规范)。其中，结构的稳定性设计包括传统的计算长度法和新钢标引入的直接分析法。

目前，广泛应用的几种结构设计软件都已将直接分析法引入设计模块当中。其中，技术相对成熟的是香港理工大学开发的NIDA软件。陈绍礼等[4]通过结构算例验证了NIDA软件中直接分析法的有效性，指出直接分析法相对于计算长度法有更高的可靠性，能克服计算长度法由于计算长度取值的不安全或保守所导致的工程设计上的失误或浪费。刘耀鹏等[5]将改良的基于力法的可直接考虑构件几何初始缺陷和残余应力的高性能梁柱单元整合入NIDA软件，采用时程分析法讨论直接分析法在抗震设计中的运用，提出直接分析法抗震设计的基本框架。舒赣平等[6]利用NIDA软件对3组半刚性连接框架结构进行直接分析，并与试验结果进行对比，验证了直接分析法对半刚性连接钢框架进行结构分析的有效性和可靠性。此外，其他学者对于直接分析法在分析软件和设计实践中的应用也进行了研究[7-10]。

本文以既有的含预应力索的150m跨度空间拱桁架结构为例，分别以3D3S软件采用计算长度法和以NIDA软件采用直接分析法对结构进行稳定性设计。通过分析结果，讨论直接分析法对结构用钢量的优化效果。

1 新钢标关于稳定性设计的规定

本章节对新钢标中与空间拱桁架结构有关的结构设计规定进行阐述。

1.1 结构分析

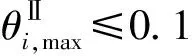
(1)

式中ηcr为整体结构最低阶弹性临界荷载与荷载设计值的比值。

由于大跨度空间结构的失稳模态具有整体性，传统的基于构件稳定的计算长度法并不适合其稳定性分析，故新钢标第5.1.9条要求大跨度空间网格结构设计时，应采用二阶弹性分析或直接分析。

当采用二阶弹性分析时，结构的二阶P-Δ效应可按近似的二阶理论对一阶弯矩进行放大来考虑。然而新钢标仅给出了无支撑框架结构的弯矩放大方法，对于空间网格结构，可以通过采用考虑几何非线性的有限元分析来考虑结构二阶P-Δ效应。

1.2 稳定性计算

1.2.1 计算长度法

新钢标给出了双向压弯圆管的整体稳定计算公式，即式(2)～(7)。

(2)

(3)

β=βxβy

(4)

(5)

(6)

(7)

式中：φ为轴心受压构件的整体稳定系数；N为计算截面处的轴力设计值；A为构件的毛截面面积；f为材料的抗拉、抗压和抗弯强度设计值；M为计算双向压弯圆管构件整体稳定时采用的弯矩值；MxA，MyA分别为构件A端关于x轴、y轴的弯矩；MxB，MyB分别为构件B端关于x轴、y轴的弯矩；β为计算双向压弯整体稳定时采用的等效弯矩系数；M1x，M2x，M1y，M2y分别为x轴、y轴端弯矩(构件无反弯点时取同号，有反弯点时取异号，且︱M1x︱≥︱M2x︱，︱M1y︱≥︱M2y︱)；NE为根据构件最大长细比计算的欧拉力；γm为圆形构件的截面塑性发展系数；NEx′为参数，其值为π2EA/(1.1λx2)。

轴心受压构件的整体稳定系数φ是根据构件的计算长度确定的。对于采用相贯节点的立体桁架结构的杆件计算长度，现阶段是参照空间网格规程及拱形钢结构规程规定，弦杆及支座腹杆的计算长度取1.0l，腹杆计算长度取0.9l(l为节点中心间距离)[2-3]。

1.2.2 直接分析法

采用直接分析法对结构进行稳定性分析时，需要将结构整体初始几何缺陷与杆件初始缺陷建入分析模型中。根据新钢标的第5.5.10条规定，整体初始几何缺陷可采用结构在对应荷载组合下的最低阶整体屈曲模态作为初始缺陷形状。对于大跨度空间网格结构而言，最大位移点的位移可设置为结构跨度的1/300。另外，杆件初始挠曲缺陷δ0可采用式(8)所示的半周期正弦曲线进行假定。

(8)

式中：l为构件总长度；e0为构件中点处的初始变形值，轧制圆管截面可取l/400；x为离构件端部的距离。

将整体初始几何缺陷和构件初始缺陷建入计算模型进行内力和位移的计算，并将所得内力代入式(9)中进行稳定性验算。

(9)

式中：MxⅡ，MyⅡ分别为构件绕x轴、y轴的二阶弯矩设计值，可由结构分析直接得到；Mcx，Mcy分别为构件绕x轴、y轴的受弯承载力设计值。

2 工程设计

2.1 工程概况

为讨论在大跨度空间网格结构设计中采用直接分析法设计与计算长度法设计时的不同，采用天津某封闭煤料场作为设计案例，对该结构进行整体建模和杆件应力比计算。该煤料场结构形式为含预应力索的横向跨度为155m的立体拱形桁架结构，如图1所示。

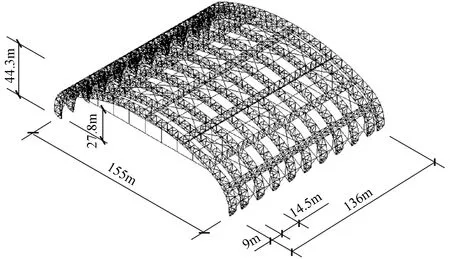
图1 算例煤料场结构示意图

根据实际工程设计资料，工况依照《建筑结构荷载规范》(GB 50009—2012)考虑恒载(0.3kN/m2)，活载(不上人屋面0.5kN/m2)，雪荷载(基本雪压0.4kN/m2、考虑全跨均布雪荷载、半跨均布雪荷载以及三种全跨不均匀分布雪荷载)，风荷载(基本风压0.6kN/m2，考虑左风、右风、山墙风)，温度作用(±30℃)；根据《建筑抗震设计规范》(GB 50011—2010)(简称抗规)，设计地震分组为第二组，场地土类别为Ⅳ类，抗震设防烈度为8度，设计基本地震加速度为0.20g。

案例先按照计算长度法，采用3D3S软件进行截面满应力设计；再按照直接分析法，采用NIDA软件进行截面稳定性校核，若杆件截面尚存在优化空间，则采用直接分析法进行杆件截面优化，从而明确直接分析法对于结构用钢量可达到的优化程度。钢管截面从下列热轧无缝钢管截面中选用：φ89×3.75，φ114×3.75，φ140×3.75，φ159×4.5，φ180×6，φ219×6，φ180×8，φ219×8，φ245×8，φ273×8，φ325×8，φ219×10，φ245×10，φ273×10，φ325×10，φ377×10，φ245×12，φ273×12，φ325×12，φ377×12，φ402×12，φ245×14，φ273×14。

索中预拉力设定为700kN。初始预拉力选取的原则为：1)施加钢索预应力后，跨中挠度在恒载作用下位移不超过100mm; 2)在所有工况组合下，索中始终存在拉力，不发生松弛失效。

以本工程为例，对整体模型采用3D3S软件通过不断试错的方法寻找钢索适宜的初始预拉力。计算后得出：当给钢索施加700kN索力时，索在所有工况组合下不失效，且恒载作用下的跨中挠度为77mm，满足上述初始预拉力选取原则。

另外，由于含有预应力索的空间网格结构设计存在几何非线性的问题，必须采用静力非线性模块进行计算。而对于非线性下的地震组合效应计算，3D3S软件对于刚度较大的结构，采用线性模块下的振型分解反应谱法结果与非线性模块下的静力计算结果相叠加的方式。NIDA软件则是采用时程分析法对结构进行地震效应下的设计计算，而地震波则是根据抗规5.1.2条的规定，选择2条天然波与1条人工波。对于该工程，计算得出结构前3阶自振周期分别为1.787，1.004，0.916s，将所有备选波的最大加速度值放大至70cm/s2，并用SeismoSignal软件计算备选波在这些周期点上的加速度反应谱值，从中选出符合抗规条文要求的天然波Northridge-N41W(简称天然波N41)、Northridge-S49W(简称天然波N49)和人工波T41。3条地震波的加速度反应谱值如表1所示，加速度时程曲线如图2所示。

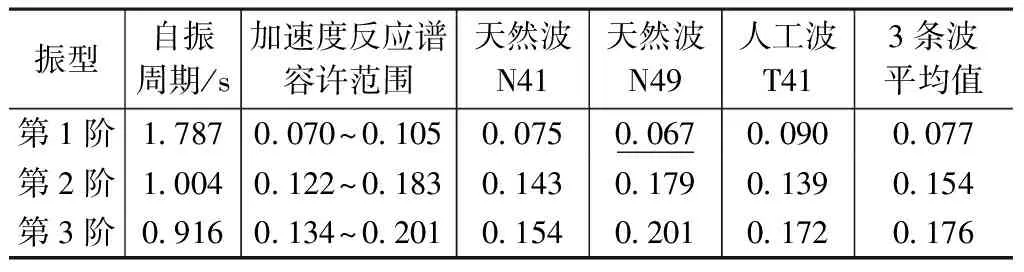
地震波在前3阶周期点上的加速度反应谱值 表1

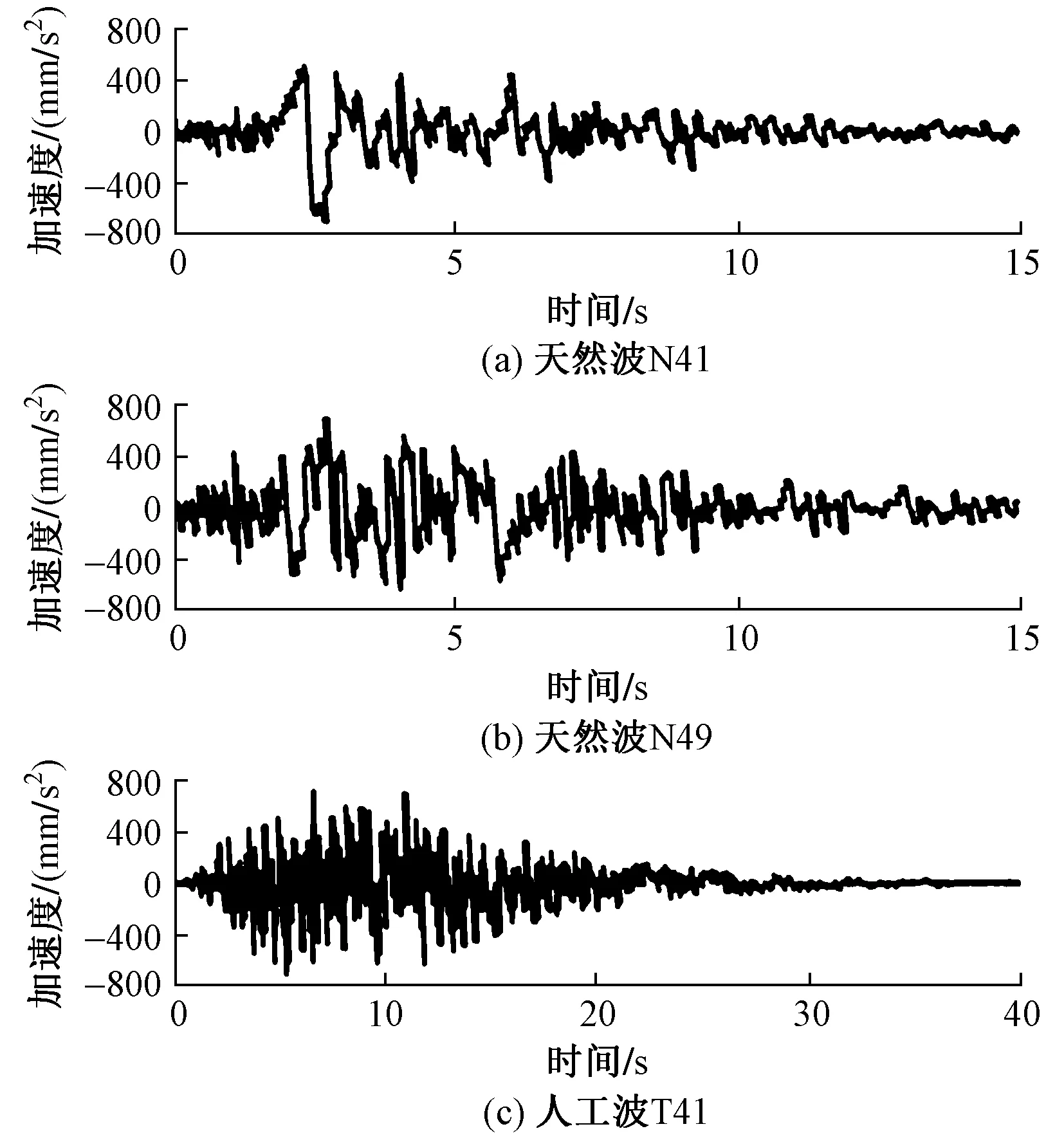
图2 地震波加速度时程曲线

2.2 分析模型

采用3D3S软件对整体空间结构进行建模。杆件节点采用相贯节点，假定为刚接进行设计计算；预应力索与结构之间假定为铰接，且预应力索设置为仅受拉单元；拱脚设置为铰接约束。采用3D3S软件的高级分析模块依照计算长度法的相关规范，进行结构的静力非线性分析和杆件应力比为1.0的满应力设计。为方便施工，实际工程中杆件要采用如下规则进行归并：空间拱桁架上下弦杆要进行截面的分段归并(具体分段点与实际工程一致)，且各榀主桁架弦杆截面方案一致；上下弦杆之间的腹杆要进行左右前后的对称归并(各榀主桁架腹杆方案可不一致)；次桁架弦杆通长一致。采用计算长度法设计完成后，将模型导入NIDA软件中，采用直接分析法计算截面稳定应力比。时程分析时的结构整体初始缺陷的形态采用“恒载+活载”组合下的最低阶整体屈曲模态，如图3所示。除地震作用组合外的各工况组合下的结构整体缺陷模态，采用以下两种模式并分别进行结构稳定性分析，最终计算结果取这两种模式下计算结果的包络值：1)对各工况组合采用各自荷载条件下的最低阶整体屈曲模态或接近整体屈曲的模态；2)对各工况组合均采用“恒载+活载”组合下的最低阶整体屈曲模态。对于杆件初始挠曲缺陷的挠曲方向，采用NIDA软件独有的根据杆件在结构屈曲模态中的空间位移方向自动设置杆件初始挠曲方向的方法；另外，NIDA软件采用改良的力法单元，采用一根杆件对应一个单元的方法，通过引入单元形函数的方法在单元层面上模拟挠曲变形。

图3 变形前结构示意及“恒载+活载”组合下的整体屈曲模态

2.3 分析结果

2.3.1 应力比的比较

根据计算长度法(式(2))和直接分析法(式(9))得到的杆件应力比如图4所示。其中，横坐标为杆件编号，纵坐标为杆件应力比。

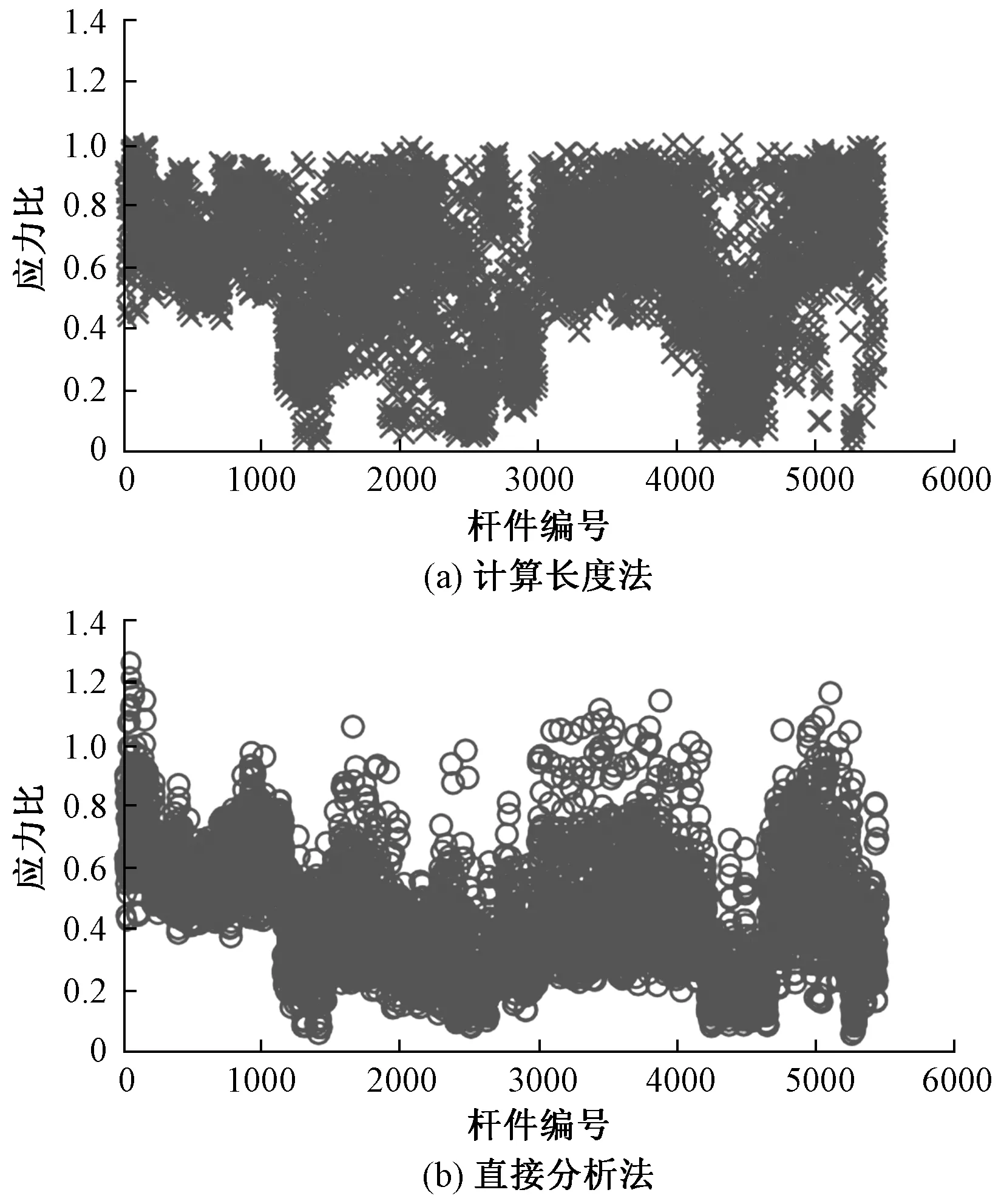
图4 计算长度法与直接分析法的应力比结果

从图4可以看出，同一计算模型采用直接分析法的应力比结果较计算长度法偏小。一方面，由于传统方法的公式中存在计算长度系数，表现出较大的应力比。另一方面，直接分析法虽然应力比偏小，但作为二阶分析方法，杆件截面减小可能会使直接分析法的计算结果突然增大，最终两种计算方法所得到的杆件截面可能相差不大，然而，由于理想杆件的约束条件与实际杆件在结构中的约束条件不一致，计算长度法所采用的计算长度系数通常偏于保守，因此尚存在采用直接分析法对杆件截面进行优化的空间。同时应看到，个别杆件在直接分析法下的应力比超过1.0，这也许是因为结构初始缺陷模态的选择或者杆件初始缺陷的设置方式对计算结果造成的影响，虽不能因此认为计算长度法结果可能存在不安全，但或许可以作为结构校核的辅助参考。

2.3.2 采用直接分析法的截面优化

目前，采用直接分析法时，尚无法实现计算机运算下的杆件自动优化。这是由于采用直接分析法时，要先进行缺陷形态的选定和设置，而现在尚无结构分析计算软件可以实现自动选定及设置功能。且大跨度煤棚结构杆件数量过多，本模型有大约5 000根杆件，若以手动的形式进行直接分析法下的结构优化，则工作量过大。故利用3D3S软件中的杆件自动优化功能，放大截面应力比，以计算长度法进行杆件截面应力比计算并缩小截面，由此计算得到的设计结果再放入NIDA软件中采用直接分析法进行稳定性校核，确认其是否满足规范要求，并可以此作为直接分析法的设计结果。

对于本研究模型，采用计算长度法取应力比1.1进行截面优化，将此时的设计结果导入NIDA软件中采用直接分析法进行验算，直接分析法下的稳定性分析结果如图5所示。其中，有三根杆件的应力比超过2.0，为方便比较，将纵轴最大值设为1.4。

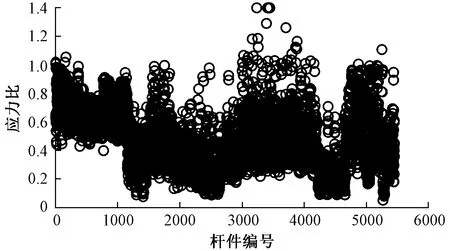
图5 应力比放大后采用直接分析法的验算结果

将图5与图4(b)进行比较后发现，同样采用直接分析法，虽然杆件应力比由1.0放大至1.1，但是大部分杆件截面并未发生变化。原因为：弦杆按照同一个分段规则进行归并，且每一段的截面取最不利杆件的截面；腹杆截面虽可以进行一定的缩小，但限于本工程采用的截面种类较少，可缩小空间也不大。即使如此，仍有部分杆件可进行截面优化。将优化后的模型采用直接分析法校核，大部分杆件应力比可控制在1.0以下。

另外，存在少数杆件的直接分析法应力比超过1.0的情况(30余根)，可采用手动调整截面的方法使其满足设计要求。不满足要求的杆件主要是上下弦之间的腹杆，对这些杆件可直接调整其截面；也存在个别弦杆不满足要求的情况，由于弦杆分段归并以及各桁架弦杆相同的规则，为避免大面积杆件调整而导致的用钢量增加，故对其临近的腹杆进行截面放大，改变其内力分布，使其满足应力比要求。

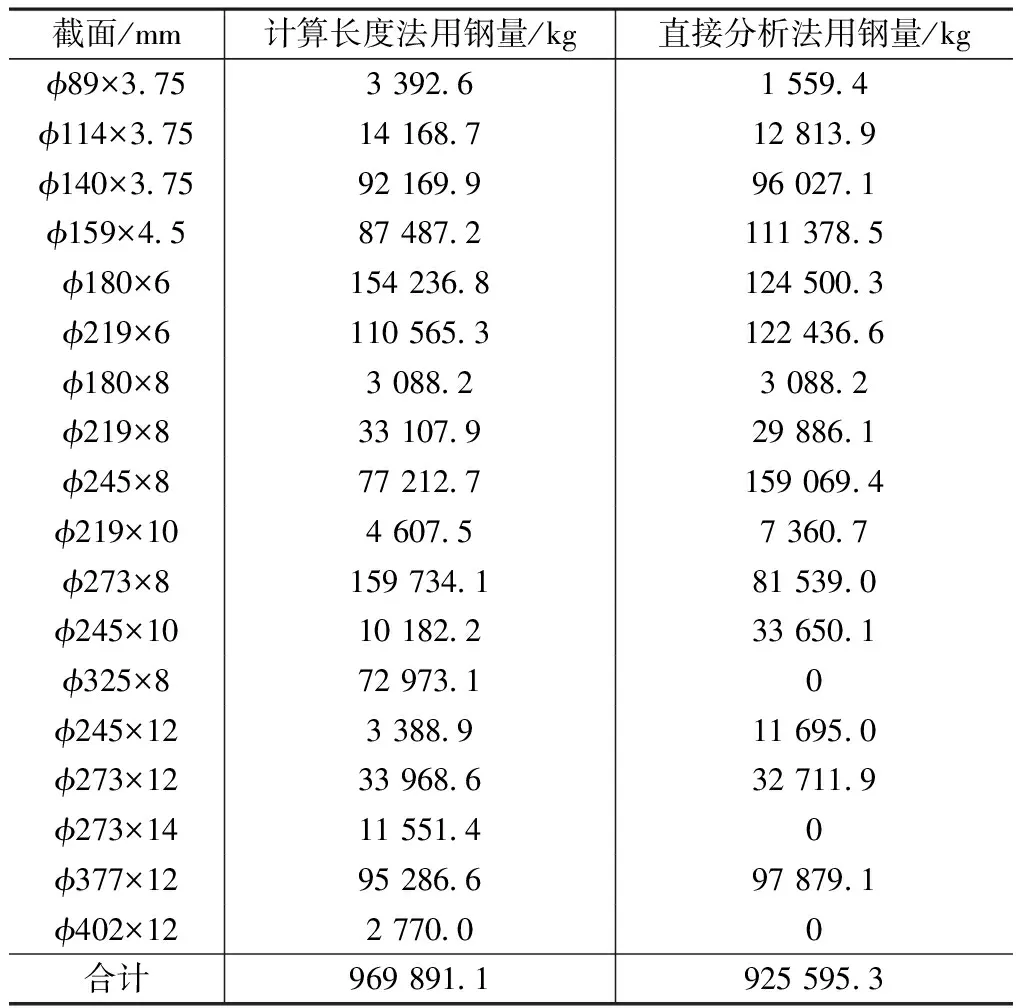
优化后的直接分析法与计算长度法的结构用钢量统计如表2所示。由表可见，本工程若采用直接分析法，用钢量可优化约4.5%。

优化前后的结构用钢量统计 表2

3 结论

本文在阐述钢标中与大跨度空间拱桁架结构设计相关的计算长度法和直接分析法的稳定性分析设计规定的基础上，以某含预应力索的155m跨度空间拱桁架煤棚设计工程为例，对比了计算长度法与直接分析法的设计结果，得到以下结论：

(1)对于含预应力索的大跨度空间拱桁架结构，在计算长度法设计的基础上可采用直接分析法对杆件进行进一步优化。

(2)大跨度空间网格结构杆件数量过多，直接采用直接分析法进行优化工作量太大且不易进行。可采用计算长度法将应力比放大一定程度后，采用直接分析法校核调整。本工程对于计算长度法应力比1.0的情况，将其放大至1.1并进行截面优化，再进行直接分析法下的截面校核调整，可满足设计要求。本工程采用直接分析法可使用钢量优化约4.5%。

本文中，对于腹杆两端的连接条件假定为刚接。按照钢标的5.1.5条第3款之规定，细长的桁架腹杆可视为两端铰接进行设计。通常出于安全考虑，可取腹杆两端刚接和两端铰接两种假定下的设计结果的包络值。对于腹杆两端铰接假定下直接分析法与计算长度法的比较将在今后进行研究。