基于太赫兹波段的三反变焦系统设计

杨旭，牟达，陈炳旭，蒋锐，程爽

（长春理工大学 光电工程学院，长春 130022）

空间遥感是飞行高度在80 km以上的大气层之外对地进行观测的技术［1］，微波和红外遥感技术目前在这个领域相对成熟。而宇宙背景辐射约有50%都集中在太赫兹波段，同红外波段相比，太赫兹具有穿透本领强，可穿透尘、雾等障碍，探测本领更强的特点；与微波波段相比，太赫兹波长较短，能够得到更好的空间分辨率和允许更小尺寸的光学组件［2-3］。因此，随着人们对空间遥感探测分辨力的要求越来越高，开展在太赫兹波段的空间遥感探测工作具有重要的意义。

20世纪80年代，第一代多光谱反射变焦望远镜由波音公司开发［4］。在空间探测领域中，与折射光学系统相比，反射光学系统具有如下优点：系统重量轻、光能透过效率高、热稳定性良好、无色差，多光谱成像等优点［5］。因此，反射系统的设计受到了更多的关注。反射系统的专利也相继问世［6-7］。反射变焦系统通过大视场进行搜索目标，小视场对目标进行定位，在空间遥感卫星探测领域得到了广泛的应用。

本文首先基于三级像差理论设计了一款太赫兹波段的共轴三反变焦系统。然而该方法只能提供部分结构参数，具有一定的局限性。同时由于共轴系统存在遮拦，随着视场的进一步增加，共轴反射变焦系统无法满足其成像质量。为解决这一问题，本文基于矢量像差理论设计了一款太赫兹波段的无遮拦反射变焦光学系统。与存在中心遮拦的共轴反射变焦光学系统相比，无遮拦反射变焦系统更具有应用价值。

1 设计原理

1.1 三反变焦系统的三级像差理论

传统变焦光学系统按照光学元件移动方式的不同分为机械补偿式变焦和光学补偿式变焦，大多数变焦光学系统使用机械补偿式变焦形式，与光学变焦相比，变焦过程相对简单，可获得较大的变倍比［8］。传统的机械补偿式变焦是由有运动光学元件的组元组成的，在变焦过程中，变倍组轨迹是线性的，补偿组轨迹是非线性的。在三反变焦系统中，变倍组为次镜，补偿组为三镜，二者的共轭距之和是一个常数［9］。

式中，k表示光学系统具有k个位置；β2i，β3i为系统在第i个位置时的次镜与三镜的垂轴放大率。为与式（1）、式（2）表述一致，对三级像差理论进行推导的过程中，可以选择，β2i，β3i作为自变量。具体的过程如下：

（1）各个镜子之间的间隔表示为：

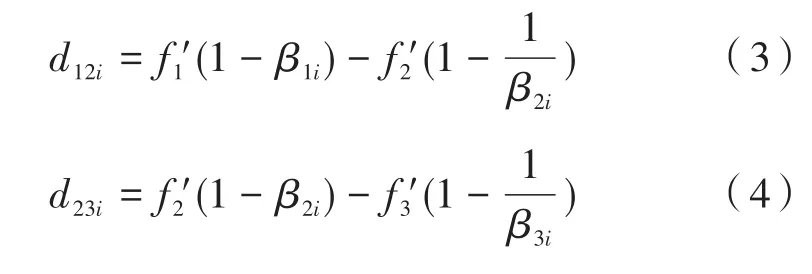
（2）分别对辅助光线进行逐面的傍轴追迹［10］，获得在各个面上的投射高度、入射角和出射角等高斯参数的解析表达式；

（3）在已解得的高斯参数的基础上，求解出不同焦距时各反射面的像差特性参数P，W［11］；

（4）根据初级像差的定义与性质，通过各反射面像差特性参数P，W与光学系统共轭距之间的数学关系，最终推导系统在不同焦距值下，由，β2i，β3i表示的各三级像差系数的表达式：

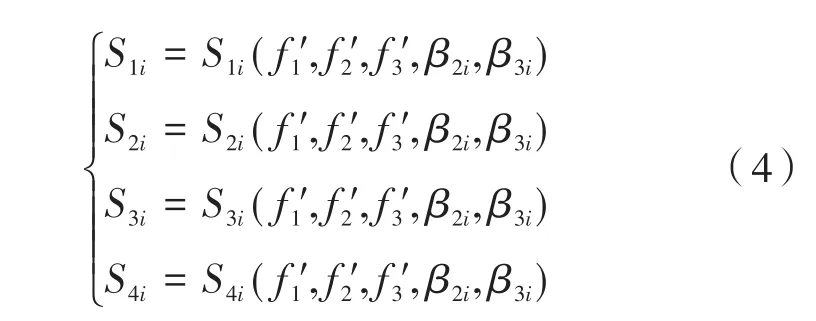
此时，各个位置的焦距可以表示为[8]：

1.2 无遮拦三反变焦系统

因为共轴反射系统存在中心遮拦，如何进一步增大共轴反射变焦系统的视场，并满足成像要求成为一个问题。为了解决这一问题，需要将系统无遮拦设计，来消除系统中心遮拦，对于无遮拦反射变焦光学系统设计的重要理论依据是矢量像差理论[12]，其关键在于如何确定反射系统中各个镜子的偏心与倾斜量。

偏心与倾斜系统中的彗差可以表示为：

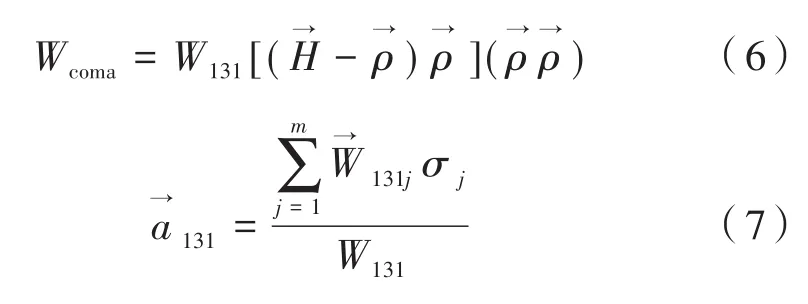
偏心与倾斜系统中的像散可以表示为：

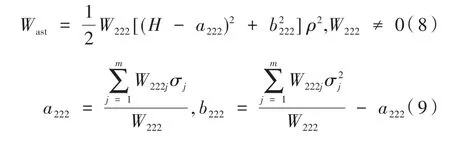
在偏心与倾斜系统中，像散中点在像面上的位置由矢量H=a222±ib222决定。通过对上述公式的研究可以得知，在无遮拦系统中，彗差的中心并不是像面的中心，像散的零点存在两个零值点，如图1所示。与此同时，在偏心与倾斜系统中，失调量δj是关于等效倾斜量βj的函数，函数关系可表示为：

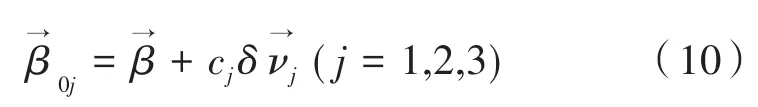
其中，cj表示各个镜子的曲率半径；βj表示各个镜子的倾斜量；δνj表示各个镜子的偏心量。

由于变焦系统中各个参量的变化，a131p和(a222±ib222)p分别为变焦系统在第p个位置时彗差和像散的中心。为了使波前差最小，系统在变焦过程中，彗差的中心与像散两个零点连线中心重合，可以通过计算各镜的倾斜与偏心量来实现，如图2所示。进行无遮拦反射变焦系统设计的关键在于如何确定各个镜子的偏心量和倾斜量。通过讨论彗差与像散两者之间的数学关系，系统各镜的倾斜与偏心量由公式（11）求解。

图1 彗差的中心和像散的两个零点

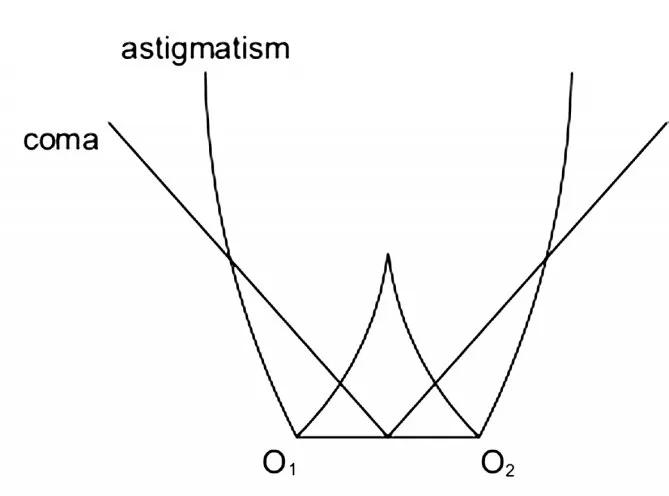
图2 彗差和像散的校正

2 设计实例

基于三级像差理论与矢量像差理论，结合空间遥感探测系统的设计指标要求，设计一款宽谱段、高分辨率大变倍比的太赫兹三反变焦距光学系统。设计指标如表1所示。

在计算初设结构时，先选取300 mm，600 mm，1 200 mm三个焦点位置，代入公式（3）中，并对这三个位置的初始像差进行校正；同时为达到机械补偿变焦的条件，系统须满足公式（1）要求。满足如下方程组：

表1 共轴三反变焦系统设计参数

考虑系统设计的实际应用性，使求解的结构具有意义，加以如下约束条件：

由于公式（12）的方程个数大于未知数，所以存在一系列解系。使用最小二乘法的方法进行优化，并得出最优解。计算出来的初始结构只能满足基本几何尺寸要求，无法满足成像要求。通过光学软件CODEV光学设计自动程序进行进一步优化。在初始结构优化的过程中，将各个镜子的曲率半径与相邻两个镜子之间的距离都设置为变量。为平衡系统的高级像差，将反射面面形设置为非球面，考虑到反射镜加工的实际问题，将非球面系数设置为8次。优化后的结构图和各个焦距下10 lp/mm处的调制函数（MTF）分别如图3和图4所示。该系统布局简单、成像质量良好。在变焦过程中系统的次镜作为变倍组，三镜作为补偿组，在各个变焦节点处均满足设计要求。

但由于共轴系统的孔径存在中心遮拦，有效通光孔径会减小。而光学的调制传递函数（MTF）受限于光学系统F数、工作波长和有效通光口径，中心遮拦会限制共轴系统的MTF，每个焦距处在10 lp/mm处仅能达到0.2。表2为光学系统在奈奎斯特频率处MTF值与遮拦比的关系，其中遮拦比定义为遮拦口径D遮拦与光学系统入瞳口径D0的比值：D遮拦D0。通过对各个焦距的MTF的分析，可知该共轴反射变焦系统的遮拦比为0.45。为了在奈奎斯特频率处有较高的MTF值，应对系统遮拦进行有效控制。

图3 共轴反射变焦系统结构图

图4 共轴反射变焦系统在各个焦距值下的MTF值

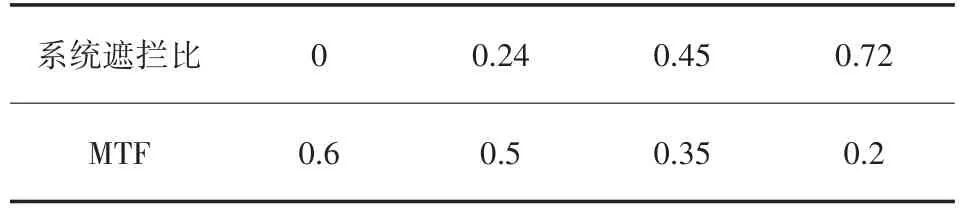
表2 系统遮拦比与MTF的关系

由于共轴反射系统存在中心遮拦，系统视场无法进一步变大；为解决这一问题，使用无遮拦反射变焦光学系统替代共轴反射变焦系统。该系统的设计参数如表3所示。

太赫兹波段的无遮拦三反焦光学系统在同样变倍比的要求下，依然是次镜作为变倍组，三镜作为补偿组；视场从共轴系统的线视场扩大到为面视场，同时缩短了系统的轴向尺寸，满足轻量化设计、高分辨成像设计需求。系统优化后的结构图如图5所示。系统在各个变焦节点处均满足空间频率10 lp/mm时，MTF≥0.3，满足系统的成像质量要求，如图6所示。

3 结论

首先，将太赫兹波段分别与红外波段和微波波段作比较可以得知，太赫兹波段以其独特的性质在空间遥感探测中发挥着重要作用。其次，根据空间遥感探测光学系统的技术要求，基于三级像差理论，通过数学关系的推导，建立了三级像差系数和系统各个反射镜的焦距以及垂轴放大率之间的关系式。再加入适当的约束条件以后，并通过最小二乘法得到系统的初始结构，设计出一款太赫兹波段的共轴三反变焦光学系统，验证了三级像差理论的可行性。但是对于共轴反射变焦光学系统而言，由于系统存在中心遮拦，当视场进一步增大时，进入光学系统的能量急剧下降，无法满足其成像要求。为了解决这一问题，应用矢量像差理论计算出符合要求的无遮拦反射变焦系统。求解系统中各元件的倾斜与偏心量，使得彗差零点与像散中心重合，获得光学系统的初始结构，通过软件优化后，设计出一款太赫兹波段无遮拦三反变焦光学系统。最后将两个设计结果相比较，无遮拦反射变焦光学系统相对于共轴反射变焦光学系统，可得到更大的视场角，其光学性能更好，可获得的信息更多，更适合应用在空间遥感探测领域。

表3 无遮拦三反变焦系统设计参数

图5 无遮拦反射变焦系统结构图

图6 无遮拦反射变焦系统在各个焦距值下的MTF