基于机器视觉的金属板材表面波纹度检测方法

周神特,张 潇,王宇宇,柯 宇,赵文宏

(浙江工业大学 机械工程学院，杭州 310014)

经过砂带平面磨床加工后的金属板材主要是去除了板材表面的锈蚀、表面瑕疵、电镀层和氧化皮等表面覆盖物，随着制造业的发展，对金属板材表面质量的要求日益提高[1-2]。表面质量的一个重要评判标准就是表面波纹度，表面波纹度是介于表面粗糙度和表面形状误差之间的表面几何不平度，表面波纹度影响着金属板材的抗疲劳强度、抗腐蚀性、磨损性能以及外观等[3]。

目前，常规金属板材表面波纹度的检测方法大都采用接触式检测，该方法在一定程度上会对金属板材造成一定的损伤，且检测效率低、精度不高。基于机器视觉的金属板材表面波纹度检测方法是一种非接触式的方法，该方法能够快速、有效地提取表面信息，实现无损检测，有效地提高金属板材的检测速度，降低误检率[4]。

HORN[5]通过研究图像表面的成像机理和光线反射原理，提出了明暗成形的原理，通过分析拍摄的单一表面图像来获取形貌轮廓。WOODHAM[6]等基于Lambert定律提出了一种光度立体测量法，用于提取表面轮廓形貌。ZHANG[7]提出了一种利用投影产生光栅图像的测量光学结构，以此获得标准工件表面的波纹度轮廓和波幅。

目前,国内外基于机器视觉的波纹度检测大多数集中在对木材表面的研究，对金属材料表面的研究较少，仅有的一些研究理论仅限于小尺寸零件表面波纹度的测量，并且这些测量方式存在较大限制，一般只适合于实验室的精密研究，不适宜用于生产环境中金属板材波纹度的测量[8]。因此，基于机器视觉的高效、高精度的金属板材表面波纹度测量方法具有重要意义。

1 表面波纹度评定参数

表面波纹度的主要评定参数均定义在波纹度轮廓的一个取样长度范围内，工程应用较多的评定参数为波纹度的轮廓算术平均偏差参数Wa[9]。波纹度轮廓中波峰和波谷的变化信息如图1所示，该参数反映了波纹度轮廓中波峰和波谷的微小变化等重要信息。因此，采用Wa作为金属板材表面波纹度的评定参数。

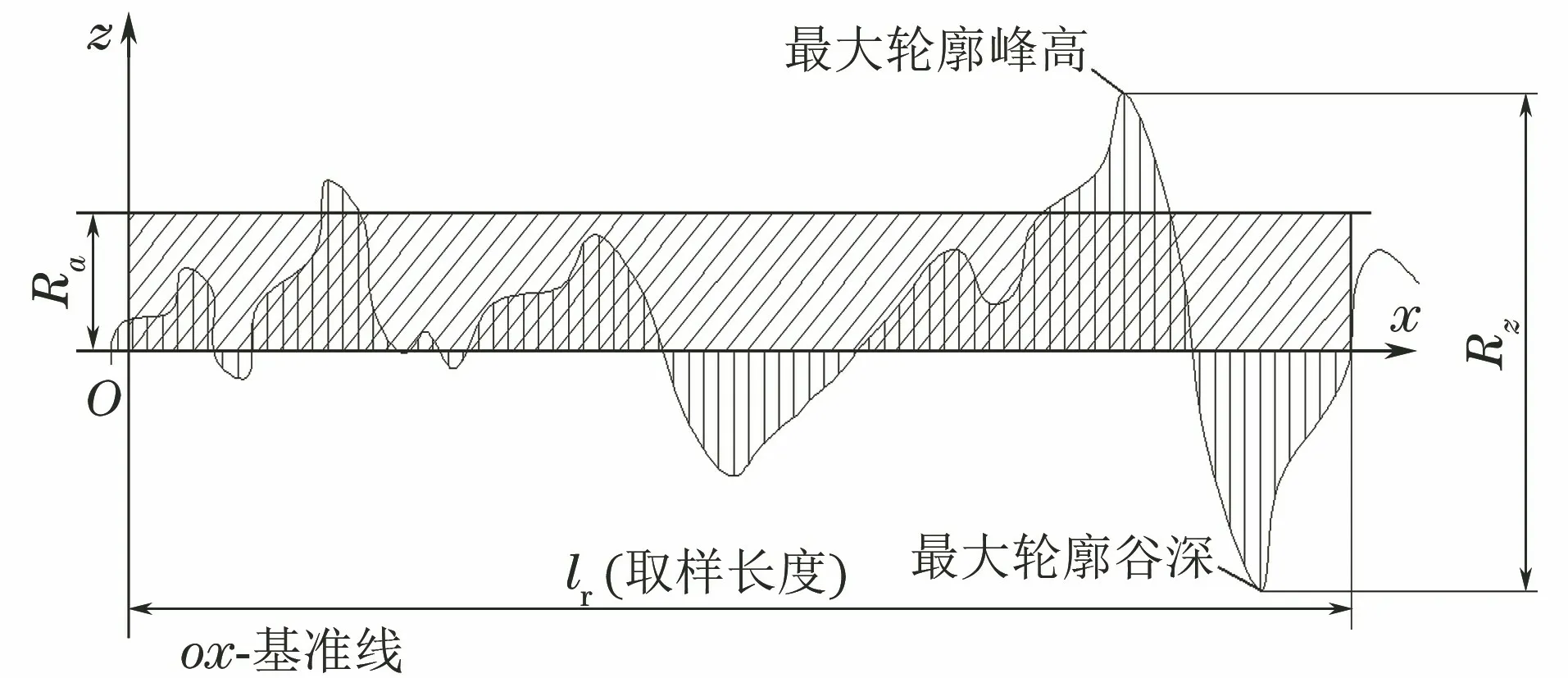
图1 波纹度轮廓中波峰和波谷的变化信息

通过工业相机与特定光源所采集到的金属板材图像能够较好地反映出表面波纹度的特性[10]。将这些图像进行对比后发现，在光照和环境条件一致的情况下，相同波纹度的等级试样，其表面图像纹理特征呈高度的统一性，而不同波纹度等级试样的表面图像纹理特征呈明显的差异性。因此，可通过提取表面图像纹理的特征信息，建立与表面波纹度之间的关系模型，来实现对工件表面波纹度的测量。

2 金属板材表面的纹理特征提取

图像中噪声的灰度值与邻域内的像素点灰度值相差较大[11]。中值滤波可以克服最小均方滤波、平滑滤波等线性滤波器所导致的图像细节模糊问题，是滤除脉冲干扰和图像扫描噪声最有效的方法。但是中值滤波耗时较长，去除噪声的性能受到模板窗口的限制。根据金属板材表面图像的灰度分布特点，可以在求取滤波时考虑移动的两列像素的灰度值变化，对中值滤波去噪算法进行加权加速。加权快速中值滤波去噪前后的金属板材表面纹理特征如图2所示。

图2 加权快速中值滤波去噪前后的金属板材表面纹理特征

改进后的中值滤波算法减少了中值滤波的计算量，在去噪的同时较好地保证了图像的纹理特征，保证了检测的快速性和实时性。

图像的纹理特征参数与方向具有一定的相关性，为了加快相关参数的提取和分析，需要将图像旋转至与纹理方向一致。基于图像的全局特征，选择具有特定形状特征的边缘像素，并连接成连续平滑边缘的过程称为霍夫变换。在参数空间中找到相交线最多的一点并确定该点的参数，就能确定图像空间中的某一特定直线的方程，达到直线检测的目的[12]。

建立平面极坐标系的原因是有些直线斜率为0，直线的极坐标如式(1)所示。

ρ=xcosθ+ysinθ

(1)

式中:ρ为直线距原点的法线距离；θ为直线与x轴的夹角。

霍夫变换的计算步骤如下所述。

(1) 首先进行图像二值化处理，待检测区域为灰度值为“1”的像素点。

(2) 在极坐标空间里建立一个累加列表A(ρ，θ)，初始值为0。

(3) 对于感兴趣区域，遍历θ，对应的数组A(ρ，θ)累加，直到所有灰度值为“1”的像素点全部遍历完成。

(4)累加结束之后，数组A中最大值对应的参数就是要检测的直线的参数。

经过霍夫变换计算的其中一条直线如图3所示，直线为经过霍夫变换计算的其中一条，根据找到的直线，即可获得旋转角度。

图3 经过霍夫变换计算的其中一条直线

图像旋转公式如式(2),(3)所示。

(2)

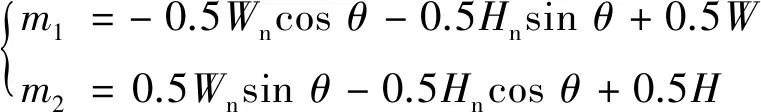
(3)

式中：m1,m2为旋转参数;W为原始图像宽度;H为原始图像高度;Wn为输出图像宽度;Hn为输出图像高度。

图4为基于霍夫变换的图像旋转结果。

图4 基于霍夫变换的图像旋转结果

灰度共生矩阵通过计算像素点灰度值的排列位置关系及分布密度关系来反映图像空间的灰度关系，是反映图像纹理特征的重要分析方法。对灰度共生矩阵各元素值的分析可反映图像灰度在相邻方向、间隔、变化幅度等方面的综合信息，即图像整体分布特征，同时也可描述灰度等级相同图像的像素点密度[13]。灰度共生矩阵的数学表达式为：

P(i,j,d,θ)={[(x,y),(x+Dx,y+Dv)]|

f(x,y)=i,f(x+Dx,y+Dv)=j}

(4)

式中:x，y为图像中像素的坐标；d为生成步长，是大于0且小于图像分辨率最小值的整数；θ为生成方向，一般取0°,45°,90°,135°等4个方向。

首先,将每幅图像的灰度级量化，选择像素点偏移距离和角度。灰度共生矩阵由图像的灰度级、生成步长以及生成方向共同决定。因此，针对不同位置的金属板材图像，需要选取适当的结构参数以获得具有最大表征能力的纹理特征的统计特征参数。

(1) 图像灰度级的确定

对图像的灰度级进行压缩归一化处理，归一化的公式为

F(x,y)=INT[f(x,y)×L/fM]+1

(5)

式中：L为归一化后灰度图像最大的灰度级；fM为原灰度图像中灰度的最大值。

为了减少计算量，使数据离散性较好，将图像压缩至16的灰度级。

(2) 生成方向的确定

选取和纹理方向一致的90°方向来生成灰度共生矩阵，可以保证纹理特征统计参数提取的有效性，同时减少计算量，加快处理速度。

(3) 生成步长的确定

图像在压缩的过程中，图像中的一些像素点将不能参与到灰度共生矩阵的生成中，使一些重要的纹理信息弱化或者消失，图像的真实信息无法得到准确反映。在灰度级压缩至较小范围的情况下，通常选取d=1的生成步长，才能够最大限度地反映图像的纹理信息。

特征参数与对应的表面波纹度实际值之间的相关程度较高，使用皮尔逊相关系数来描述波纹度与参数之间的相关性。皮尔逊相关系数是反映两个变量相关程度的统计指标，表达式如式(6)所示。

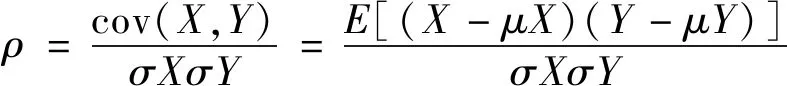
(6)

式中：cov(X,Y)为两个变量的协方差;sX,sY为X,Y的标准差；E为期望。

根据拍摄的金属板材粗糙度样块的表面图像，提取10个基于灰度共生矩阵的特征参数，分别计算出各个特征参数与波纹度之间的相关系数和波动系数，特征参数的表征能力分析如表1所示。

表1 特征参数的表征能力分析

分析表1可以发现，根据灰度共生矩阵选取的10个特征参数与波纹度之间存在一定的相关性，其中能量、反差、相关、逆差距和熵等5个参数与波纹度具有较高的相关系数，而另外5个特征参数的表征能力置信度低于0.7，表征波纹度这种高精度的数据需要采用较高置信度的特征参数，在相关系数较高的5个特征参数中，可以发现，逆差距的波动系数小，稳定性不够高。综上所述，选取能量、反差、相关和熵这4个特征参数，能稳定、高效地表达波纹度，基于这些参数，建立了金属板材表面波纹度的检测模型和特征体系。

3 模型建立与试验结果分析

BP(Back-Propagation)神经网络是神经网络中使用最为广泛的一类，其将系统所产生的误差返回到输出值，利用误差来调整神经元的权重，生成一个可以模拟出原始问题的人工神经网络系统[14]。反向传播的基本思想就是通过计算输出层与期望值之间的误差来调整网络参数，从而使得误差变小。BP神经网络模型中有3层结构，输入层、隐藏层和输出层，其误差计算公式如式(7),(8)所示。

δ[L]=αL⊙σ′(z[L])

(7)

δ[ι]=ω[l+1]Tδ[l+1]⊙σ′(z[l])

(8)

式中:δ[L]为输出层误差;δ[ι]为隐含层误差;a为学习率;T为输出。

参数变化率如式(9),(10)所示。

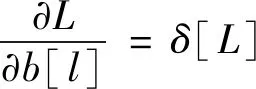
(9)

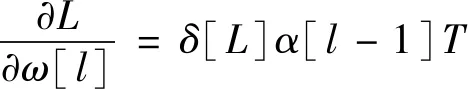
(10)

式中：b为偏置项。

参数更新是BP神经网络最重要的一个环节，直接影响模型预测准确率。式(11)，(12)为参数更新的过程简化。

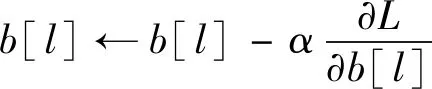
(11)

(12)

输入层神经元的数目过少，表征能力不足，映射关系的建立将存在一定难度。由上文可以得到，基于灰度共生矩阵提取的对比度、相关、能量、熵这4个特征参数对波纹度值具有较强的表征能力，因此，选取这4个参数作为输入，则输入层的神经元数目可以设置为4[15]。以表面波纹度为检测对象，输出层为波纹度值。模型输出相对误差Error、均方误差MSE数学表达式如式(13),(14)所示。

Error=|bij-aij|max

(13)

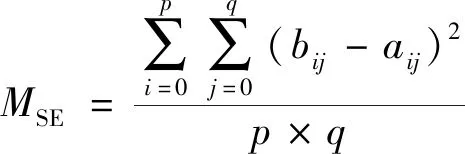
(14)

式中：aij为神经网络实际输出矩阵中的元素;bij为神经网络期望输出矩阵中的元素。

由表2可知，当隐含层神经元数目为4，6，8，10时，均方误差、不同神经元数目的相差不大，训练时间在隐含层神经元个数为6时最短。综合考虑相对误差以及训练时间的大小，选择隐含层神经元数为6。设定BP神经网络的参数如表3所示。

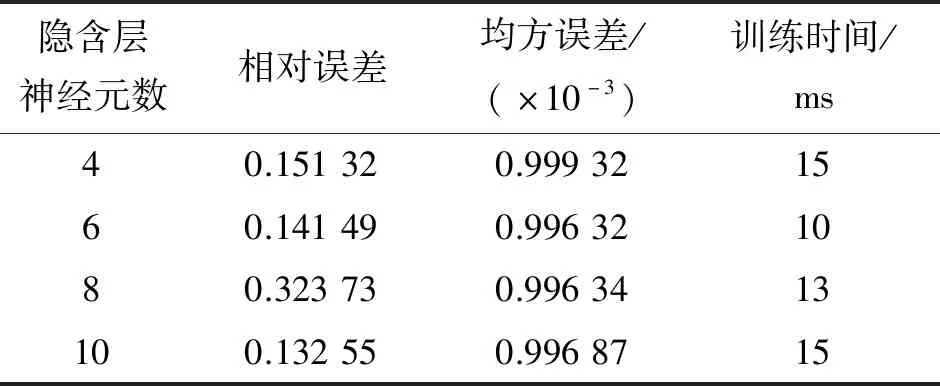
表2 不同隐含层神经元数目下的神经网络性能

表3 BP神经网络参数

金属板材表面波纹度一般要求小于0.8 μm，选取波纹度值分别为0.35，0.55，0.75,0.95 μm的金属板材样块。这些样块用表面轮廓测量仪进行测量，对同一样块的不同位置分别进行3次测量，同时计算出相应的特征参数。

根据图像基于灰度共生矩阵的统计特征参数，输入模型中进行训练，训练样本如表4所示，将检测结果与表面轮廓仪的实际测量值进行对比，结果如表5所示。

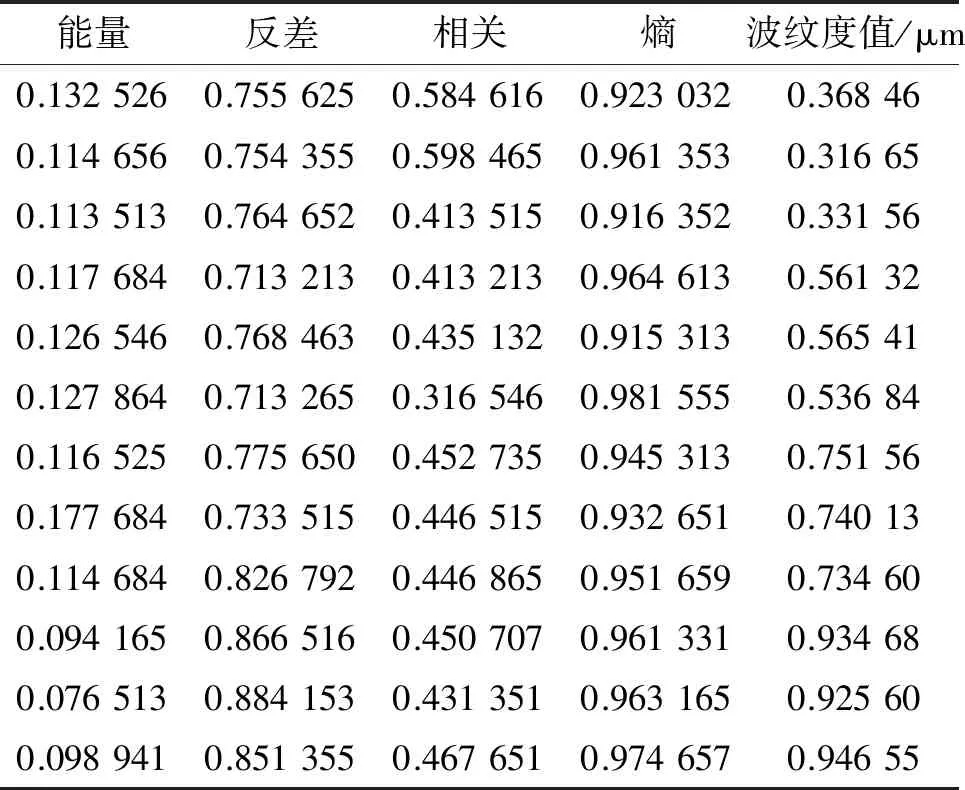
表4 训练样本

波纹度检测模型的训练样本来源于尺寸较小的金属板材试样，拍摄的尺寸、图像的放大倍率、光照的均匀性、试验环境的干扰等都会对预测精度造成一定的影响。由表5可知，增加大尺寸金属板材的样本训练后的波纹度检测模型，检测结果与实测值的最大绝对误差值仅为0.051 μm，相对误差平均值仅为4.90%，准确率达95.10%，达到了对金属板材表面波纹度的检测要求，证明了表面波纹度检测模型在大尺寸金属板材表面波纹度检测中的可行性。

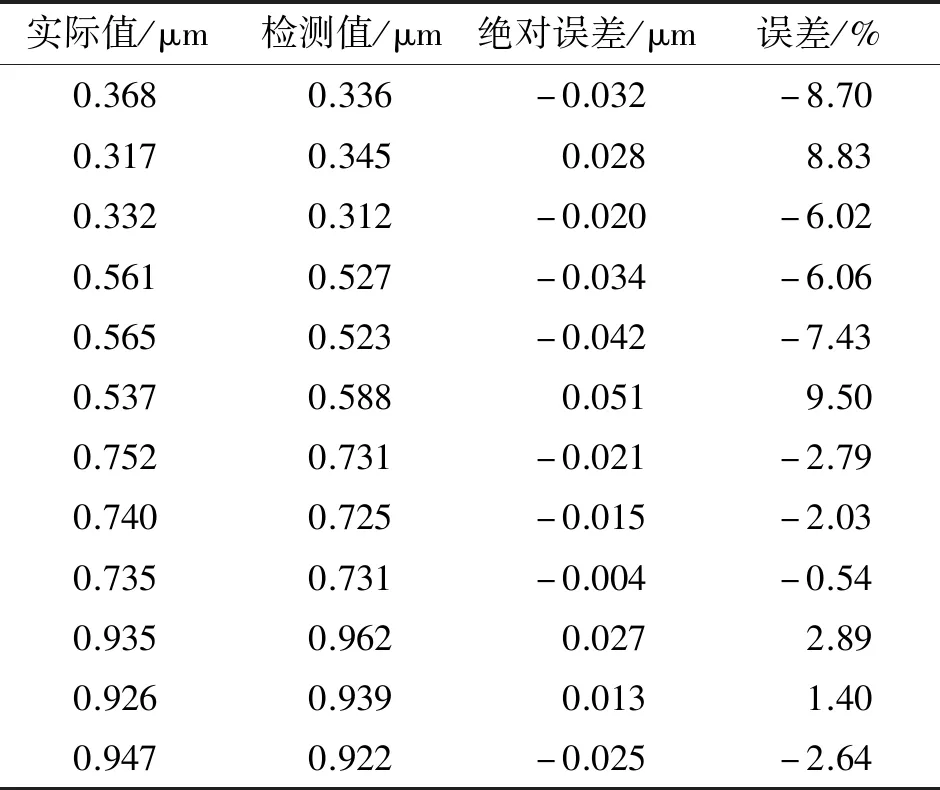
表5 实际值与检测值对比

4 结语

针对金属板材的表面特性，提出了一种非接触式的无损检测表面波纹度检测方法。该方法首先通过加权快速中值滤波实现图像去噪，利用这种去噪方法有效地提升了图像的去噪效率，之后提取图像基于灰度共生矩阵的特征参数，验证了与波纹度的相关性，并选取置信度较高、较为稳定的特征参数，最后将特征参数作为输入参数，构建了基于BP神经网络的表面波纹度检测模型，并将检测值与表面轮廓仪测量值进行对比，检测结果与实测值误差在允许范围内，试验检测误差仅为4.90%，验证了该检测模型的可行性，能够实现金属板材表面波纹度的快速、高精度检测。