有关Janowski 型凸象函数的调和函数积分表达式和系数不等式

张晓丽，李书海

(赤峰学院数学与计算机科学学院，内蒙古赤峰 024000)

1 引言

设A表示在单位圆盘内解析且具有形式

的函数f(z) 全体.

设u(z) 和v(z) 是D内解析函数，若存在D内解析函数使得u(z)＝v(ω(z)) ，则称u(z) 从属于v(z) ，记为u(z) ≺v(z)[1].

设A，B∈ ℜ， -1 ≤B ＜ A ≤1 ，若函数在D内解析且满足条件

则称p(z)∈P(A，B)[2].显然P(1 ， -1)＝P是正实部函数.若p(z)∈P(A，B)，则[3]

用SH表示在圆盘D内满足条件f(0)＝fz(0)-1＝0 的复值单叶保向调和函数且具有形式

的f(z) 组成的函数类，其中解析部分h(z) 和共轭部分g(z) 均为D内解析函数，并具有下列幂级数表示[5]

Mocanu 在文献[6 -8]中引进并研究调和函数类M性质.文献[9]中推广M，研究函数类:

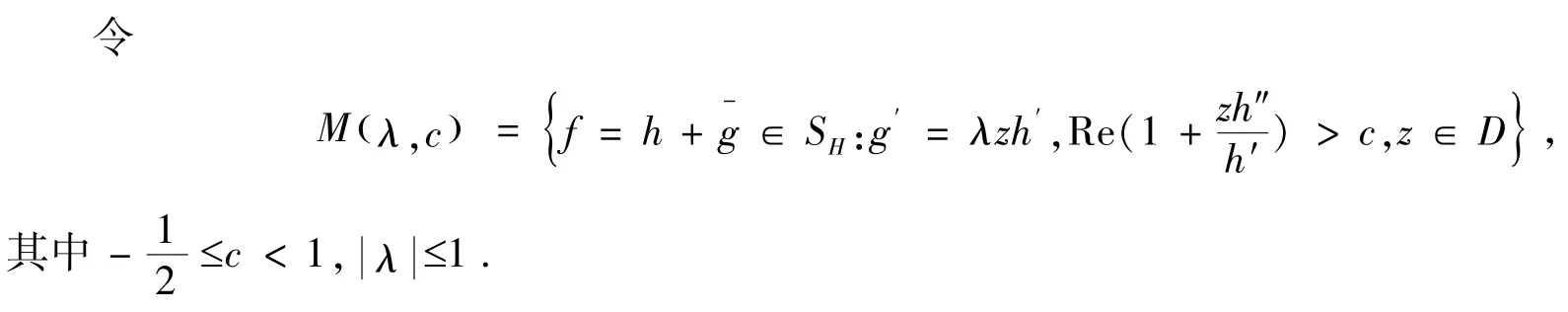
孙勇等在文献[10]中引进函数类M(λ，c)，进一步推广M，得到重要结果.

那么能否用Janowski 型凸象函数定义h(z) ，从而进一步推广函数类M? 有关这个问题没有发现相关文献，是有待进一步研究的问题.本文重点讨论以上两个问题.

2 预备知识

引进如下调和函数类Hλ(A，B) :

显然Hλ(A，B) ⊂M(λ，c)⊂Q(D) ⊂M.

我们需要如下引理:

引理1[11]解析函数h定义在D上，h是近于凸的充分必要条件为h′(z)≠0 ，且满足

其中θ1＜θ2＜θ1+2π，0＜r ＜1 .

引理2[12]若调和函数对于所有解析函数h + ηg都是近于凸的，则f也是近于凸的.

引理 3设A，B∈ ℜ， -1 ≤B ＜ A ≤1 ，函数h(z)∈K(A，B) 当且仅当存在D内解析函数w(z) :w(0)使得

证明：先证必要性.设函数h(z)∈K(A，B) ，则

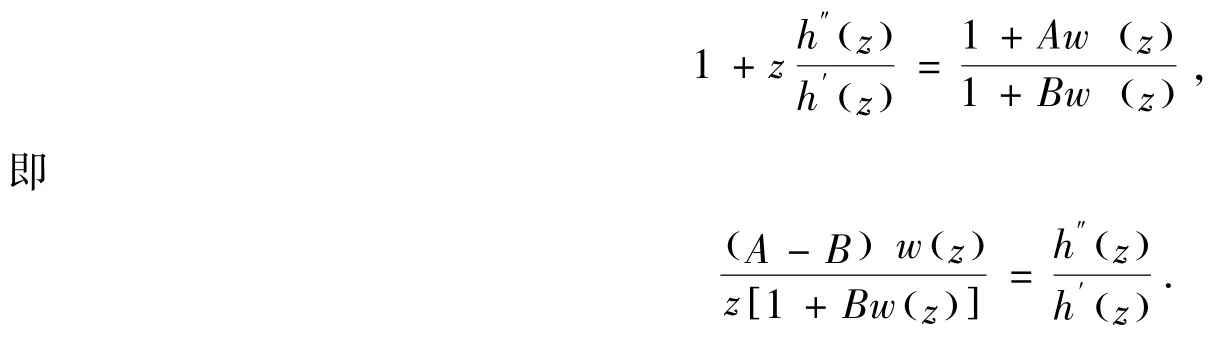
上式两边同时积分两次，得到

接下来，证明充分性.设(2.1)式成立. 即存在D内解析函数使得

即h(z)∈K(A，B) .证毕.

本文中，我们将利用解析函数h(z) 的性质，结合h(z) 和g(z) 的关系，讨论类中调和函数的积分表达式和系数不等式，解决了文献[9]中相应的问题，同时推广了文献[10]中的相关结果.

3 主要结果

首先， 求类中函数的积分表达式:

定理1若则存在D内解析函数使得

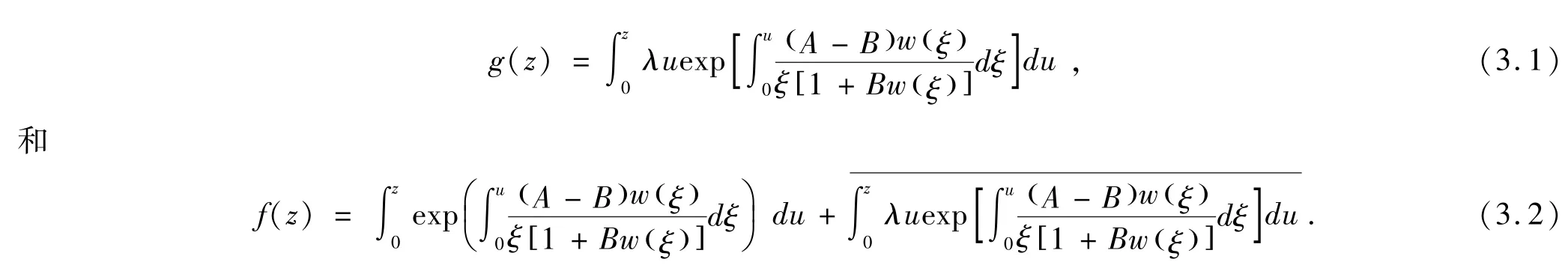
证明若根据引理3，存在D内解析函数使得

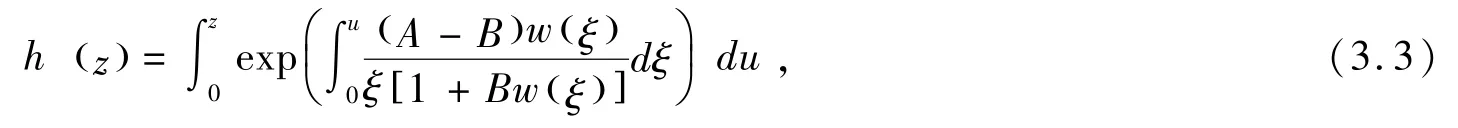
并结合g′(z)＝λzh′(z) ，推出

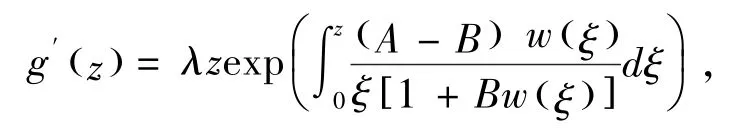
上式两边同时积分，得

由(3.3)和(3.4)即得(3.2)式成立.证毕.

下面证明类中函数的单叶性:

定理2设f ＝h + g-∈Hλ(A，B)，则f(z)是单叶近于凸函数.

证明令F(z)＝h(z)- ηg(z)，其中则

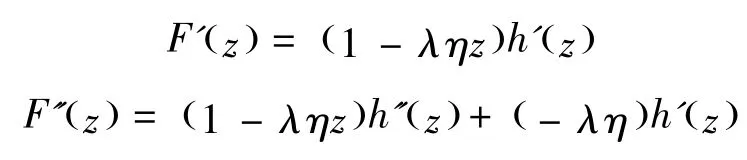
显然F'(z)≠0，z∈D.则利用上式，我们有

所以，依据引理1 可知F(z)＝h(z)-ηg(z)是近于凸的，由于根据引理2，f(z)是单叶近于凸函数.证毕.

下面讨论系数估计:

定理3设则有系数估计

注当时，从引理3、定理2 -定理4 分别得到文献[9]中定理1 -定理4 对应的结果；同时A ＝1-2β(0 ≤β ＜1)，B ＝-1 时定理3 局部推广了文献[10]中的定理1.

4 结论