两种降低复杂度的符号翻转多元LDPC译码算法

陈海强 王瑶玲 韦文娟 蒋炳旭 孙友明 黎相成 覃团发

(广西大学计算机与电子信息学院 南宁 530004)

(广西多媒体通信与网络技术重点实验室 南宁 530004)

1 引言

与2元低密度奇偶校验码(Low Density Parity Check code, LDPC)相比较，构建在 q阶有限域上的多元LDPC码[1]具有更加优秀的译码性能，特别在码长较短、码率较大时，其优势更加明显。然而，多元LDPC码的性能增益往往是以高译码复杂度作为代价换取的。降低多元LDPC译码复杂度的主要思路是降低Tanner图上参与运算的节点数量以及每个节点的运算操作。经典的降低复杂度的多元LDPC译码算法包括基于概率域的和积(Q-ary Sum Product Algorithm, QSPA)算法[2,3]以及基于扩展最小和(Extended Min-Sum, EMS)的译码算法[4]及其改进版本[5-8]。此外，基于大数逻辑(Majority-LoGic Decoding, MLGD)的简化译码算法[9-12]，也能达到降低译码复杂度的目的。

基于符号翻转的译码算法(Symbol Flipping Decoding, SFD)是另一类重要的简化译码算法，能在性能和复杂度之间进行有效的折中。最初的SFD算法是文献[13]提出的广义Gallager算法B(Gallager’s Algorithm B, AlgB)及其改进版算法(weighted-Algorithm B, wtd-AlgB)。AlgB算法具有很低的译码复杂度，但性能较差；wtd-AlgB算法结合了汉明距离和多数逻辑(plurality-logic)准则，获得一定的性能增益。其他传统的SFD算法还包括文献[14]的并行符号翻转算法(Parallel Symbol Flipping Decoding algorithm, PSFD)以及基于投票机制的符号翻转算法[15,16]等。2017年，Wang等人[17]提出了基于距离和预测机制的符号翻转(Distance-Symbol Flipping Decoding with Prediction, D-SFDP)算法，与传统的SFD算法不一样，D-SFDP算法不仅考虑了符号翻转之前的信息，还把翻转后引起的目标函数变化考虑进来，以此预测和翻转迭代过程中的硬判决符号。与非预测的符号翻转算法相比，D-SFDP算法能获得明显的性能提升。2018年，Mu等人[18]提出了一种基于迭代停止准则的加权符号翻转译码算法，提高了译码算法的收敛速度。2019年，Dai等人[19]对D-SFDP算法进行了改进，修正了算法的本地循环震荡问题，Oh等人[20]提出了一种基于判决符号可靠性的符号翻转译码算法。

虽然D-SFDP算法具有优秀的译码性能，但仍是以牺牲一定的复杂度换来的。特别地，由于D-SFDP算法每次只能翻转1个符号，这导致其平均迭代次数远远高于其他同类算法。因此，降低该算法每次迭代的复杂度很有必要。本文首先提出一种基于加性参数的改进型wtd-AlgB算法，通过调整距离参数避免了乘性操作，从而降低复杂度；其次，本文提出一种基于截断型的预测机制符号翻转译码算法(Truncation-based Distance-Symbol-Flipping-Decoding with Prediction, TD-SFDP)，结合翻转函数和变量节点参数特征对节点进行截断与划分，使得只有满足条件的节点参与迭代运算。此外，基于外信息频率对预测符号进行截断，只选取最可能的有限域符号进行翻转和预测。仿真和数值结果显示，TD-SFDP算法能够在性能损失可控前提下，减少每次迭代的运算操作数，从而降低算法译码复杂度。

2 系统模型和符号定义

3 低复杂度符号翻转多元LDPC译码

3.1 基于加性参数的改进型wtd-AlgB算法

文献[13]提出了一种基于符号翻转的加权多元LDPC译码算法(wtd-AlgB)：把汉明距离和多数逻辑准则进行结合，统一形成硬判决符号的可靠度量。但该算法性能受门限值和加权系数的影响较大，并且每次判决都需大量的实数域乘法操作。为降低算法复杂度和硬件实现能耗，在此对原算法进行修正和改进，描述如下：

基于上述信息处理的算法简称为Iwtd-AlgB，描述如表1所示。

本文后续的仿真实验显示，当把距离参数调整到合适范围，改进的Iwtd-AlgB算法在译码性能上与原算法相当，但改进算法避免了浮点乘法运算，降低了每次迭代的计算能耗。

表1 Iwtd-AlgB算法

3.2 基于截断型的预测机制符号翻转译码算法(TDSFDP)

文献[17]提出一种结合了汉明距离参数和预测机制的多元LDPC符号翻转译码算法(D-SFDP)。与传统的广义Gallager算法B(AlgB)及其基于距离的改进版(wtd-AlgB)不一样，D-SFDP译码算法有两个显著特征。首先，D-SFDP算法不仅考虑了符号翻转之前的距离度量，还把符号翻转后引起的目标函数的变化考虑进来，使得译码器能够根据这种变化估计和预测最可能翻转的符号。其次，D-SFDP算法不使用简单的伴随式而是基于外信息来计算距离参数。这样，每个校验节点到变量节点的可靠度量信息即可区分开来。同时，由于汉明距离源于有限域符号的二进制表示，D-SFDP算法实际上也结合了有限域的结构特征。仿真显示，D-SFDP算法能够获得比传统符号翻转算法更加优秀的译码性能。

表2 TD-SFDP算法

4 复杂度分析

表3 译码算法每次迭代的计算复杂度比较

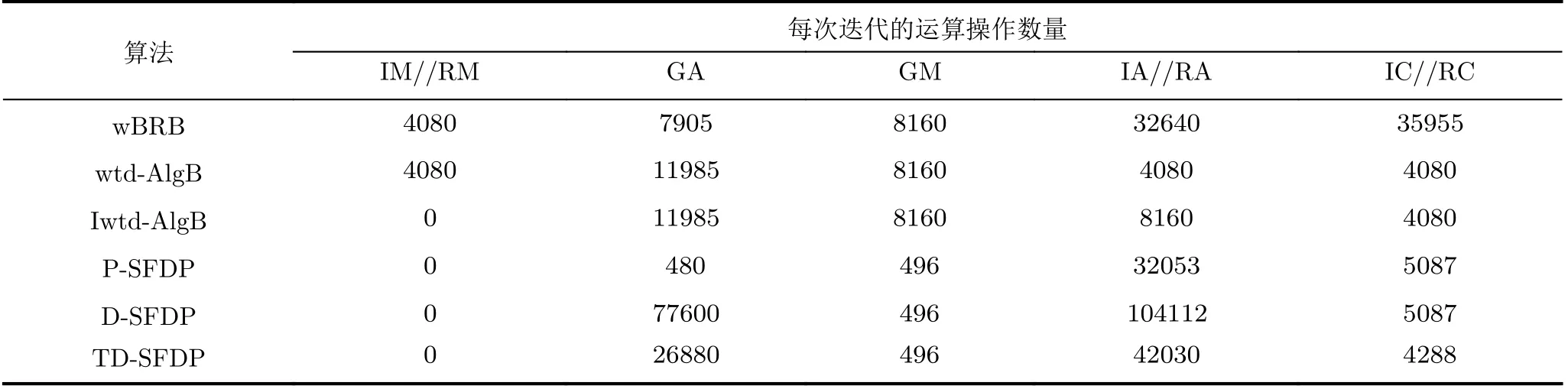
表4 F 16(255,175)多元LDPC码的每次迭代译码算法复杂度

5 译码性能仿真实验

译码性能如图1所示，由图可见：(1)本文提出的Iwtd-AlgB算法与wtd-AlgB算法性能相当，但由于避免了译码过程中的乘法操作，因此降低了每次迭代的计算复杂度；(2)D-SFDP算法和P-SFDP算法性能相当(差距在0.1 dB以内)，且由于没有进行截断处理，其性能表现最佳；(3)经不同程度截断处理的TD-SFDP算法存在不同程度的性能损失。具体地，当 T1=T2=0 时对应原算法；随着T1, T2的增大，算法的复杂度将得到优化(下降)，但也会带来性能上的下降。例如：在BER=10-4时，门限值T1=4, T2=2 和T1=4, T2=3的TD-SFDP算法，其性能分别比D-SFDP算法下降了0.18 dB和0.25 dB。

图1 F 16(225,147)多元准循环LDPC码译码性能

算法平均迭代次数如图2所示，由图2可见：(1)在中低信噪比区域，D-SFDP算法，P-SFDP算法和小门限值的TD-SFDP算法平均迭代次数相当，但低于门限值较大的TD-SFDP算法。例如，在SNR=4.0 dB时， T1=4, T2=3的TD-SFDP算法的平均迭代次数约为46 次；明显大于原算法的37次；(2)在高信噪比区域，D-SFDP, P-SFDP算法和TD-SFDP算法的迭代次数基本一致；(3)在高信噪比区域，wtd-AlgB算法与本文的Iwtd-AlgB算法的平均迭代次数更小，这是因为D-SFDP, P-SFDP算法和TD-SFDP算法每次迭代只允许翻转1个符号。

实验2 考虑基于有限几何构造的F16(255,175)规 则准循环LDPC码[23]，该码行重ρ =16，列重 γ =16 ，码率R =0.68。参数设置如下：(1)对于wtd-AlgB算法，距离参数 θ =(2.1,2.0,1.0,1.0)，对于Iwtd-AlgB算法， θ =(4.0,3.5,1.0,1.0)；(2)对于D-SFDP算法和TD-SFDP算法，距离参数统一选取为θ =(3.0,1.4,1.2,1.0)； (3)对于P-SFDP算法，η =(0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0,1.2, 1.3, 1.4, 1.5, 2.0, 2.0)为其外信息加权系数。各算法的门限参数在图上标出。

译码性能和迭代次数如图3和图4所示，由图可观察到类似的结果，即本文提出的两种降低复杂度的多元LDPC符号翻转译码算法与原算法相比，在适当的参数设置下，译码性能保持不变或者以牺牲一定性能为代价，换取复杂度方面的降低。具体地：(1)结合了外信息和距离参数的Iwtd-AlgB符号翻转算法与wtd-AlgB算法的性能相当；(2) D-SFDP 算法和P-SFDP算法性能最佳，均优于Iwtd-AlgB算法，在 BER=10−4时获得了约0.9 dB的性能增益；(3)经不同程度截断处理的TD-SFDP算法存在不同程度的性能损失，门限值T1, T2越大，性能下降越多。在算法的平均迭代次数方面，也得到与实验1类似的结果。

图2 F 16(225,147)多元准循环LDPC码平均迭代次数

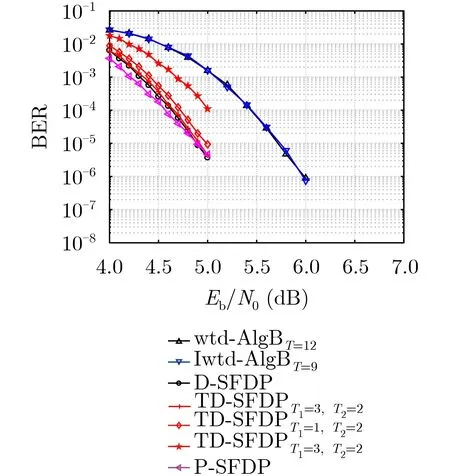
图3 F 16(255,175)多元准循环LDPC码译码性能

图4 F 16(255,175)多元准循环LDPC码平均迭代次数

6 结论

本文提出了两种基于符号翻转的低复杂度多元LDPC译码算法，Iwtd-AlgB算法将翻转度量函数修正为外信息频率和距离参数的简单求和，降低了复杂度；TD-SFDP算法根据参数和外信息特征对节点和有限域符号进行截断与划分，使得只有部分比例的节点和符号参与迭代过程中的处理和翻转预测，从而降低每次迭代的译码复杂度。仿真结果表明：两种改进算法的译码性能与原算法相差不大，适当调整参数，可在性能和复杂度之间进行折中。复杂度数据显示，第1种算法避免了原算法的实数乘法操作；第2种算法的有限域加法运算次数约为原算法的 35%，整数/实数加法运算次数约为原算法的 40%。此外，本文提出的截断阈值基于外信息频率设计，仍属于多数逻辑范畴，因此对于列重较大LDPC码的复杂度降低效果尤为明显；当列重减少时，截断集合的阶与原算法参与运算的节点/符号数目基本一致，其复杂度降低效果有限。