非平稳信道下的鲁棒数据链优化设计综述——带限环境下的混沌传输系统

苗美媛 宋 丹 徐位凯 湛 佳 王 琳*

①(厦门大学信息学院 厦门 361005)

②(香港理工大学电子与信息工程学院 香港 999077)

1 引言

以万物互联为中心的第6代移动通信(6G)将低成本低功耗作为主要目标，因此一些具有相关特性的技术将受到广泛关注。其中传统的信号处理技术的新设计引起了研究单位、高校和业界的广泛关注，然而还有一些重要的问题有待我们解决。如何利用低成本低功耗技术在带限非平稳环境下实现鲁棒的数据传输将是一个重要的研究方向。混沌通信以其低互相关、良好的自相关和宽带频谱特性，在扩频通信系统中得到了广泛的关注，且实现简单，无需混沌信号同步，因此可以成为低成本低功耗方案的有利候选者。以往对混沌通信方案的研究，如混沌移位键控(Chaos Shift Keying, CSK)[1]，即混沌信号需要在接收端同步。为了有效避免混沌序列的恢复失真，针对非线性系统，提出了一种无需复制混沌序列精确副本的非相干调制方法，称为差分混沌移位键控(Differential Chaos Shift Keying,DCSK)[2]，针对恒定功率系统，提出了调频DCSK(Frequency-Modulated Differential Chaos Shift Keying, FM-DCSK)[3,4]。在DCSK中，利用两个带有混沌信号的时隙来传输1个比特，分别称为参考混沌信号和信息承载混沌信号。通过与参考信号和信息承载信号的相关来判断发送的比特，因此无需特定混沌信号的恢复和接收机的信道估计器。同时，两种信号能够有效地抵抗严重的多径衰落和符号间干扰。

然而，传统的DCSK存在能耗高、频谱利用率低、数据速率低等缺点。为了改进DCSK系统，人们做了许多工作，如改进的DCSK(Improved-Differential Chaos Shift Keying, I-DCSK)[5]和相位分离DCSK(Phase-Separated Differential Chaos Shift Keying, PS-DCSK)[6]，均是用正交正弦载波而非时延来区分参考信号与信息承载信号。另外，提出的降噪型DCSK(Noise Reduction Differential Chaos Shift Keying, NR-DCSK)[7]能够适应有噪信道同时降低系统能耗。

为了提高频谱利用率，一些工作研究了多载波调制，如在高斯白噪声(Added White Gaussian Noise, AWGN)信道上提出了多载波DCSK系统(Multi-Carrier Differential Chaos Shift Keying,MC-DCSK)[8]和其MDCSK版本(Multi-Carrier M-ary Differential Chaos Shift Keying, MC-MDCSK)[9]。文献[10]提出了两种广义载波指数MDCSK(Carrier Index M-ary Differential Chaos Shift Keying,CI-MDCSK)方案，并对两种方案进行了讨论。文献[11]提出了一种能抑制信道噪声的多载波差分混沌移位键控(Subcarriers Allocation M-ary Differential Chaos Shift Keying, SA-MCDCSK)系统。为了克服低数据率的缺点，在文献[12-20]中提出了一些改进的DCSK方案，利用沃什(Walsh)码实现了两比特和多比特的正交信号，并用索引调制(Index Modulation, IM)[21]及混合方式实现了DCSK系统[17]。如码索引调制的DCSK(Code Index Modulation Differential Chaos Shift Keying, CIM-DCSK)[18]、码索引调制的多级码移位DCSK(Code Index Modulation Multilevel Code Shifted Differential Chaos Shift Keying, CIM-MCS-DCSK)[19]和具有较高频谱效率的通用码移位DCSK(Code Index Modulation Code Shifted Differential Chaos Shift Keying, CIM-CS-DCSK)[20]。这些方案利用索引携带一部分比特，DCSK携带另一部分比特，实现了一个时间周期内的m bit传输。此外，交换码索引DCSK(Commutation Code Index Differential Chaos Shift Keying, CCI-DCSK)[22]使用参考混沌信号的交换副本来映射额外的比特以在同一个时间段内实现多个比特，并且在正交多级DCSK(Orthogonal Multi-level Differential Chaos Shift Keying, OMDCSK)[23]方案中从参考信号的一组正交信号形式中选择信息承载。

DCSK与索引调制相结合虽然能提高数据传输速率，但硬件复杂度呈指数级增长。因此，寻求复杂度低的方式提高数据率成为主要研究方向之一。文献[24]提出了一种在第1周期发送参考信号的正交混沌移位键控(Quadrature Chaos Shift Keying,QCSK)结合参考信号希尔伯特变换和延迟参考信号形式的映射2位符号。文献[25]提出了一种高复杂度的MIMO型的MDCSK。文献[26]基于文献[24]与多进制相移键控(M-ary Phase Shift Keying,MPSK)星座图相结合提出一种MDCSK，该星座图通过MPSK星座图传输多进制符号的两个正交信号作为信息承载部分，并分别对基于MPSK的MDCSK的系统进行了比较。其中，与具有较好的误码率性能PSK星座以及DCSK相比，MDCSK具有更好的误码率性能。此外，在信息承载部分文献[27]提出了基于M元PSK和QAM的方案，利用MPSK和MQAM调制M元符号的参考混沌信号。采用非均匀间隔相位星座的多分辨MDCSK(MultiResolution M-ary Differential Chaos Shift Keying, MRMDCSK)调制[28]是一种具有应用前景的技术，它能够在一个符号内满足不同的误码率要求，从而提高比特的数据速率。文献[29]提出了一种新的基于非均匀距离星座映射的分层平方星座MDCSK，针对信道特性[30],它在最后一个分层上修正两个星座点之间的距离，克服了调制阶数越大时误码率性能下降的问题。

对于一些实际环境，如在带限环境下，需要在不扩展带宽的情况下提高系统的误码率性能，就需要编码调制的引入，能够在不扩展额外带宽的情况下获得较高的编码增益。如在多径信道中结合文献[26]中的MDCSK(后面无特殊说明均为此MDCSK)与网格码提出一种新型的网格编码差分混沌调制(Trellis-Coded Differential Chaotic Modulation,TC-DCM)[31]。并在此基础上，文献[32-34]针对不同情况对其系统的编码方案以及系统方案进行改进。此外，通过将低密度奇偶校验(Low-Density Parity-Check, LDPC)码与MDCSK结合提出了一种基于星座的差分混沌比特交织编码调制(Differential Chaotic Bit-Interleaved Coded Modulation, DC-BICM)系统[35]，能够在有效降低误码率的同时保证多径信道环境的鲁棒性。这些方案均为非平稳环境下的系统设计提供有力依据。

本文主要介绍了面向6G中非标准信道环境下基于低成本低功耗的几种MDCSK(圆形方形)的信号设计以及相应的编码调制系统分别针对具体非平稳信道环境下所实现的系统优化，并给出了未来发展方向。首先，针对用于该系统的MDCSK系统模型进行了介绍。其次，对系统本身优化以及基于MDCSK的编码调制相关的研究工作进行了介绍。继而通过举例论证基于MDCSK系统的星座以及相关调制编码的结构、码型及相关算法设计与优化，能够在不扩展带宽的情况下显著改善系统性能，实现了低功耗。以此为针对非平稳信道下的MDCSK数据链路优化设计提供些许思路，并且举例说明在具体非平稳环境下的应用方案，为其他现有环境中低成本低功耗的实现提供可能。最后，给出了未来的研究工作讨论，如针对非平稳信道特性系统参数的优化与自适应传输机制等问题。供感兴趣的读者参考和推进。

2 DCSK相关基础：模型与基础特性

DCSK调制方式最早由Kolumban等人[2]提出，作为一种具有鲁棒性的调制方式。首先产生扩频的混沌信号作为原始的参考信号，通过延时T时间产生信息承载信号，由参考信号的“正”“负”来表示“1”“0”。接收端通过直接相关t1, t2时间段的信号而获得传输信息，无需信道估计。其具体正，负信号可以分别表示为

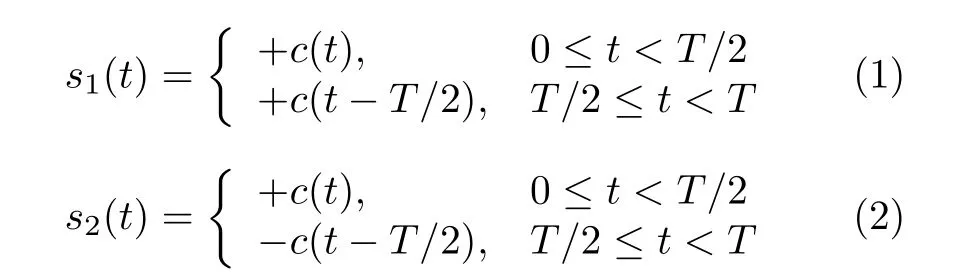
此调制方式无需载波同步仅需信号同步、非相关检测，实现设备简单以及在多径衰落信道下具有鲁棒性等特点，相应的传输速率随之下降。为了解决速率低的问题，QCSK[24]以及一系列的MDCSK被相继提出[23,25,26]。其中主要包括两种方式，一种是通过星座的方式实现多比特传输[26-29]，另外一种是通过与其他技术相结合如指标调制等方式实现多比特数据传输[12-20]。本文将主要针对第1种方式展开介绍。

2.1 圆形星座下的MDCSK及星座优化

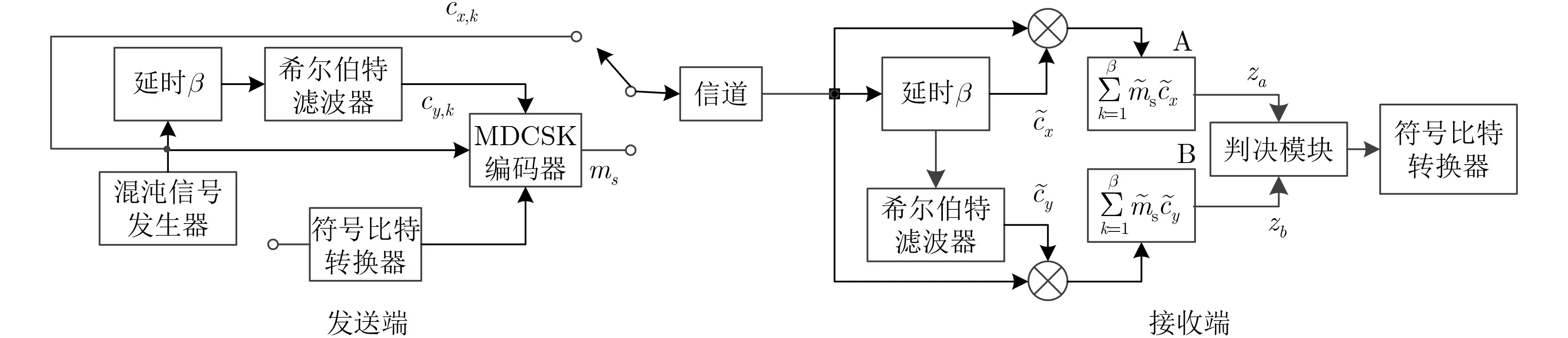
图1 MDCSK的系统框图

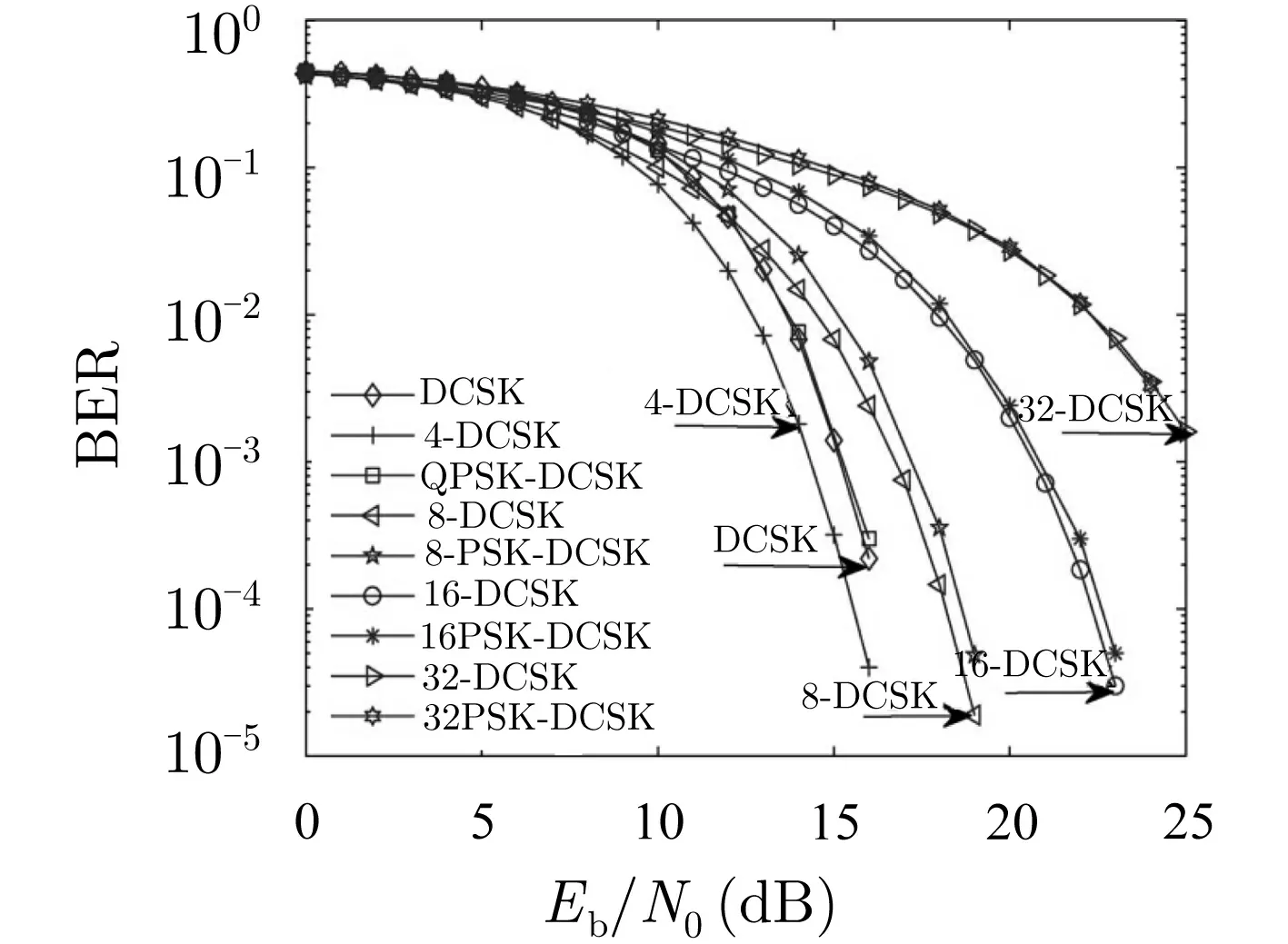
图2 MDCSK和MPSK-DCSK在扩频因子β=60，M=2, 4, 8, 16, 32的误码率性能曲线

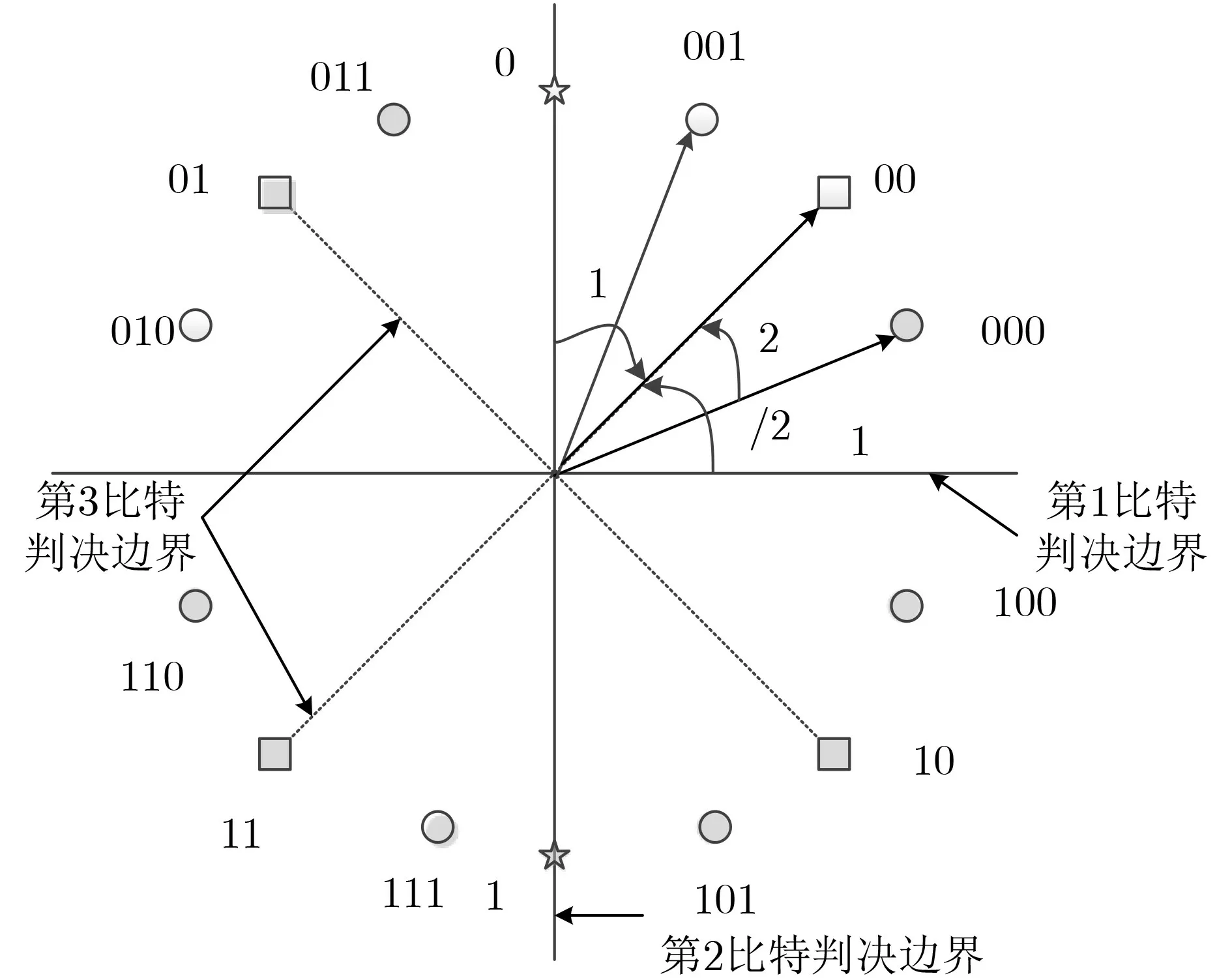
图3 一般化MR-8元DCSK星座及其灰编码映射与判决边界

图4中，研究了AWGN信道下不同相位向量对2/4/8/16-DCSK系统性能的影响，其中，相位向量设置为 θ =[π/5 π/25 π/40]。扩频因子β=128。可以观察到，提高第1个保护相位BER性能得到改善，这种现象类似于信道编码，但是该系统不需要展宽带宽。从图可以看出，当相位 θ1≤ π/4时，最高优先级比特和第2优先级比特要互换，即二进制DCSK星座在x轴上。

因此，文献[26]中在实现MDCSK的同时，通过星座优化对系统进行了改进，在不增加带宽的情况下，不同数据优先级的误码率性能满足不同的业务需求。此外，它还继承了传统DCSK系统的优点，具有良好的抗多径衰落性能。

2.2 方形星座下的MDCSK以及星座优化

不同于上面所述的圆形星座，对于正方形、矩形、十字形和星形星座，需要信道估计器模块[27]。但是与传统的信道估计不同，只需要部分信道估计便可以实现解调。因此，文献[27]中设计了一种方形星座MDCSK，分析了该系统的峰均功率比(Peakto-Average Power Ratio, PAPR)性能，并给出了详细的理论公式推导。此外文中还基于方形星座M-DCSK设计了一种结构简单的最小二乘(Least Square, LS)估计器以便于解调。

在此文献中，与传统的相干信道估计不同的是，只需要得到文献[30]中定义的信道功率值，而不需要得到每个信道系数。我们假设估计的信道状态信息是。之后，归一化判决向量变为z′=z/(Ep为平方根升余弦滤波器p(t)的能量)，该值将用于根据图5所示的判决边界对接收到的符号进行解码。

从图5中可以看出，与图6(a) (使用的参数为M=4, 16, 32, 64和β=320)中的p-CSI(完美-信道状态信息)方案相比，所提出的LS估计器方案具有约1 dB的性能损失。与图6(b)中的圆形系统相比，S-16/64-DCSK系统显著改善了误差性能。因此通过分析和仿真结果表明，与C-M-DCSK系统相比，该系统在多径衰落条件下能实现较低的功耗，但具有较高的峰均比。

图4 AWGN信道下，2/4/8/16-DCSK系统的BER性能

综上所述，通过星座的方式可以实现信号速率的提升，同时能够实现不同环境下的系统性能提升。虽然基于平方星座的DCSK系统需要信道估计器，但其误码率性能远优于基于圆形星座的DCSK系统(见图6(b))，在能量消耗方面，基于方形星座的DCSK系统比基于圆形星座的DCSK系统效率更高。其他类型的星座(如矩形、十字形和星形)也可用于一般化系统框架，因此具有更广阔的应用前景。此外，针对文献[26]中的多分辨率M-DCSK框架，可以设计一个基于多分辨方形星座的M-DCSK系统，该系统通过调整距离d来提供更灵活的误码率要求，这种情况下幅度和相位都会携带信息。

3 MDCSK的基础研究：带限系统方案设计

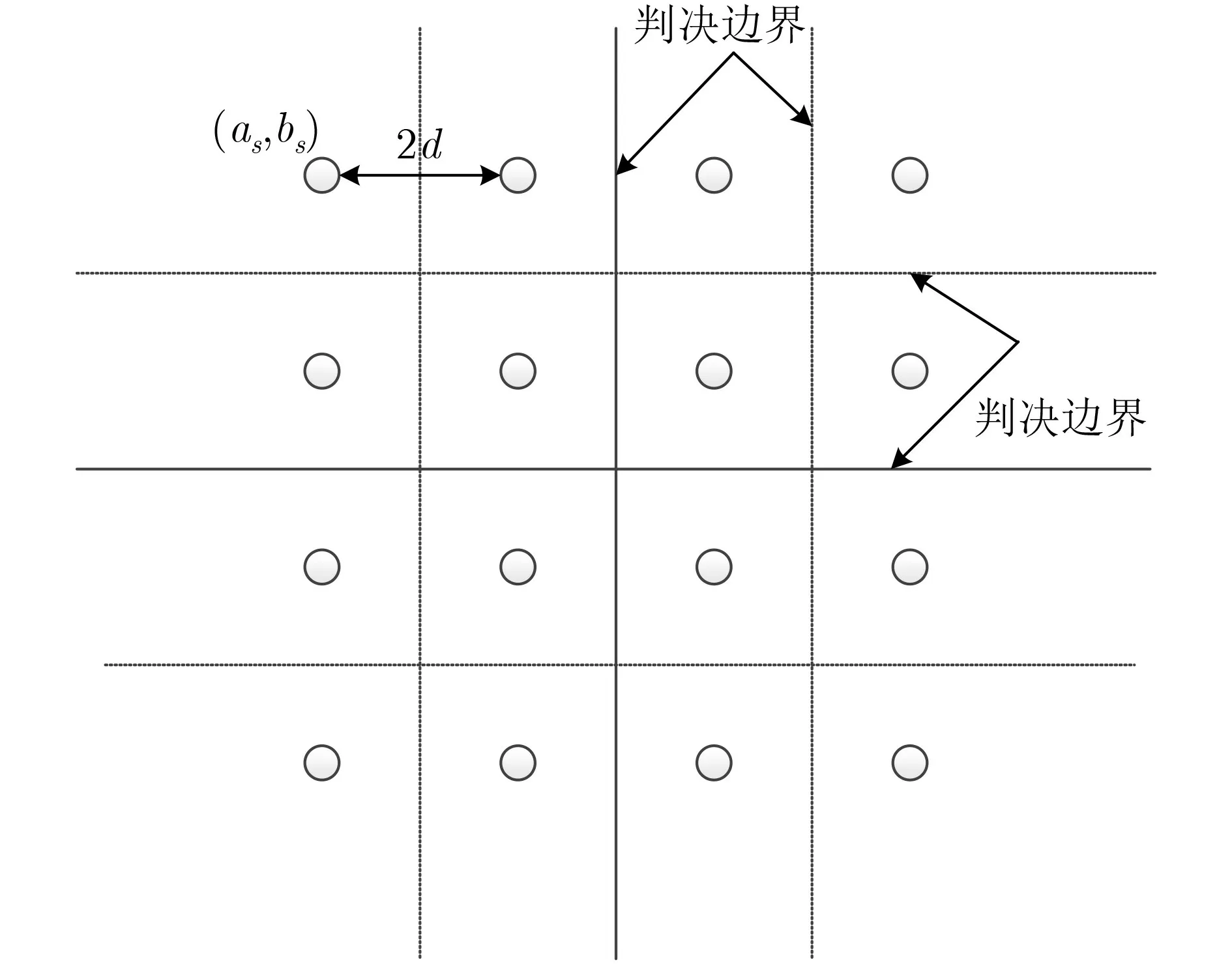
图5 方形星座图与判决边界

在MDCSK调制中，针对其信号结构以及星座进行优化能够在一定程度上有效的提高系统的误码率性能。但是，想进一步降低系统功耗，就需要引入编码方案。由于一般的编码方案与调制方式是分开设计的，因此想要引入编码方案需要额外的带宽来实现。然而在带限环境下，由于带宽较窄，直接分离式的编码方法所需要的额外带宽就无法提供，因此引入编码调制方案以便于解决带宽不足的问题。

3.1 网格编码调制(Trellis Coded MDCSK)及优化方案

3.1.1 网格编码调制方案介绍

文献[31]中提出了一种将网格编码与MDCSK相结合的新型编码调制方案-网格编码差分混沌调制(Trellis-Coded Differential Chaotic Modulation, TC-DCM)。该文献计算了加性高斯白噪声信道上MDCSK的信道容量，验证了网格编码和混沌调制相结合的可行性。同时，详细地给出了AWGN信道和瑞利(Rayleigh)平坦衰落信道下TC-DCM系统的理论误码率界的推导过程，并在8-DCSK星座，4态(4-state)2/3码率的参数下对方案进行了仿真验证。

图7(a)、图7(b)中表明该方案的理论误码率界与仿真结果基本一致。与相同带宽的未编码系统相比，不同状态、不同速率的TC-DCM系统在AWGN信道上可以获得明显的编码增益。图7(c)通过与相同带宽效率的TC-DCM系统在无CSI多径Rayleigh衰落信道下的性能相比较，结果表明此方案在非标准信道下具有良好的鲁棒性，证实了TC-DCM方案的优越性。

3.1.2 网格编码调制优化方案介绍

大部分基于网格码的编码系统直接使用简单易操作的卷积码来实现编码调制，那么是否存在更优的编码方案呢？为了获得更好性能，需要对系统进行优化设计。

文献[32]针对TC-DCM方案提出了Turbo网格编码差分混沌调制(Turbo Trellis-Coded DCM,TTC-DCM)方案。同时，文献[33]中提出其IQ方案，并且在其基础上提出了一种码搜索算法，目的是找到一个在尽可能低的信噪比(Signal Noise Rate,SNR)条件下，在相应EXIT图中存在开放通道。其具体算法流程如表1所示。

图6 多径Rayleigh衰落信道下不同系统的误码率

从文献可知，TTC-DCM方案在多径衰落信道环境中，BER=10-5的情况下比TC-DCM方案获得4 d B 的增益。同时利用I Q 交织器在平坦的Rayleigh衰落信道和多径Rayleigh衰落信道中提供空间分集。与TTC-DCM相比，IQ-TTC-DCM方案在衰落环境下能获得更好的性能。

为了进一步提升文献[31]中在传输环境较差时的BER性能。文献[34]提出了一种串行级联网格编码差分混沌调制(Serial Concatenated Trellis-Coded Differential Chaotic Modulation, SCTCDCM)系统。经文献[34]研究分析发现，SCTCDCM系统比TTC-DCM系统在相对高SNR下能获得更好的BER性能，同时在BER=10-8之前都不会产生错误地板。

由此可以看出，TC-DCM具有高带宽效率、抗多径、低成本和低复杂度的特点，是一种适用于严重多径传播的带限通信系统的方案。

3.2 原模图低密度奇偶校验码的编码调制(P-LDPC coded MDCSK)方案

上述已经阐述了网格编码对于系统性能的影响，事实证明基于网格编码的编码调制方案可以有效提高在非标准环境下的BER性能。那么其他编码对于系统性能影响又如何呢？

文献[35]根据文献[36,37]提出了一种利用P-LDPC码[38,39]构建基于星座的差分混沌比特交织的编码调制系统(Differential Chaotic Bit-Interleaved Coded Modulation, DC-BICM)。

通过文献[35]的分析可知，DC-BICM系统存在最佳的扩频系数和最佳的迭代译码值，随着码长的增加，系统性能变好，但随着码长的持续增加，系统性能变差。图8通过与非编码的方形的4-DCSK的误码率性能比较可知，在BER=10-4, 2β=64的情况下DC-BICM可以获得12.5 dB的增益。图9对DC-BICM和BICM DS/SS系统的比较，表明该系统具有较低的复杂度和在部分信道响应下有较好性能。此外，通过与具有相同频谱效率的方形星座MDCSK系统的比较，验证了该系统在不增加带宽的情况下具有较高的编码增益，在抗多径衰落方面具有良好的性能。

综上所述，对于带宽受限的情况下，选择合适的码型与MDCSK构建编码调制方案可以在信道环境恶劣且不扩展带宽的情况下有效的提高系统性能。同时针对具体IoT环境下应用环境，需要针对具体情况再设计以便于取得性能和资源在IoT应用下的平衡。

图7 不同信道下误码率比较

表1 EXIT码型搜索算法流程

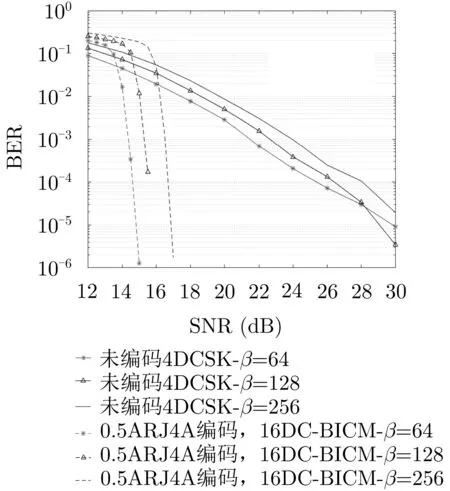
图8 码率1/2的ARJA-16-DC-BICM与方形的4-DCSK的误码率性能比较

4 应用研究：非平稳信道下的编码调制与多载波方案

4.1 MDCSK在电力线通信(PLC)中的分析与优化

4.1.1 PLC环境下MDCSK的性能分析

前面讨论了MDCSK及其编码调制方式在多径衰落信道的性能特性，由此可知，MDCSK在衰落信道下具有良好的鲁棒性。那么，在现有的PLC环境下是否也具有鲁棒性呢？

文献[40,41]中讨论了DCSK及MDCSK在PLC的回波模型[41]下的性能。根据文献中所述，作者选择了服从泊松分布的混合高斯噪声模型[30,42]作为PLC信道下的噪声，其由脉冲噪声与相位噪声组成，在此信道环境中搭建MDCSK系统并与传统的调制方式进行比较。

因此，文献[41]将MDCSK系统与DS-MDPSK系统在不同信道参数的情况下进行了比较，如表2所示，其中结果如图10，显示了在此信道环境下MDCSK方案均显著优于DS-MDPSK方案，说明了MDCSK系统在PLC信道下通信的优越性。

4.1.2 PLC环境下基于MDCSK的编码调制方案

4.1.1中充分表明了MDCSK在PLC环境下的优越性能，但是当系统误码率达到一定程度的时候均会出现错误地板。为了进一步解决这个问题，文献[43]利用文献[42,44]中的方法，提出了一种基于星座的PLC信道下迭代接收差分混沌比特交织编码调制系统(Differential Chaotic Bit-Interleaved Coded Modulation with Iterative Receiver, DC-BICM-IR)，并设计了一种新型的P-LDPC码, 选取文献[45,46]中的信道模型作为参考。为了减轻脉冲噪声的影响，文献[43]先在DC-BICM系统框架中引入混合滤波器(Myriad Filter, MyF)，而后为了进一步消除余留的脉冲噪声及码间干扰(InterSymbol Interference,ISI)带来的影响，引入迭代接收(Iterative Receiver,IR)结构，构成DC-BICM-IR系统。图11为引入IR结构与新码型设计的性能分析。

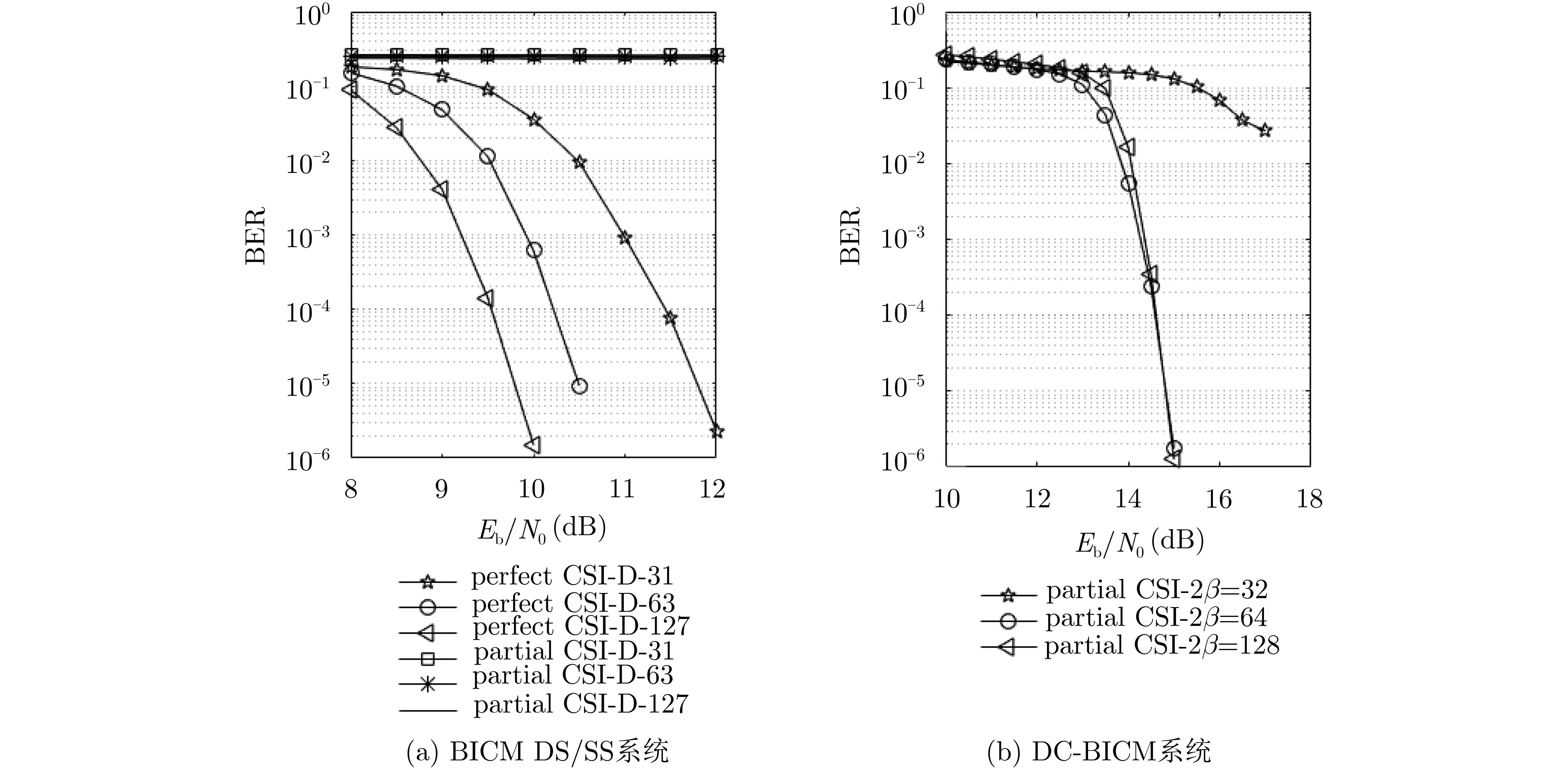
图9 BICM DS/SS-5 DC-BICM系统误码率比较

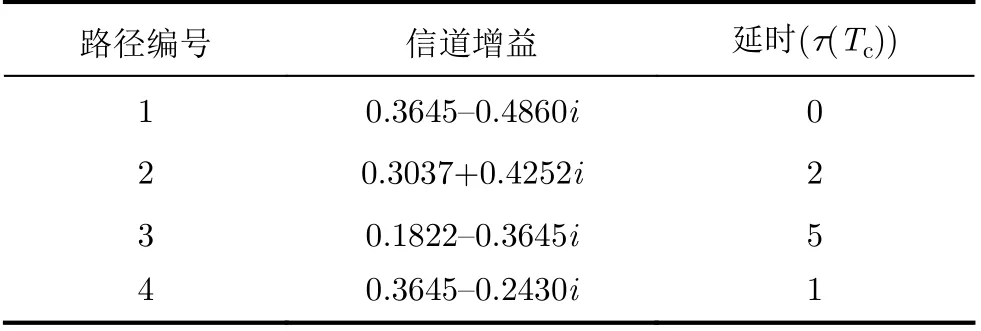
表2 多径PLC信道参数

图10 多径PLC信道下BER性能比较

图11(a)显示了在PLC信道下，DC-BICM系统使用和未使用MyF的BER性能对比曲线。从图11(a)中可以看出，在α=1, 1.5时，由于脉冲噪声的干扰，当前的校验与系统信息被严重污染，给译码器带来了严重的错误影响，导致系统瘫痪。由于MyF的引入，极大地削弱了脉冲噪声的影响，使得系统在一些恶劣的环境下(如α=1, 1.5)仍能正常工作。同时，引入IR能够在BER=10-6的情况下带来0.4～0.5 dB的编码增益。另外 从图11(b)中可以看出，在BER=10-6的情况下，I-ARJA码的性能优于AR4JA码约0.6 dB。由此可以看出，MDCSK不仅相对于传统调制方式在PLC信道环境下更加鲁棒，选择合适的优化方法还可以有效地消除错误地板并且获得更好的BER性能。

4.2 DCSK在水下信道(UWA)中的分析与优化

针对4.1节中讨论了MDCSK在PLC中，相比其他调制方式在非平稳信道下有较好的鲁棒性，因此一些学者将其延伸到水下环境进行讨论。文献[47]根据文献[48]的信号环境将码移差分混沌键控(Code Shifted Differential Chaos Shift Keying, CS-DCSK)与正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)相结合并讨论了其在水下信道(UnderWater Acoustic, UWA)的性能。此外，在码片上使用循环移位交织器来获得频率分集。为了深入了解该系统，推导了该系统在高斯信道和多径Rayleigh衰落信道下的误码率，并通过仿真进行了验证。此外，还分析了该系统的频谱效率，并与现有的混沌通信系统进行了比较。

为了使仿真更具说服力，根据文献[47]所得到的1500个时变信道脉冲响应卷积的仿真结果，其中有3个通道场景如图12。

进一步，根据图12中信道模型进行仿真比较，如图13所示, 参数为：扩频因子32，子载波N=[16,32, 64, 128, 256]，循环前缀的长度 cp=Ts/δ。结果表明，在两个信道下，该系统的性能优于MC-DSSS,MM-DCSK和OFDM-CS-DCSK。

由此可见，文献[47]所提方案是基于无信道估计和均衡的非相干接收机，因此更加适合于具有时变特性而难以跟踪和估计的UWA通信场景。

综上所述，通过在PLC与UWA环境下对DCSK的性能分析与研究可知，由于此调制方式无需信道估计与均衡等优势，在非平稳信道下的鲁棒性优良，对于目前难以跟踪与估计的信道来说无疑是一种很好的选择。

5 结束语

随着物联网时代的日益发展，前期人们已经享受到由于通信速率的提升所带来的便利，将更多的关注到如水声、电力线通信等非平稳信道中鲁棒、低功耗的传输技术方案。DCSK作为低成本、低功耗的调制技术，实现简单且在非标准环境下有良好的鲁棒性，成为了下一代非平稳传输环境的有利候选者。如何在现有研究基础上对于更多具体的非平稳应用环境进行分析及优化仍然是一个值得继续探究的问题。文本主要针对DCSK的带宽效率优化、带限环境下基于MDCSK的编码调制技术的实现与优化、具体实际环境下DCSK的相关性能分析与系统改进等方面入手进行了综述。从整体来看，通过星座实现多元的方式可以在有效的提高系统数据传输速率的同时保证系统的复杂度无需呈指数型增长。同时对于带宽受限的情况下，编码调制技术可以在不扩展带宽的情况下实现MDCSK误码率性能的进一步提高。最后一个案例探讨了几种具体环境下DCSK的性能优越性以及给出对应优化方案的设计思路。这些工作与设计思想也将为其他类型的调制优化方案提供一些灵感，以便于更适用于现代通信中多样的需求。

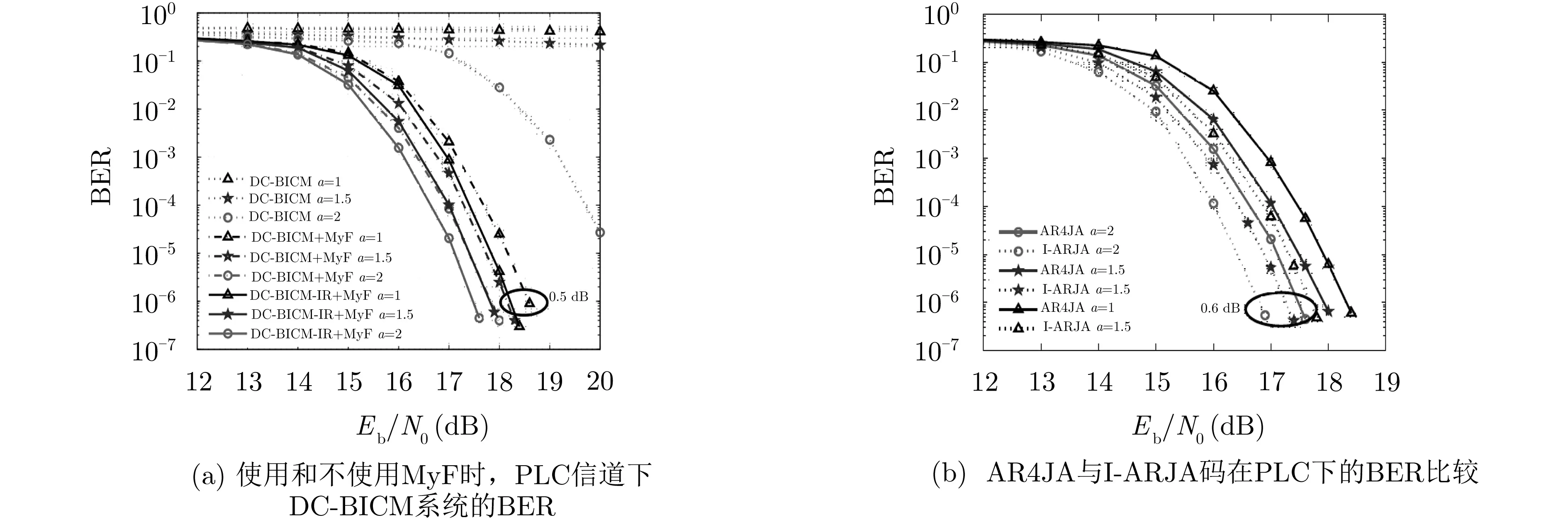
图11 PLC中误码率比较

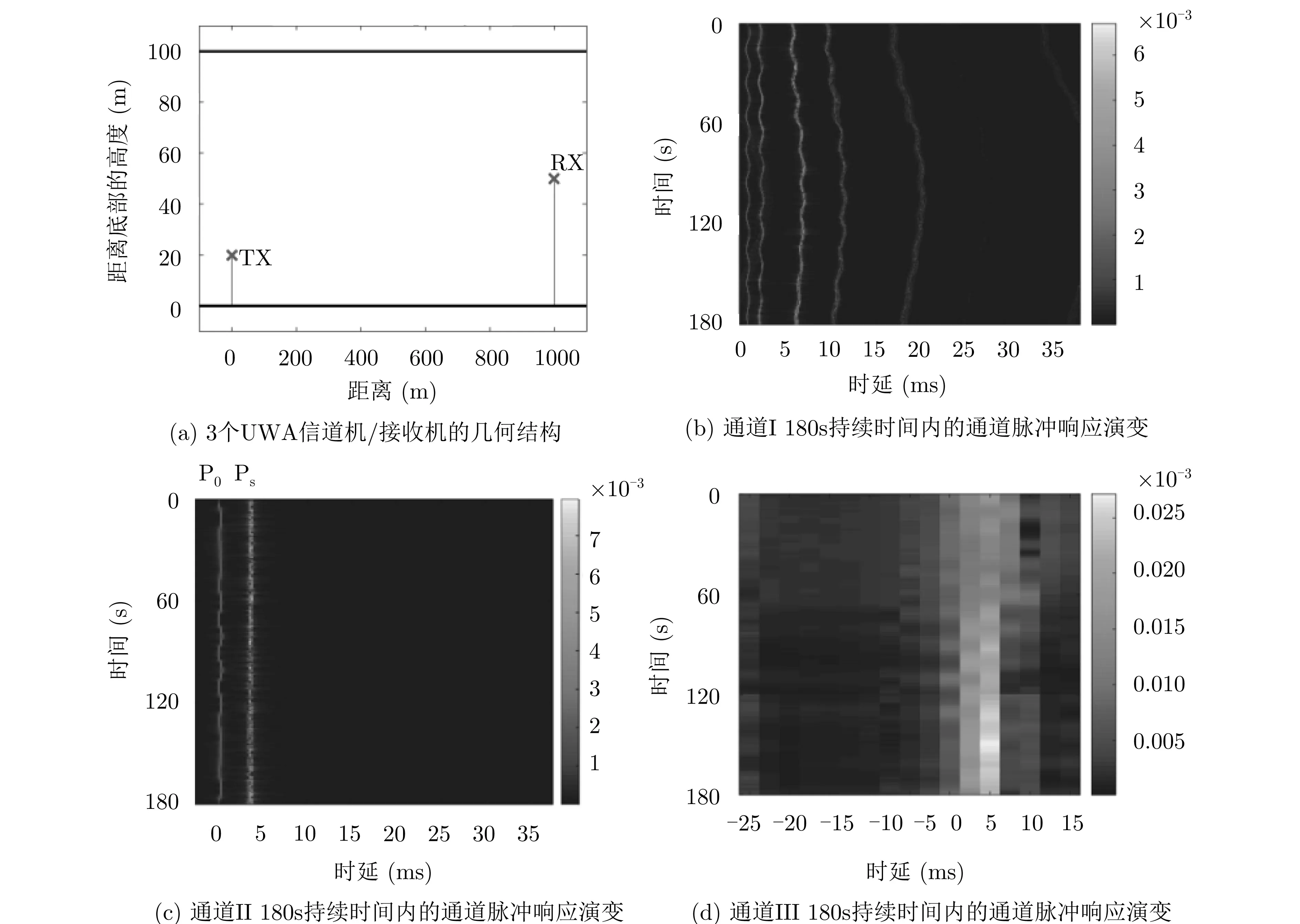
图12 时变UWA信道3个通道场景及脉冲响应

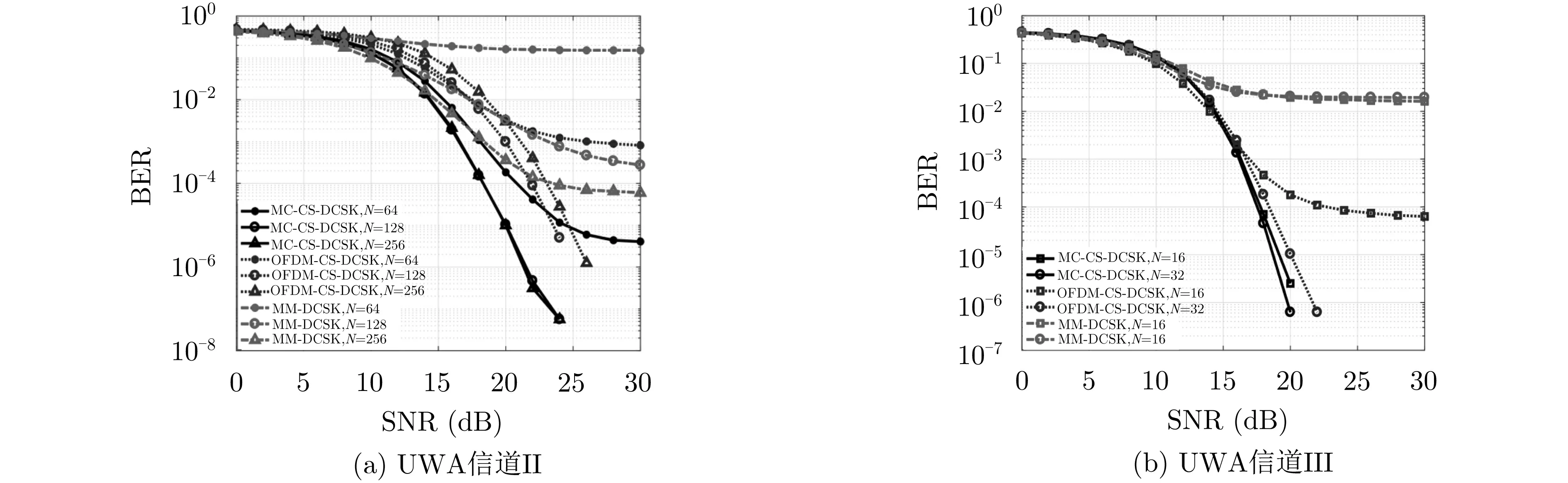
图13 不同UWA信道下MC-CS-DCSK,OFDM-CS-DCSK和MM-DCSK的误码率性能比较

该研究领域已经引起不少学者的关注，未来尚有诸多问题需要解决,其中主要有以下两点：

(1) 为了提高非标准信道下低复杂度、低成本的误码率性能，可以考虑在具体信道下对MDCSK进行优化。

(2) 为了进一步提高带限信道下的性能，可以考虑具体信道上编码调制的优化，包括星座与码型等优化。同时如何平衡窄带系统下设备资源与功耗之间的平衡也是需要关注的问题。

因此，此研究方向在未来还有很多的热点问题有待研究与发展。