不同级配矸石压实特性数值模拟研究

程立朝，秦义岭，李新旺，赵新元

(1.河北工程大学矿业与测绘工程学院，河北 邯郸 056038；2.河北工程大学河北省高校煤炭资源开发与建设应用技术研发中心，河北 邯郸 056038)

综合机械化固体充填采煤技术是一种绿色开采技术[1-2]，具有方便、快捷、廉价的优点，其中矸石是一种极好的固体充填材料。矸石作为充填材料，自身的密实度是影响充填效果的主要参数[3-4]，影响矸石密实度的主要因素是矸石颗粒的粒径和配比。针对不同粒径和级配下矸石材料的压实特性，涂强等[5]研究了矸石散体不同级配与压缩量的关系，得到了压缩过程中的轴向应力-应变曲线；王文等[6]研究了粒径级配、轴向应力对矸石散体压实度的影响；胡炳南等[7]采用大容器、大粒径、大载荷和数值模拟方法进行了矸石压缩试验；姜振泉等[8]重点探讨了煤矸石粒度分布的级配与压密性之间的关系；其他专家学者[9-13]也从不同方面对矸石的压实特性进行了研究，但实验室对于矸石的压实特性研究具有工作量大、材料耗费多、实验设计复杂的缺点。

本文在前人的基础上使用EDEM离散元软件对矸石的压实特性进行了研究，寻找适合矸石充填最佳粒径级配的有效方法，并在实验室重复本实验，验证EDEM离散元软件的有效性，为现场矸石充填的应用提供参考。

1 离散元法的原理和散体级配模型

1.1 离散元法基本原理

离散元法是将一个复杂的稠密颗粒集划分为相互独立的颗粒单元，对每个颗粒单元之间的相互作用使用牛顿运动学定律进行单独研究，并通过循环迭代的方法更新和确定每一个颗粒的位置来观测整个颗粒集运动状态的方法。 颗粒的运动方程见式(1)。

(1)

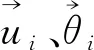
采用中心差分法对式(1)进行积分，以迭代时间步长的中点表示计算更新速度，以此计算下一时间步长的位移，见式(2)。

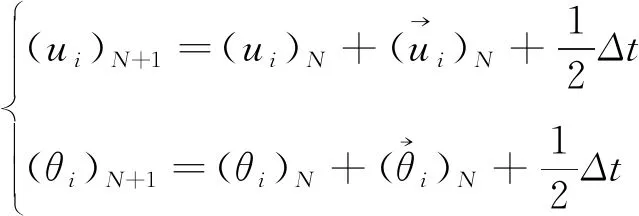
(2)

式中：N为对应的时间；Δt为时间步长。

将式(2)的计算结果带入到接触模型中可求得所需要的接触力，再经过数次迭代计算，则可以分析出颗粒在某个时间段的运动状态。

1.2 散体级配与泰波公式

富勒(Fuller)理论认为，固体颗粒可以按照粒径的大小，不同的粒径颗粒间相互搭配可以得到密度大，孔隙率低的颗粒集合体，颗粒级配曲线越接近抛物线，则其密度越大，孔隙率越小。泰波(Tabol)在富勒理论的基础上进行了修正，提出了泰波公式，见式(3)。

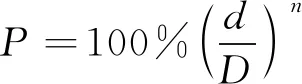
(3)

式中：P为矸石各级粒径的通过率，%；d为矸石各级粒径，mm；D为矸石的最大粒径，mm；n为泰波公式系数，是表征矸石散体中粒径分布的参数，其大小与矸石散体的孔隙率、密实度和颗粒的排列形式有关，而与矸石颗粒自身的特征无关，此次试验中取0.3～0.7。

根据泰波公式，n取值0.3～0.7时可得到连续级配矸石配比表(表1)。由表1可知，n值的增大会导致矸石颗粒级配中粒径小的颗粒占比相对降低。

表1 连续级配矸石配比表Table 1 Continuous grade gangue proportion table

2 矸石散体压缩物理模拟试验矸石散体压缩数值模拟试验

2.1 试验装置

试验采用的加载设备为长春新科YA-600型微机控制全自动压力试验机，试验系统可以自行采集试件压缩过程中的应力应变等参数，准确地反映试件的压缩破坏全过程。由于本次试验中矸石材料最大粒径为40 mm，根据能源行业标准《固体充填材料压实特性测试方法》(NB/T 51019—2014)要求：试验设计刚性筒内径不小于固体充填物料最大直径的3倍，因此本试验矸石压实模具形状设计为圆柱形钢筒，内径120 mm，壁厚10 mm，高度200 mm。试验装置实物图如图1所示。

图1 实验装置图Fig.1 The experimental platform

2.2 试验材料选取与试验结果

选取邢邯地区某矿的原生矸石作为试验的材料，对完整的块状矸石取岩芯制备直径50 mm、高100 mm的标准试件，使用三轴液压伺服试验机对标准试件进行加载，获得矸石材料的本征参数。对初步破碎的矸石使用网孔直径为10 mm、20 mm、30 mm、40 mm的筛网进行筛分，按照泰波系数的指导来配置五组质量为2 kg的矸石材料。对五组试验材料分别进行加载试验，加载方式采用位移加载方式，加载速率为0.001 m/s，数据每秒记录一次。绘制连续级配矸石压缩过程的应力应变曲线图，如图2所示。

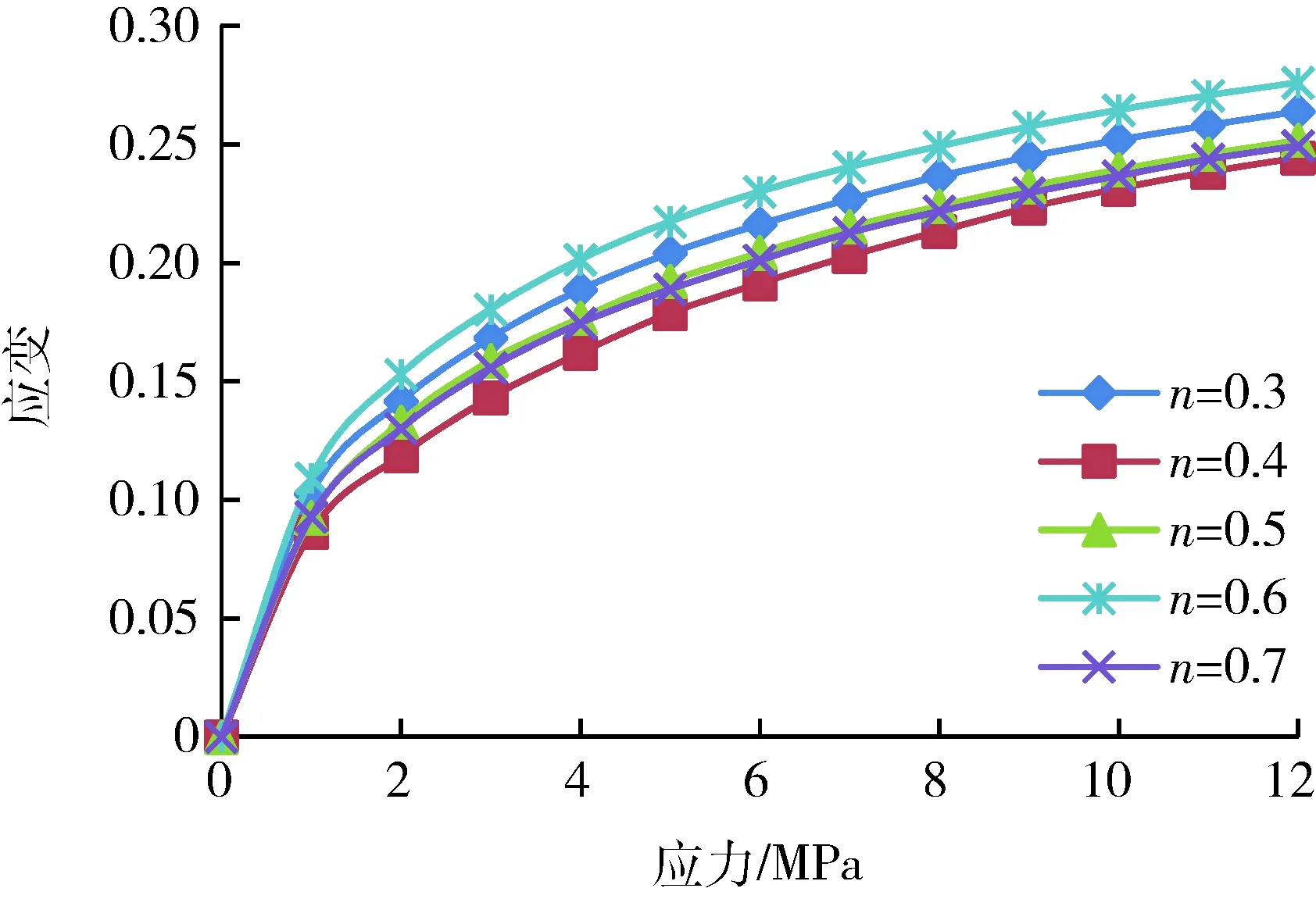
图2 物理实验连续级配矸石应力应变曲线图Fig.2 Stress-strain curves of physical experiment of continuously-graded gangue

3 矸石散体压缩数值模拟试验

3.1 颗粒创建与颗粒接触模型

利用傅里叶级数分析方法对矸石颗粒形状的几何参数(长度、宽度和高度等)进行定量分析，最终通过形状指数和形状系数对矸石形状进行分类，得出矸石颗粒主要有锥形、棱柱形、椭球形、片形和圆柱形五种形状，再对各粒径中不同形状的矸石颗粒数量进行统计，提高数值模拟试验的准确性。采用矸石颗粒的典型形状图形在ProE软件中建立三维模型，再将其三维模型文件在EDEM中加载并使用多球体组合的方式创建典型矸石颗粒形状模型。典型矸石实物形状与对应颗粒形状模型如图3所示。

图3 典型颗粒形状模型Fig.3 Typical shape model of gangue

由于矸石颗粒间黏聚力基本为0，因此本次数值模拟试验颗粒接触模型采用Hertz-Mindlin(No Slip)模型，模型基于Hertzian和Middlin的理论：颗粒单元法向力和切向力都具有阻尼分量，阻尼系数和碰撞恢复系数具有一定的关系，切向摩擦力遵循库伦摩擦定律，滚动摩擦力通过接触独立定向恒转矩模型实现。

法向力满足式(4)。

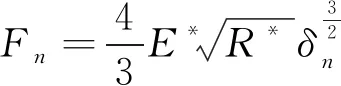
(4)

式中：E*为当量杨氏模量；R*为当量半径；δn为法向重叠量。

切向力满足式(5)。

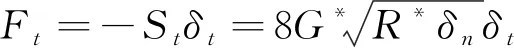
(5)

式中：St为切向刚度；G*为当量剪切模量；δt为切向重叠量。

滚动摩擦力满足式(6)。

τi=-μrFnRiωi

(6)

式中：μr为滚动摩擦系数；Ri为接触点到质心的距离；ωi为接触点处的单位角速度矢量。

3.2 试验材料参数获取

1) 材料本征参数。本次试验中使用的钢材为Q235钢，试验中的矸石本征参数通过三轴液压伺服试验机对岩石标准试件加载试验获得，矸石和钢材的本征参数见表2。

表2 试验材料本征参数表Table 2 The intrinsic parameters of experiment materials

2) 接触参数获取。使用离散元法进行数值模拟试验时，接触参数的准确性直接决定了数值模拟试验结果的准确性[14-15]。本实验通过使用圆筒式法测量矸石自然安息角获得接触参数[16]，当室内物理试验的安息角和数值模拟的安息角相等时，接触参数可用于数值模拟试验[17-18]。使用直径120 mm、高200 mm的钢桶，随机在煤矸石堆中铲取矸石物料，倒入钢桶中。将钢筒平稳放于铺有薄纸的平台上，缓慢竖向抬起钢桶，使得煤矸石物料从钢桶的底部缓慢放出，待煤矸石散落稳定后开始测定矸石物料的自然安息角，试验过程如图4所示。

图4 实验室安息角的测定Fig.4 Experimental of the rest angle

重复做3组试验，每次试验随机选取三个不同方向测量矸石安息角，试验数据见表3。最终得出本次试验的矸石自然安息角角度为34.67°。

表3 实验室安息角测定结果Table 3 Experimental determination results of the rest angle

利用EDEM中自带的图形编辑器创建钢桶模型，钢桶模型的参数与实际钢桶尺寸相同，为直径120 mm、高200 mm。在钢桶模型的上方创建颗粒工厂用于生成矸石颗粒。生成的矸石颗粒级配与自然状态下的矸石散体粒径级配一致，各粒径中不同形状矸石颗粒数量分布遵循统计结果，仿真中矸石颗粒全部为随机生成，可以视作最终生成的颗粒已经搅拌均匀。钢桶内生成矸石颗粒完成之后，静置0.5 s，使矸石颗粒间由于坠落产生的碰撞挤压停止。在0.5 s后，使钢桶以0.01 m/s的速度匀速竖直向上运行，使矸石颗粒从圆筒底部泻出形成安息角。仿真结果如图5所示。使用EDEM后处理中的Protractor功能对仿真的矸石安息角进行测量，最终实验结果见表4。

表4 仿真安息角测定结果Table 4 Simulation experimental determination results of the rest angle

图5 圆筒式仿真模型Fig.5 Simulation model of cylinder

实验室试验结果与仿真结果的相对误差见式(7)。

(7)

式中：ER为相对误差；Ea为绝对误差，是分析结果与数次平行测定结果的算术平均值之差；T为真值。

经计算求得相对误差ER为1.1%，远小于5%的误差允许范围，故数值仿真中矸石的接触参数符合要求，接触参数见表5。

表5 试验材料的接触参数表Table 5 The contact parameters of experiment materials

3.3 数值模拟结果与分析

按照实验室物理试验装置的尺寸和各部位间的位置关系建立的本次模拟的试验装置模型，简化的试验装置模型由直径120 mm、高200 mm的无盖钢桶和直径120 mm的压实板组成。试验中矸石颗粒模型与上文参数校准试验中的颗粒形状完全相同，直接采用上述的颗粒模型继续运算。试验装置与试验材料的本征参数见表2，接触参数采用圆筒法测量安息角校准后的参数见表5。按照泰波系数n取0.3～0.7时的粒径级配占比，各粒径中不同形状的矸石颗粒数量分布严格遵循统计结果，在钢桶模型中生成2 kg不同级配的矸石散体。然后使用压实板对不同级配的矸石散体进行压缩试验，压实板加载方式与实验室物理试验一致，采用位移加载方式，加载速率为0.001 m/s。试验结果如图6所示。

图6 数值模拟应力应变曲线图Fig.6 Stress-strain curves of numerical simulation of continuously-graded gangue

对图6数值模拟应力应变曲线进行分析可知。

1) 应力位于0～1.8 MPa阶段，泰波系数n取0.3和0.4时，两者的应变基本未发生变化，而泰波系数较大的试验中应变迅速增加，是由于泰波系数较小时，粒径为20～30 mm、30～40 mm的矸石颗粒较少，自然混合情况下矸石颗粒间结合紧密、孔隙较少，说明大颗粒少的情况下连续级配矸石散体密实度较高，需要更大的应力才能使矸石散体进一步密实。

2) 当应力为10 MPa，n取0.3和0.4时矸石散体的应变基本相等，约等于0.14，但随着n取值的增大，应变逐步降低至0.19，可以看出矸石散体在同一应力条件下应变随着n值的增大呈现先降低、后增高的变化规律，拐点为n取0.4时。说明粒径大的矸石颗粒在矸石散体中起到了一定支撑作用，但是随着大粒径矸石颗粒比例的提高，矸石颗粒间的孔隙率也逐步增大，严重影响矸石散体的密实度。

3)n取0.4时的连续级配矸石散体应力应变曲线斜率变化最小，说明该条件下的连续级配矸石散体压缩率最小，密实度最高，可作为现场充填级配参考。连续级配矸石压缩应力应变曲线由快速增加到缓慢增加的拐点应力均约为3 MPa，此后随着应力的增大应变增加幅度甚微。

4) 由图2与图6对比可知，数值模拟试验中泰波系数n取0.4时试件的最终压缩形变最小，最小应变为0.14，n取0.7时试件的最终压缩形变最大，最大应变为0.19；实验室物理试验中n取0.4时试件的最终压缩形变最小，最小应变为0.23，n取0.6时试件的最终压缩形变最大，最大应变为0.27。可见，物理试验与数值模拟试验相同条件下最终应变存在0.1的误差，主要原因在于：实验室中，矸石在压缩过程中，当达到一定的压力时，矸石颗粒间已经达到极限平衡，进一步压实，将引起大颗粒矸石发生破碎，导致最终变形较大。总体上仿真结果基本符合实验室压缩的趋势，且泰波系数取0.4的矸石颗粒级配是最优级配。

4 结 论

1) 使用圆筒式安息角测量法，对矸石物料进行了安息角实验测定，验证了EDEM对应参数下数值模拟结果的准确性，表明测得的矸石本征参数与接触参数是可靠的，这为以后物料参数的标定提供了一定的理论基础。

2) 实验室连续级配矸石压缩应力应变曲线和仿真级配矸石应力应变曲线形态接近，应变随应力增大呈先快速增加后逐渐变缓的趋势，拐点约为3 MPa，泰波系数n=0.4的连续级配矸石，在所有泰波系数级配压缩试验中密实度最大，可以为现场试验作为参考。

3) 实验证明，EDEM离散元仿真是一种有效的验证和获取矸石最优配比、密实度等宏观参数的方法，可用于实际生产快速寻找合适的矸石级配。