基于谐响应分析的燃机压气机动叶片尾流激振响应预估方法

杨博宇 张 玲 文丰艾 文丰茜

(1.东方电气集团东方汽轮机有限公司产品研发中心，四川618000；2.二重(德阳)重型装备有限公司，四川618000；3.中国科学院光电技术研究所，四川610000；4.西南技术物理研究院，四川610000)

燃机轴流式压气机在正常工况下稳定运转时，因为附面层以及叶片尾缘对空气流场的影响，会导致静叶栅出口处的空气流动速度出现亏损，如图1所示。近年来轴流式压气机设计不断紧凑化，使压气机各级静叶栅、动叶栅之间的轴向间距非常小，导致压气机静叶栅出口处的空气流速亏损在其分布的流场空间中来不及复原，最终产生明显的流场周向畸变[1]。

图1 压气机静叶栅尾流示意图Figure 1 Wake flow of compressor static cascade

1 叶片在非定常周期下的分析

如果不考虑静叶栅叶片在生产加工以及装配过程中产生的各种误差，即认为静叶栅是理想均匀分布的，那么由静叶栅尾流导致并施加于本级动叶片的激振力是以叶轮转角为自变量的周期函数[2]，叶轮每转过一个静叶栅节距所对应的圆心角，动叶片上各点的激振应力便循环变化一次。设K为组成静叶栅的叶片总数，那么叶轮每旋转一周，每支动叶片将受到K次循环变化的尾流激振作用。

显然，此时动叶片表面的非定常周期激振力在一个周期区间内只有有限个第一类间断点和极值点，即满足狄利克雷收敛定理，可以进行傅里叶级数展开，分解为定常激振力和各阶谐振力，即：

(1)

式中，F为尾流激振力；F0为定常激振力；Fj为第j阶谐振力幅值；φj为第j阶谐振力相位角；K为静叶栅叶片数；ω为压气机转子角频率。

此外，为方便后续表述，令各阶谐振力的圆频率为Ω，即：

Ω=jKω(j=1，2，3…)

(2)

将定常激振力和各阶谐振力分别作用于动叶片表面时所产生的响应进行线性叠加，即可求得静叶栅尾流场引起的本级动叶片激振所产生的总响应。

以上分析仅针对轴流式压气机静叶栅为理想均匀分布的情况，仅讨论在此种情况下动叶片叶身局部微面承受尾流激振力时动叶片模型响应的预估方法，并给出动叶片模型在均匀静叶栅尾流场中承受尾流激振力时产生响应的求解方法。

2 压气机动叶片简谐激振的响应分析

将动叶片所承受的尾流激振力分解为定常激振力和各阶谐振力后，可以计算动叶片在各阶谐振力作用下的响应值。

将动叶片视为多自由度振动模型，并考虑弱阻尼的影响，列出其在简谐载荷作用下的受迫振动微分方程[3-4]：

(3)

使用正则振型矩阵[AN]对公式(3)进行解耦，令

{X}=[AN]{XN}

(4)

式中，{X}为原物理坐标系下振动模型的响应；{XN}为正则坐标系下振动模型的响应。

(5)

将公式(4)代入公式(3)，等号两边再同时乘正则振型矩阵的转置[AN]T，得：

+[AN]T[K][AN]{XN(t)}=[AN]T{F}sin(Ωt)

(6)

考虑到刚度矩阵[K]、质量矩阵[M]为半正定或正定的对称阵，以及正则振型矩阵[AN]的正交性，得出：[MN]=[AN]T[M][AN]=[I]，即正则质量矩阵[MN]为单位阵；[RN]=[AN]T[R][AN]，这里采用比例阻尼假设，则[RN]为对角阵；[KN]=[AN]T[K][AN]，[KN]为对角阵，其对角线元素为各阶固有频率值的平方。

则公式(6)化简为：

=[AN]T{F}sin(Ωt)

(7)

再令 {FN}=[AN]T{F}

(8)

式中，{FN}为广义激振力幅值列阵。

由于公式(7)已经解耦，将公式(8)代入公式(7)，并将矩阵方程写成分量的形式，即得：

(i=1,2,3,…,n)

(9)

式中，α，β为与比例阻尼有关的系数；fNi为{FN}的第i个元素；ωni为动叶片振动模型的第i阶固有频率。

采用求解单自由度振动模型响应的方法计算公式(9)，即可求得动叶片多自由度有阻尼振动模型在简谐载荷作用下于正则坐标系下的稳态响应，即：

(10)

式中，βi为放大因子；ψi为相位角。

再由公式(4)将正则坐标系下的稳态响应值转换回原物理坐标系，即：

(11)

至此，完成压气机动叶片多自由度有阻尼振动模型在简谐激励作用下的稳态响应理论分析求解。

3 动叶片尾流激振响应预估

3.1 激振应力周期延拓及傅氏级数拟合

已知压气机转子每转过一个静叶栅节距所对应的圆心角时，动叶片某型线T1压力面测点A尾流激振应力的变化情况[5]。静叶栅由50支叶片组成，压气机转子旋转一周时，此激振应力将循环50次，使用MATLAB软件对测点A的尾流激振应力函数进行周期延拓，初始时刻的时间设置为零，并使用7阶傅里叶级数对测量离散点进行拟合，得到测点A尾流激振应力载荷谱如图2所示，这里拓展至16个周期。

图2 动叶片T1型线测点A尾流激振应力载荷谱Figure 2 Wake flow vibration stress loading spectrum of dynamic blade T1 shaped line measuring point A

T1型线A点各测量离散值周期延拓后使用7阶傅里叶级数拟合的相关参数见表1，其函数表达式为：

(12)

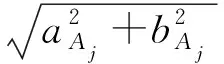
表1 A点各测量离散值使用7阶傅里叶级数拟合的相关参数Table 1 Related parameters of measuring discrete valueson point A by using 7 phase Fourier series fitting

图3 建立动叶片压力面侧的投影面SFigure 3 Projective plane S setting of dynamic blade pressure plane side

图4 投影面S施加各阶谐振力Figure 4 Projective plane S loaded with various phase harmonic vibration force

表1中的R-square即可决定系数，是统计学中用于度量拟合优度的一个参数，用于表现拟合模型中自变量因变量变动百分数的程度，其取值范围是[0～1]，且取值越大该模型拟合优度越佳[6]。动叶片T1型线A点各测量离散值使用7阶傅里叶级数拟合，其可确定系数为1，显然取得很好的拟合效果。此外，低阶谐振力对压气机叶片动态特性的影响远高于高阶谐振力，因此使用测点A的前几阶谐振力对叶片的动态特性进行仿真，能很好地接近其真实的响应状态。

3.2 局部激振力加载及动叶片的响应预估

先计算动叶片T1型线测点A承受各阶谐振力时动叶片的响应。由于A点的测量结果为压应力值，即力学概念中的压强，而ANSYS Workbench谐响应分析中的压力分布载荷只能使用默认的零值初相角，显然与表1中各阶谐振力的初相角不相符。

为了保证测点A的各阶谐振力按照真实情况进行加载，首先在A点的切平面上以A点为几何形心，做一个长、宽皆为5 mm的矩形，将此矩形沿切平面法向拉伸5 mm，成一立方体。再使用“投影工具”命令将立方体向动叶片压力面投影，获得曲面S，见图3，事实上，只要曲面S的面积足够小，则可近似认为S上各点的谐振力幅值和初相角相等[7]。设曲面S的面积为C，即C≈25 mm2，则曲面S承受的各阶谐振力可表述为：

(j=1,2,3,…,7)

(13)

且各阶谐振力方向为沿曲面S的法向，如图4所示。计算投影面S承受一阶谐振力时动叶片的响应为：

(14)

进入ANSYS Workbench谐响应分析环境，首先抑制为获得投影面S而建立的立方体，再对动叶片进行单元网格划分，参考公式(14)和表1一阶谐振力等相关数据设置待求解频率域、待求解频率间隔、简谐载荷幅值和初相角。注意在ANSYS Workbench谐响应分析设置中使用的物理量是频率，单位是Hz，而非理论分析中经常使用的以rads为单位的圆频率或角频率，频率和圆频率相差2π倍，因此需要对公式(14)中的圆频率值做相应的转化处理。参考公式(13)和表1中第二阶至第七阶谐振力的相关数据，计算动叶片有限元模型在指定载荷频率和初相角情况下的响应值，如图5所示。

(a)一阶谐振力,等效应力(b)一阶谐振力,总变形(c)二阶谐振力,等效应力(d)二阶谐振力,总变形(e)三阶谐振力,等效应力(f)三阶谐振力,总变形(g)四阶谐振力,等效应力(h)四阶谐振力,总变形(i)五阶谐振力,等效应力(j)五阶谐振力,总变形(k)六阶谐振力,等效应力(l)六阶谐振力,总变形(m)七阶谐振力,等效应力(n)七阶谐振力,总变形

由图5可知投影面S承受各阶谐振力作用时动叶片模型各阶的等效应力极值和总变形极值，其分布情况如图6(a)和图6(b)所示，可以看出一阶谐振力引发的响应极值远高于其余各阶，一阶等效应力极值达二阶的23倍，一阶总变形极值更是达到了二阶的32倍，由此可见，仅取前几阶低阶谐振力进行叶片的动力学仿真是可以满足工程需要的。

(a)(b)

(a)等效应力(b)总变形

其次，计算投影面S承受定常激振力时动叶片模型的响应。此时，S面内分布的定常激振力为：

FS0=σA0C

(15)

将表1中相关数据代入公式(15)，计算投影面S承受定常激振力作用时动叶片模型的等效应力和总变形，如图7(a)和图7(b)所示。

由于压气机动叶片尾流激振的响应分析是采用公式(3)偏微分矩阵方程进行的，该方程满足线性叠加原理，即如果{X1(t)}和{X2(t)}分别是动叶片模型在两个不同的激振力作用下的响应，那么它们的线性组合即{X1(t)+X2(t)}就是动叶片模型在这两个激振力共同作用下的响应。

因此，将投影面S承受各阶谐振力和定常激振力时动叶片的等效应力进行线性叠加，即将图5以及图7的等效应力分布进行线性叠加，即可求得投影面S承受尾流激振力时动叶片模型的等效应力分布。类似地可求得投影面S承受尾流激振力时动叶片模型的总变形。

3.3 动叶片尾流激振响应计算方法

整个动叶片在均匀静叶栅尾流场中承受尾流激振力时产生的响应问题，也可按上述方法计算：

(1)在动叶片叶身表面覆盖一层曲面，参考叶身表面各测点的几何位置对该曲面进行面网格单元划分，例如以叶身表面各测点的坐标作为面单元的形心坐标进行面网格单元的划分。面网格单元划分得越细，计算效果越佳。

(2)使用计算局部微面S承受尾流激振力时动叶片模型响应的方法，分别计算各面单元承受尾流激振力时动叶片的响应。

(3)由于计算采用偏微分矩阵方程进行，仍符合线性叠加原理，因此将第二步中各面单元受力产生的响应进行叠加，即可求出动叶片在均匀静叶栅尾流场中承受尾流激振力时产生的总响应。

4 结语

通过研究燃机压气机均匀静叶栅尾流对下游动叶片产生的影响，用傅里叶级数将周期激振力展开为定常项和各阶谐振力，分析了各阶谐振力作用下燃机压气机动叶片多自由度有阻尼振动模型的稳态响应，以及将各阶谐振力与定常激振力作用下的响应线性叠加求解总响应的计算方法。此方法便于对压气机动叶片尾流激振响应进行有效预估，具有一定的工程应用价值。