基于内聚力模型的一维弹塑性复合金属材料有限元断裂分析

李乐毅

(四川建筑职业技术学院机电与信息工程系，四川618000)

随着智能模拟软件的高速发展，模拟材料断裂的萌生、扩展和最终分离的整个变化过程需要高精度的模拟软件和解析方法，其中，目前一个重要研究发展方向是如何利用现有的商用有限元软件来准确高效地模拟材料的裂纹扩展。金属，尤其是弹塑性复合金属材料的裂纹萌生、扩展和最终分离是一个强非线性过程，传统的有限元解析方法很难有效地模拟弹塑性复合金属材料的裂纹萌生、扩展和最终分离引起的动态响应应力与位移扩展的不连续性[1-4]。

近十年来，为了专门克服弹塑性复合金属材料的裂纹变化过程所遇到的困难，许多专家学者提出了许多解析方法，例如改良边界元法、离散有限元法和虚拟节点法等[5-6]。上述理论都可以在一定范围内有效地模拟弹塑性复合金属材料裂纹的扩展，但通用性和运用范围受限，对于裂纹扩展复杂的弹塑性复合金属材料，在模拟时耗时较长或模拟结果发散。近几年，有专家学者提出了一种基于内聚力模型的有限元算法，该算法无需预先设置附加节点或约束就能处理弹性材料的裂纹发生、扩展和最终分离，由于基于内聚力模型的有限元算法具有精度高、稳定性好、耗时短等优点，表现出广阔的应用前景。但是，该方法尚未应用在弹塑性复合金属材料。

因此，在现有研究结论的基础上，针对一维弹塑性复合金属材料的断裂问题，以一维二节点杆单元为研究模拟对象，提出一种基于内聚力模型的一维弹塑性复合金属材料有限元模拟方法，并把该方法嵌入传统有限元软件Abaqus中进行有限元分析。

图1 一维弹塑性杆单轴加载Figure 1 One dimensional elastic-plastic rod uniaxial loading

1 基于内聚力模型的有限元法

图1是对一维弹塑性复合金属材料杆进行双向加载，用Ω代表完整的弹塑性复合金属材料杆，杆长为l，横截面积为A，当弹塑性复合金属材料杆承受双向加载时，杆件下部节点1的位移量为u1，节点受力为F1；杆件上部节点2的位移量为u2，节点受力为F2。所以，在竖直x轴方向产生的净位移量为u=u2-u1。

(1)

等向强化函数为：

(2)

其中p为节点处应变。采用米塞斯屈服强度准则进一步判断当前时刻弹塑性复合金属材料杆的弹塑性状态，屈服函数为：

f=σ-r-σy

(3)

当f<0时，复合金属材料杆发生弹性变形，满足Dep=E；当f=0时，复合金属材料杆发生弹塑性变形，满足Dep=Eh(E+h)，其中Dep为材料切线刚度矩阵。

图2 三角形内聚力关系Figure 2 Triangle cohesion relationship

弹塑性复合金属材料杆的非线性断裂过程选用如图2所示的三角形内聚力模型进行模拟，数学上可表示为：

(4)

在公式中引入上标i∈[1，2，3，4]代表内聚力关系段号，其中，内聚力关系第i段的斜率用α(i)表示，所以，公式(4)中应力σ余裂纹张开位移δn的关系式可以改写为：

(5)

(6)

而且内聚力关系斜率α(i)可以表示为：

(7)

与此同时，复合金属材料杆的裂纹张开位移δn的取值范围可以表示为：

(8)

在上述内聚应力模型中，复合金属材料杆的裂纹张开度δn对应的能量释放率G可以表示为：

(9)

复合金属材料杆的断裂准则可以改写为：

G=Γc

(10)

其中Гc为复合金属材料杆的断裂韧性。

2 基于内聚力模型的有限元模拟测试

如图3所示，为弹塑性复合金属材料一维二节点杆有限元模拟拉伸测试的几何模型，同时采用两种模式进行加载，一种是当复合金属材料杆单元进入塑性变形阶段后马上进行卸载，再重新加载直到复合金属材料杆完全断裂，另一种是当复合金属材料杆单元进入内聚力裂纹扩展阶段后马上进行卸载，再重新加载直到复合金属材料杆完全断裂，选用上述两种循环加载情况进行单元测试。

图3 一维二节点弹塑杆单元Figure 3 One dimensional two nodes elastic-plastic rod unit

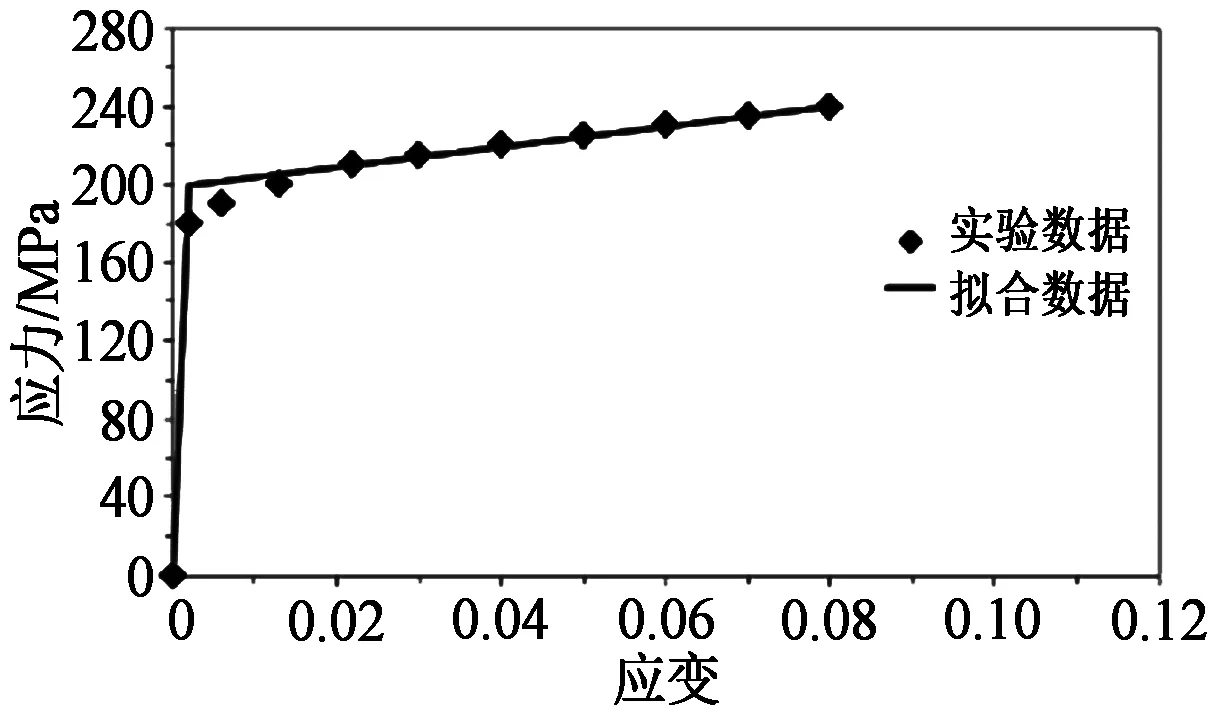
图4 应力-应变曲线及其拟合结果Figure 4 Stress-strain curve and fitting result

首先，采用当复合金属材料杆单元进入塑性变形阶段后立即卸载，再重新加载到复合金属材料杆完全断裂的模拟方案进行测试。即控制外加载荷位移从u=0加载到u=1.2 mm，复合金属材料杆单元进入塑性变形阶段，接着卸载到u=1.0909 mm时，外加载荷变为0，最后再加载到u=3.6 mm时，杆件完全断裂。如图5所示给出了在整个加载过程中弹塑性复合金属材料杆的应力-应变关系数值解(FEM)与实验数据(experimental)、线性拟合结果(fitting curve)以及解析解(analytical solution)之间的对比，由图5可知，上述四种结果基本一致，验证了基于内聚力模型的一维弹塑性复合金属材料有限元模拟方法在分析一维杆件进入塑性变形段卸载后再加载到完全断裂时的准确性。

图5 加载点应力-应变曲线Figure 5 Stress-strain curves of loading points

然后采用当复合金属材料杆单元进入内聚力裂纹扩展阶段后立即卸载，再重新加载直到复合金属材料杆完全断裂的模拟方案进行测试。即控制位移从u=0加载到u=2.4 mm，复合金属材料杆单元进入内聚力裂纹扩展阶段，接着卸载到u=2.28 mm时外力为0，最后再加载到u=3.6 mm时完全断裂。图6给出了整个加载过程中应力-应变关系的四种结果对比，其结果也基本一致，验证了基于内聚力模型的一维弹塑性复合金属材料有限元模拟方法在模拟一维杆件进入内聚力裂纹扩展阶段卸载后再加载到完全断裂整个加载过程时的准确性。

图6 加载点应力-应变曲线Figure 6 Stress-stain curves of loading points

3 结论

针对弹塑性复合金属材料的断裂问题，以一维二节点杆为研究对象，提出一种基于内聚力模型的有限元算法，并借助有限元软件Abaqus，以一维弹塑性复合金属材料杆单轴拉伸为实验背景，对两种循环加载过程进行了有限元模拟，通过与实验数据、线性拟合结果以及解析进行对比，验证了基于内聚力模型的一维弹塑性复合金属材料有限元模拟方法的精确性。