梁拱组合体系桥梁空间效应与关键构造设计方法研究

薛玉波,余 郁,熊 文,叶见曙

(1. 扬州市市政建设处, 江苏 扬州 225000; 2. 东南大学 交通学院 桥梁工程系, 江苏 南京 210096)

0 引言

梁拱组合体系桥梁是在传统刚架拱桥的基础上做了优化设计。通过对上部主梁和拱圈(肋)施加预应力，从而取消空腹部分的立柱及斜撑，使得整个结构显得更加轻巧、美观。从拱的意义来说，梁拱组合体系桥梁拱上建筑的构件已减至极限，仅剩下水平桥面系，外形也简洁至极限，并接近斜腿刚架。事实上，此种桥型与斜腿刚架已无本质区别，只不过将斜腿刚架的斜腿转换为拱轴曲线。显然，其受力条件比斜腿刚架更加优越，因为经过优化设计的曲线拱腿压力线会比直线形斜腿更接近于形心轴线[1-3]。

由于市政桥梁越来越宽，在满足通行需求的同时还要兼顾美观的效果，使得城市桥梁的结构形式更加复杂。当梁拱组合体系桥梁应用于城市中，仍存在以下主要设计难点[1-2]。①城市宽体梁拱组合体系桥梁的空间受力特性对施工以及运营阶段的力学影响；②施工阶段梁拱结构体系转化时的力学分析;③梁拱组合体系空腹三角区域的关键设计参数分析。这些设计难题也部分限制了该类桥型在市政桥梁中的应用与推广。

本文以扬州市观潮路跨古运河大桥(宽体梁拱组合体系桥梁)为工程背景，利用大型通用有限元程序ANSYS建立三维实体单元模型，对该桥的施工体系转化过程进行精细化数值模拟，重点分析其空间结构受力特征。通过改变关键设计参数取值(包括宽跨比、截面形式、横向连接方式等)，利用参数分析手段对该桥运营阶段的空间力学效应进行分析，明确各参数与空间效应之间的关联。针对梁拱组合体系桥梁的关键构造空腹三角区域，提出拱梁刚度比的设计参数指标，得到该指标对结构空间受力的影响。研究结果为梁拱组合体系桥梁的结构安全性与设计合理性提出了更明确的理论解释与优化依据。

1 背景桥梁简介

观潮路跨古运河大桥上部结构为上承式预应力混凝土梁拱组合体系，桥梁全长144 m，跨径布置为(38+68+38)m,见图1。横向设计为双向四车道，桥宽30 m，采用单幅桥结构，横向布置为2 m(人行道)+4 m(非机动车道)+1.5 m(侧分带)+15 m(机动车道)+1.5 m(侧分带)+4 m(非机动车道)+2 m(人行道)。

图1 桥梁立面图(单位：cm)Figure 1 Vertical view of bridge (Unit: cm)

该桥主梁采用变截面预应力混凝土连续箱梁，单箱六室截面，箱梁顶板宽30 m。中跨跨中、墩顶端及边跨梁端中心线处梁高2 m，高跨比为1/34，箱梁与拱圈相交处梁高主跨侧4.121 m，边跨侧4.098 m，箱梁高度据拱圈线形按圆弧变化。主墩两侧各设置一半拱，拱圈采用等厚度钢筋混凝土板拱，拱轴线采用圆弧线，中跨和边跨拱轴线半径分别为51.625、51.987 m，矢高分别为6.599、5.708 m，矢跨比分别为1∶7.576、1∶8.765。拱圈厚1.2 m，底宽25 m，顶宽20 m，与箱梁相交处拱圈顶宽根据造型需要变化。拱圈与箱梁及桥墩拱座固结，形成刚构体系,见图2。

图2 主梁典型断面图(单位：cm)Figure 2 Typical cross-section of the bridge (Unit: cm)

该桥道路等级为城市次干路，设计速度为40 km/h，设计荷载等级城-A级，人群荷载取3.645 kPa/m2，非机动车道荷载按照《城市桥梁设计规范》(CJJ 11-2011)相关条文取值；二期恒载按7 cm混凝土调平层及10 cm沥青铺装层设计，并考虑绿化带及人行道，共计175 kN/m；结构整体升降温按25 ℃计入。桥梁设计基准期为100 a，设计安全等级为一级，结构重要性系数取1.1。

2 数值模型

2.1 模型建立

该桥空间结构较为复杂，为使模型更接近真实受力状况，准确分析空腹式梁拱组合桥的施工过程，本文采用基于ANSYS通用有限元软件的三维实体有限元模型进行模拟[4-5]。主梁、拱圈和拱座均采用Solid65实体单元，预应力筋采用Link8单元；拱座底部完全固结，桥台处按10 m间隔设置3个支座，中间支座约束横桥向与竖向位移，两侧支座只约束竖向位移；施工过程中张拉预应力可能导致梁体“脱架”，因此支架采用Combin39单元，以实现单向受压支架的模拟。

主梁采用变截面预应力混凝土连续箱梁，模型左跨各断面如图3所示。由图3可知，箱梁顶、底板厚度、腹板厚度及截面高度均发生不断改变，由于纵坡的原因，顶板位置也在不断变化。

(a) 端支座处

(b) 边跨侧

(c) 中跨侧

(d) 最大梁高处

出于美观考虑，箱梁边腹板倾斜，除墩顶段外，箱梁下缘根据造型需要设置向上斜面，斜面与边腹板间设置圆倒角，斜面的斜率与圆倒角半径随之发生不规律的变化。有限元模型中该圆弧段变化采用五节段线性变化代替[6]，如图4所示。

图4 主梁变化段有限元模型

拱圈上部箱梁施工时支架无法支撑在拱圈上，故拱圈开孔，设置4排钢管桩分别从孔中穿过，另外一排放置在墩顶。钢管桩上放置H型钢盖梁，盖梁上纵向铺设工字钢，工字钢上放置木方及模板。该拱圈与主梁形成的空腹三角区域及挖孔构造的有限元模型如图5所示。

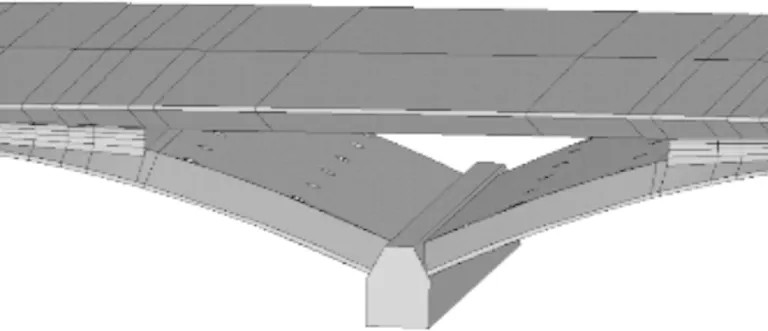
图5 梁拱三角区域有限元模型

预应力筋和混凝土分别采用不同单元模拟，并将预应力筋节点与邻近混凝土节点耦合，从而将力筋单元和实体单元联系起来，并通过降温法施加预应力[7]。降温幅度计算公式为：

(1)

式中：ΔT为施加的降温值；F为预拉力值；E为钢束弹性模量；A为钢束截面面积；σ为预应力值；α为钢材线膨胀系数，1.2×10-5/℃。全桥预应力有限元模型如图6所示。

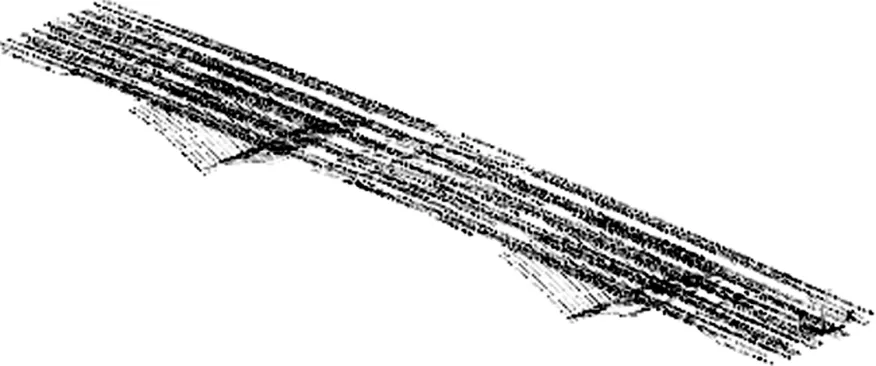
图6 预应力有限元模型Figure 6 Finite element model of the pre-stressed steel bars

该桥施工方法与步骤为：①浇筑下部及拱圈；②支架现浇墩顶箱梁段及中横梁段；③支架现浇悬臂段；④支架现浇边跨合拢段及中跨悬臂段；⑤中跨合拢成桥，拆除支架，施工桥面铺装、绿化带及人行道。利用ANSYS单元生死功能对施工阶段进行数值模拟，各施工阶段如图7所示。

(a) 施工阶段1

(b) 施工阶段2-3

(c) 施工阶段4

(d) 施工阶段5

混凝土单元网格划分尺寸为0.4 m，全桥共974 872个混凝土单元；预应力钢束单元网格划分尺寸为0.5 m，全桥共20 280个预应力单元。

2.2 模型对比

同时采用杆系有限元软件MIDAS建立杆系模型，将该模型的计算结果与ANSYS建立的精细化空间模型计算结果进行对比。两种计算软件得到的各主要施工阶段支座反力数值如表1所示。

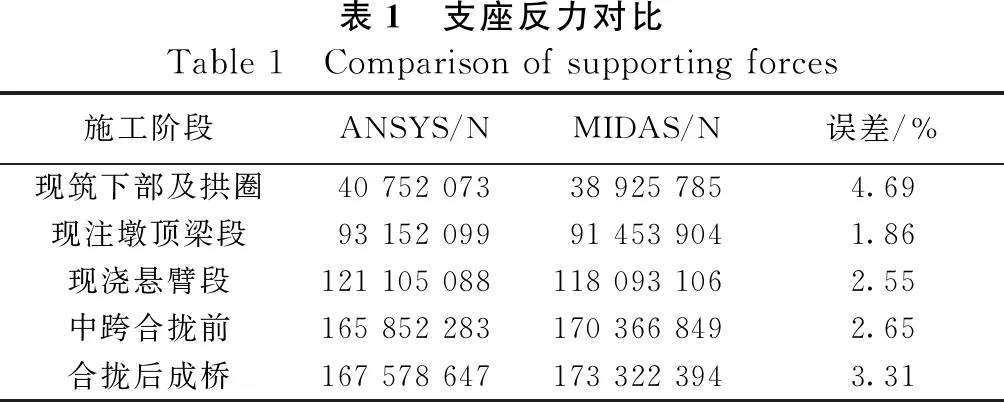
表1 支座反力对比Table 1 Comparison of supporting forces施工阶段ANSYS/NMIDAS/N误差/%现筑下部及拱圈40 752 07338 925 7854.69现注墩顶梁段93 152 09991 453 9041.86现浇悬臂段121 105 088118 093 1062.55中跨合拢前165 852 283170 366 8492.65合拢后成桥167 578 647173 322 3943.31

由表1可知，ANSYS与MIDAS软件得到几乎一致的支座反力，实现了两者结构形式与材料属性建模准确性的互校。但由于ANSYS模型可准确考虑横纵坡、横隔板、拱圈挖孔、拱座等构件局部形态，而MIDAS模型对此均无法准确建模，故两者支座反力计算结果仍具有一定差异，但均在5%范围以内。

对于施工阶段模拟，ANSYS与MIDAS模型计算得到的挠度变化趋势均一致(见图8)，但具体数值有所差异。例如，中跨合拢前，由于边跨已合拢，整体变形不大，中跨仍处于悬臂状态，故张拉预应力使得悬臂端翘起明显；此时MIDAS模型最大挠度为31 mm，而ANSYS模型为20 mm。合拢成桥后，MIDAS模型最大挠度为38 mm，而ANSYS模型最大位移为22 mm。可以看出，两者模型由于单元类型不同导致结构建模的准确程度不同，局部构件的刚度模拟上也会有所不同。由于ANSYS为实体建模，可完整计入空间各方向的结构刚度，显然空间挠度分析的结果更加准确[8-9]。

(a) ANSYS模型

(b) MIDAS模型

另外，由于ANSYS模型分析得到的应力为空间分布，而MIDAS仅能得到平截面假定下的平均应力，所以并不具有可比性(见图9)。显然，ANSYS的分析结果更能体现出梁拱组合体系桥的空间受力特点以及应力空间分布。

(a) ANSYS模型

综上可知，通过与MIDAS模型计算结果的对比，ANSYS模型荷载效应模拟准确，能够得到与实际结构形式更为相符的空间力学效应与分布，即采用更为精细的实体三维空间模型进行宽体梁拱组合体系桥梁的模拟分析是非常必要的。

3 空间受力特征分析

3.1 施工阶段空间分析

a.纵向正应力沿桥纵向分布。

各施工阶段主梁顶板中点纵向正应力σz沿桥纵向分布如图10所示，其中正值代表拉应力，负值代表压应力(下同)。由图10可知，各施工阶段(施工阶段1尚未施工主梁)顶板中间位置均受压。施工阶段2-3最大压应力仅为3.5 MPa，施工阶段4-5压应力主要范围为4～10 MPa，最大达到13 MPa，均小于C50混凝土的设计强度。

图10 纵向正应力沿纵桥向分布Figure 10 Distribution of longitudinal stress along the longitudinal direction of the bridge

b.纵向正应力沿桥宽分布。

考虑到拱梁结合部位构造复杂、空腹区域系梁的体系转换以及边、中跨不同的受力特点，所提取纵向正应力沿桥宽分布的控制截面如图11所示。

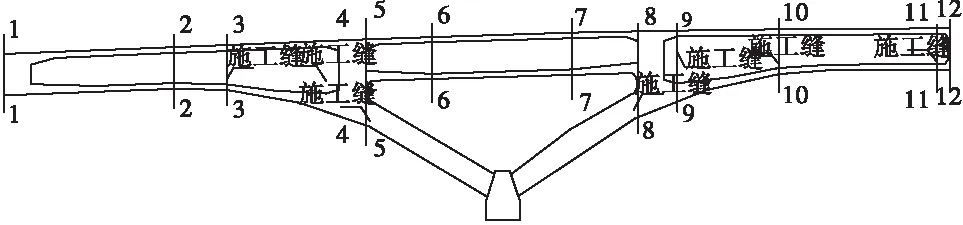
图11 控制截面Figure 11 Selected cross-sections

各施工阶段在自重和预应力作用下典型控制截面顶、底板的纵向应力沿梁宽方向的分布规律如图12、图13所示。其中横坐标表示相对横向位置(顶板：-15～15 m，底板：-12.5～12.5 m)，纵坐标表示纵向应力数值。

(a) 4-4截面

(b) 6-6截面

(c) 8-8截面

(d) 10-10截面

(a) 4-4截面

(b) 6-6截面

(c) 8-8截面

(d) 10-10截面

由图12可知，施工阶段2中梁拱三角区域端部截面的顶板正应力接近均匀分布；而梁拱三角区域内部系梁截面的顶板正应力分布具有明显的空间分布特征，包括剪力滞效应。施工阶段3，接近梁拱三角区域端部的梁截面应力分布比较均匀；而三角区域内部的分布规律同施工阶段2。施工阶段4与5中，中跨梁段截面正应力会发生明显波动，空间效应明显，数值也较前序施工阶段增大，最大压应力可达10 MPa。

由图13可知，施工阶段2中梁拱三角区域端部截面出现应力波动，但变化范围控制在-1～0.2 MPa；其它截面呈中间大、两边小并兼有剪力滞效应的应力分布特征。施工阶段3除了中跨跨中附近，其它截面应力分布规律均类似阶段2，但应力略有增加。施工阶段4完成边跨合拢，阶段5完成中跨合拢，所以这两阶段边跨及梁拱三角区域系梁应力变化不大，合拢后原本处于悬臂状态的中跨压应力有所增大。

c.横向正应力沿桥宽分布。

通过计算分析可以发现，无论是截面顶板还是底板横向正应力，均有非常明显的空间分布特征。但需要说明的是，由于施工阶段1-3横向荷载较小，仅自重效应，所以主梁横向正应力沿桥宽的波动范围并不大。直到施工阶段4-5，边跨中跨合拢后，各截面应力有所增加，范围为-8～2 MPa。

3.2 运营阶段参数分析

a.宽跨比分析。

该桥设计宽度为B0=30 m，机动车道为双向四车道。分别改变桥宽至B1=33.75 m(五车道)、B2=37 m(六车道)以研究宽跨比对该类桥型的力学影响。截面形式仍为单箱六室，仅将横截面整体“拉宽”。考虑恒载、活载及温变作用，选取3个关键截面进行分析：中跨跨中截面、边跨与拱结合截面、中跨与拱结合截面。最不利弯矩布载下各截面纵向应力横向分布如图14所示(由于篇幅有限，此处仅给出中跨跨中截面的结果)。

由图14可知，随着宽度增加，平均压应力先略降低后增大(主要由于荷载也在变化)，变化幅度分别为-2.4%、7.08%，但应力分布规律始终一致。令λ为应力变化幅度与平均压应力之比，则B=30 m时，λ30=1.57；B=33.75 m时，λ33.75=1.61；B=37 m时，λ37=1.38。可以发现，随着桥宽增加，应力不均匀程度变化不明显。同理，对于边跨与拱结合截面，可得到λ30=7.86，λ33.75=2.85，λ37=2.34；对于中跨与拱结合截面，可得到λ30=1.04，λ33.75=1.87，λ37=2.20。可以看出，宽跨比对边梁与拱结合截面处的应力分布影响最大。

图14 宽跨比参数分析结果

Figure 14 Parametric study on the ratio of width to span length

b.截面形式分析。

顶底板厚度、腹板宽度不变，通过改变箱室宽度使得原设计单箱六室成为单箱五室截面。此处仅给出中跨跨中截面在最不利弯矩布置下的顶板纵向应力沿桥宽分布图(见图15)。

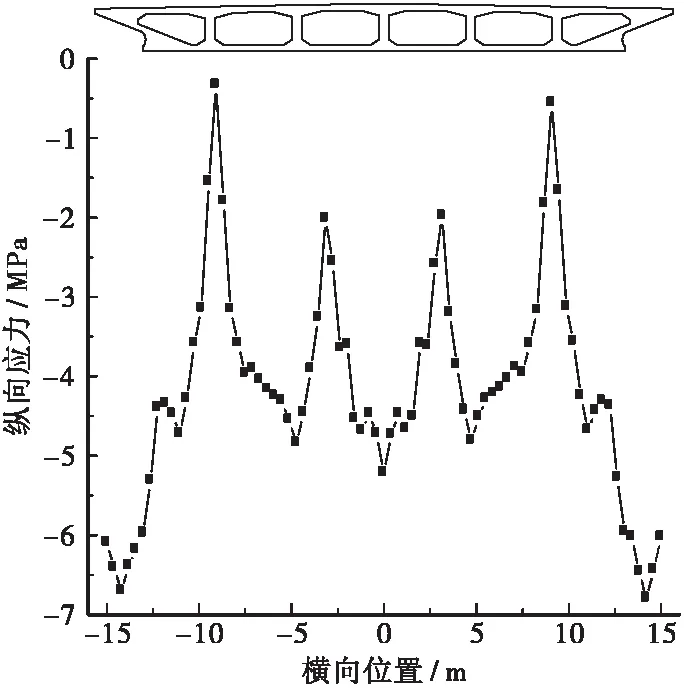
(a) 单箱6室

(b) 单箱5室

由图15可知，图15(a)中4个峰值与图15(b)中5个峰值位置恰好与单箱5室及单箱6室的腹板位置一致，说明纵向应力在桥宽方向的分布符合剪力滞效应，腹板近处较小，远处逐渐增大。其中，中跨跨中截面顶板以受压为主，单箱5室变成6室后，由于腹板数量增多，平均压应力降低3.5%。另外，5室变6室后，通过对比λ(应力变化幅度与平均压应力之比)的数值可以发现，纵向应力不均匀程度略微增加，但影响并不明显。

c.横向连接方式分析。

在单箱5室截面[见图15(b)]的基础上修改得到双箱双室截面，两箱间采用刚接或铰接，如图16所示。有限元模型中，两箱横向形成一个整体时，即为横向刚接；两箱横向在截面中点处弯曲变形“断开”，耦合两侧节点的平动位移时，即为横向铰接。

(a) 双箱横向刚接

(b) 双箱横向铰接

两种横向连接形式下的中跨跨中纵向应力沿桥宽分布如图16所示。由图16可知，横向铰接相对于刚接，由于整体性较差，纵向正应力偏大，顶板平均压应力增大26.2%，最大值增大8.3%。横向刚接纵向压应力最大5.3 MPa，位于悬臂端部附近；横向铰接纵向压应力最大5.8 MPa，同样位于悬臂端部附近。基于边梁与梁拱结合段位置的分析结果，横向铰接相对于刚接，顶板平均应力由0.08 MPa拉应力变为1.69 MPa压应力；横向刚接纵向压应力最大1.24 MPa，位于内侧腹板与顶板交界处；横向铰接纵向压应力最大5.43 MPa，位于中腹板与顶板交界处。综上可知，横向铰接虽可释放弯矩，降低局部弯曲应力，但由于整体性明显降低，反而使得整体应力水平提高，同时应力横向分布均匀性降低。

4 拱梁刚度比分析

梁拱组合体系桥梁由主梁和拱圈相互协作，共同承受荷载，充分发挥梁受弯、拱受压的受力特点及其组合作用。很显然，拱梁刚度比是影响梁拱组合体系桥梁结构受力分配的重要参数之一。

4.1 施工阶段影响分析

空腹区域梁拱组合结合部位的构造复杂，施工阶段需特别关注其受力，尤其是拱梁刚度比变化所带来的受力变化。本文通过在有限元模型中设置不同的梁拱刚度比数值，按图7给出施工方法分别计算对应的受力状态。由于合拢前结构状态最为不利，图17仅给出施工阶段4梁拱结合段计算结果。

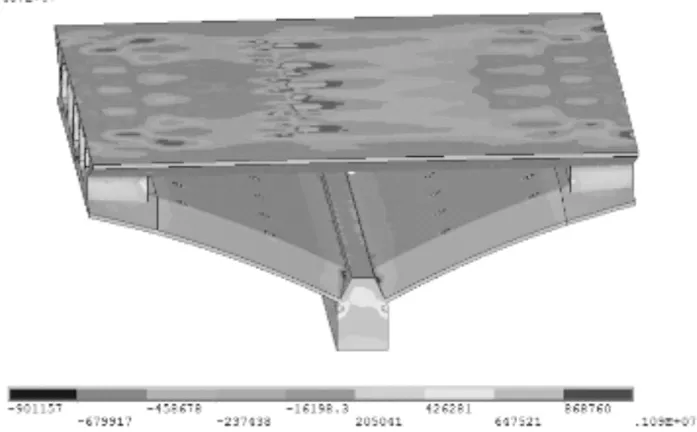
(a) 拱梁刚度比=0.5

(b) 拱梁刚度比=0.7

(c) 拱梁刚度比=0.9

(d) 拱梁刚度比=1.1

由图17可知，拱圈和拱座交界面处受力比较复杂，既有拉应力也有压应力。同时可以看出，随着梁拱之间刚度比值的变化，梁的相对刚度越大，系梁受力越大，但拱角空间应力较小；梁的相对刚度越小，拱圈受力越大，且在拱角附近产生应力集中现象。

4.2 运营阶段影响分析

选取9个关键截面进行分析：空腹区域系梁跨中截面、空腹区域系梁1/4跨截面、边梁与拱结合截面、左拱圈跨中截面、左拱圈1/4跨截面、右拱圈1/4跨截面、右拱圈跨中截面、中跨与拱结合截面、中跨跨中截面(见图18)，分析采用自重+预应力+二期+活载+整体降温+梯度正温差的工况。由于篇幅所限，图19仅给出边跨与拱结合3-3截面、空腹区域系梁跨中1-1截面、中跨与拱结合8-8截面以及中跨跨中9-9截面的受力状态(竖向挠度)随拱梁刚度比变化的结果。

图18 截面位置示意图Figure 18 Cross-section locations

由图19可知，各截面位置均随拱梁刚度比的增大而产生下挠减小的现象。具体来说，3-3截面位置梁体上挠，随着刚度比增大上挠增大；1-1截面处于空腹区域的系梁段，刚度比增大，系梁所受约束增强，故挠度减小；8-8截面是拱梁交结段截面，刚度比增大，截面刚度增大，故挠度减小；而9-9截面为中跨跨中截面，刚度比增大相当于中间梁段两端约束增强，故挠度减小。

经过类似分析，也可得到3-3截面顶板拉应力随拱梁刚度比增大而减小，1-1截面顶板压应力随拱梁刚度比增大而减小，8-8截面顶板拉应力随拱梁刚度比增大而增大，9-9截面顶板压应力随拱梁刚度比增大而减小。显然，应力的变化规律完全对应于挠度的变化规律。

综上可以看出，无论是施工阶段还是运营阶段，拱梁刚度比取值与相关构件挠度(刚度)以及应力(强度)大小息息相关，它可直接影响外力(施工与运营)作用下力学响应在不同结构体之间的分布，对拱梁刚度比进行合理设置，可实现梁拱组合体系桥梁的优化设计，确保该桥型在施工与运营阶段的受力安全和结构合理。

(a) 3-3截面

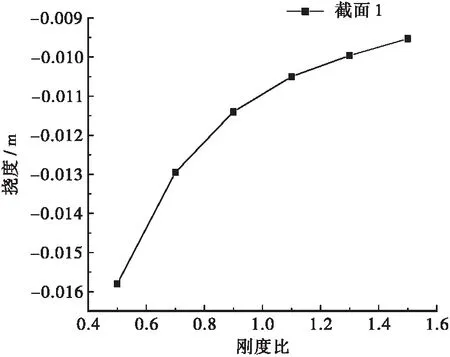
(b) 1-1截面

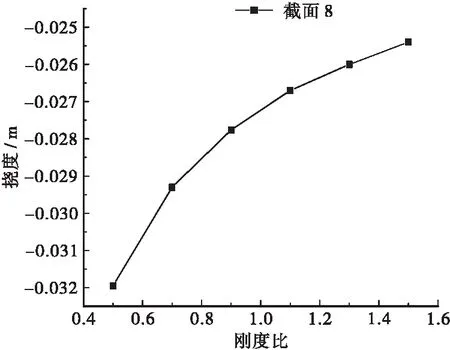
(c) 8-8截面

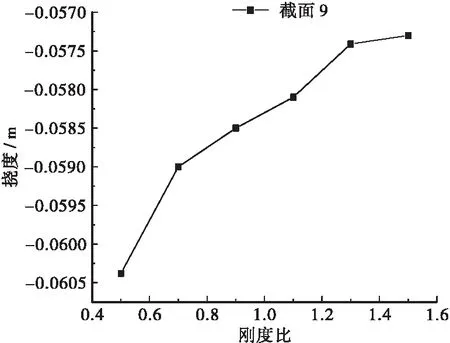
(d) 9-9截面

5 总结

a.利用ANSYS软件建立了有限元模型，基于单元生死理论对该桥施工阶段体系转化过程进行了精细化数值模拟。通过各个施工阶段控制截面纵向应力纵、横向分布来研究施工阶段应力分布规律。

b.通过不同桥宽关键截面的受力对比发现：宽跨比对边梁与拱结合截面顶板应力水平影响最大，其次是对中跨与拱结合截面顶板平均应力影响较大。

c.得到单箱6室、单箱5室这2种形式各控制截面顶、底板的应力分布情况，发现截面形式对边梁与拱结合截面顶板及中跨与拱结合截面顶板平均应力影响最大，其余各处应力水平变化较小。

d.通过4个不同刚度比的模型分析结果对比可知，刚度比增大，中跨跨中截面下挠减小，顶板压应力减小，底板拉应力增大。

e.无论是施工阶段还是运营阶段，拱梁刚度比取值与相关构件挠度(刚度)以及应力(强度)大小息息相关，它可直接影响外力(施工与运营)作用下力学响应在不同结构体之间的分布，对拱梁刚度比进行合理设置，可实现梁拱组合体系桥梁的优化设计，确保该桥型在施工与运营阶段的受力安全和结构合理。