基于多尺度卷积神经网络的交通标志识别方法

仲会娟，蔡清泳

(阳光学院 人工智能学院， 福建 福州 350015 )

0 引言

交通标志识别(traffic sign recognition,TSR)是智能驾驶的重要组成部分.但由于交通标志图像取自自然场景之中，容易受气候、光照、腐蚀、损坏、遮盖、运动模糊、旋转倾斜等因素的影响，因此如何提高图像的识别准确率受到学者们的关注[1].传统的交通标志识别算法有基于模板匹配、支持向量机(SVM)、随机森林等，但这些方法需要人为定义特征信息，如SIFT、HOG、SURF、LBP等特征[2-5].由于人为定义的特征容易忽略图像的很多内在有用特征，因此上述方法的识别精度有待进一步提高.近年来，随着深度学习的兴起，卷积神经网络因在图像检测与识别中能够获得较强的鲁棒性和较高的识别准确率而受到学者的关注.例如：文献[6]提出了一种二阶段多尺度特征分类算法，该算法在德国交通标志基准数据集GTSRB(German traffic sign recognition benchmark)[7]上的识别准确率为98.97%.文献[8]提出了一种基于支持向量机的交通标志图像分类算法，该算法在GTSRB数据集上的识别准确率为98.24%.文献[9]提出了一种三阶段多尺度特征分类算法，该算法在GTSRB数据集上的识别准确率为98.82%.

研究表明：图像的多尺度特征在人脸识别、数字识别、图像分割等领域具有良好的适用性[10-11]；VGG卷积神经网络模型因采用了多个小卷积层代替了单个较大卷积层，因此其网络深度得到增加，能够学习更为复杂的图像特征，且在感受野不变的情况下能够提高模型训练与图像识别的速度[12].基于上述研究结果，本文结合多尺度分类算法和VGG模型的小卷积核特性，提出了一种基于多尺度卷积神经网络的交通标志识别方法(traffic sign recognition method based on multi-scale convolutional neural network，TSR -MSCNN),并在自建的数据集和GTSRB数据集中验证了算法的有效性.

1 数据集介绍

1.1 自定义交通标志数据集

为减少网络训练时间以及能够验证算法的泛化能力，本文采用自定义数据集用于后期的参数对比实验.自定义数据集中有40类交通标志，共3 250张图片.图片分别取自比利时交通标志数据集及网络，格式为ppm，其中包含了光线遮挡、拍摄角度、拍摄模糊等复杂情况.由于ppm格式的图片无法直接看到，因此将图片转换为了jpg格式，如图1所示.同时，为了方便后期验证，对转换后的40类交通标志的图像集合进行了重新命名，如图2所示.

1.2 GTSRB交通标志数据集

GTSRB数据集中的标志图像由车载高清摄像头在自然环境下拍摄得到.数据集分为5大类和43小类，共51 839幅图片，其中12 630幅为测试集， 39 209幅为训练集，每张图片只包含一种交通标志，如图3所示.数据集中每类至少包含9种不同角度的图像，且每个角度包含从小到大的30张图片.

2 数据集预处理

因数据集中的交通标志图片是在多种自然条件下拍摄得到的，其图像质量和尺寸大小存在较大差别，因此需对图像进行预处理，以便更好地进行特征提取，提高模型精度.

2.1 尺寸归一化

GTSRB数据库中的交通标志图像的尺寸范围在15×15像素至250×250像素之间，因此需对其进行尺寸归一化处理.目前，常用于图像尺寸变换的算法主要有最近邻插值、双线性插值和双三次插值3种算法[13].其中，双线性插值法不但能够克服最近邻插值法不连续的问题，而且计算量小于双三次插值法；因此，本文采用双线性插值法对图像的尺寸进行归一化处理，归一化的尺寸统一设定为32×32像素.

2.2 像素归一化

图像像素的取值通常为0～255范围的整数.为了保持数据之间的相对关系和提高后续处理数据的速度，本文对像素进行了归一化处理，即将像素值压缩到0～1之间.

2.3 图像数据增广

TSR -MSCNN为三阶段卷积神经网络模型，具有识别准确率高、网络参数量低、识别速率快等优点，但该方法的模型训练需要大量的图像.为此，本文采用图像增广技术[14]来扩充训练数据规模.由于获取的交通标志图像常存在变形、角度和大小不一等问题，因此本文将原始图像以随机旋转10°、随机缩放0.2倍、随机平移(幅度为图像尺寸的0.08倍)和随机翻转的方式进行增广，增广的图像如图4所示.

3 基于多尺度卷积神经网络的交通标志识别法

3.1 二阶段多尺度卷积神经网络

传统的卷积神经网络是利用交替的卷积层和池化层获得图像特征信息，并将最后一层特征送入全连接层中进行分类识别.由于该方法识别图像的特征尺度单一，因此将该方法直接用于交通标志识别其效果并不理想.M.Zeiler等[15]研究表明，卷积神经网络能够提取出图像的多尺度特征信息，其中提取出的低阶特征反应的是图像中角、边缘等简单的局部特征，提取出的高阶特征反应的是图像的整体特征.二阶段多尺度卷积神经网络结构[6]如图5所示.

由图5可以看出，网络结构中包含2个阶段的卷积层， 2个池化层， 1个全连接层和1个分类输出层.其中，第1阶段卷积层的输出特征在池化后产生分支，该分支的输出特征经过第2个下采样点后与第2阶段卷积层的输出特征一同被送入分类器.

3.2 MS -TSRCNN模型

本文在文献[6]的基础上通过对网络结构和参数设置进行改进，提出了一种应用于交通标志识别领域的TSR -MSCNN模型，模型结构如图6所示.图6中：第1个子卷积网络Conv1由卷积层Conv11和Conv12构成，第2个子卷积网络Conv2由Conv21和Conv22构成，第3个子卷积网络Conv3由Conv31、Conv32和Conv33构成.Max_11和Max_22为2个尺寸统一的池化层，分别连接池化层Maxpool1及Maxpool2，其作用是将第1和第2阶段输出的特征图的尺寸统一为4×4像素.模型将尺寸统一的3个阶段的特征融合为交通标志的多尺度特征，并将多尺度特征送入全局平均池化层、全连接层进行交通标志分类.全局平均池化层的输入为：

GlobalAveragePooling merge_input=

[Max_11,Max_22,Maxpool3]

其中， []表示将Max_11、Max_22和Maxpool3的输出信号串联形成一个张量.

相比文献[6]的模型结构，本文提出的TSR -MSCNN模型做了如下改进：

1)改进了网络基本结构.①采用3阶段卷积神经网络结构代替2阶段卷积网络结构，以此增加网络深度，提高网络性能.②使用多个小卷积层串联代替单个较大卷积层，即在第1和第2阶段，用2个直接串联的5×5小卷积网络替换9×9的较大卷积层，在第3阶段用3个直接串联的5×5小卷积网络替换13×13的大卷积层，以此在保证算法感受野范围的同时，进一步增加网络深度以及减少网络的训练时间.③在每个子卷积网络中加入Batch Normalization (BN)算法，以此克服内部协变量偏移的问题，加快网络收敛速度.④使用全局平均池化(global average pooling)代替平坦层(flatten)，以此减少空间参数数量，使模型更加健壮，提高拟合效果.⑤在模型训练阶段，在保持输入输出神经元数量不变的情况下加入Dropout策略(每次随机关闭或忽略50%隐藏层神经元)，以此防止过拟合，提升网络泛化能力.

2)通过选比确定网络最佳参数.基本确定网络结构后，分别对全连接层神经元个数、Dropout参数、卷积核尺寸等网络参数进行选比实验，由此最终确定的全连接层神经元个数为256， Dropout参数为0.5， 卷积核尺寸为5×5像素.

4 实验结果与分析

实验使用的计算机为Windows 10操作系统，硬件环境为Inter(R) Core(TM) i5-7300HQ CPU@2.50 GHz，内存为8 G，显卡为4 G.本文的实验是基于Keras框架和TensorFlow开源库，并在Jupyter NoteBook开发环境中编程实现.

4.1 数据增广的有效性验证

在保持TSR -MSCNN网络结构与参数不变的情况下，对数据集增广前后的模型准确性进行对比.模型采用Adam优化器和Relu激活函数，初始学习率为0.001，每个实验中训练集迭代次数为50， 实验结果如表1所示.由表1中的数据可知，增广数据集后， TSR -MSCNN模型的识别准确率达到99.76%(原始数据集的识别准确率为99.32%)，由此说明增广数据集可大幅提高TSR -MSCNN模型的识别准确率.

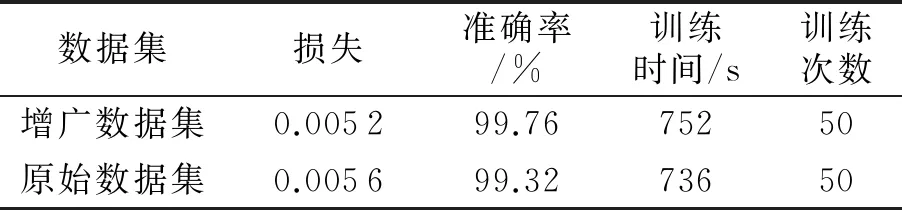
表1 数据增广前后的实验结果

4.2 多尺度特征的有效性验证

在保持网络参数不变的情况下，分别采用单尺度特征和多尺度特征对图像分类特征的种类进行对比，结果如表2所示.由表2中的数据可知，多尺度特征的损失和识别准确率优于单尺度特征，且二者的训练时间相同.由此表明采用多尺度特征对交通标志进行识别是有效可行的.

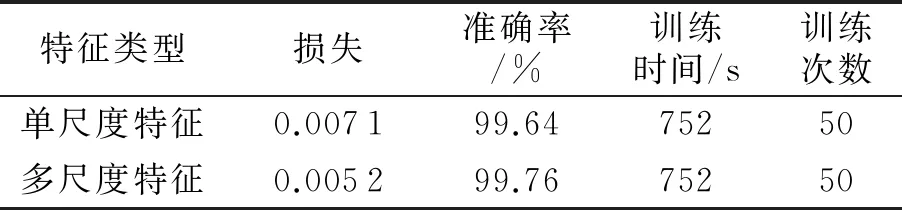
表2 不同分类特征的性能

4.3 小卷积核级联的有效性验证

1)在其他网络参数不变的情况下，对单个大卷积核模型与TSR -MSCNN模型进行对比，即用2个级联的5×5卷积核网络代替9×9卷积核，3个级联的5×5卷积核网络代替13×13卷积核，实验数据如表3所示.由表3中的数据可知，用小卷积核级联的TSR -MSCNN模型代替单个较大卷积核后，系统识别准确率得到有效提升，且系统总参数数量和网络训练时间大幅减小.由此表明，采用串联的小卷积核代替单个大卷积核对交通标志进行识别是有效可行的.

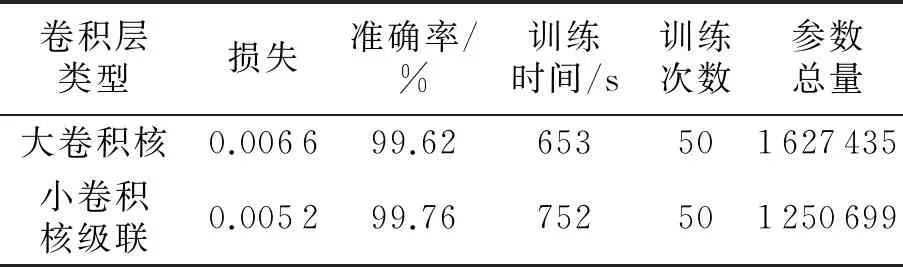
表3 不同卷积层的性能

2)在保持其他网络参数不变的情况下，通过改变网络中的卷积核尺寸进行尺寸选择实验.实验设置的卷积核尺寸分别为3×3、5×5、7×7，实验所得数据如表4所示.由表4可以看出：在3×3卷积核网络中，模型的训练时间最少，但网络的损失最大，且算法的准确率最低；在7×7卷积核网络中，模型训练花费的时间最多，但算法的准确率并不是最高；在采用5×5卷积核网络中，模型的训练时间虽然低于7×7卷积核网络和高于3×3卷积核网络，但网络的损失最小，识别准确率最高.因此本文在设计中选用5×5像素的卷积核.

表4 不同卷积核尺寸的性能

4.4 BN层的有效性验证

在保持相关网络参数不变的情况下，采用3种网络结构进行实验，结果如表5所示.由表5可知，每个阶段都加入BN层的网络结构，其训练时间虽然比未加入BN层的网络结构的训练时间有所增加，但其准确率最高.

图7为表5中3种网络结构训练的准确率和损失函数的变化曲线.由图7(c)可知，在3个卷积阶段分别加入BN层后，其识别准确率和损失函数的变化程度低于图7(a)和图7(b).由此表明, 在每个阶段分别加入BN算法对交通标志进行识别是有效可行的.

表5 有无加入BN层的网络性能

4.5 全局平均池化的有效性验证

在保持网络参数及其他网络结构不变的情况下，将模型中的Flatten层替换成全局平均池化层进行有效性对比，结果如表6所示.由表6中的数据可知，全局平均池化模型在损失、准确率、训练时间方面均优于Flatten模型，且二者的训练次数相同.由此表明，采用全局平均池化层来代替常规网络的平坦层对交通标志进行识别是有效可行的.

表6 全局平均池化模型和Flatten模型的性能

4.6 网络参数选比实验

为了验证和提高算法的泛化能力，减少系统训练所需消耗的时间，本文在自定义数据集中完成网络参数选比实验，实验包括Dropout最佳参数的选比实验和全连接层参数的选比实验.

1) Dropout最佳参数的选比实验.在TSR -MSCNN网络结构不变的前提下，改变Dropout参数设置进行选比实验，实验结果如表7所示.由表7中的数据可知：添加Dropout可以有效减少网络的训练时间.当将每层Dropout参数均设置为0， 即不添加Dropout层时，网络的识别准确率为98.46%，但模型的训练时间最长(351 s)；当将每层Dropout参数均设置为0.25时，网络的识别准确率最低；当将每层中Dropout参数均设置为0.5时，网络识别的准确率最高(98.85%)，损失最小，且模型的训练时间最短(101 s).因此，本文在设计中将各层的Dropout参数均设置为0.5.

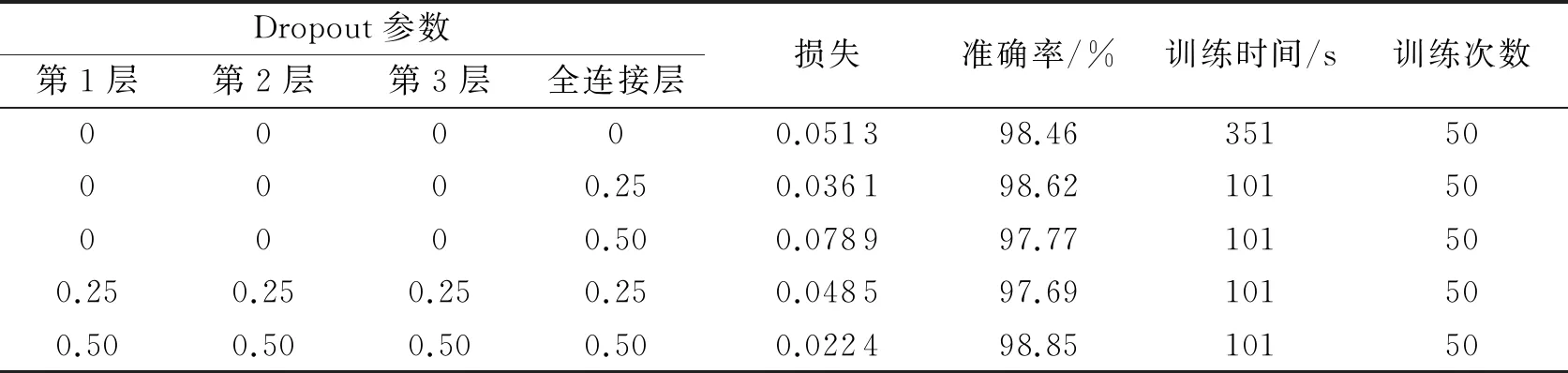
表7 Dropout最佳参数的选比实验结果

2)全连接层参数选比实验.在TSR -MSCNN网络结构不变的前提下，通过改变全连接层神经元的个数进行选比实验，实验结果如表8所示.由表8中的数据可知：全连接层神经元个数为1 024 时，所花费的训练时间最长；全连接层神经元个数为512时，损失最大，识别准确率最低；全连接层神经元个数为256时，算法的损失最小，识别准确率最高，且训练时间最短.因此，本文在设计中全连接层选用256个神经元.

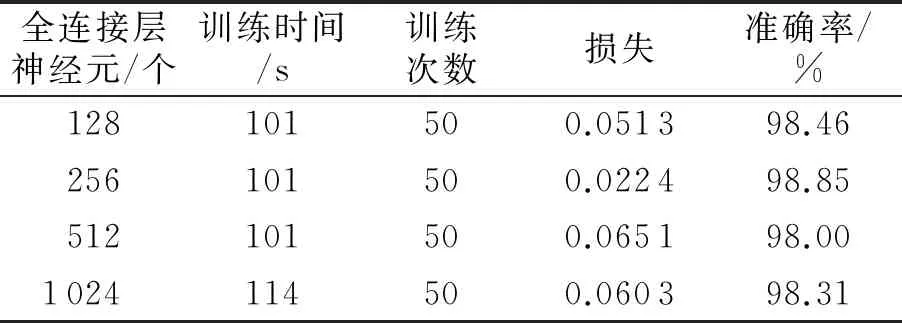
表8 全连接层最佳参数的选比实验结果

4.7 网络结构对比实验

在GTSRB数据集上测试了传统三阶段模型(模型1)、二次卷积特征连接模型(模型2)、TSR-MSCNN模型(模型3)、文献[6]的二阶段多尺度卷积神经网络模型(模型4)和文献[9]的三阶段多尺度特征分类算法(模型5) 5种网络结构的识别性能，结果见表9.其中：模型3采用2×2的最大池化层对不同阶段的卷积特征进行尺寸统一；模型2采用5×5的二次卷积层对各分支的输出进行尺寸统一；模型5采用单一的5×5卷积层提取3个阶段的卷积特征.

由表9可知，虽然模型3的训练参数数量略高于模型5和模型1，但模型3在5个模型中的识别准确率最高(99.76%)，损失最小，且训练时间最少；因此，综合来看，模型3的整体性能最优.

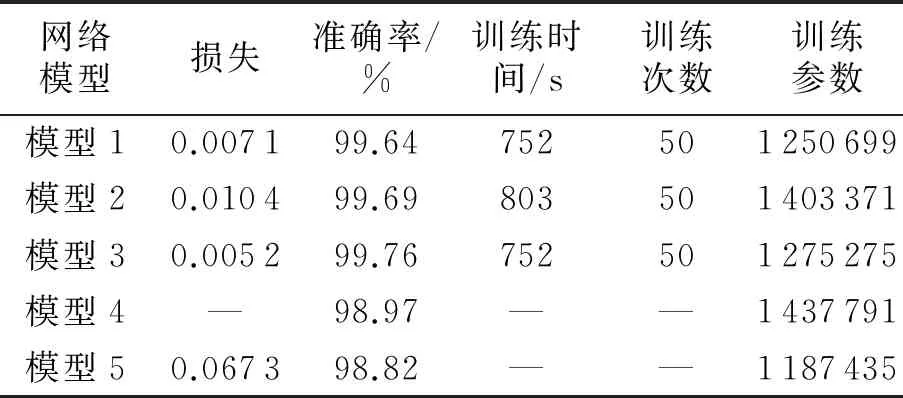
表9 不同网络模型的识别性能

5 结论

本文以轻量级卷积神经网络为基础，结合多尺度特征概念和串联的小卷积核，提出了一种应用于交通标志识别的多尺度卷积神经网络模型TSR-MSCNN.经实验表明，本文算法在自定义数据集和GTSRB数据集中的识别准确率分别为98.85%和99.76%，且整体性能优于文献[6]的方法，因此本文方法在交通标志识别领域具有良好的潜在应用价值.本文算法的识别速率还有待进一步改善.在今后的工作中，我们将尝试在卷积层中加入模型压缩算法来提高图像的识别速度，以进一步提高本文算法的适用性.