数控加工时间最优进给速度的光顺研究*
王 琦,王桂荣
(中国计量大学 机电工程学院,浙江 杭州 310018)
0 引 言
在航空航天、汽车领域的复杂零件的高精高速加工中,NURBS(non-uniform rational B-splines)插补应用广泛[1]。NURBS插补是在以NURBS曲线构成的待加工轨迹上,进行刀具进给速度规划,再计算每个插补周期的目标点坐标。其中,对NURBS曲线的进给速度规划对加工时间及质量有重要影响。
进给速度规划算法分为固定模式的加减速算法,如应用广泛且可实时进行的S型加减速算法[2,3],以及最优时间速度规划算法;其先建立数学最优模型,再采用线性规划[4]、粒子群算法(particle swarm optimization, PSO)[5]、启发式算法[6]等求解满足约束条件的速度曲线。最优算法往往需要较长时间迭代,一般用于离线速度规划,再进行实时插补。相比固定模式的加减速算法,最优算法搜索空间更大,可找到满足各种约束下的加工时间更少的速度曲线。速度曲线的高阶运动性质对加工有重要影响,罗亮等[7]指出加加速度越平滑,工作台振动幅值的增加量就越小。传统的加减速算法通过构造连续的加加速度曲线,如三次多项式的速度曲线[8],即可容易实现加加速度曲线的连续。然而,对于最优算法,一般通过限定加加速度上界来约束,速度曲线光顺性不足,加加速度曲线振荡幅度大,速度曲线上的一些小尖峰虽然加快了加工速度,以充分发挥机床的加减速性能,但是造成了加加速度的急剧变化,造成了振动。因此有必要对最优算法得到的进给速度曲线进行光顺。赵洋[9]将CAGD(computer aided geometric design)领域的能量光顺法应用到了速度曲线的光顺问题中,但未直接针对最优速度曲线,且光顺调整过程未考虑到可能引起的违反约束问题,光顺和曲线演化一起迭代进行,有很多重复的计算工作。
本文在采用启发式时间最优速度规划得到最优速度曲线的基础上,抓主要矛盾,提出固定部分区域光顺的方法,采用数学建模方法,基于能量光顺法对进给速度曲线的光顺性和时间性进行建模,利用最优化理论进行求解,为最优速度曲线的光顺性提供直接的改善方法,使加工时间和加工质量得到较好折衷。
1 进给速度时间最优化模型
1.1 待加工轨迹及进给速度曲线的数学描述
二维待加工轨迹可直接用NURBS曲线表示,对于直线圆弧或离散点构成的待加工轨迹可用NURBS曲线进行拟合,由于NURBS曲线具有可微性,可实现待加工轨迹的光顺。
NURBS曲线的定义[10]为:
(1)
式中:u—无量纲曲线参数;[x(u),y(u)]—u所对应的曲线上一点的坐标值;Pi—二维控制点i的坐标;wi—Pi对应的权因子;Ni,p(u)—节点向量U上的p次B样条基函数,其中,U=[u0,u1,…,un+p+1]。
u对应待加工轨迹的一点[x(u),y(u)],这一点的一维进给速度记为v(u),v(u)-u可表示为曲线的形式,v(u)用p次一维B样条来表示,即:
(2)
式中:Vi—等间隔u对应的一维控制点序列中序号为i的控制点,i=0~n。
可通过调整控制点的值来调整速度曲线。B样条曲线具有可微性,在节点区间内部是无限次可微的,有利于速度曲线的光顺性;同时,B样条曲线又具有局部性,即调整一个控制点,仅对其周围的曲线有影响,有利于局部调整曲线与约束检查。
此处的B样条次数取3次。
1.2 约 束
进给速度规划一般受以下3类约束限制:
(1)弦高误差约束:
(3)
式中:ρ—曲率半径;Ts—插补周期;emax—加工允许的最大弦高误差;v—当前进给速度。
(2)工艺限制约束:
(4)
式中:vu—v(u)对参数u的导数;Pu—待加工轨迹P(u)对u的一阶弧微分;au—a(u)对参数u的导数;Vmax,Amax,Jmax—工艺要求的刀具速度、加速度、加加速度极限。
(3)机床驱动限制约束:
(5)

1.3 最优模型
对于给定的NURBS待加工轨迹P(u),进给速度规划的目标是在满足上述式(3~5)约束的前提下,尽可能提高速度,以减小加工时间。
决策变量是速度曲线v(u)的控制点值,目标函数为加工时间的最小化,即:
(6)
2 光顺算法
为降低机床加工时的振动,提高工件的加工质量,时间最优的进给速度需要光顺。光顺性的定义较为模糊,一般认为光顺曲线不存在奇点和多余拐点、曲率连续,且变化较小、应变能较小。进给速度的光顺指提高对应加工轨迹的进给速度曲线的光顺性。
本文面向时间最优的速度曲线进行光顺,首先由启发式速度规划获得时间最优的速度曲线,然后对于已接近加工时间最优的速度曲线:
(1)由于能量光顺法是没有方向性的,任一点的速度都可能变大或变小,容易超过约束限制;
(2)另外,加工时间的最优性不能因为改善光顺性而大量下降。
基于以上两方面,笔者提出固定部分区域的光顺算法。
2.1 获得加工时间最优的进给速度曲线
可由启发式算法来获得时间最优的进给速度曲线,算法步骤为:
(1)生成初始的B样条速度曲线,需确定控制点数量n、曲线次数p、节点向量U,控制点初始值为单个插补周期能从零达到的满足约束的最大速度;
(2)对控制点进行一轮调整,依次调整第2~n-1个控制点值,单个控制点采用二分法迭代[11]调整;
(3)计算本轮调整后的平均速度与上一轮的差值,若小于阈值,则获得时间最优的速度曲线,控制点向量记为V0,结束;否则,返回(2)。
2.2 固定部分区域的速度曲线光顺算法
2.2.1 算法思路
部分区域首先指速度极小值区域,其次指固定极小值区域进行光顺后出现的超限区域。低速区域的速度大小对加工时间的影响非常重要,将低速区域固定,保持低速区域的最优性,在此基础上通过设置较大的逼近因子,使其余区域的最优性大致保留。
此外,部分区域固定,其余区域的速度曲线整体会向固定区域靠近,这使得固定速度极小值区域后,速度的调整大致为向下调整,从而使超限的情况大量减少。对于光顺后出现的超限区域,也将其作为固定区域,这样光顺前后这块速度曲线与原来相同,则满足约束。
2.2.2 固定部分区域光顺的优化模型
能量法是曲线光顺常用的一种方法,本文算法在此基础上进行,通过曲线的应变能来反映光顺性,曲线应变能越小光顺性越好,光顺后曲线应变能为:
(7)
式中:α—曲线的光顺因子;k—曲线曲率。
曲率k可近似为B样条速度曲线对参数的二阶导,即:
(8)
式中:v(u)—光顺后u处的进给速度值。
将式(8)代入式(7),经计算可得:
(9)
此外,光顺后的速度曲线要与原来的时间最优速度曲线相差尽可能小,曲线光顺前后的偏离量记为:
(10)

决策变量是控制点序列的值。目标函数为E1、E2都需要最小化,将双目标加权合为单目标。固定部分区域通过对相应控制点保持光顺前后不变来实现,在优化模型中作为约束条件出现。
现将固定部分区域的速度曲线光顺的优化模型表示如下:
决策变量:
V=[V0…Vj…Vm+2]T
(11)
(1)目标函数:
(12)
(2)约束函数:
(13)
式中:l—固定区域的控制点序号。
(3)优化模型的求解
以上是有等式约束的凸优化问题,一般用拉格朗日乘子法解决,但该问题中,约束函数中能确定一些变量即固定控制点的最终值,那么问题可以看作比原来少一些变量的无约束凸优化问题,可直接对变量求偏导得到最优值。

方程的通用形式为:
(14)
对式(14)进行化简,且将α拓展为αi可得:
(15)
若控制点Vi需要固定,可将αi置为0,则有:
(16)
将式(14)中的Vj(j=0~m+2)提出到列向量中,m+3个等式写成矩阵形式,即:
AV=C
(17)
式中:V—待求的控制点列向量,V=(Vi)m+3,1;A,C—m+3个等式中V提出后得到的矩阵、向量,A=(aij)m+3,m+3,C=(Ci)m+3,1。
其中:
(18)
式(18)的积分可采用梯形法计算,V的求解可采用高斯消元法。这样通用形式求解的V与固定的控制点作为常量,其余控制点作为变量的无约束凸优化问题同解,也与式(11~13)的等式约束的凸优化问题同解。
2.2.3 算法步骤
(1)扫描控制点值确定多个极小值和极大值,将极小值对应的控制点索引加入G,极大值的加入M;G代表固定的控制点的索引集合;
(2)对每个极小值左右相邻的一个控制点,若该控制点的索引不属于G或M,则加入G;此时G所代表的控制点成为极小值区域;
(3)将G对应的控制点的光顺因子αi置为0,实现光顺算法中最小值区域的固定;
(4)进行固定区域的能量光顺,即对式(17)构成的矩阵方程求解V;
(5)将求出的V构成B样条曲线,检查超限区域,将超限区域附近的控制点值置为时间最优规划的结果值,将这些控制点依次加入G,转入(4),直到满足约束或超限区域全部控制点加入G。
3 实验及结果分析
为验证本文方法的正确性和有效性,笔者在MATLAB上进行仿真分析,在加工时间上和速度曲线的光顺性方面,将所提算法与启发式时间最优算法进行比较;在加工时间上,与三角函数型加减速算法[12]进行比较。
所提算法与启发式算法需要设置的参数如下:
B样条曲线参数:曲线次数p=3,控制点数量n=201,节点向量采用准均匀的B样条曲线进行生成;
启发式算法:二分最大次数Ns=10,收缩因子Rf=0.68,结束迭代阈值为1,检测步长0.000 1。
能量光顺中,光顺因子初始化为2×10-8,逼近因子初始化为9.8×10-7。得到进给速度后,插补方法使用二阶泰勒展开法[13],得到插补步数后,计算加工时间。
笔者在相同的数控加工参数下和相同的待加工轨迹上运行不同的算法。
数控加工参数如表1所示。

表1 数控加工参数
待加工蝴蝶形NURBS轨迹如图1所示。

图1 待加工蝴蝶形NURBS轨迹
3.1 规划结果及约束情况分析
按以上参数,本文所提算法与时间最优法规划的进给速度对比如图2所示。

图2 所提算法与时间最优法规划的进给速度对比图
图2中,本文算法规划的进给速度符合小于250 mm·s-1的约束,两条曲线基本重合,说明保留了时间最优性,但振荡处进行了光顺(详见图2中的放大处)。
所提算法与时间最优法进给加速度对比如图3所示。
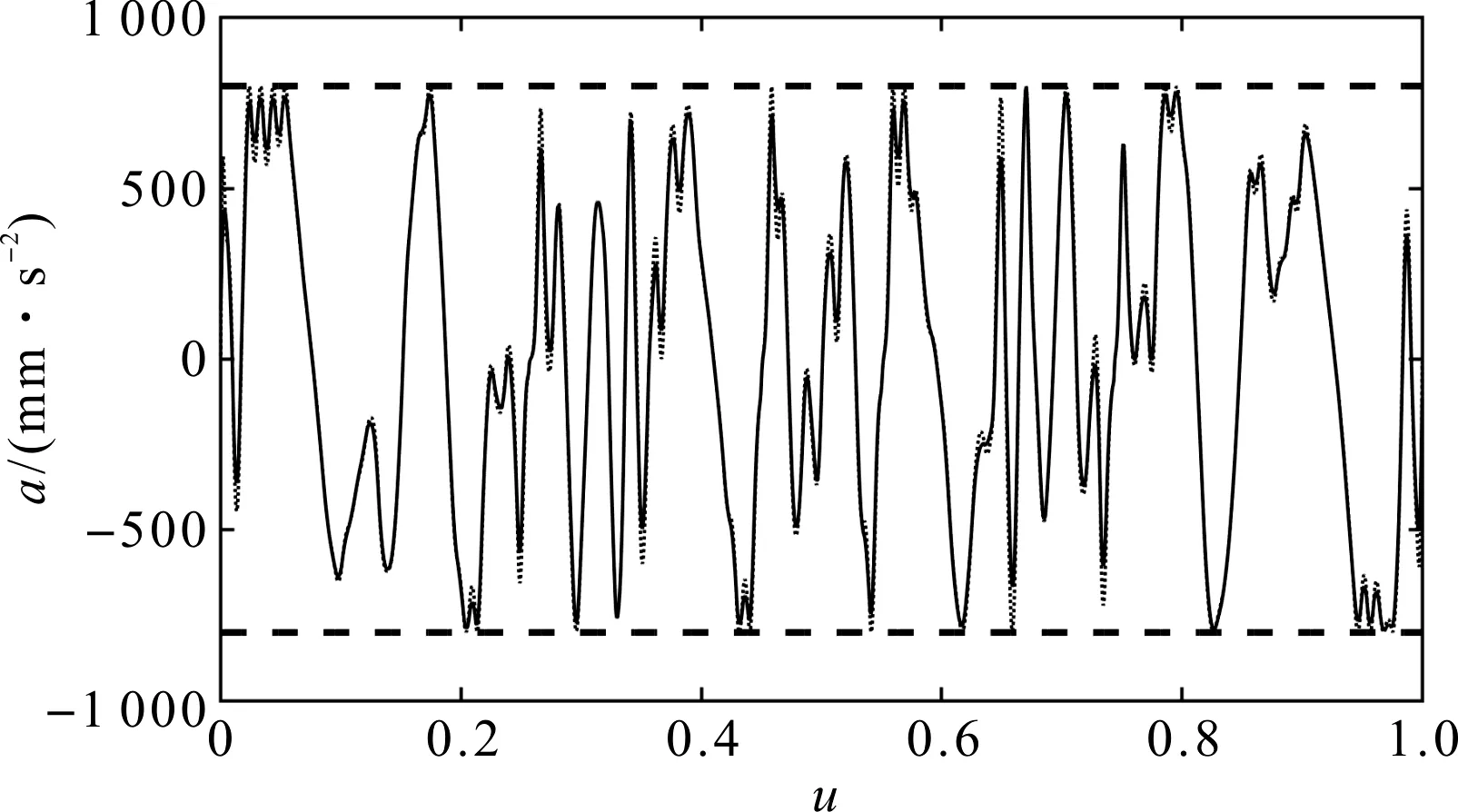
图3 所提算法与时间最优法规划的进给加速度对比图
由图3可知:本文所提算法的进给加速度符合小于800 mm·s-2的约束;且相比于时间最优法,一些尖峰值减小,振荡区域幅度也减小。
本文所提算法与时间最优法进给加加速度对比如图4所示。

图4 所提算法与时间最优法进给加加速度对比图
由图4可知:本文所提算法的进给加加速度符合小于26 400 mm·s-3的约束;且相比于时间最优法,多处尖峰值明显减小,振荡区域幅度也减小。
本文所提算法与时间最优法单轴加加速度对比如图5所示。

图5 所提算法与时间最优规划法单轴加加速度对比图
由图5可知:本文所提算法的单轴加加速度符合小于26 400 mm·s-3的约束,相比于时间最优法,多处尖峰值明显减小,振荡区域幅度也减小;此外,弦高误差、单轴速度、单轴加速度都符合表1约束。
结合图(2~5)可知:本文所提算法通过平缓速度振荡较大的区域而其他区域基本不变,使得相应的加速度、加加速度及单轴的加速度和加加速度振荡幅度减小,从而降低了机床加工时的振动,且保留时间最优性。
3.2 光顺性与时间性分析
笔者使用加速度、加加速度的平均采样步长改变量来表示振荡程度,采样步长0.000 1。
两种算法单轴运动性质光顺性对比如表2所示。

表2 两种算法单轴运动性质光顺性对比
由表2可知:与启发式时间最优法相比,本文所提算法的x、y轴加速度曲线的平均采样步长改变量平均下降8.34%,x、y轴加加速度曲线的平均采样步长改变量平均下降16.37%;由此可见,单轴运动性能的光顺性得到了较大改善。
在蝴蝶形NURBS待加工轨迹上,不同算法加工时间如表3所示。

表3 不同算法加工时间对比表
由表3可知:本文算法比启发式时间最优规划算法仅多用了0.22%的加工时间,比三角函数型加减速算法少了19.8%的加工时间;可见,经本文的算法光顺后,保留了大部分的时间最优性。
4 结束语
本文对数控加工速度规划的加工时间和加工质量的平衡问题,进行了时间最优速度曲线的光顺研究,提出了固定部分区域的光顺算法,经仿真实验结果表明,在满足速度规划约束和保留大部分时间最优性的前提下,可以实现进给速度曲线的光顺;同时,可以减小加速度、加加速度及单轴相应性质的振荡程度,有利于实现高速高精加工。
该算法中,目前对速度极小值区域的范围界定方法简单,因此,如何更精细地确定范围以获得更好的时间性和光顺性,这是下一步需要进行的研究。同时,该方法还有待与其他的时间最优性算法相结合;所面向的二维NURBS加工曲线还有待于向三维曲面加工方向进行拓展。

