基于EMDD信息量和KNP-SVDD的滚动轴承故障诊断研究*

陈宇晨，何毅斌，戴乔森，刘 湘，贺苏逊

(武汉工程大学 机电工程学院，湖北 武汉 430205)

0 引 言

滚动轴承被广泛应用于各种机械中。能够及时地对滚动轴承进行监控，检测其是否受损，对工业生产具有重要的意义[1]。滚动轴承的故障检测主要包括信号采集、特征提取、故障分类3个步骤。由于信号采集的过程中存在一些噪声，导致特征提取不准确，需要对采集的原始信号进行处理。确保得到有用的特征是对故障进行准确分类的重要保障[2]。

在对滚动轴承的信号进行处理和特征提取中，常用的方法有傅立叶变换(FT)、小波变换(WT)以及经验模态分解(EMD)等。FT和WT需要事先设定基函数，对非平稳信号的处理效果不好；EMD则是根据自身的时间尺度进行分解，可以很好地用于非平稳的信号，但EMD具有端点效应和模态混叠等缺陷。为了解决EMD的不足，集成经验模态分解(EEMD)被提出，并广泛应用到故障诊断的信号处理和特征提取过程中[3]；故障分类常用的方法有人工神经网络(ANN)、支持向量机(SVM)等，ANN需要很大的数据量以及很长的训练时间，而SVM可用于小样本训练，训练速度快，对于线性和非线性数据都有很好的分类效果，因此SVM广泛被应用于故障诊断的故障分类过程中[4-6]。

为提高SVM分类的准确率，得到最佳的分类效果，需要使用一些优化算法，为SVM计算更好的惩罚参数以及核参数。陈法法等[7]提出了EEMD能量熵和优化LS-SVM结合的滚动轴承故障检测方法；何青等[8]提出了EEMD能量熵和MFFOA-SVM结合的滚动轴承故障检测方法；姬盛飞等[9]提出了AFSA-SVM的滚动轴承故障检测方法；梁治华等[10]提出了EEMD能量熵和CS-SVM结合的滚动轴承故障检测方法。

上述方法均取得了不错的效果，但由于SVM的限制，这些方法并不适用于各类别的样本数量不均衡的情况[11-13]，这种不均衡导致分类结果偏向于样本数量较多的那一类。

为了解决以上问题，研究人员引入了K相邻概率支持向量数据描述(KNP-SVDD)方法。SVDD是TAX D等[14，15]在结构风险最小化的SVM基础上提出的单类描述方法，但这种方法仅可以用来判断样本是否属于某类。为了将SVDD扩展到多分类，王涛等[16]通过训练多个SVDD模型，并比较样本到每个SVDD模型的相对距离的大小来判断样本的种类，该方法仅考虑模型对样本的影响而未考虑样本附近点对其影响，对越靠近SVDD模型边缘的样本判决结果的可靠性越低。付文龙等[17]利用K最近邻(KNN)和SVDD法组合为I-SVDD方法判断样本的类别，即对同时满足多个SVDD模型的样本使用KNN方法根据其附近样本的信息判断类别，该方法仅考虑样本附近点对其的影响而未考虑模型的影响,在训练样本少或各类别不均衡的情况下分类效果不好。

在此基础上，笔者引入KNP-SVDD方法，这种方法综合考虑模型以及样本附近点对其的影响，既包含整体的信息又包含局部信息，最后通过第三方实验数据，对该方法的诊断效果进行验证。

1 集成经验模态分解与信息量特征提取

1.1 集成经验模式分解

集成经验模态分解(EEMD)建立在经验模态分解(EMD)的基础上，通过往原信号中加入满足分布的白噪声信号，利用这些噪声均值为0的特性，均衡原信号噪声的特性，有效抑制了EMD中的模态混叠等缺陷。

EEMD的主要过程如下：

(1)在原始信号xold中加入满足N(0,σ2)分布的白噪声信号ε，组成新的信号xnew，即：

xnew(t)=xold(t)+ε～N(0,σ2)

(1)

(2)利用EMD方法，将信号xnew(t)分解为组本征函数(IMF)与一组残余分量(RES)之和，即：

(2)

上式中，随着的数值由1向n增大，对应的IMFi的频率宽度越小；

(3)重复(1～2)m次，共得到m组不同的{IMF1…IMFn,RES}，对m组求平均值：

(3)

可见，经过平均得到的结果即为EEMD分解后的各频率段的信号。

1.2 信息量特征提取

对滚动轴承故障的检测主要是通过在不同位置设置传感器，测得其振动信号。笔者根据振动信号对轴承故障进行判断，通过EEMD将测得信号分解为不同频率段的IMF以及残余分量RES；特征提取就是从不同频率段的IMF提取出具有代表性的量[18]。

本文选择不同频率段IMF的信息量作为特征，特征提取的主要步骤如下：

(1)假设第i个IMF在j时刻的函数值为fi(j)，则第i个IMF的幅值能量Ei可以表示为：

(4)

(2)该信号的总能量Esum可以表示为：

Esum=∑iEi

(5)

(3)对各频率段IMF的幅值能量归一化处理，即：

pi=Ei/Esum

(6)

(4)计算各频率段IMF的幅值能量归一化处理后的信息量：

Hi=-log2(pi)

(7)

最后，将信息量{H1,H2,…Hn}作为特征，输入到分类算法中。

2 K相邻概率支持向量数据描述

2.1 支持向量数据描述

支持向量数据描述(SVDD)是一种单类数据描述算法[19]，它将目标类数据通过核方法映射到一个高维空间，并在高维空间中，通过目标类训练样本描述出一个最符合样本的超球体；由于是对某一种样本的描述，其不会受到不平衡样本的影响。

设X1={x1,x2,…xn}为收集到的n组同类别的样本，该类别外所有的样本集合可表示为X2={xn+1,xn+2…xn}。

此时，问题可表述为利用样本X1求目标超球体的原点a和半径，该目标被表示成一个二次约束二次规划(QCQP)的问题，即：

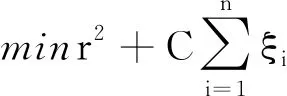
(8)

式中：C—误差惩罚项系数：ξi—松弛变量，允许部分训练样本的不在超球体内的情况出现；φ(·)—一个将向高维空间映射的函数，用于解决样本在当前空间超球体描述会造成很大误差的情况。

为了求解QCQP问题，笔者构建拉格朗日函数如下：

(9)

式中：λ，υ—拉格朗日乘子，且λ，υ≥0。

对式(9)中半径、圆心a和松弛变量ξi求偏导,并令结果为0，则有：

(10)

将式(10)代入式(9)中，则式(8)的对偶形式可以表示为：

(11)

上式中φ(·)，的形式未知，但φ(x)间的内积可以通过核函数K(·)计算，核函数需满足的条件如下：

K(xi,xj)=(φ(xi),φ(xj))

(12)

本文使用的核函数均为高斯核函数，即：

(13)

式中：σ—核宽度参数。

通过求解上述约束优化问题，可计算出符合样本的超球体中心坐标。

对于训练样本中的所有点，到圆心的距离需满足以下3种条件：

(14)

(15)

对于新的样本z是否与训练样本属于同一类，可以利用其到球心的距离与半径的大小进行判断，即：

(16)

若上式的结果小于等于0，表示样本z与训练样本为同类。

2.2 K相邻概率支持向量数据描述

为了将SVDD扩展到多元分类，通常采用组合SVDD的方法。组合SVDD圆形描述图如图1所示。

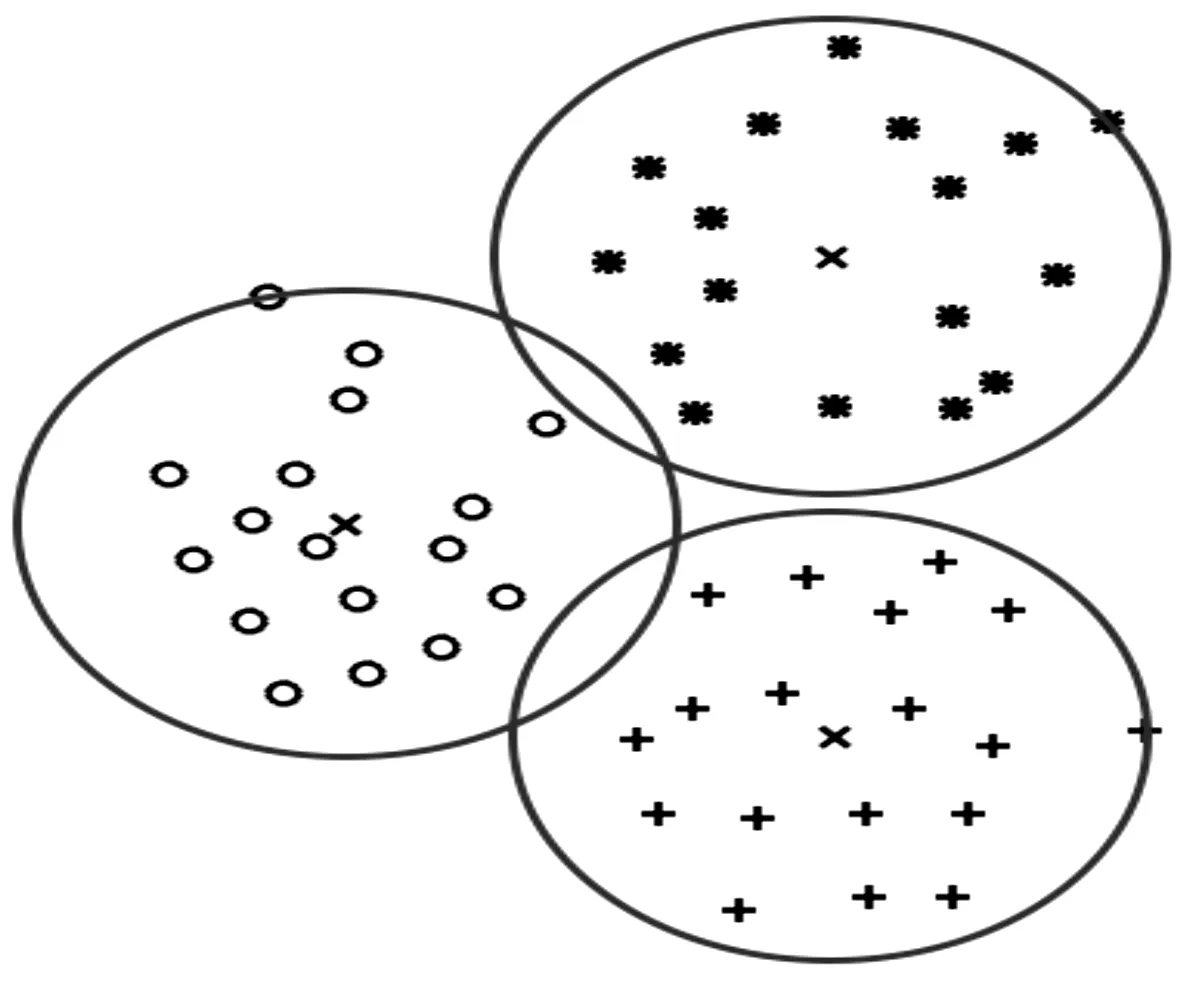
图1 组合SVDD圆形描述图

图1中，使用SVDD方法对每一类别的数据做1次训练，组合多个圆形描述使之成为1个多类别分类器，再通过测试样本到球心的距离与半径的大小判断其类别[20]。但SVDD只是针对未知结果的二值输出，若某一个测试样本落在多个圆形的相交区域，测试样本将同时被判定为多个类别。

为了处理以上这种情况，笔者利用1种基于概率的支持向量数据描述(P-SVDD)方法，将测试样本的球心的距离转换为属于该类别的概率[21]，即：

(17)

式中：pi—测试样本属于第i个超球体概率；di—测试样本到第i个超球体中心距离；ri—第i个超球体半径。

当di逐渐增大时，pi逐渐减小；当di=0时，pi趋近1；当di=ri时，pi=0.5；当di趋近于无穷时，pi趋近0。通过计算测试样本属于每个超球体的概率，即可判定测试样本为概率最大的一类。

对于第i类SVDD中的惩罚项系数C和核宽度参数δ，可利用1组标签为Y={y1,y2…yn}的样本，并通过公式进行优化，即：

(18)

式(18)中，当计算的概率与真实的情况相差越远时，会赋予越大的惩罚；通过最小化惩罚，可以得到最佳的参数C、δ，从而得到最佳的SVDD模型。

将概率作为分类的判据，仅考虑了测试样本与超球体的半径和中心的信息，而没有考虑到测试样本附近点的信息，即只考虑到了总体的信息，未考虑到局部的信息。

信息的不足会导致对超球体边缘附近部分点的判决结果可信度不高，所以需要综合考虑这些因素的影响，更新测试样本的概率，具体的步骤如下：

(1)设有训练样本X={x1,x2…xn}及标签Y={y1,y2,…yn}和测试样本z，将z代到所有的训练并优化好的SVDD模型，得到的概率为p1…pn；

(2)若p1…pn中没有值大于0.5，则判决测试样本不属于任何一类；若p1…pn中仅有一个值大于0.5，则判决测试样本z属于p1最大的那一类；若p1…pn中有两个以上的值大于0.5，利用下面的步骤更新大于0.5的概率pi；

(3)计算样本到训练样本X中所有样本的平方距离，即：

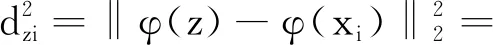
(19)

(5)选择样本z的k个附近的样本，将p更新为：

(20)

式中：f(·)—同式(18)；ω—权重参数。

更新后的概率可以看作是原概率与其附近样本分布的加权。这种方法的可取之处是，既考虑了总体的信息，又考虑了局部的信息。

3 实验及结果分析

笔者采集了正常、内圈故障、外圈故障、滚动体故障4种状态的轴承振动信号；轴承的转速为1 000 r/min，采样频率为50 kHz，采集的时间为5 s，根据条件可计算出当轴承每转动一圈时，采样的信号数量为60×50 000/1 000=3 000个，采集5 s时共采样250 000个信号；以3 000个信号为一组，每种类别的故障信号共采集80组。

为了构造不平衡数据，笔者对滚动故障类仅选择40组，从每种类别中随机选择60%作为训练样本，40%作为测试样本。

故障类型代号及抽样数量如表1所示。

表1 故障类型代号及抽样数量

表1中，对3类故障样本数量选取较少，构造了一组不平衡的数据。笔者从每种类别中随机选择60%作为训练样本，40%作为测试样本，对所有数据利用EEMD分解分别提取其特征。

笔者选择EEMD分解得到的前7阶IMF的信息量作为样本的特征，粒子群优化(PSO)计算惩罚项系数以及核宽度参数，取附近样本数为10，权重参数为0.5。

KNP-SVDD单次诊断分类图如图2所示。

图2 KNP-SVDD单次诊断分类

图2中，利用KNP-SVDD方法，将表1测试样本中，16个第3类故障中的15个进行了正确分类。

该方法对112个测试样本进行了测试，其中107个取得了正确的分类，准确率达到了98.214 3%。

为了比较不同方法之间的差异，笔者分别利用I-SVDD和相对距离SVDD(RD-SVDD)、PSO-SVM方法训练分类器，SVM方法，用一对一方法扩展到多分类器。

I-SVDD单次诊断分类图如图3所示。

图3 I-SVDD单次诊断分类

图3中，利用I-SVDD方法，将表1测试样本中，16个第3类故障中的15个进行了正确分类。

该方法对112个测试样本进行了测试，其中107个取得了正确的分类，准确率达到了95.535 7%。

RD-SVDD单次诊断分类图如图4所示。

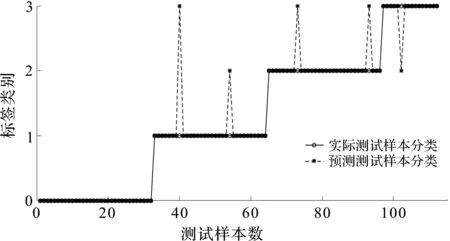
图4 RD-SVDD单次诊断分类图

图4中，利用RD-SVDD方法，将表1测试样本中，16个第3类故障中的15个进行了正确分类。

该方法对112个测试样本进行了测试，其中107个取得了正确的分类，准确率达到了95.535 7%。

PSO-SVM单次诊断分类图如图5所示。

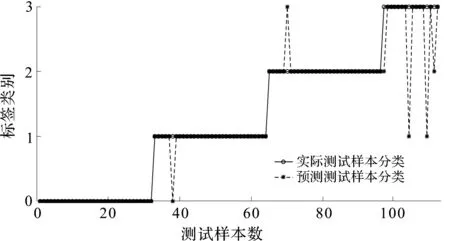
图5 PSO-SVM单次诊断分类图

图5中，利用PSO-SVM方法，将表1测试样本中，16个第3类故障中的11个进行了正确分类。

该方法对112个测试样本进行了测试，其中106个取得了正确的分类，准确率达到了94.642 9%。

将3类的16个测试样本分对11个，并在所有测试样本上达到了94.642 9%的准确率。

图(3～5)中，由于3类故障类型的训练样本数据量较小，导致PSO-SVM方法对这类样本的误分率较高，而I-SVDD方法也会因这种不平衡，导致在该样本上的分类效果不好。利用RD-SVDD方法可以有效对这种不平衡类别的样本分类，上面3种方法的总体准确率大致相同。而无论是在不均衡数据的分类效果，还是总体分类准确率方面，KNP-SVDD方法在这几种方法中均表现最好。

上面的结果仅代表1次诊断分类的结果，为了计算更准确的分类准确率以及对少数样本的误判个数，笔者重复上文的训练测试过程20次。

平均测试结果如表2所示。

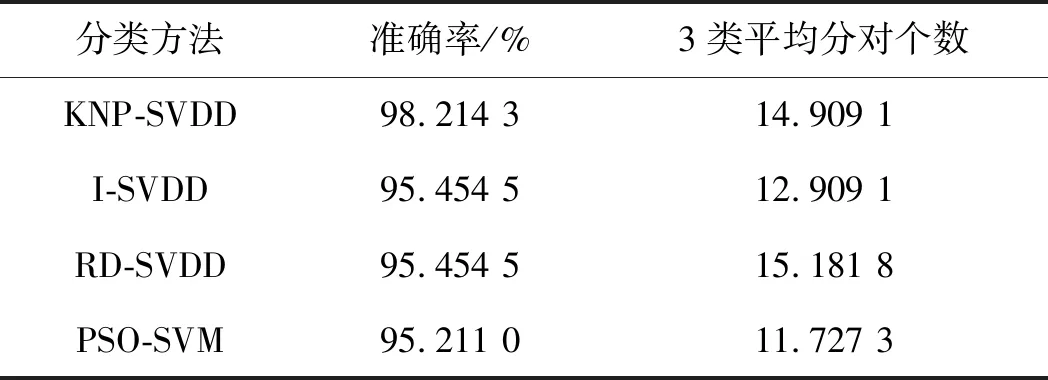
表2 平均测试结果

表2中，在多次重复实验下，ISVDD、RD-SVD与PSO-SVM这3种方法总体分类准确率差别不大，但RD-SVDD对数据量较少类别分类效果较好，证明了SVDD方法处理各类样本不均衡数据的有效性；而PSO-SVM、I-SVDD方法对数据量较少的类别分类效果较差，说明在样本量小且不均衡的条件下，SVM方法并不合适；而KNN方法仅考虑局部信息会导致SVDD方法失去部分算法本身的优势，KNP-SVDD方法对比其他方法得到了最高的总体分类准确率，对数据量较少类别分类效果也较好，证明了该方法的可行性和有效性。

笔者利用美国凯斯西储大学轴承实验室标准数据库的轴承数据，再次对本文的方法进行验证。其中，选择电机负载为0 hp，轴承的转速为1 797 r/min，采样频率12 kHz的驱动端数据测试，故障类型分为10类。

故障类型代号及抽样数量如表3所示。

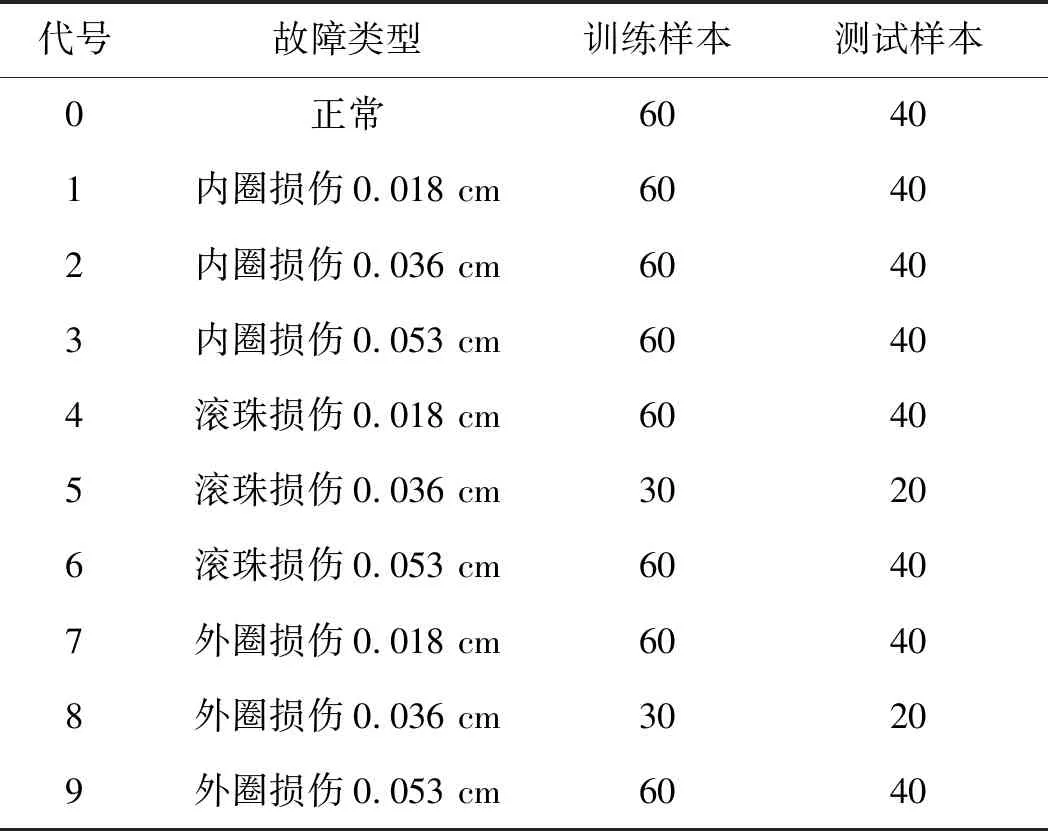
表3 故障类型代号及抽样数量

表3中，每种类型60%作为训练样本，40%作为测试样本，选择EEMD分解得到的前6阶IMF的信息量作为样本的特征，取附近样本数为15，权重参数为0.5。

不同方法分类准确率如表4所示。

表4 不同方法分类准确率

不同方法对每种故障分类准确率如图6所示。

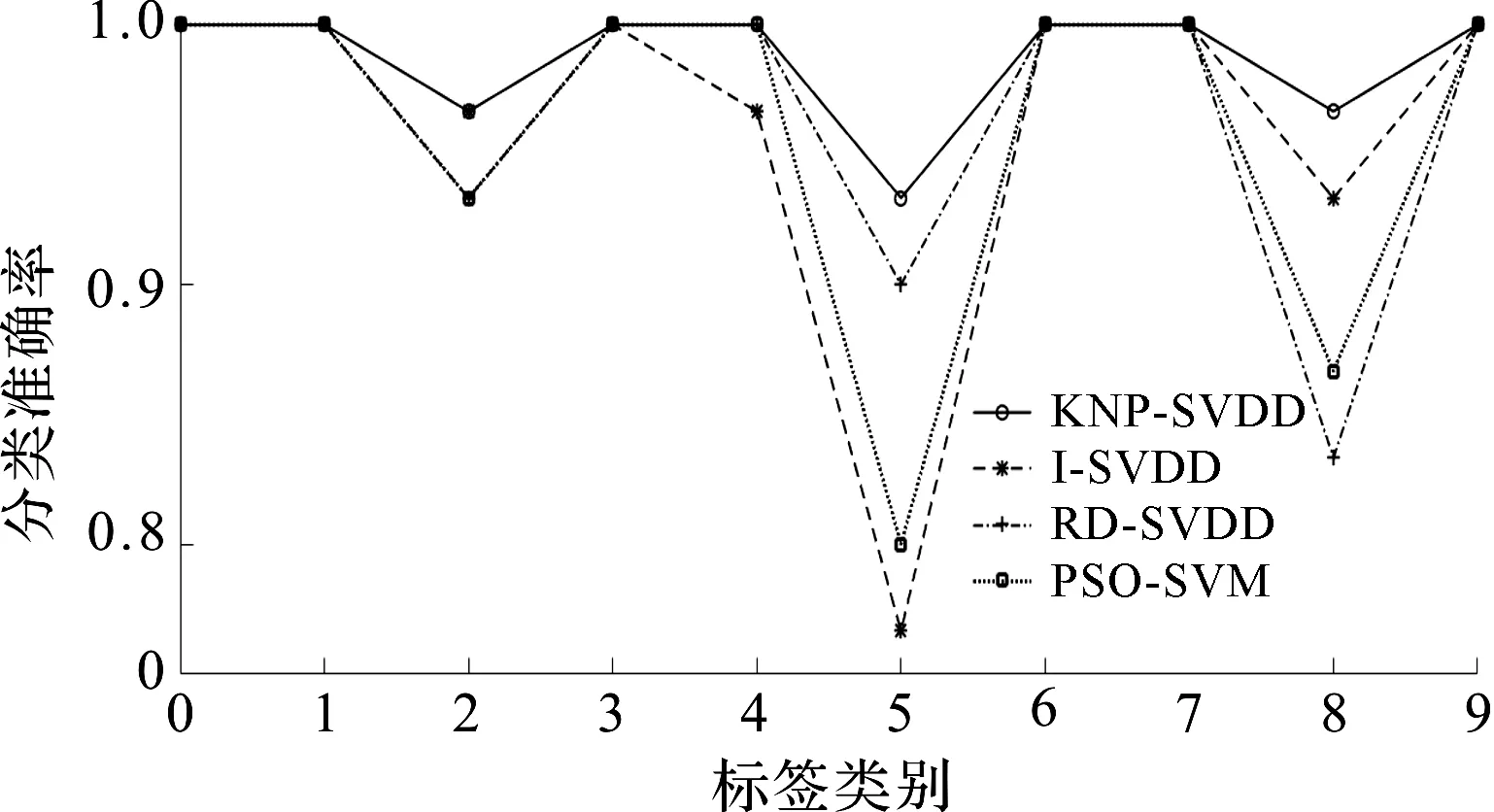
图6 不同方法对每种故障分类准确率

表4和图6中，通过对比这4种方法可知：

(1)PSO-SVM方法对第5类和第8类故障类型的分类效果较差，I-SVDD方法对第8类故障类型的分类效果较好，但对第5类故障类型的分类效果较差；

(2)RD-SVDD方法对第5类故障类型分类效果较好，对第8类故障类型的分类效果较差；

(3)KNP-SVDD方法在全部测试样本上，以及每一种故障类别上的分类准确率均达到了最高，再一次验证了该方法的可行性和有效性。

4 结束语

本文基于K近邻(KNN)法和概率支持向量描述(P-SVDD)法，提出了K相邻概率支持向量数据描述(KNP-SVDD)法，用于提升各类数据分布不均匀的情况下的滚动轴承故障诊断的识别率；并通过第三方实验数据验证了在分布不均衡的数据方面，该方法可以取得较好的总体分类以及各类分类效果；

最后笔者将该方法与现有的一些支持向量机(SVM)方法、支持向量数据描述(SVDD)方法进行了比较，结果发现本文方法优于进入对比的各种方法，说明了该方法的可行性和有效性；同时，该方法对滚动轴承故障诊断的研究具有重要的参考价值。