核心问题：提升符号意识的有效支点

焦欢欢

摘要：针对教学结果和过程，以“符号意识”和“核心问题”为观察点，观察苏教版小数数学四年级下册《用数对确定位置》一课。同时，设计前后测试题，在课前和课后对学生进行测试，以确认学生的符号意识是否得到了提升。观察和测试的结果表明：围绕核心问题展开的启发式、探究式、交流讨论式教学，有效地驱动了学生主动使用符号，提升了学生的符号意识。

关键词：符号意识;核心问题;课堂观察;前后测;《用数对确定位置》

一、背景与方法

2021年6月11日，我区展开“学科核心素养与个性化课堂”的教研活动，组织教师对陈老师执教的苏教版小学数学四年级下册《用数对确定位置》一课进行了课堂观察。

数对本质上是一种数学符号。用数对确定位置体现的是符号意识。符号意识是学习者在感知、认识、运用数学符号方面作出的一种主动性反应，更多地表现为一种主动运用符号的意识。《义务教育数学课程标准（2011年版）》指出，符号意识主要体现在：能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理，得到的结论具有一般性。因此，对于教学的结果（目标），笔者以“符号意识”为观察点，重点观察四个方面：理解数对表示的含义;运用数对表示位置和变化规律;使用数对进行运算和推理;理解运用数对得到的结论具有一般性。此外，笔者还基于重点观察的四个方面，设计了两道前后测试题，在课前和课后对学生进行测试（两次测试都用这两道题），以了解学生学习的变化，定量确认学生的符号意识是否得到了提升。具体测试题如下：

1.图1是某校教学楼的平面图。

（1）数对（3，2）表示的是（）班;

（2）四（2）班用数对表示是（，）;

（3）表示某班位置的数对是（4，x），它表示的班级可能是（）;

（4）表示某班位置的数对是（y，y），它表示的班级可能是（）。

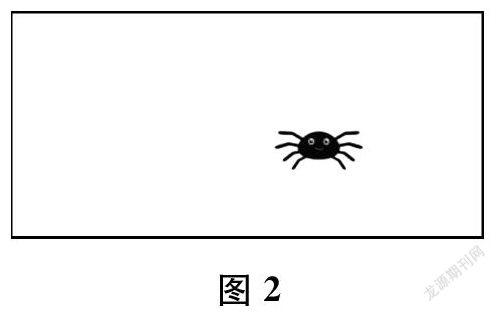
2.如图2，你能准确说出蜘蛛的位置吗？

我想这么做：__________________。

第1大题的（1）（2）两小题考查学生能否理解数对表示的含义并运用数对表示位置;（3）（4）两小题考查学生能否理解数对表示的位置变化规律，以及运用数对得到的结论具有一般性。第2大题则进一步（提高难度）考查学生能否理解数对表示的行列本质并运用数对表示行列特征不明显的位置。

课前了解陈老师的教学设计（方案），发现他尝试围绕以下三个核心问题展开教学：第4列第3行这个说法能不能再简洁一些呢？能不能用一个数对把这一行上的点都表示出来呢？之前接触到的位置表述和本课学习的位置表述有什么联系？“核心问题”是指根据学科本质精心设计的符合学生认知规律的关键性问题、中心性问题，能够引起“牵一发而动全身”的效果，具有指向性、进阶性、关联性的特征。培养符号意识不能靠教师的告知与传授，而要通过问题驱动学生主动使用的心理倾向。因此，对于教学的过程（方法），笔者以“核心问题”为观察点，重点观察以上三个核心问题的教学，定性描述其对学生符号意识培养的作用。

二、观察结果与分析

（一）关于第一个核心问题的教学

第一个核心问题的教学片段如下：

师刚才，按照先说列再说行的规定，我们把小军的位置统一说成第4列第3行。这个说法能不能再简洁一些呢？

[学生回答，出现如下答案：（4，3）、（4.3）、（3，4）、43。]

师都很简洁，你觉得哪种方式好？

生（3，4）不對，因为应该先说列再说行。

生“43”会让人误会是“43”，“（4.3）”会误会是小数。

[交流讨论得出：第4列第3行可以用数对（4，3）表示。]

师结合位置图，数对（3，4）在哪里？

（请学生上台指。）

师看看数对（4，3）和数对（3，4），你有什么想问的？

生都有数字3和4，数对（4，3）和数对（3，4）怎么表示的位置不一样呢？

生数对（4，3）表示第4列第3行，数对（3，4）表示第3列第4行。

生数对的第一个数表示多少列，第二个数表示多少行。

生数在的位置不一样，意思就不一样。

师看来，这里的数对是有序数对，前一个数是列，后一个是行。这其实和计数法的位值制有点像：43表示4个十和3个一，34表示3个十和4个一。

第4列第3行这个说法能不能再简洁一些呢？这个核心问题的指向性很强，指向本节课认知的重难点。教师通过这个核心问题启发学生想到利用符号简洁地表达。由此，学生的思维得到进阶：由准确描述走向简洁描述，由具体位置描述走向抽象数对表达。学生结合具体情境，在交流讨论中明确了符号代表的意义。通过这个核心问题，学生又产生了新的问题：数对（4，3）和数对（3，4）怎么表示的位置不一样呢？进而将（4，3）和（3，4）对比，进一步理解符号表示的含义，以及不同符号之间的区别和联系。

（二）关于第二个核心问题的教学

第二个核心问题的教学片段如下：

[教师依次说出数对（1，5）、（2，5）、（3，5）、（4，5）、（5，5）、（6，5），学生相机在黑板上放上磁贴。]

师那（7，5）呢？

生老师，我发现你放的规律了，都放在第5行上，列数每次都加1。

师照这个规律放下去，放得完吗？

生放不完。

师你能不能用一个数对把这一行上的点都表示出来呢？

生（1—6，5）。

生不行，这只表示了1到6列，可以写成（n，5），用字母n表示任意一列，但是第二个数必须是5，因为都是在第5行。

师（n，5）表示第5行上的任意一点。现在请一位同学做“小老师”，说数对，让大家来指。

生指出数对（3，n）。

生可以是（3，1）、（3，2）、（3，3）、（3，4），就是第3列上的任意一点。

师同学们，如果要表示平面上的任意一点呢？你会表示吗？

生（n，n）。

生不行，如果n=1，就是数对（1，1）;n=2，就是（2，2）。

师（在黑板上画图）老师来把符合这一规律的数对表示出来，你有什么发现？

生是一条线上的点。

生那就用两个不一样的字母：（x，y）。

师的确，数对的作用可真大，不仅可以描述一个点的位置，还可以描述一条线甚至一个面上所有点的位置。

能不能用一个数对把这一行上的点都表示出来呢？这个核心问题启发学生进一步想到：能用一个数对把这一列上的点都表示出来吗？能用一个数对把这个面上的点都表示出来吗？学生的思维逐步由点向线、向面进阶。这里，学生的表现表明：他们已经逐步学会运用符号表示一个点的位置、一条线甚至一个面上所有点的位置。也就是说，学生不仅能用符号表示位置，而且能用符号表示位置变化规律。可见，学生的符号意识在逐步深化。

（三）关于第三个核心问题的教学

第三个核心问题的教学片段如下：

师之前接触到的位置表述和本课学习的位置表述有什么联系？

生二年级课本上，位置表述用的是东、南、西、北、东南、东北、西南、西北这样的方位词。

生以前学习的方法表述的是大概的一块区域，今天学习的数对表述的是一个点。

师有了列与行的数，就能更精确地确定位置。看来，用数说形很精确。

生我不仅在课本上学习过确定位置，而且在电影院中看到过第几排第几座的位置表述。

……

师（课件呈现图3）生活中的确定位置和本课中的确定位置相比，有什么共同点？

生都用了数列与行的办法来确定位置。

生都用了数或字母符号来表示。

师是的，用数对这样的符号能精确地表述位置。作用可真大啊！

之前接触到的位置表述和本课学习的位置表述有什么联系？这个核心问题唤醒了学生的已有经验，即二年级学习的用方向表示位置。教师启发学生比较，讓学生感受到用数对这一符号表示的精准和简洁，凸显了符号的价值。而学生又自觉地将生活中接触到的位置表述与本课学习的位置表述进行对比，从而感受到内在的一致性。由此，学生开始用符号的眼光去观察车票、棋盘、电影院座位图等中的数或字母的意义，进一步发展了符号意识。

三、前后测结果与分析

全班48位学生两道题前后测的正确率分别如图4、图5所示。

由此可见，经过这节课的教学，学生后测的正确率相比于前测都有了较大幅度的提升，尤其是第1大题的（3）（4）两小题和第2大题。这说明，学生的符号意识有了明显的提升，尤其是在理解数对表示的位置变化规律以及运用数对得到的结论具有一般性方面，还有理解数对表示的行列本质并运用数对表示行列特征不明显的位置方面。

综合课堂观察和前后测结果，可以得出结论：围绕核心问题展开的启发式、探究式、交流讨论式教学，有效地驱动了学生主动使用符号，提升了学生的符号意识。换句话说，核心问题成为提升学生符号意识的有效支点。

参考文献：

[1] 王光明，范文贵.新版课程标准解析与教学指导·小学数学[M].北京：北京师范大学出版社，2012.

[2] 杨海燕.基于前后测的课例研究——以《周长》为例[J].教育研究与评论（课堂观察），2021（1）.

[3] 吴晓亮.学习活动形式如何有效——《确定位置》课堂观察报告[J].教育研究与评论（课堂观察），2017（1）.