Effects of dipolar interactions on the magnetic hyperthermia of Zn0.3Fe2.7O4 nanoparticles with different sizes*

Xiang Yu(俞翔), Yan Mi(米岩), Li-Chen Wang(王利晨), Zheng-Rui Li(李峥睿),Di-An Wu(吴迪安), Ruo-Shui Liu(刘若水), and Shu-Li He(贺淑莉)

Department of Physics,Capital Normal University,Beijing 100048,China

Keywords: magnetic nanoparticles,dipolar interaction,magnetic hyperthermia

1. Introduction

Magnetic hyperthermia is a new type of flexible and controllable local tumor hyperthermia method, which has attracted much attention in recent years. Magnetic NPs are leading candidates for medical applications because of their unique multifunctional properties. Because the temperature tolerance of tumor cells is worse than that of normal cells,we can selectively kill tumor tissue by heating tumor tissue area to 42◦C–46◦C under the premise of maximum protection of normal tissue.[1–7]The specific loss power (SLP) is generally used to evaluate the heating performance of magnetic NPs under an AC field. In the previous reports, many studies focused on the Fe3O4NPs, and obtained the highest SLP value of 2452 W/gFein cubic Fe3O4NPs under the AC field of 520 kHz and 29 kA/m.[8]Recently, Cheno et al. fabricated core–shell Zn0.4Co0.6Fe2O4@Zn0.4Mn0.6Fe2O4with soft-hard magnetic exchange coupling, obtained SLP of 3886 W/g.[9]Our group reported soft-hard mixed ferrite NPs of Co0.03Mn0.27Fe2.7O4with SLP of 3417 W/gmetal.[10]However,improving the heating performance of magnetic NPs has been always a hot topic in the field of magnetic hyperthermia.

It is well known that the heating ability of NPs depends on not only intrinsic magnetic properties, such as the saturation magnetization and magnetocrystalline anisotropy,but also extrinsic properties,such as NP size,shape,and assemble.Recently,it was reported that the dipole interaction between magnetic NPs also has a non-negligible influence on hyperthermia performance.[11–15]It has been reported that the dipole interactions can improve the heating performance of superparamagnetic NP columns by generating an additional magnetic uniaxial anisotropy, which is favored by lower particles’ individual anisotropy and longer column.[16]It was suggested that the optimal individual anisotropy should shift to the lower value when dipole interactions increase the effective magnetic anisotropy of chain clusters and the optimal value of individual anisotropy increases with damping factor.[17]Dipole interactions are inclined to improve the hyperthermia heating only when the clusters are small enough to induce an enhancement in clusters’shape anisotropy.Once the clusters are losing their shape anisotropy,dipole interactions will change to impair the heating.[18]Therefore, effect of dipolar interaction between NPs on magnetic hyperthermia is worth investigating.

In this paper, we prepared Zn0.3Fe2.7O4magnetic NPs with different sizes by a modified thermal decomposition method. Then the SiO2shell were coated on the surface of NPs, which can make NPs water soluble and biocompatible.The dipolar interaction between NPs was tuned by changing the solution concentration. We investigate the solution concentration dependence of magnetic hyperthermia perfomance of Zn0.3Fe2.7O4/SiO2aqueous solution, and effects of dipolar interaction between magnetic NPs on heating ability was discussed.

2. Experimental details

Zn0.3Fe2.7O4magnetic NPs were prepared by the modified thermal decomposition method. 2.7 mmol of Fe(acac)3,0.3 mmol of Zn(acac)2·nH2O,2 mmol of sodium oleate,a certain amount of oil acid and 20 ml of benzyl ether were mixed in a flask. The solution was heated to 120◦C and maintained for 0.5 h. Then, the mixture was heated up to 295◦C and refluxed for 2 h,then cooled down to room temperature by removing the heating mantle. Finally,the NPs were precipitated with ethanol.

The size of NPs can be tuned by controlling the dosage of oleic acid. For example, adding 5-mL, 4.7-mL, 4.4-mL, and 4.2-mL oleic acid to the reaction system, magnetic NPs with sizes of 14 nm, 16 nm, 18 nm, and 20 nm can be obtained respectively.

For silica coating with a thickness of 6 nm, 20 mL of cyclohexane and 1.15 mL of Igepal CO-520 were mixed and 20 mg of magnetic NPs in 1 mL of cyclohexane were added while magnetic stirring. 0.15-mL ammonium hydroxide(29%)was added,followed by 0.1-mL TEOS.The solution was stirred at room temperature for 24 h and the NPs were precipitated with hexane.

The morphology of NPs was observed by transmission electron microscope (TEM, Hitachi H-7650). The crystal structure was characterized by x-ray diffraction(XRD,Bruker D8 advanced). The elemental compositions of the samples were measured by Inductively coupled plasma atomic emission spectroscopy(ICP-AES,IRIS ADVANTAGE).The room temperature magnetic properties were measured by Vibrating sample magnetometer(VSM,Microsense). The magnetic hyperthermia properties were measured by MSI HYPER 5 machine.

3. Results and discussion

The powder x-ray diffraction patterns of Zn0.3Fe2.7O4magnetic NPs with sizes of 14 nm to 20 nm were measured,to determine the crystal structure of the samples,as shown in Fig.1. All the peaks are all in good agreement with the standard PDF card#86-0510,confirming a cubic phase structure of all the samples. Inductively coupled plasma atomic emission spectroscopy (ICP-AES) was used to measure the elemental compositions of the Zn0.3Fe2.7O4NPs. The atomic ratio of Zn:Fe was detected to be 0.2:2.8 in the series samples, close to stoichiometric composition of Zn0.3Fe2.7O4NPs.

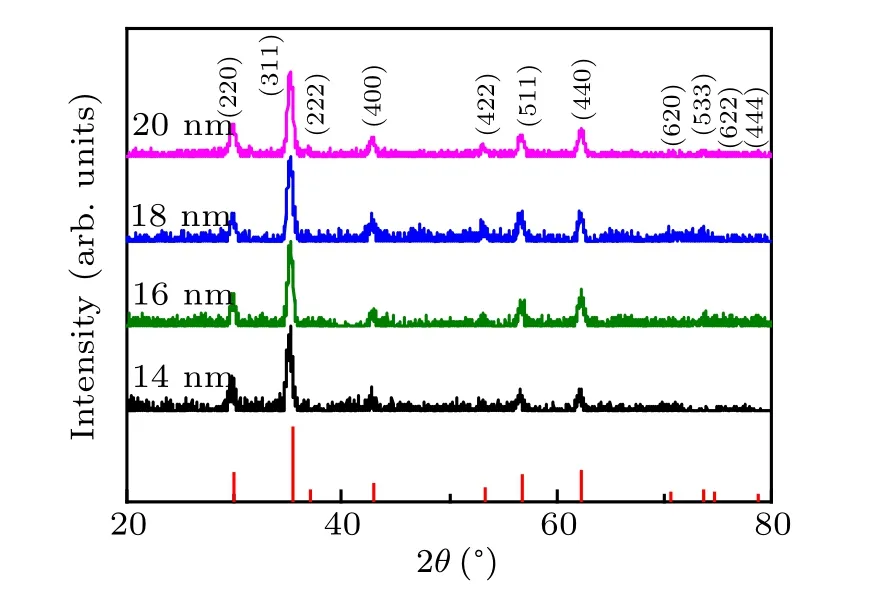
Fig. 1. XRD patterns of Zn0.3Fe2.7O4 magnetic NPs with sizes of 14 nm,16 nm,18 nm,and 20 nm.

Fig.2. TEM image and size distribution of Zn0.3Fe2.7O4 magnetic NPs with different sizes[(a)and(e)]14 nm,[(b)and(f)]16 nm,[(c)and(g)]18 nm,[(d)and(h)]20 nm.

Magnetic NPs with controllable size and morphology can be synthesized in one step, by the modified thermal decomposition method. In our experiment, the oleamine and 1,2-hexadecanediol used in the classical method were replaced by sodium oleate.[19]Figures 2(a)–2(d) are the TEM images of Zn0.3Fe2.7O4NPs with average size of 14 nm to 20 nm respectively, and figures 2(e)–2(h)are histograms of the size distribution series. It can be seen that the Zn0.3Fe2.7O4series magnetic NPs have characteristics of regular morphology,narrow size distribution and good mono-dispersity. As the amount of oleic acid decreased from 5 mL to 4.2 mL,the synthesized NPs size gradually increased from 14 nm to 20 nm, realizing the tune of NP size. This is mainly due to the fact that oleic acid, as the growth rate controller,can adjust the process of monomer formation of nanocrystals.

The SiO2coating make NPs water soluble and biocompatible.Figures 3(a)–3(d)are TEM images Zn0.3Fe2.7O4/SiO2NPs with magnetic core of 14 nm to 20 nm respectively. It can be seen that the Zn0.3Fe2.7O4/SiO2series composite are coated uniformly without free SiO2shell, and the shell thickness is about 6 nm.

Fig.3.TEM image of Zn0.3Fe2.7O4/SiO2 composite NPs with different magnetic core sizes of(a)14 nm,(b)16 nm,(c)18 nm,and(d)20 nm.

The room temperature magnetic properties of Zn0.3Fe2.7O4NPs with different sizes were measured by VSM, and the result is shown in Fig. 4. Hysteresis loops indicated Zn0.3Fe2.7O4NPs are superparamagnetic at room temperature. The saturation magnetization(Ms)of the sample gradually raises from 77 emu/g to 87 emu/g with the NP size increasing from 14 nm to 20 nm. The increase of Mscan be attributed to the reduced surface spin with increasing NP size.

Figures 5(a)–5(d)are heating curves of aqueous solution of Zn0.3Fe2.7O4/SiO2NPs with core size from 14 nm to 20 nm at different concentrations. Zn0.3Fe2.7O4/SiO2with different solution concentration respectively. The temperature rising of aqueous solution were recorded by optical fiber temperature probe within 180 seconds. Temperature rising increase monotonously with increasing solution concentration. However, dosage of NPs is expected as low as possible in clinical therapy to minimize the cytotoxicity of NPs.

Fig.4. (a)M–H curves of Zn0.3Fe2.7O4 magnetic NPs with sizes of 14 nm,16 nm, 18 nm, and 20 nm at room temperature and (b) Ms versus NP size.The unit 1 Oe=79.5775 A/m.

The heating ability of magnetic NPs under an AC field is expressed by the specific loss power (SLP) which provides a measure of the rate at which energy is absorbed per unit mass of the magnetic NPs when exposed to an AC field. The equation of SLP is described as

where C is the volume specific heat capacity, Vsis the volume of the sample, m is the mass of the metallic elements of the NPs in the sample, dT/dt is the initial slope of the temperature rise curve. Figure 6 is the solution concentration dependence of SLP value for Zn0.3Fe2.7O4/SiO2with different sizes under an AC field of 430 kHz and 27 kA/m. The highest SLP values of NPs can reach 451 W/gmetal, 766 W/gmetal,1343 W/gmetal, and 2072 W/gmetalat the concentration of 5 mg/mL, 1 mg/mL, 0.5 mg/mL, and 0.2 mg/mL for 14 nm,16 nm, 18 nm, and 20 nm NPs respectively. As NP size increases, the position exhibiting maximum SLP value moves to the direction of low concentration. In particular, for the sample with a magnetic core of 20 nm, it can be deduced that the peak value should be expected to appear in the lower concentration.[20]

Fig. 5. Heating curves of aqueous solution of Zn0.3Fe2.7O4/SiO2 NPs with core sizes of (a) 14 nm, (b) 16 nm, (c) 18 nm, and (d) 20 nm at different concentrations under an AC field of 430 kHz and 27 kA/m.

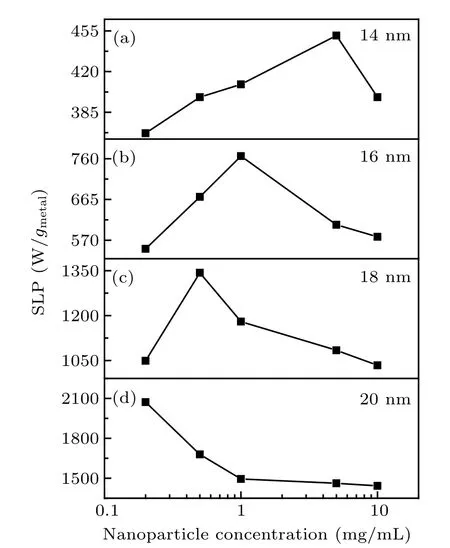
Fig. 6. SLP values dependence on the NP concentration for Zn0.3Fe2.7O4/SiO2 with different sizes: (a) 14 nm, (b) 16 nm, (c) 18 nm,(d)20 nm under an AC field of 430 kHz and 27 kA/m.

When magnetic NPs were exposed in AC magnetic field,NPs will be heated due to the conversion of electromagnetic energy into heat. The power dissipation can be described as

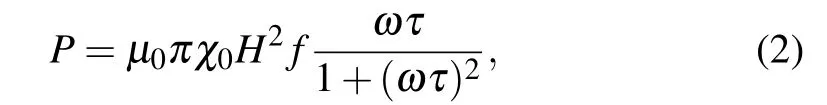
where τ is the total relaxation time of the magnetic NPs under the AC field, μ0is the vacuum permeability, χ0is the equilibrium susceptibility, H is the amplitude of the AC field and f is the frequency of the AC field (f =ω/2π). It can be seen that when external parameters including the magnitude and frequency of the AC field are fixed,what determines the loss power are the DC susceptibility and relaxation time τ. From Eq. (2) it can be shown easily that maximum P occurs at ωτ =1.[21–24]For superparamagnetic NPs with low anisotropy,the field and temperature dependent magnetization obeys Langevin function, from which we can obtain that is proportional to the saturation magnetization. It can be found from Fig.6 that SLP values increase obviously with increasing NP size,which results from significant increase of magnetization.

Rosenweig proposed that the relaxation of superparamagnetic NPs is contributed by N´eel relaxation and Brownian relaxation.[21]N´eel relaxation refers to the reversal of the magnetic moment of NPs,and is described by equation where τ0is the time constant(τ0～10-9s);K is the anisotropy constant;and V is the volume of NP.

Brownian relaxation is related to the physical rotation of the NPs,and is given by

where η is the viscosity coefficient of the magnetic fluid;VHis taken as the hydrodynamic volume of the NP;kBis the Boltzmann constant and T is the absolute temperature.

The total relaxation is given by

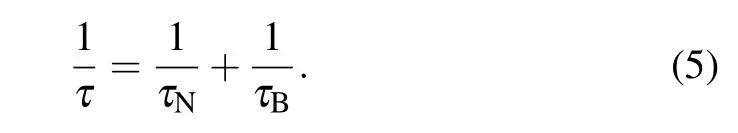
In free suspensions, interparticle interactions can be observed experimentally.[25]The dipolar interactions between adjacent particles favor their assembly into chains, inducing shape anisotropy. The strength of dipolar interactions is inversely proportional to the third-order of distance between magnetic cores. The distance between NPs can be tuned by varying the concentration of solution. Dipolar interaction between NPs was studied extensively. Martinez-Boubeta et al.studied the SLP values of Fe–MgO NPs with different concentrations and sizes, and found that there was a non-monotonic relationship between SLP values and concentrations. Through numerical simulation,it is found that the SLP value increases with the increase of the concentration of NPs until the magnetic interactions between NPs become comparable to the anisotropy field. When the concentration of NPs is further increased, the magnetic interaction between NPs will increase significantly,resulting in the decrease of SLP value.[20]Landi verified the above research results via numerical simulation based on a mean-field model. The theoretical simulations predicted that the SLP value increases first and then decreases with the increase of solution concentration.[12]Tan et al. also found the magnetic interaction will increase with the increase of the concentration of NPs by theoretical simulation. For the 9-nm and 20-nm NPs, the magnetization value at 40 mT shows a monotonic decrease with the increasing of concentration. On the other hand, the coercive field increases first and then decreases with the increasing NPs concentration. Therefore,the overall change process is an increases in energy loss followed by a decrease. With the concentration of magnetic NPs increases,the hysteresis loop under the AC field gradually changes from the major loop to the minor loop,leading to the decrease of energy loss with increasing concentration.[26]The maximum energy loss occurs in a certain appropriate range.The dipolar interaction between NPs affects both coercivity field and magnetization,and finally,reflects in area of hysteresis loop. The appropriate concentration of NPs will make the hysteresis loop have the maximum area under the AC field,and thus produce the highest SLP value.

4. Conclusion

Zn0.3Fe2.7O4magnetic NPs with sizes of 14 nm, 16 nm,18 nm, and 20 nm were prepared by the modified thermal decomposition method. By using the reverse microemulsion method, SiO2shell layers were coated on the surfaces of NPs to prepare magnetic fluid samples with different concentrations. The results show that series Zn0.3Fe2.7O4magnetic NPs all have a single cubic phase structure and superparamagnetism at room temperature. The SLP value of Zn0.3Fe2.7O4/SiO2NPs smaller than 20 nm changes nonmonotonically with the concentration of solution under the AC magnetic field of 430 kHz and 27 kA/m. SLP values of all Zn0.3Fe2.7O4/SiO2NPs appear a peak value with change of solution concentration. The solution concentration with optimal SLP value decrease with increasing magnetic core size.The results of this study are expected to provide effective guidance strategies for the application of magnetic NPs of different sizes in clinical magnetic hyperthermia.