永磁同步电机新型无差拍直接转矩控制

扶文树 ，储建华 ，王刚

（1.南京信息职业技术学院智能制造学院，江苏 南京 210036；2.江苏开璇智能科技有限公司，江苏 苏州 215101）

永磁同步电机具有效率高、功率密度高、转矩脉动小、调速范围宽等优点，对其通常采用磁场定向控制[1]（field oriented control，FOC）和直接转矩控制[2]（direct torque control，DTC）。传统的直接转矩控制无需内环电流控制即可实现转矩和磁链的控制，具有动态特性好、参数变化鲁棒性强的特点。然而，传统的直接转矩控制系统由2个非线性磁滞比较器和一个由6个控制电压矢量组成的开关表组成。电压矢量在每个采样周期开始时变化，每个逆变器的状态以可变的频率变化，因此存在开关频率不固定及转矩、磁链波动明显的缺点[3]。此外，逆变器的死区、电机参数的非线性变化也会引起系统波动，限制了直接转矩控制在永磁同步电机中的实现。

针对以上不足，研究者们研究了空间矢量调制（space vector modulation，SVM）直接转矩控制[4]、模型预测控制[5]（model predictive control，MPC）和占空比调制控制[6]。无差拍直接转矩控制（deadbeat direct torque control，DBDTC）将经典PI控制结构和空间矢量脉宽调制与直接转矩控制相结合，基于永磁同步电机模型的离散方程，计算并应用下一采样时间的电压矢量[7-8]，其保持了传统DTC的快速动态特性和支持向量机的恒定切换频率。另外，电机的内部参数如定子电阻、电感以及转子磁链随运行过程中温度的变化而变化，该参数摄动会引起无差拍直接转矩控制中给定电压空间矢量的变化，影响转矩和磁链控制的性能，有效的扰动观测和参数辨识对于无差拍控制的鲁棒性是必要的。

针对上述问题分析，本文提出了一种基于滑模扰动观测器补偿的永磁同步电机无差拍直接转矩控制策略。首先，结合滑模控制理论，构建了dq轴滑模扰动观测器，对参数摄动引起的轴电压变化量进行观测，将其补偿至给定轴电压，提高系统对参数摄动的鲁棒性。在此基础上，对定子电阻和电感值进行离线辨识。其次，对q轴滑模扰动观测器进行了重构，在对q轴参考电压扰动补偿的同时对转子磁链进行了有效辨识。试验结果证明本文提出控制策略的有效性。

1 基于滑模扰动观测器的无差拍控制

无差拍直接转矩控制的d，q轴参考电压给定与定子电阻R、电感L以及转子永磁体磁链Ψf相关。考虑到电机运行过程中的温度变化，以上三种电机参数会发生摄动，因此，需分别对无差拍控制中三种电机参数摄动造成的系统扰动进行观测并有效补偿。

1.1 基于扰动观测器的参数辨识

根据d-q旋转坐标系下的永磁同步电机数学模型，若考虑电机实际运行过程中的定子电阻R、电感L以及转子永磁体磁链Ψf摄动量ΔR，ΔL和ΔΨf引起的系统扰动，d-q旋转坐标系下的永磁同步电机电压方程可改写为

其中

式中：ud，uq分别为电机定子d，q轴电压分量；id，iq分别为电机定子d，q轴电流分量；R为定子电阻；ω为转子电角速度；fd，fq为参数摄动引起的d，q轴电压变化量。

构建滑模扰动观测器为

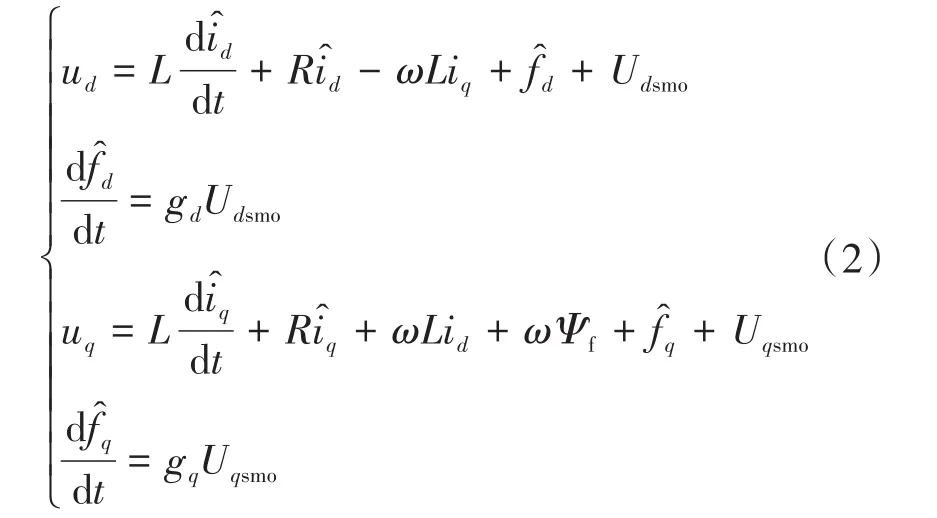
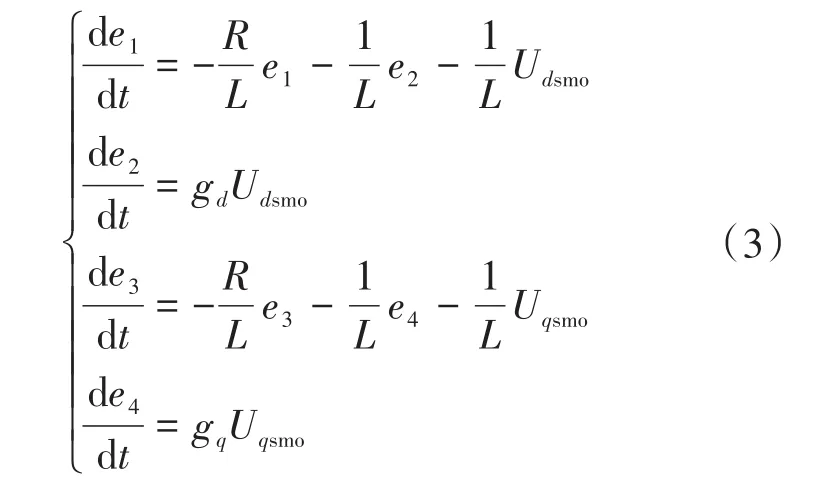
其中

式中：e1，e3为d，q轴电流估计误差；e2，e4为d，q轴扰动估计误差。

选取如下滑模面：

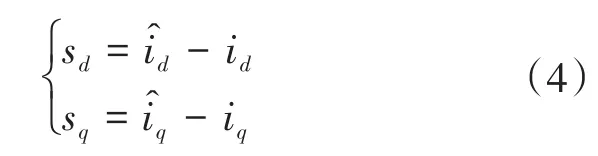
为提高滑模扰动观测器的观测准确性，选取等速趋近律为

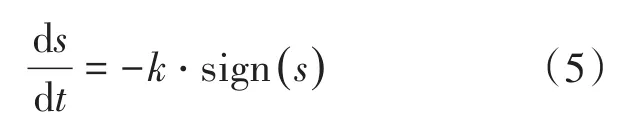
式中：k为趋近律系数。

将式（4）代入式（5），得到：

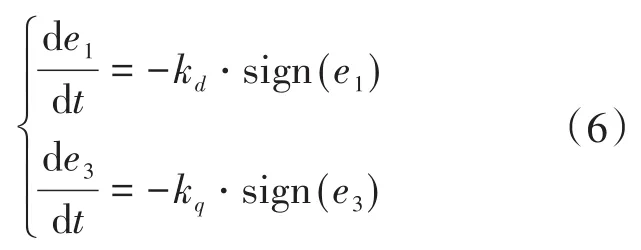
式中：kd，kq分别为d，q轴趋近律系数。将式（3）入式（6），得到：

对式（7）求解，得到控制函数为

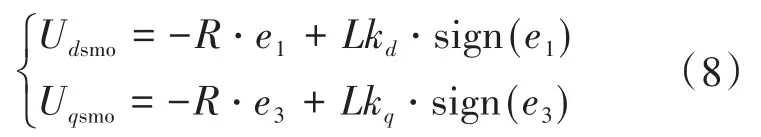
为保证滑模系统的收敛性，选取滑模参数kd，kq和gd，gq需满足：

对式（9）求解，得到：

当系统进入滑动模态，式（3）简化为

对式（11）求解，得到：

对式（2）离散化处理，得到：

式中：Ts为系统电流控制周期。

根据式（13）、式（14）构建的离散型扰动滑模观测器，可观测出参数摄动引起的d，q轴电压变化量，将其补偿到d，q轴参考电压给定得到最终d，q轴参考电压给定为

当系统进入滑动模态，参数摄动引起的d，q轴电压变化量简化为

根据式（16）中表达式，可得电感参数辨识，根据表达式，给定两次iq值，可得电阻参数辨识，即

式中：L0，R0为电感、电阻参数辨识值；iq1，iq2为两次给定iq下的q轴实际电流；ω1，ω2为两次给定iq下的转子电角速度为两次给定iq下的q轴电压变化量估计。

综上，基于扰动滑模观测器的参数辨识原理框图如图1所示。

图1 基于扰动滑模观测器的参数辨识框图Fig.1 Block diagram of parameters identification based on disturbance sliding mode observer

1.2 基于扰动补偿的无差拍控制

根据电机输出电磁转矩方程，转子永磁体磁链Ψf的准确性对电机控制性能影响较大，因此，需重新构建q轴扰动滑模观测器，对其进行相应辨识。

假定只考虑电感参数摄动，式（1）可改写为下式：

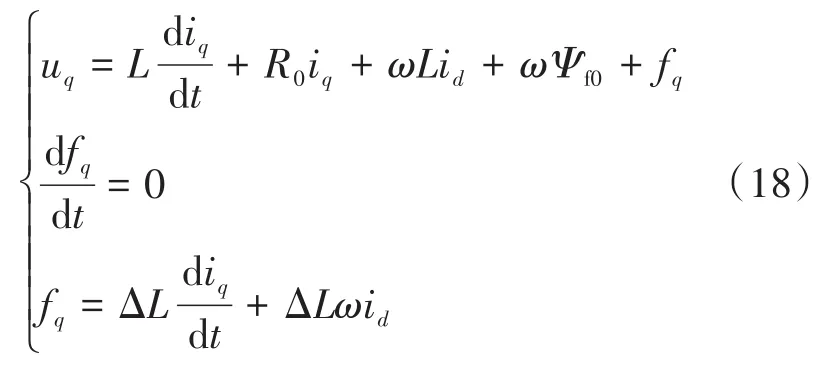
重构q轴扰动滑模观测器为

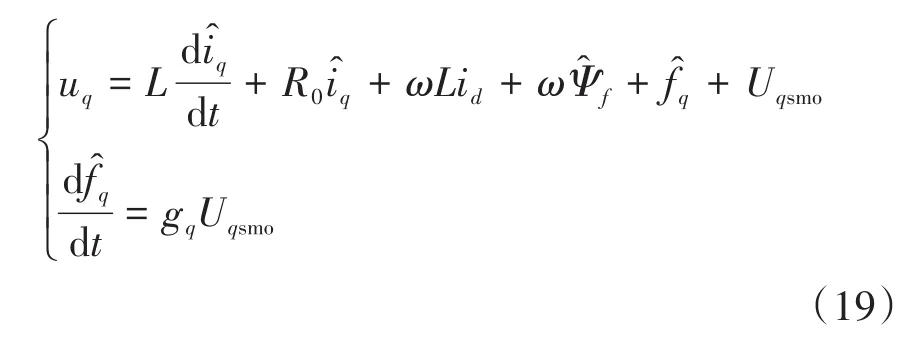
将式（18）与式（19）相减，得到：

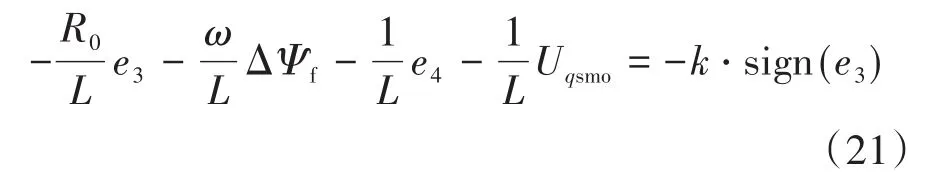
其中

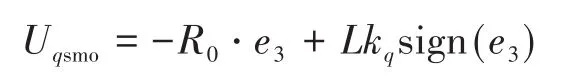
为保证滑模系统收敛性，需满足如下条件：

对式（22）求解，得到：

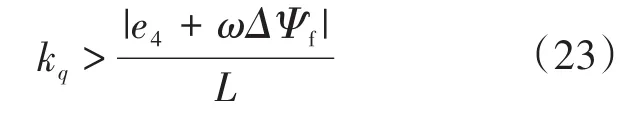
当滑模系统收敛时，式（20）可简化为

即

由式（25）可知，为使e4收敛，需满足gq＞ 0。因此，合理选取kq,gq大小，可保证q轴扰动滑模观测器的稳定性。

对式（26）求导，得到：

对式（24）求解，得到：

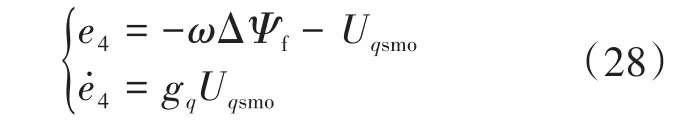
将式（28）代入式（27）中，得到：

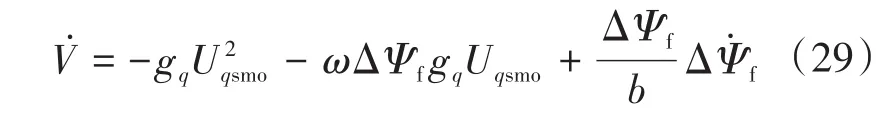
分析式（29）可知，由于gq＞0，则要使＜ 0，需满足：

整理式（30），得到：

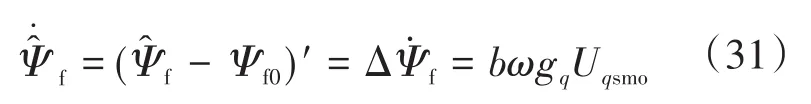
最终与式（19）重构q轴扰动滑模观测器联立可辨识出转子永磁体磁链。

综上，基于扰动滑模观测器补偿的无差拍直接转矩控制原理框图如图2所示。

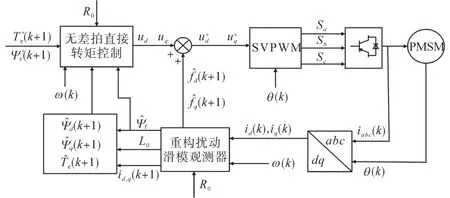
图2 基于扰动滑模观测器补偿的无差拍直接转矩控制框图Fig.2 Deadbeat direct torque control block diagram based on disturbance sliding mode observer compensation

2 试验研究

在永磁同步电机交流调速试验平台上，将本文提出的基于扰动滑模观测器补偿的无差拍直接转矩控制策略与传统直接转矩控制作对比试验，对应的试验电机参数如下：额定功率PN=400 W，额定电压UN=220 V，额定电流IN=2.6A，额定转矩TN=1.2 N·m，额定转速nN=3000 r/min，定子电阻R=2.3Ω，定子电感L=7.34mH，转子磁链Ψf=0.122 Wb，电机极对数p=4。

试验过程包括动态试验和稳态试验。

在图3为给定负载转矩突变下的电磁转矩响应波形，给定电机1 000 r/min的转速值，在0～1.5 s时间段通过测功机给定1.2 N·m的负载转矩，在1.5 s～3.0 s时间段负载转矩突变至0.3 N·m，在3.0 s～4.5 s时间段再次突变至1.2 N·m。其中，图3a为传统直接转矩控制下的响应波形，图3b为基于扰动滑模观测器补偿的无差拍直接转矩控制下的响应波形，对比图3a与图3b可以看出，基于扰动滑模观测器补偿的无差拍直接转矩控制保持了传统直接转矩良好的转矩动态性能，在此基础上，转矩纹波系数大幅度降低，由原先的25%降低至14%。

图3 给定负载突变下的电磁转矩Fig.3 Electromagnetic torque under given abrupt load change

图4～图6分别为给稳态下的转速、电磁转矩和定子磁链对比试验波形，稳态条件给定电机2 000 r/min的转速值以及1.2 N·m的负载转矩。

图4 稳态下的转速Fig.4 Steady-state speed

图5 稳态下的电磁转矩Fig.5 Steady-state electromagnetic torque

图6 稳态下的定子磁链Fig.6 Steady-state stator flux linkage

对比图由图4～图6可知，基于扰动滑模观测器补偿的无差拍直接转矩控制稳态下的转速脉动由25%降低至5%，电磁转矩和磁链脉动大幅度降低，由此验证了基于扰动滑模观测器补偿的无差拍直接转矩控制的有效性。

图7为两种控制策略下的电机启动过程转速响应波形。

图7 启动过程转速响应波形Fig.7 Speed response waveform in starting process

根据图7a可以发现，传统DTC控制策略下的电机转速存在180 r/min左右的超调，经过大约5 ms左右的调节时间达到稳态值。并且其在启动与稳态过程中存在较大的转速波动。对比图7b中的SMDO-DBDTC控制可知，SMDO-DBDTC控制策略下的转速超调仅仅为10 r/min左右，无明显转速波动。

3 结论

本文针对传统无差拍直接转矩控制中电机内部参数摄动对给定电压矢量的影响，提出了一种基于滑模扰动观测器补偿的永磁同步电机无差拍直接转矩控制策略。

首先，结合滑模控制理论，构建了d，q轴滑模扰动观测器，对参数摄动引起的d，q轴电压变化量进行观测，将其补偿至给定轴电压，提高系统对参数摄动的鲁棒性。在此基础上，对定子电阻和电感值进行离线辨识。

其次，对q轴滑模扰动观测器进行了重构，在对q轴参考电压扰动补偿的同时对转子磁链进行了有效辨识。试验对比传统直接转矩控制与本文控制策略，结果验证了本文提出控制策略的有效性和可行性。