转子分段斜极永磁同步电机电磁振动噪声研究

王玉娟，王华强

（1.山东华宇工学院电气工程学院，山东 德州 253034；2.合肥工业大学电气与自动化工程学院，安徽 合肥 230009）

永磁同步电机（PMSM）因其结构紧凑、功率密度高，被广泛应用于电动汽车（EV）[1]。然而与传统汽车相比，由于车辆噪声激励源的变化，电机驱动的车辆呈现出新的噪声特性，且在这种情况下高频噪声的急剧增加尤为明显[2]。此外，这些高频噪声中的一部分分布在对人耳敏感的频率范围内，从而导致驾驶员和乘客感觉非常不适[3-4]。因此，研究车辆PMSM的噪声特性对于降低噪声和改善电动汽车的音质具有重要意义[5]。

电磁激励是电磁噪声的根源。具体地，径向磁力主要作用在定子齿表面上，并呈现出气隙中的时空磁分布特征。不同频率的空间阶数和可变形幅度直接影响电磁噪声分布[6]。同时切向磁力分量产生与电磁转矩相对应的作用力矩，导致齿根的弯曲振动，然后引起转矩波动[7]。目前，对永磁同步电机噪声特性的研究主要分为两类：一是分析来自于激励源的电磁噪声的分布特征，如电流-时间的谐波调制、气隙的磁控制和磁力的时空分布；二是研究电磁噪声阶次特征，寻找通过阶次特征来削弱电磁噪声的方法[8]。

本文建立了一种能够进行电磁噪声预测的多物理场仿真模型，分析了转子分段斜极对电磁噪声分布的影响。首先，在构建电机模型的基础上，分析了影响电磁噪声的转子分段斜极模型，研究了低阶径向磁力的频谱特性。其次，将径向磁力加载到定子齿面上，然后采用模态叠加法进行电机的振动响应分析。最后，模拟了整机的辐射噪声，通过进行电机辐射噪声实验，验证了本次建立的模型在预测和评估电磁噪声方面的有效性。

1 构建基于多物理场仿真模型

研究PMSM的电磁振动噪声需要从电磁场、位移场、应力场等多个物理场进行分析，因此本文构建了基于多物理场的仿真模型。首先进行电机磁场分析，计算获取电机的磁场和磁通分布；然后通过位移场分析，了解径向力密度的幅度在不同时间和位置处的变化情况，计算获得不同圆周位置的径向磁力以及不同斜极角情况下径向磁力的变化情况；最后在应力场情况下进行结构分析，对电机定子、绕组耦合情况进行振动模态分析，判断电机的机械性能。

1.1 PMSM的结构建模

PMSM主要由转子铁心、永磁铁、定子铁心、绕组、壳体、前后端盖和转子轴组成。在电机的有限元建模中，应考虑电机组件各部分之间的实际接触状态，并且应仔细检查关键结构的有限元网格[9]。其中，端盖通过刚性元件与机体连接，绕组与定子，定子和壳体之间的接触状态由节点耦合决定。由于转子铁心不直接与定子和壳体接触，当转子在稳定状态下具有稳定的电磁转矩时，它可以等效地模拟为均匀加载到转子轴表面上的质量块。因此，在结构有限元建模中，转子铁心和永磁体被简化为加载到转子轴表面上的质点。图1为PMSM有限元模型。

图1 PMSM有限元模型Fig.1 Model of PMSM finite element

径向磁力是电磁噪声的激发源，它作用于气隙中定子的齿面使电机振动，然后向周围的空气辐射噪声[10]。转子分段斜极磁铁可以有效地削弱定子齿谐波，并减小转矩脉动，从而提高电机输出转矩的稳定性。本次研究通过比较有无分段斜极情况下径向磁力的特性，来研究斜极角对电磁噪声的影响。

图2为分段斜极转子结构。

图2 分段斜极转子结构Fig.2 Structure of segmented oblique pole rotor

1.2 多物理场仿真模型

图3为多物理场仿真模型，主要实现对PMSM振动、噪声的预测。其中包括电磁分析、三维模型分析、频率响应分析及噪声辐射分析。在具有转子分段斜极的PMSM的电磁分析中，每个气隙部分的电磁特性是不同的，因为每个斜极转子在沿圆周方向上具有不同的斜极角。为了从整机的角度评估具有不同斜极角的永磁同步电机的振动特性，需要将模拟结果与实验结果进行对比分析。

图3 多物理场仿真模型Fig.3 Multiphysics simulation model

2 电磁分析

2.1 磁通分布

本次选择的电机为内置式PMSM，其主要设计参数如下：相/极/槽3/8/48，气隙长度0.602 mm，开口宽度2 mm，额定速度3 980 r/min，电流幅度268 A，电流角度39.2°，定子外径220 mm，定子内径143.2 mm，电机内径48 mm，转子轴向长度148.8 mm，倾斜角度2.5°。其中，永磁材料为35UH_80C，相对磁导率为1.03，电导率为635000S/m。电机由正弦波电流供电，基本频率为265.33 Hz，图4为额定速度下磁通分布负载图，可以看出在气隙中，磁通线沿圆周方向密集分布并具有明显的周期性，而在圆周空间中，磁通线的不均匀分布是电磁振动和噪声的主要来源。

图4 额定速度下的磁通分布负载Fig.4 Magnetic flux distribution load at rated speed

2.2 磁力计算

2.2.1 不同圆周位置的径向磁力

在气隙中，因为磁通密度呈周期性分布，从而导致径向力密度将随时间、空间变化。径向力密度的幅度在不同的时间、位置不断变化，径向磁力的不均匀分布将导致电磁噪声。下式为径向磁力密度计算公式：

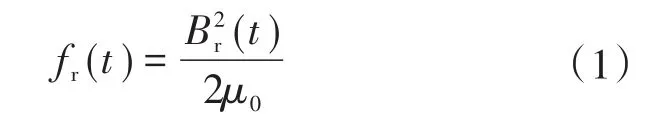
式中：fr（t）为径向力密度；Br（t）为径向通量密度；μ0为真空渗透率。

图5为不同位置处的径向力密度的光谱分布，其中“距离”是指相对于给定时间主磁轴在定子、转子之间重合位置的圆周距离。图5中，通过4条模拟曲线给出了不同圆周位置的径向力密度分布特征，结果表明径向磁力密度的频域分布在不同的圆周位置是相似的，并且径向力幅度主要集中在4 000 Hz以下。通过对整个圆周上的径向力密度进行积分和求和，可以计算单位轴向距离Fn的径向磁力。

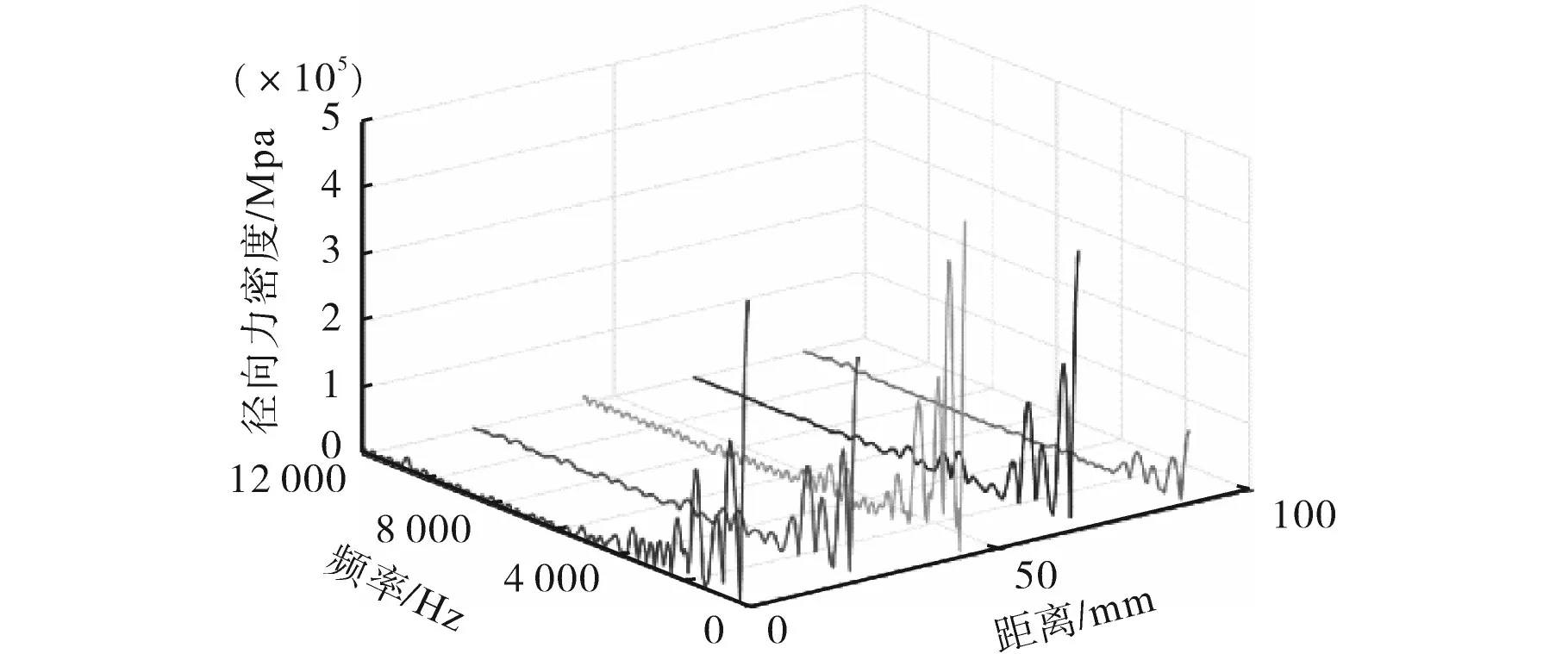
图5 沿圆周不同位置的径向磁力的光谱分布Fig.5 Spectral distribution of radial magnetic force at different positions along the circumference

2.2.2 不同斜极角的径向磁力

在PMSM的电磁设计中，斜极转子的斜极角α是指电机工作时转子d轴与定子a相之间的磁轴角度，其二维截面如图6所示。转子在轴向上等距离地分段，并且每个分段式转子设计成具有不同的斜极角，这种结构布局类似于定子斜槽的效果，可以有效地削弱齿谐波并改善永磁同步电机的转矩波动。

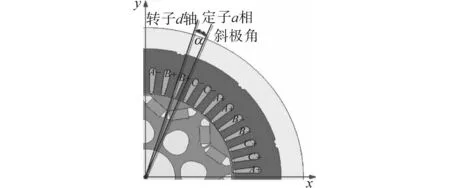
图6 斜极转子的二维横截面Fig.6 Two-dimensional cross section of inclined pole rotor

图7为径向力密度及具有不同斜极角的光谱波形图，结果表明斜极角越大径向力密度的幅值越大，并且径向磁密度峰值处的频率主要位于偶数倍基频附近。结合实验过程，分析原因如下：一是因为在研究不同斜极角的径向磁力中只考虑了径向分量的磁通密度在气隙中的效应，而对开槽、饱和以及其它寄生效应如偏心等均未考虑；二是研究过程中斜极角的范围选择过窄，导致无法在宽角度上显示出径向磁密度的变化情况。

图7 径向力密度及不同斜极角的光谱Fig.7 Radial force density and spectrum of different oblique polar angles

3 模态分析

在数值求解和分析中，根据几何尺寸和材料特性构造定子铁心的有限元。定子芯由硅钢片层压而成，在横截面和轴向上表现出不同的性质，因此定子芯的材料特性是三维正交的，并且与3个相互垂直平面对称的弹性特性是相同的。应力-应变的本构关系如下式所示：

式中：σ，τ，ε和γ分别为正应力、剪应力、法向应变和剪切应变的张量；T为结构温度；Tref为参考温度；A为热膨胀系数矩阵；G为刚度矩阵；E为杨氏模量；μ为剪切模量。

在有限元模型构建中，因为定子铁心和绕组之间的接触关系以节点耦合的方式建立，且定子铁心由硅钢片层压而绕组由铜线构成，因此无法对每根钢板和铜线进行建模，实际操作中只能以固体形式进行整体建模，如图8所示，其中定子铁心和绕组的材料参数经过对仿真模型的多次修改最终确定，如表1所示。

图8 定子铁心和绕组结构有限元模型Fig.8 Finite element model of stator core and winding structure

表1 定子铁心和绕组参数Tab.1 Stator core and winding parameters

当忽略温度对材料性能的影响时，刚度矩阵Gcore和Gwinding分别如下2式所示，单位GPa。

在锤击法模态测试中，加速度传感器附接到定子芯的外表面，使得基于定子结构的振动特性获得模态频率和模态形状。为了清楚地评估模态测试结果，在数值计算中将消除由绕组引起的局部模态，然后根据定子的空间模态形状实现前五阶测量结果，如表2所示。从表2可以看出，模态分析前五阶的平均相对误差为4.3%。图9为定子和整机的模态试验图，其中图9a为实验所用的电子铁心和绕组，图9b为实验电机组件。图10为电机组件的频率响应曲线，其中峰值频率对应于每个阶次电机组件的固有频率。

表2 模拟和测试结果比较Tab.2 Comparison of simulation and test results

图9 模态测试Fig.9 Modal test

图10 电机组件的频率响应曲线Fig.10 Frequency response curve of the motor assembly

4 噪声预测和测试验证

4.1 噪声预测

电机的电磁振动属于径向磁力作用下的强制电磁振动，因此当径向磁力的频率接近整个机器的固有频率时，将辐射出更大的噪声，且多物理场的耦合效应在一定程度上影响噪声的预测。因此实验中通过建立电磁-振动-噪声有限元模型（FEM）来计算PMSM的辐射噪声，其中所研究的电机极/槽为8/48，额定/峰值速度为3 980/9 000 r/min。图11为一阶模态频率附近的SPL分布，可以看出最大声压级为65.2 dB。

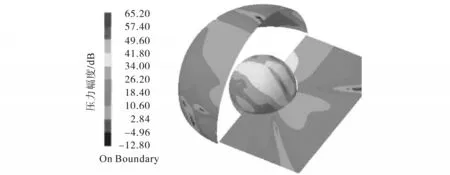
图11 一阶模态频率附近的声压分布Fig.11 The distribution of sound pressure near the first-order modal frequency

另外，在噪声预测实验中有斜极的FEM最大噪声幅度达到106 dB，无斜极的FEM最大噪声幅度达到85 dB。出现这种情况主要是在分段斜极FEM中，由永磁体确定的主磁通轴具有由绕组所确定的斜极角，然后将产生更多的谐波磁势。当电动机工作时，由永磁场和电枢场之间的相互作用引起的低阶径向磁力对电磁噪声产生一定的影响。

4.2 测试验证

该测试装置由测试电机、电机控制器、电池模拟器、变频柜、电机试验台、高压线束，信号线束和振动与噪声采集设备（包括功率分析仪以及主机监控系统）组成。测试设备图如图12所示。

图12 PMSM的测试设备图Fig.12 Test equipment diagram of PMSM

在测试过程中，麦克风安装在轴向端盖和电机径向侧附近，并连接数字采集设备，工作台测试如图13所示。

图13 PMSM的NVH台架测试Fig.13 NVH bench test of PMSM

图14为整机噪音测试结果。

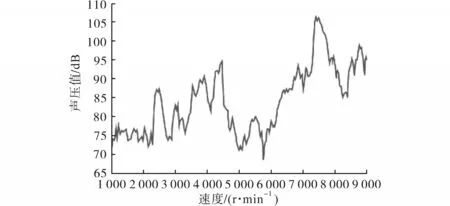
图14 整机条件下的噪音测试结果Fig.14 Noise test results under the whole machine condition

图14中，当测试电机转速为7 400 r/min时有最大SPL为106 dB。在额定转速为3 980 r/min时，SPL为87 dB，接近无分段斜极情况下模拟的SPL值（85 dB），二者之间存在的偏差较小。

造成预测结果与测量结果出现偏差的原因主要有：1）PMSM的结构FEM和接触关系等效地简化，并且不能完全表现出电动机的结构模式；2）在模拟计算过程中，电机在理想的空载状态下计算，而在测试过程中电机启动前需要克服一些摩擦力矩；3）电磁振动和噪声主要归因于该预测模型中的径向磁力，而实际的电机噪声不仅来自电磁噪声，还来自PMSM的转子不平衡和转矩脉动引起的机械噪声。

然而，通过比较计算和测试结果，本文中提出的多物理场仿真模型对于评估PMSM的电磁振动和噪声是有效的。

4.3 结果和讨论

在仿真和实验结果的基础上，为了减弱永磁同步电动机的电磁振动和噪声，可以从驱动电机的电磁设计中采取以下几个方面的措施：

1）电机结构的固有频率对电磁噪声有着重要的影响。为了降低电机的电磁噪声水平，在驱动电机的设计中，应尽可能远离PMSM的固有频率，以避免产生电磁共振。

2）转子斜极角对磁力幅值有明显的影响。在考虑电机转矩脉动的前提下，适当减小斜极角，这会削弱定子和转子磁场中产生的谐波磁势，降低低阶径向磁力的幅度，从而减弱电磁噪声。

3）谐波磁势会影响电磁振动和噪声。应合理设计定子和转子槽，优化绕组布置，降低定子谐波电位，使转子磁势接近正弦波，从而降低永磁同步电机的电磁振动噪声。

5 结论

在本研究中，建立了一个能够预测电磁噪声的多物理场仿真模型。基于验证的预测模型，提出了转子分段偏斜模型，并研究了电机噪声主要影响因素——径向磁力谱，最后，分析了斜极角对电磁噪声的影响，得出了以下结论。

1）通过建立多物理场仿真模型，理论上可以预测并合理地解释电机电磁噪声的分布特征。结果表明，无斜极的测试机器的SPL为87 dB，接近预测的85 dB。两种结果之间的差异主要是由于实验中忽略了电机启动时需要克服的摩擦力矩以及转矩波动和转子不平衡引起的机械噪音。

2）在频率范围内，电机在有、无转子分段斜极的情况下，电磁噪声的光谱变化是一致的，但是具有转子分段斜极的电机的SPL高于无转子分段斜极的电机的SPL。这是因为当由永磁体确定的主磁通轴与由绕组确定的主磁通轴成一角度时会产生更多的谐波磁势，并且由这些谐波磁势引起的低阶径向磁力将大大增加电机噪音。

3）不同斜极角下径向力密度的频谱分析表明，径向力密度峰值处的频率在沿圆周的不同位置处相似，峰值频率主要位于4 000 Hz以下。在不同的斜极角下径向力密度的光谱是不同的。斜极角越大，径向力密度越大，并且径向力密度峰值处的频率主要分布在偶数倍基频附近，针对这一现象后续将进一步进行研究以找到最佳斜极角。