实体动力学蒙特卡罗方法在核材料辐照损伤模拟中的应用

潘卓楠，杨章灿,*，周洪波，吕广宏

(1.华中科技大学，湖北 武汉 430074；2.北京航空航天大学，北京 100191)

核反应堆中严峻的运行条件对反应堆装置材料提出了巨大的挑战。材料暴露在高辐照水平的系统中，高能粒子的撞击会破坏材料原本完美的晶格，产生诸如位错、空洞、析出相等缺陷，而这些缺陷严重影响着材料的宏观性能[1-2]。辐照引起材料内部微结构演化在时间和空间上是个多尺度的过程，在实验上，很难实现原子空间尺度、微纳秒时间尺度上对实验的精准控制来进行缺陷演化机制的研究。而计算机模拟能够弥补实验上的不足，可用于解释微结构演化的机制，并且能够根据辐照条件对辐照效应提出预测。

辐照导致微结构演化的多尺度特性很难用单一的计算模型来研究，因此微结构演化模拟的研究通常使用多尺度模拟方法[3]。入射高能粒子与被辐照材料基体原子碰撞后产生初级撞出原子(PKA)，其能量分布可以通过粒子输运程序，如MCNP程序来计算。随后，PKA引发级联碰撞(<1 ps)产生大量的点缺陷，这个过程通常导致热峰的产生，极大升高级联区域的温度，可认为发生熔化。热峰区的原子不断将能量传递给周围的原子，由熔化状态快速(<10 ps)回到凝聚或淬火冷却阶段，最终建立热力学平衡态。冷却期间形成了稳定的点阵缺陷，包括点缺陷和缺陷团。以上过程通常称为初级辐照损伤，时间尺度约为10 ps，空间尺度约为数十纳米，可使用二体碰撞近似(BCA)方法进行缺陷数的快速估算，更为准确的计算通常使用分子动力学(MD)方法。

初级辐照损伤形成的稳定缺陷可发生热激发扩散，扩散到其他区域与级联内其他缺陷、材料中原有缺陷或其他级联区中的缺陷发生互相作用，最终形成空洞、气泡、位错等宏观缺陷。这一过程即微结构演化，时间和空间尺度均已达到实验观测的尺度，一般使用的模拟方法有动力学蒙特卡罗(KMC)、团簇动力学(CD)和相场方法(PF)。这些模拟方法通常需要MD或密度泛函理论(DFT)计算提供缺陷的热力学和动力学参数。

本文介绍的KMC方法是模拟受辐照材料微结构演化的有效工具，能够在保留缺陷空间关联性的前提下处理缺陷的扩散和缺陷之间的相互作用，并且具有足够大的时空尺度，使其模拟结果能够直接与实验值进行对比。KMC是一种基于马尔可夫过程的方法，在给定体系中各事件的发生速率之后，可以用于模拟体系随时间的演化。在材料模拟中，KMC方法不关注原子的具体运动轨迹，而将其粗粒化为体系组态跃迁的过程。组态的跃迁是无记忆性的，仅与跃迁的概率相关。KMC方法直接处理状态到状态的转换，因此相比于MD模拟方法，可以获得几个数量级的时间尺度增益。

根据对缺陷处理方式的差异，KMC方法可分为原子动力学蒙特卡罗(AKMC)、实体动力学蒙特卡罗(OKMC)和事件动力学蒙特卡罗(EKMC)。在微结构演化模拟中，OKMC方法对原子运动进行粗粒化，不考虑原子位置分布，将缺陷视作在晶格中移动的实体，用抽取事件发生的形式来模拟缺陷的演化，提高模拟尺度。本文将对OKMC算法和模型进行介绍，通过一些典型例子来介绍OKMC在材料辐照模拟方面的应用，从这些例子中分析OKMC方法的优越性和有待提高发展的方面。

1 OKMC的算法和模型介绍

通常，OKMC方法将缺陷及缺陷簇看作一个具有捕获半径的实体，实体具有与之关联的事件及事件可能发生的概率，通过事件的概率来抽取事件的发生，推进相应时间步长来模拟微结构演化。辐照导致微结构演化的多尺度特性示于图1。

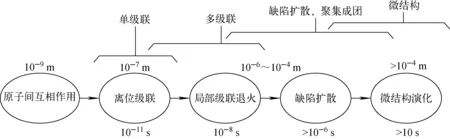
图1 辐照导致微结构演化的多尺度特性Fig.1 Multiscale characteristics of microstructure evolution under irradiation

1.1 KMC算法简介

不同于经典的基于Metropolis算法[4]的MC方法，在辐照领域应用的KMC方法多是无拒绝的MC方法，多基于RTA(剩余时间算法，也称为BKL算法)[5]。对于一个给定的系统，根据事件发生的速率所占权重来执行事件抽取，完成状态转化并计算间隔时间。在KMC中事件i发生的速率Γi可由下式计算：

(1)

式中：ΔEi为事件发生的势垒；kB为玻尔兹曼常数；T为温度；vi为尝试频率，可根据谐波过渡态理论得出：

(2)

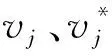
时间步长δt和平均时间步长Δt可由下式计算：

δt=-lnr/Γtot

(3)

Δt=1/Γtot

(4)

式中：Γtot为所有事件反应速率之和；r为0到1的随机数。

KMC将“原子运动轨迹”粗粒化为“体系组态跃迁”，忽略了若干次不会引发组态跃迁的原子振动，给出单位时间内体系发生跃迁的概率，从而推导出发生1次组态跃迁的时间。因此KMC的时间步长可以看作真实物理系统中体系穿越势垒发生组态变化所需要的若干次振动的总时间。

因此，KMC算法的基本步骤可总结如图2所示。

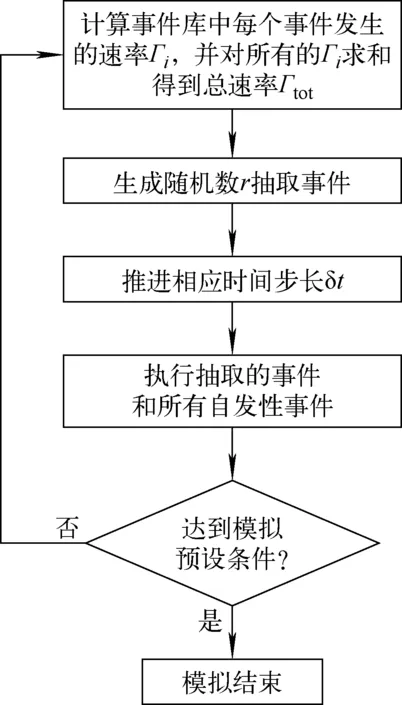
图2 KMC算法流程图Fig.2 Flowchart of KMC algorithm

1.2 OKMC模型

OKMC模型主要包括实体以及实体之间可能发生的反应，诸如自间隙原子、杂质原子、嬗变元素、空位以及它们形成的团簇、位错、空洞等缺陷均被当成实体。OKMC实时跟踪这些实体(缺陷)的位置。实体的特征包括它们的类型、尺寸、位置、方向、形状和捕获半径。OKMC方法可将实体处理成球形或其他任意形状[6-8]。另外，在OKMC方法中，晶界和表面被视作面吸收缺陷，能够吸收到达其表面的其他缺陷[6,9-10]。实体的捕获半径通常使用第一性原理进行计算[11]，当实体之间的距离小于实体的捕获半径之和时，实现实体之间的反应，如成团、复合或湮灭。

OKMC中的事件由用户自定义。通常，事件库中包含的事件如下。

1) 扩散(迁移)：即缺陷向近邻位置的移动。根据材料的不同、缺陷的不同，扩散会有不同的方向、不同的维度，这些扩散事件的发生由相应的速率控制。

2) 转向：一维或二维运动的缺陷改变当前扩散方向。

3) 成团：相同种缺陷或不同种缺陷之间的距离小于它们的捕获半径之和时，形成一个更大的缺陷团簇，如两个单空位(V)发生成团形成1个含有两个空位的空位团簇，即V1+V1→V2。

4) 复合：异种缺陷之间的合并。如1个三空位的团簇和1个单自间隙原子(SIA)发生复合之后，形成1个双空位团簇，即V3+SIA1→V2。

5) 解离：缺陷团簇释放出单个缺陷的过程。如1个三空位团簇释放出1个单空位的过程，V3→V2+V1。

6) 捕获：缺陷被一些特殊的杂质原子或位错等捕获。

7) 湮灭：指缺陷被自由表面、晶界或其他微结构吸收移除的过程。

8) 陷阱突变：金属中含有一些稀有气体元素时观察到的常见现象。如在聚变和裂变条件下，金属材料中含有氦时，氦原子被金属原子排斥，形成团簇。当团簇中氦原子的数量较多时，氦团簇会挤出1个或多个基质原子，产生1个或多个弗伦克尔对(Frenkel Pair)，甚至产生位错环。

9) 辐照事件：在OKMC中通过不断引入缺陷模拟辐照过程，可通过随机引入缺陷的方式实现，也可通过以一定速率引入缺陷级联的方式实现。引入速率可根据NRT模型[12]计算，即不同反冲能量T下的单个级联产生的离位次数vNRT为：

(5)

式中，ED为材料原子离位阈能。

其中缺陷的成团和复合属于自发事件，当缺陷之间的捕获半径之和小于缺陷之间的距离时，便会发生。而缺陷的扩散、转向、解离是由一系列的势垒和尝试频率来描述的，其中扩散事件发生的速率为：

(6)

式中：vd为扩散事件的尝试频率，金属中，单个点缺陷迁移的尝试频率约为金属的德拜频率；Ed为相应的扩散势垒，通常由第一性原理[11,13]和分子动力学计算[14]可得出。

转向事件发生的速率为：

(7)

式中：vt为转向事件的尝试频率；Et为相应的转向势垒。

解离事件发生的速率为：

(8)

式中：ve为解离事件的尝试频率；Eb为相应缺陷的结合能。

2 OKMC方法在材料辐照领域中应用的典型例子

OKMC方法在辐照模拟领域应用甚广，既可为更高尺度的模拟方法提供输入，也可在大尺度范围(空间尺度可达微米级别，时间尺度可达月、年)模拟材料的辐照效应。本节按照OKMC方法在不同尺度下的应用进行介绍。

2.1 计算缺陷阱吸收强度

OKMC方法可计算缺陷阱吸收强度，来为平均场速率理论这类更高尺度的模拟方法提供必要参数，因此获得可靠的缺陷阱吸收强度对于平均场速率理论的计算具有重大的意义。在速率理论中，缺陷阱吸收强度指可移动的缺陷被一些具有特定形状、大小、可充当陷阱的缺陷团簇、微结构吸收的速率[15-18]。缺陷阱吸收强度与缺陷的平均自由程的平方呈反比。它与缺陷的大小、形状和密度以及缺陷迁移的维度有关。基于扩散理论，Brailsford和Bullough推导了三维极限迁移下的球形缺陷[15]和晶界[16]的缺陷阱吸收强度理论值。Barashev等[19]推导了在一维极限迁移下缺陷的缺陷阱吸收强度理论值。Wiedersich[20]发表了关于位错线的缺陷阱吸收强度的研究结果，随后Nichols[21]对此进行了修正。在一维到三维的过渡迁移机制中，缺陷阱吸收强度的理论推导值可由Trinkaus和Heinisch等[22-25]提出的主曲线函数进行描述。

一般来说，在使用OKMC方法模拟计算缺陷阱吸收强度时，模拟盒子中1次仅放入1个可移动的缺陷，直到这个可移动缺陷被事先预置的吸收体捕获之后，再引入下一个缺陷并记录该缺陷跳跃的次数。经过足够多次的模拟之后，得到的缺陷阱吸收强度k2如下式所示：

(9)

式中：n为缺陷扩散的维度；d为缺陷跳跃1次的距离；〈N〉为缺陷的平均跳跃次数。

根据经验，要使获得的缺陷阱吸收强度的误差小于1%，至少需统计104次，要使误差小于0.1%，则需要统计106次以上[26]。在OKMC中，一维迁移的缺陷始终在一个方向上来回进行跳跃，三维迁移的缺陷在每跳跃一步之后，可以随机选择跳跃方向。OKMC处理一维到三维的过渡迁移机制主要有两种方法：一是在迁移固定的次数nd之后使缺陷改变跳跃方向；二是给缺陷分配转向能垒Er，让缺陷在每跳跃一步之后有一定的概率改变跳跃方向。

Jansson等[9]使用OKMC方法计算了位错和位错线的缺陷阱吸收强度，并且与理论值符合良好。Malerba等[27]则使用OKMC方法分别计算了球形吸收体、晶界对不同迁移维度的缺陷的缺陷阱吸收强度。一维和三维运动的情况下可直接与理论公式进行对比，混合一维/三维运动情况下，需与主曲线方程进行对比。对于球形吸收体和球形晶界，OKMC模拟计算得出的缺陷阱吸收强度均与理论值符合较好。

另外，有研究[22-23,27-28]表明：OKMC的仿真结果会高估大体积吸收体的缺陷阱吸收强度，而低估小体积吸收体的缺陷阱吸收强度；与大体积分数情况相比，在小体积分数下，周期性分布的位错线缺陷阱吸收强度与理论值吻合更好。针对这些偏差，Hou等[29]做了相关的研究，揭示了其间的差异起源，并且在理论上提出了修正。他们认为，低体积分数的情况下，造成偏差的主要原因是：OKMC模型中离散的扩散形式与实际连续扩散之间的差异；高体积分数的情况下，吸收体之间的相互重叠情况是造成差异的主要原因；另外，OKMC模型中位错线的周期性分布是导致一维迁移下出现锯齿状差异的原因。在考虑了这些差异并做出修正之后，模拟值与理论值之间得到了更好的吻合。Ahlgren等[26]对缺陷阱吸收强度的理论值推导进行了修正，并开发了名为“N-jumps”的蒙特卡罗方法：通过可移动缺陷与吸收体之间的最小距离来确定可能需要的跳跃次数，然后使用1次“大的跳跃”等效替代N次单独跳跃的效果，从而提升模拟速度。在吸收体的体积分数较低时，提升效果更为显著。

通过以上的研究可了解到，OKMC方法是模拟计算缺陷阱吸收强度的有效工具，并且与理论推导值有很好的吻合。但在某些吸收体体积分数下，OKMC方法的仿真结果与理论值总是存在一些偏差，这种偏差来源于OKMC模型的离散化处理与理论连续性假设之间不可避免的差异。因此，有效的处理方法是分析差异来源，并且基于现有的模型进行适当修正。OKMC方法缺陷阱吸收强度计算的精准度取决于对缺陷动力学模型细致的考量，因此需要MD或DFT提供更为准确的缺陷互相作用模型，以及缺陷的热力学和动力学参数。此外，在小吸收体体积分数和缺陷一维迁移条件下，缺陷被吸收前的平均自由程较长，导致OKMC模拟缓慢。如何有效地解决该问题，也是OKMC方法需要改善的方向之一。

2.2 级联内退火模拟

辐照产生的PKA与其他原子相互碰撞，导致材料内部原子发生离位和进一步的碰撞，形成一定的缺陷空间分布，这个过程称为位移级联。随着级联能量的耗散，产生的缺陷集中分布在初级损伤区域，这个过程通常在十几皮秒内完成。随后，初级损伤区域内的缺陷之间会发生进一步的复合、成团等相互作用，直到缺陷的空间、尺寸分布趋于稳定，这个过程称为级联内退火。级联内退火过程的持续时间通常为数纳秒到数十纳秒不等。位移级联经过级联内退火之后尚存的缺陷数目、大小和空间分布以及材料中的杂质会对辐照微结构演化产生影响[30]。因此，充分了解级联内退火的特征对级联插入式的OKMC辐照模拟具有重大意义。

Xu等[31]使用分子动力学模拟得到的初级辐照损伤数据库进行了bcc铁中的级联退火模拟，并进行了参数敏感度研究。得到的结果可作为平均场速率理论的源项。模拟主要结果如图3所示，其中自由的SIA分数表示经过级联之间的相互作用之后可脱离级联区域并且不再与级联内其他缺陷发生反应的SIA分数。可看出PKA能量越低，模拟结果的波动越大。这是由于低PKA能量下，级联中的缺陷数量较少，在统计上的波动更大。而在能量大于20 keV时，统计误差就较小了。从结果可看出，自由的SIA分数约为55%～70%，与PKA能量的关联度不高。参数敏感度分析涵盖了不同的PKA能量、不同的SIA运动机制、缺陷团簇解离情况、不同的捕获半径以及模拟盒子的大小。研究发现，SIA的运动机制对模拟结果的影响最大，当越多的SIA团簇以三维形式扩散时，逃离级联的SIA比例越低。另外，当所有的SIA团簇均以三维形式扩散时，复合效率最高。

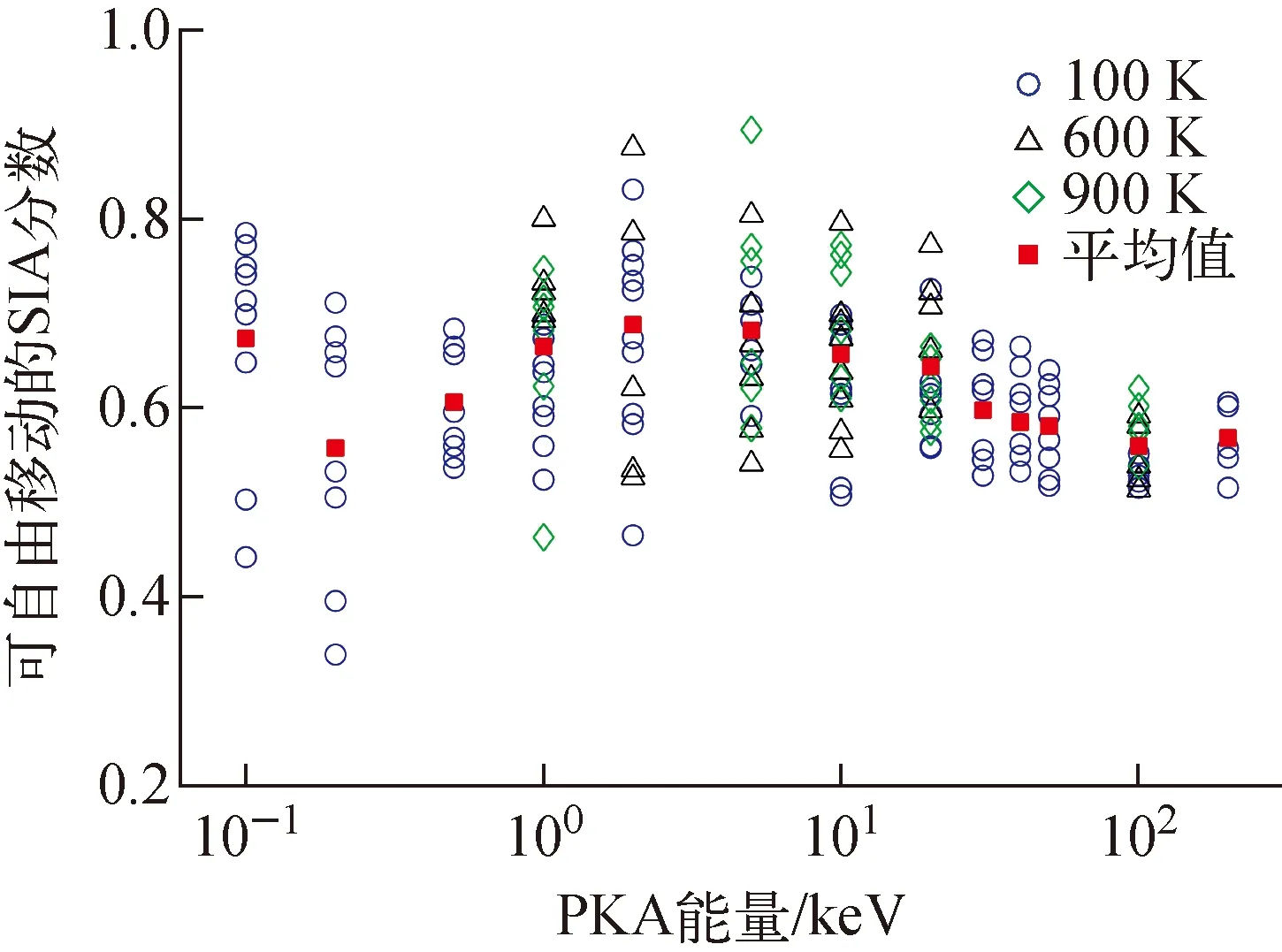
图3 bcc铁中不同PKA能量的级联退火模拟结果[31]Fig.3 Cascade annealing simulation results of different PKA energy in bcc iron[31]

Nandipati等[6,32]使用OKMC对钨的级联内退火进行了模拟，并且进行了点缺陷动力学参数敏感度的分析。同样以分子动力学模拟[33]结果作为输入，典型模拟结果如图4所示。级联退火过程可分为两个阶段：阶段1，SIA和空位之间的复合基本完成；阶段2，SIA逐渐扩散到吸收边界而从模拟盒子中移除，而空位基本保持不动，因此模拟盒子中SIA数量不断减少，而空位数量基本不变。同时，Nandipati等也进行了参数敏感度研究，发现级联内退火行为取决于缺陷的空间和尺寸分布，以及缺陷的相对迁移速率。具体来说：1) PKA能量会影响缺陷的尺寸分布和空间分布，进而影响复合效率。2) 复合效率随温度从300 K到1 025 K呈现增长的趋势，然后在2 050 K时下降，与温度的关系表现出倒U型数曲线，这说明退火行为的演化是温度和PKA能量共同作用的结果。3) 在金属钨中，由于SIA的迁移速率远大于空位，因此SIA的迁移和小SIA团簇的转向主导着级联内退火行为；SIA扩散的维度也存在影响，三维扩散下的退火效率高于一维扩散。

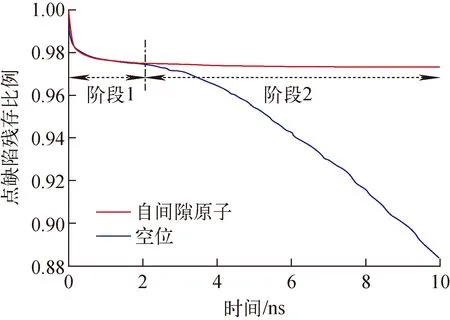
图4 钨中PKA能量为75 keV的级联在300 K的温度下退火10 ns点缺陷的数量变化[6]Fig.4 Change of number of point defects for cascades of PKA energy of 75 keV in tungsten annealed at temperature 300 K for 10 ns[6]

级联内退火模拟服务于相应条件下材料微结构演化模拟，模拟结果经处理也可作为平均场速率理论的关键输入。但由于单级联退火的时间通常很短，一些在单级联退火过程中不敏感的参数，在长期演化中仍可能会对模拟造成不可忽略的影响。因此，如何有效地将单级联退火的模拟结果应用到长时间演化模拟中，需进行进一步的研究。另外由于OKMC方法忽略了缺陷的原子尺度的细节，缺少了缺陷构型的信息，而不同构型缺陷的动力学参数往往也不相同。恰是由于OKMC方法在这方面的局限性，所以在模拟中不得不进行一些假设。

2.3 微结构演化模拟

级联碰撞产生的缺陷的空间分布和迁移率是不均匀的，这种不均匀性导致局部的缺陷之间发生相互作用，这种行为被称为空间关联效应[34]。空间关联效应的存在，会使缺陷的空间、尺寸分布变复杂，对长时间的微结构演化模拟产生很大的影响。不同于一般的平均场方法，OKMC方法可在考虑到空间关联性的前提下，模拟空间尺度为纳米到微米级别、时间尺度根据不用的应用场景可到小时、日，甚至月、年的微结构演化。模拟可得到材料内部缺陷的尺寸分布和空间分布，并且能够与实验结果进行对比验证。本节将通过反应堆压力容器钢的脆化机理研究、碳杂质对微结构演化的影响、空洞阵列的形成3例，对OKMC方法在模拟微结构演化上的应用进行介绍。

1) 反应堆压力容器钢的脆化机理研究

用于辐照实验和反应堆运行的材料很难做到100%的纯度，在辐照过程中也会有嬗变元素的生成，加之合金材料的广泛应用，在OKMC方法中如何处理多种元素成为了研究的热点，如反应堆压力容器钢的脆化机理研究[35-40]、氢元素和氦元素对钨微结构演化的影响[41-42]、碳杂质对空洞肿胀的影响[36,43-44]等。

目前对于异间隙原子(FIA)的处理主要分为显式引入和隐式引入两种方式。前者通过直接在模型引入原子，增加相应的FIA与点缺陷形成的络合物和相互作用；后者通过等效替代或引入缺陷阱吸收强度的方法来实现。

反应堆压力容器(RPV)作为核电站反应堆的重要组件，其安全性直接影响着反应堆的使用寿命。通常使用低合金贝氏体钢、铁素体钢作为RPV的结构材料。长时间暴露于强辐射下，RPV钢中会产生大量的点缺陷和小缺陷簇，而这些缺陷簇可能演变成空洞和位错环，进而使RPV在宏观上表现为屈服强度增加(硬化)、断裂韧性降低、韧脆转变温度(DBTT)增加(脆化)[45-50]。

RPV钢的脆化主要由于富锰(Mn)和富镍(Ni)团簇的形成[51-52]。OKMC方法由于具有大时间尺度的特性，足以模拟RPV钢的整个寿命周期，Chiapetto等[35,37-38,40]对此提出了Fe-C-MnNi合金模型，使用OKMC方法研究了溶质元素在辐照下对纳米级微结构演化的影响，通过修改缺陷迁移参数隐式地引入合金元素。模拟结果表明，与Fe-C相比，Fe-C-MnNi合金中大的空位团簇、SIA团簇和空洞的形成受到抑制。这些结果与正电子湮没谱(PAS)实验值一致[53]。此外，Mn浓度也会对微结构演化产生影响。Mn的浓度升高会导致SIA团簇增多，但在Mn的浓度高于1.2%之后，SIA团簇的数量不再明显受到Mn浓度变化的影响。另外，由于空位团簇的迁移率不随Mn浓度改变而变化，所以并未观察到空位团簇的明显变化。

Fe-C-MnNi的OKMC模拟可清楚地揭示RPV钢脆化的机制：点缺陷簇迁移率的降低，导致Fe-C和Fe-C-MnNi合金之间微结构演化发生显著差异。为更好地与实验结果进行比对，Chiapetto等[35]对这套模型和部分参数集进行了进一步的修正，然后针对两种不同的合金(Fe-C-MnNi合金和Ringhals RPV钢)进行了模拟，模拟结果与实验结果符合良好，如图5所示。此研究进一步证实了富MnNi团簇是由小间隙原子环形成的溶质富集产生的。

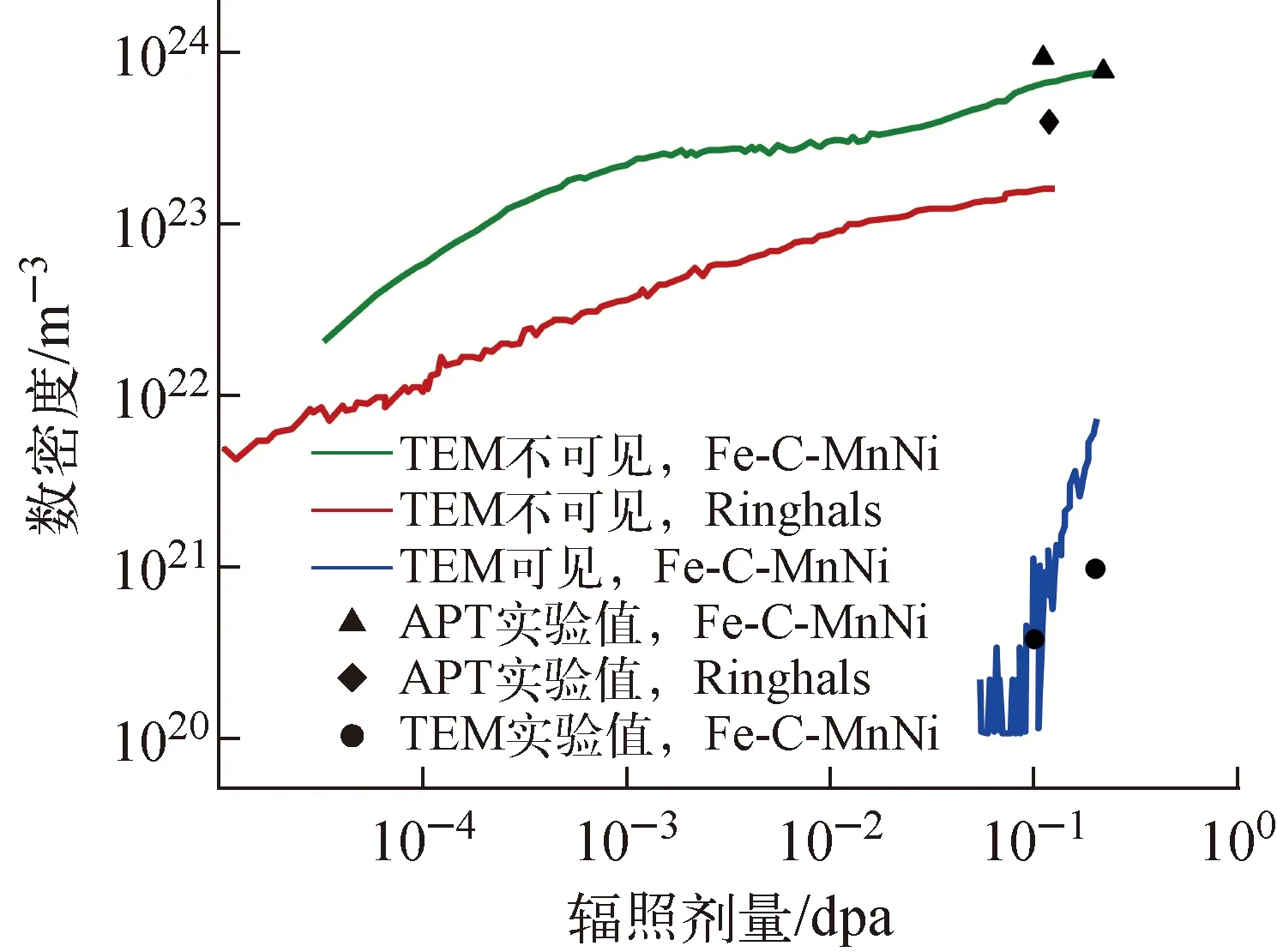
图5 Fe-C-MnNi合金和Ringhals RPV钢中SIA数密度随辐照剂量的变化趋势[35]Fig.5 Density of SIA in Fe-C-MnNi alloys and Ringhals RPV steels with irradiation dose[35]

2) C杂质对微结构演化的影响

C杂质广泛存在于各种金属中，无论是在RPV钢中，还是在其他金属材料，如选用为ITER偏滤器材料的金属钨[54]中，C杂质的存在均会对其机械性能造成影响[45,51]。

OKMC模型的隐式引入方法中，使用球形吸收体来表示等效替代C原子效应的陷阱元素。在α-Fe中，C原子易与空位结合形成CV、CV1、CV2、C2V等络合物，影响SIA和空位在基质中的迁移。相关的MD模拟发现CV、CV2和C2V络合物非常稳定，并且，CV络合物与1/2〈111〉SIA簇的结合能取决于与SIA簇的作用位置是边缘还是中心[55]。而在不同的退火温度下，络合物的形式也有不同[36]。在α-Fe中，Jansson等[36,44]使用隐式引入的方法来模拟C原子的影响。首先通过简单的预实验，显式引入C原子，确定CV络合物在不同温度下的主要构型，然后在不同的温度下确定不同尺寸的SIA团簇与C、CV络合物的结合能。使用陷阱元素等效替代C以及CV络合物之后，陷阱与点缺陷之间的捕获效应体现在缺陷团簇的动力学参数变化上。点缺陷一旦被陷阱捕获，便以结合能Eb来束缚。

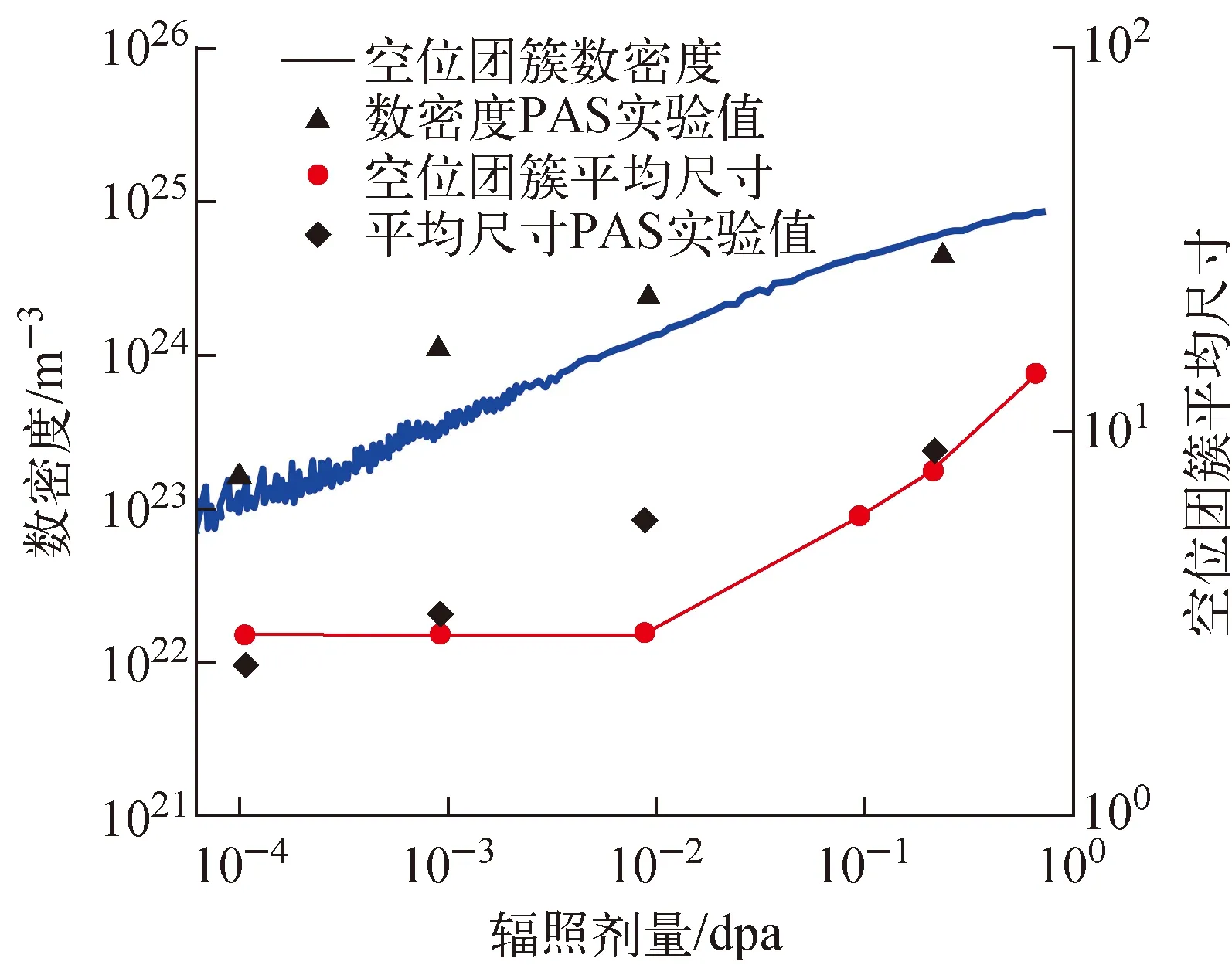
图6 空位团簇数密度和平均尺寸与辐照剂量的关系[44] Fig.6 Relationship between density and average size of vacancy clusters and irradiation dose[44]

图6为Jansson等模拟α-Fe中Fe-C的微结构演化的部分结果。模拟温度为343 K，采用级联插入的方式模拟辐照，缺陷级联来自于已有数据[56-61]，引入速率相当于7×10-7dpa/s。空位团簇的数密度随辐照剂量的上升而上升，与实验结果符合良好。同时，Jansson等还进行了等时退火模拟，起始温度为333 K，温度梯度为50 K，在一个温度下退火3 600 s。依据预实验的结果，改变不同温度下C源陷阱与SIA的结合能。总体上，模拟结果与实验值符合较好。

OKMC的灵活性可满足不同方式的隐式引入方法。Castin等[10]通过计算在不同浓度下C的缺陷阱吸收强度，然后将其转化为点缺陷与C源陷阱的作用概率，来表示C杂质引入的效果。并且，此研究还假设：随空位团簇的长大，C对空位团簇的捕获效应降低，即相应的结合能Eb降低。研究结果表明，C含量的变化对空洞形成的动力学过程有很大影响。因为C对空位的捕获导致了进入空洞的空位减少，使空洞平均直径减小，延缓了空洞的生长。另外，由于空位成团的减少，小空位簇的弥散程度升高，导致辐照引入的SIA易与之复合，使空洞数密度降低。

以上OKMC研究表明了杂质元素通过与点缺陷的作用来影响点缺陷团簇的演化，从而影响微结构的演化。但这些OKMC研究大都对模型进行了一些假设或简化处理，如假设SIA团簇与C的作用存在尺寸阈值，这个阈值决定了二者的作用类型是边缘弱作用还是中心强作用[44]。这种假设虽是根据理论研究结果和DFT模拟结果进行的简化处理，但其正确性尚有待验证，也需进行相关的敏感度研究予以支撑。

在使用OKMC方法处理溶质元素的影响时，显式地引入新的元素能够直接处理溶质元素在基体中的扩散，得到直观的、明确的团簇尺寸和空间分布。但实际上很难实现溶质原子与空位或SIA缺陷之间相互作用的精确建模，并且这样的处理给计算增加了负担。首先，根据KMC算法可知，显式地将它们包括在模型中，会大幅增加总反应速率Γtot，减小时间步长Δt，将不可避免地并显著增长KMC总模拟时间。其次，模型中的事件数量将呈现几何式的增长，变得难以管理。隐式引入方法使得模型变得更易处理，减轻了计算负担，但打破了溶质元素在基体中分布的不均匀性，不能利用OKMC处理空间关联性的优势，对模拟结果的影响程度尚有待研究。因此，在保留空间关联性的前提下，如何融合其他方法来提高OKMC模拟效率也是有价值的研究方向之一。

3) 空洞阵列模拟

空洞阵列是指受辐照材料在高温、高剂量辐照下形成的空洞有序排列的情况，空洞超晶格的构型通常与材料本身的晶格构型相同。1971年，Evans在钼离子辐照实验中[62]首次发现空洞阵列的形成。1972年，Sikka等发表了钨在中子辐照下形成空洞点阵的实验研究结果[63]。这项研究在EBR-Ⅱ反应堆中进行，于550 ℃照射至1×1022cm-2中子通量。他们分析得到了空洞超晶格参数，并且与金属Mo和Ta进行了比较。Loomis等在金属Nb及其合金中研究了空洞点阵的晶格参数随辐照条件的变化[64]。Tanno等[65]进行的钨中子辐照实验中，在750 ℃辐照至1.54 dpa时，也发现了空洞阵列的形成。

目前关于空洞阵列形成的主流观点是阴影效应[24]及其衍生理论。阴影效应认为，形成空洞阵列的核心点在于空位和SIA运动方式的不同。如在bcc金属钨中，空位的扩散一般认为是三维的，而可移动的SIA沿着密排方向一维迁移。恰是由于这种运动方式的差异使得空位在特定位置聚集、排列，最终形成空洞阵列。

OKMC模拟能够很好地体现SIA不同运动方式的差异，有效地处理空洞形核过程，并且能够给出空洞的尺寸、空间分布，很适合用于模拟空洞阵列的形成。图7示出了使用OKMC方法模拟空洞阵列的结果示意图。Heinisch等[24]使用OKMC方法针对空洞阵列的形成机理进行了研究。他们设计了1组对照模拟实验：预置空洞并按阵列排布、预置空洞随机分布。模拟盒子中仅入射SIA，发现空洞阵列的形成需要足够长的SIA一维运动路径，而SIA过于频繁的转向将不会形成空洞阵列。另1组对照模拟实验分别在3种方案下进行模拟：1) 预置14个按fcc结构排布的大空洞作为“种子”；2) 在模拟盒子中心预置1个大空洞作为“种子”；3) 无预置空洞作为“种子”。3种方案均预先随机放置了1 000个小空洞，在模拟盒子中持续入射空位和SIA来模拟辐照。以上3种方案均形成了空洞阵列，但方案1中形成的空洞阵列的晶格参数最大，并且在有“种子”的情况下，空洞会发生解离或移位到格点上。该研究侧重于探索在阴影效应的理论基础下，SIA的运动方式如何对空洞阵列形成稳定性造成影响。模拟中采用了许多假设，如入射的SIA和空位均视作尺寸为7的团簇、缺陷遍历模拟盒子4次便会被删除等，并且忽略了空洞的形核过程。这与现今许多OKMC模拟一致，并未采用真实的模型和参数，缺少与实验之间的对比来验证理论的正确性。

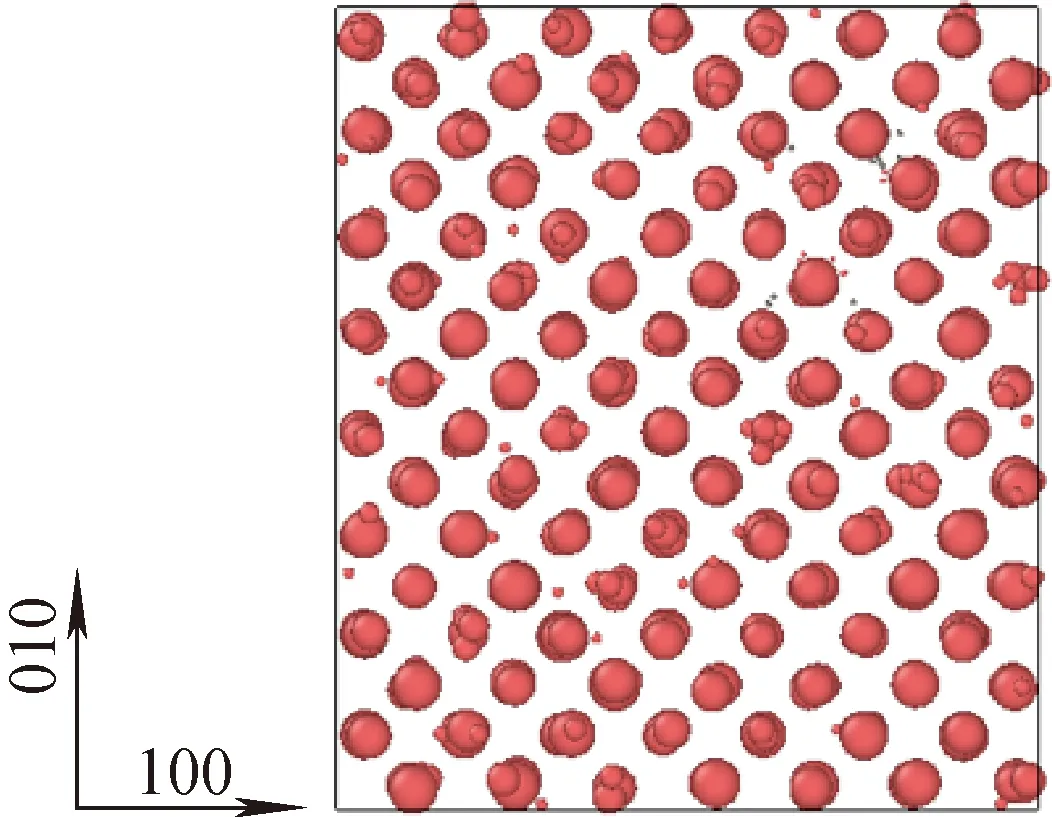
图7 OKMC方法模拟空洞阵列的形成Fig.7 Formation of void lattice simulated by OKMC method

因此，目前关于空洞阵列的OKMC模拟尚有较大的发展空间，特别是在模拟盒子形状和尺寸、边界条件的设置问题上。直接以真实的晶粒尺寸作为模拟盒子的尺寸，使用吸收性边界条件作为晶界是模拟多晶材料辐照最理想的设置，但这样会导致计算量剧增，不太现实。所以，周期性边界条件受到广泛应用。然而，OKMC模型在处理一维迁移的缺陷时，如果使用周期性边界条件，在缺陷穿越边界后人为地限定重新进入模拟盒子的位置，将不可避免地导致一维运动缺陷的迁移路径受到模拟盒子边长比例的影响。如果使用立方体的模拟盒子，会使一维运动的缺陷一直重复同一条路径，如图8a所示；如果使用非立方体的模拟盒子，如图8b、c所示，会使一维迁移的缺陷每次穿越边界之后的路径之间的间距与模拟盒子边长的最大公约数相等。这样会使得OKMC模拟中形成的空洞阵列的晶格参数将会被模拟盒子边长比所主导，甚至会掩盖辐照条件和缺陷动力学参数的影响。因此，如何合理地去除周期性边界条件对模拟一维运动的影响也是OKMC方法在材料辐照模拟领域的发展方向之一。

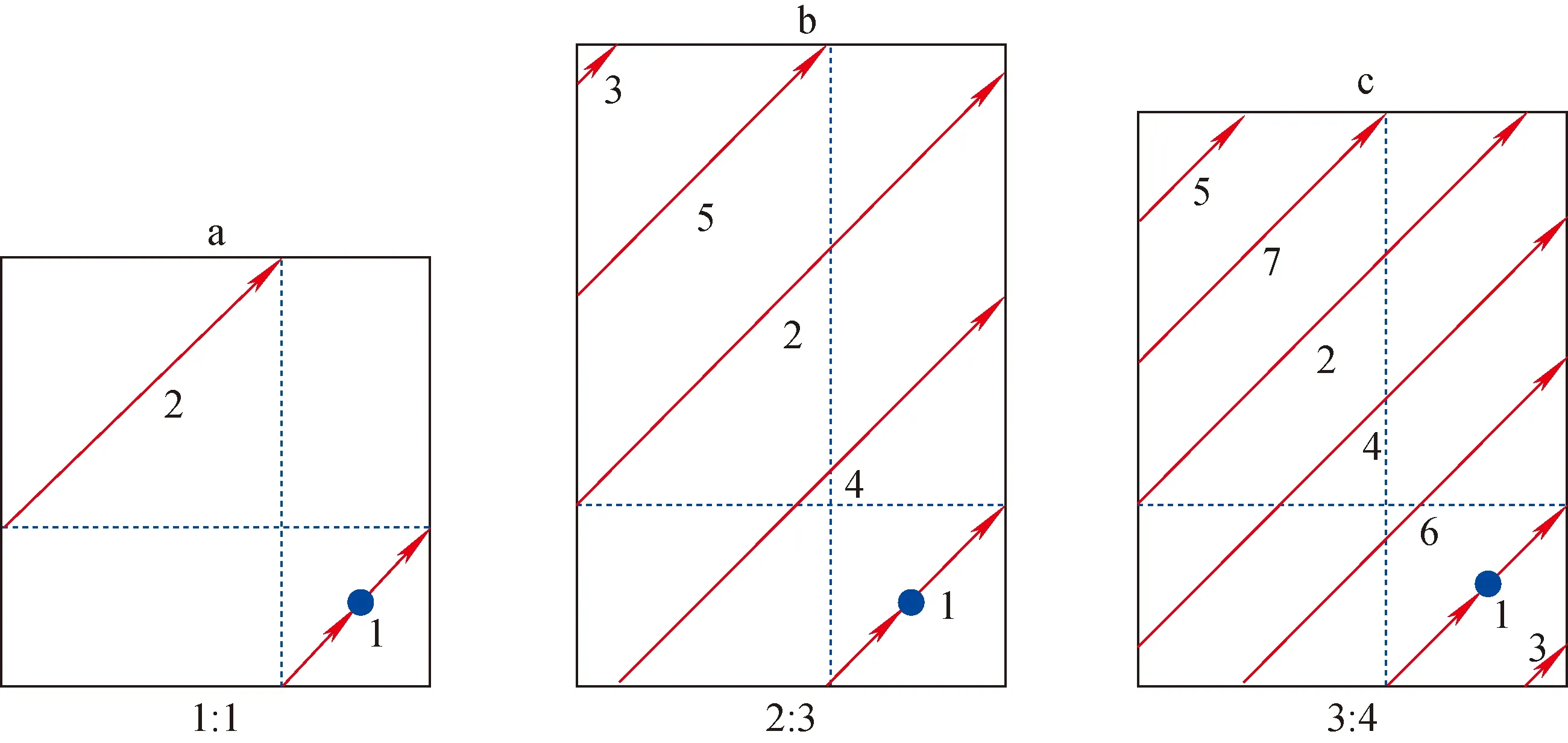
图8 不同边长比的情况下一维运动缺陷的轨迹Fig.8 Trajectory of one-dimensional motion defects in simulation boxes with different length-to-width ratios

3 总结与展望

本文对OKMC方法的原理和建模进行了介绍，通过例举一些现有研究，对OKMC方法在材料辐照领域的应用进行了详细介绍，并对OKMC方法的优势以及待发展和解决的问题进行了阐释。总的来说，OKMC方法具有MD、CD等方法所无法替代的特性和优势，主要体现在以下几点。

1) OKMC模型除具有足够的时空尺度之外，还具备捕获缺陷空间关联性的能力，而这些空间关联性极有可能是影响受辐照材料微结构演化的关键因素。

2) OKMC模拟能够给出可与实验进行直接对比的缺陷尺寸、空间分布等信息，并且现有的研究表明，OKMC模拟结果能够与实验值符合较好。

3) OKMC可用于确定平均场理论模型中的源项或输入项。

4) OKMC模型灵活，可建立缺陷参数与辐照效应之间的桥梁，很适合用于研究参数、假设对损伤退火和损伤累积的影响。

但OKMC仍存在不足。首先，由于OKMC方法不具备预知性，其误差主要来源于事件库和速率的不完整性，其次是低尺度输入的不确定性以及模型的统计误差。在真实的系统中，事件发生的速率是会随着时间变化的，并且还与系统的状态相关，而在OKMC中该速率与时间和状态无关。另外，OKMC中还假设各事件之间是独立的，然而在真实系统中，它们可能是相关的，这也是误差的来源之一。但完备的事件库往往不易获得，尤其是当所研究的体系性质复杂并且涉及多种组元或复杂的晶体结构时。

因此，为满足模拟需求，需对模型进行必要的简化，在准确性与效率中寻找平衡。在这种情况下对缺陷动力学模型进行合理假设，并且开展相应的敏感性分析是很有必要的。如Nandipati等[32]展开的敏感性分析表明了级联的退火效率主要受SIA迁移的影响，其中小SIA团簇的转向和迁移显著影响着SIA与空位的复合。因此，在建模过程中对于SIA的迁移和转向需要详细刻画，增加模拟的准确性；而对于其他的事件，可做一些简化，提高模拟的效率。此外，也可通过与一些简单实验进行对比，反推出模型中刻画不准确的参数和事件，调整相应的参数值和事件库。通过反复迭代进行对比调整，校正事件库和参数，增强OKMC方法在复杂条件下的模拟准确性。

即时动力学蒙特卡罗(On-the-fly KMC)算法[66-69]可克服事件库完备性的问题，即在执行KMC计算之前无需给出可能的事件及其发生速率，而是在算法步骤执行的同时确定可能的事件并计算其速率。这种方法在模拟合金中缺陷的演化尤其有效。因为合金中的一些特定的反应速率，特别是缺陷的扩散速率，取决于局部环境。但这种算法在OKMC方法中难以实现，通常是在AKMC方法中进行应用。因为实时确定可能的事件并计算其速率需知体系中所有原子的位置，以及它们之间的互相作用势这些信息，但OKMC方法中所有缺陷均被视为实体，丢失了这些原子尺度的信息。因此，未来的研究可考虑将OKMC和具备即时算法的AKMC结合，通过AKMC方法来实时更新关键的参数值和可能发生的事件，从而达到完备OKMC的事件库、提高OKMC模拟准确性的目的。

另外，由于OKMC中时间步长与总速率呈反比，因此在高温和高剂量率的条件下，OKMC方法的计算步骤量将会异常庞大，所能模拟的总辐照剂量将很小，不能满足与实验对照的需求。因此，这种情况下进行OKMC算法的并行化就十分有必要了[70-71]。但在处理一些高度不均匀的系统或系统内不同缺陷的迁移速率相差甚大的情况时，并行算法的性能将会严重受限。

综上所述，未来OKMC方法在辐照材料模拟领域应用需克服的挑战主要包括：

1) 解决算法的并行化的难题，显著提高OKMC方法的模拟效率；

2) 完善OKMC模型以处理多组分材料系统，包括不断发生嬗变的系统；

3) 与不同时间尺度、空间尺度的方法进行结合，构建材料辐照模拟的完整平台。