聚变堆中第一壁材料钨的紧束缚理论研究

叶小彬，何志海，潘必才,,*

(1.中国科学技术大学 合肥微尺度物质科学国家研究中心，安徽 合肥 230026；2.中国科学技术大学 物理系，安徽 合肥 230026)

聚变堆的安全可靠运行依赖较多因素，其中，面向等离子体的第一壁材料的稳定性是关键因素之一[1]。当聚变堆在正常运行时，第一壁材料承受着高能粒子的辐照和高热流密度的冲击[2-3]。在如此极端的环境中，面向等离子体的第一壁材料的结构会发生急剧的变化，从而强烈影响材料的热力学性质和微结构。现已采用实验和理论模拟对第一壁材料的微结构和热力学性能进行了广泛的研究[4-7]。

由固体物理可知，当材料的电子结构发生变化时，材料的结构和性质也会发生相应改变。因此，在物理上，为深入研究和理解材料的结构与物理性质的关联，需密切关注材料的电子结构。在核聚变堆中服役的材料身处极端复杂的环境，这些环境因素会强烈调制材料的电子结构。首先，聚变堆在正常运行的情况下，聚变堆中等离子体芯部的温度约为100 000 000 K。根据黑体辐射理论中的维恩位移定律，高温等离子体会源源不断地向其周围的第一壁材料钨(W)辐射以X射线为主体的高能光子。这些高能光子入射到材料，与材料中的原子作用，激发甚至电离原子中内壳层的部分电子。于是，第一壁材料W中有大量的电子处于激发态。其次，从等离子体芯部会溢出大量的高能粒子。这些粒子既有带电的离子也有电中性的中子。带电的离子虽受削刮层的控制，释放出来后的能量被减弱了，但仍有较高的动能，轰击第一壁材料后，将部分动能传递给被碰撞的W原子。这些获得较高动能的W原子发生高速位移。在高速位移时，W原子核外的外层电子因受原子核较弱的吸引作用而脱离W原子，因而此时高速位移的W原子其实就是高速位移的W离子。高速位移的离子通过库仑作用，诱导其周围的W原子中的部分电子被激发。处于激发态的电子是不稳定的，通常会经历一个特征时间后发生退激发。退激发有多种途径，如电子从高能级跃迁到低能级，释放出光子；或电子将部分能量传递给晶格，从高能态转变成低能态，这是一个无辐射的跃迁过程。无辐射跃迁包含着电子与声子的耦合和非热行为。其中，非热行为是指通过改变电子态使离子间的受力发生改变，从而改变材料的结构。在非热过程中，激发的电子将部分能量通过量子力学力做功传递给了晶格。在W中，无辐射跃迁是最主要的电子退激发的方式。

已有实验对聚变堆中的第一壁材料W受辐照后的微结构等物理问题进行了研究[8-10]。现有的大量实验数据来自于对辐照后的第一壁材料的探测，此时，材料不处于辐照的环境，所获得的数据包含着辐照后遗留的效果，不能真实反映辐照时对材料产生的实时效应。理论上也有许多的研究工作探究粒子辐照对W的微结构和热力学性能的影响[11-13]。在大量的关于核材料的理论模拟中，已有的主体的理论研究工作均在经验分子动力学和经典蒙特卡罗的构架中开展，缺少对电子激发效应的考虑。为在理论模拟中考虑电子激发效应，提出了双温度模型的理论模拟方案[14-16]和含时的紧束缚动力学方法[17]，但前者未考虑真实的量子态，后者采用单s态的紧束缚动力学研究离子辐照中的电子阻止本领，获得了较好的结果，但无法研究辐照时处于电子激发态下材料的结构演化规律，也不能计算材料的其他物理性质。

本文发展W体系的紧束缚势模型，在该势模型中，离子间的相互作用包含量子力学力，同时引入描述电子在不同激发态分布的电子熵。将紧束缚势模型与分子动力学结合，对处于不同激发态下材料的微结构演化进行研究。

1 理论研究方法

1.1 紧束缚势模型中的电子态

对于处于定态的体系，可通过求解其单粒子能量本征方程(式(1))获得其电子结构。

Hψk(r)=εkψk(r)

(1)

式中：H为体系的哈密顿算符；k为布里渊区的波矢；εk为体系的能量本征值；ψk(r)为相应的本征波函数。当体系的原子轨道波函数在空间上比较定域时，体系的本征波函数可在原子轨道波函数组合成布洛赫和函数为基的表象中展开：

(2)

式中：Ri为体系中第i个晶格矢量；φα(r-Ri)为体系中位于第i个晶格中位置矢量为r的原子的α轨道波函数；Ci,α为对应的展开系数。将式(2)代入式(1)，可获得体系的哈密顿矩阵元：

(3)

(4)

由式(3)和(4)可知，对一个体系的哈密顿矩阵的构造转化为对hjβ,iα的求解。式(3)包含同一个原子内部的库仑积分项hiα,iα和不同原子间的跳跃积分项。其中，hiα,iα可近似地等于相应的原子轨道能级。跳跃积分项中包含多中心积分，因而hjβ,iα的计算量很大。为简便计算，采用Slater和Koster提出的双中心近似[18]替代hjβ,iα中的多中心积分。

在Slater和Koster的双中心近似下，定义一些不同类型的键积分，如对1个只包含s、p原子轨道的体系中2个成键的原子i和j，它们之间存在着以下4种类型的键积分：

(5)

采用Slater和Koster定义的键积分可表达出上述的积分项，具体表达式可参考文献[18]。

为快速求解大规模复杂体系，进一步用经验公式表达上述键积分，从而避开大量复杂的积分运算。在构造的W体系的紧束缚势中，采用下列的经验公式表达键积分[19]：

(6)

Rij=rij(1+δ1Δ+δ2Δ2+δ3Δ3)

(7)

(8)

(9)

(10)

式(6)中的ll′m为键积分的类型，l、l′=s、p或d，m=σ、π或δ。为增强紧束缚势模型的可传递性，还考虑了环境原子的影响。环境原子对键积分的影响体现在式(9)中环境原子k对原子i和j之间的有效距离Rij(有效键长)上(式(7)，其中rij为原子i与j之间的距离)，环境原子k的构型决定了Rij的取值。在式(6)～(9)中，α1、α2、α3、α4、δ1、δ2、δ3、β1和β2是需通过拟合过程确定的参数。式(10)为键积分的截断函数，即键积分函数在原子之间的有效距离超过rcut后，会快速衰减至0。文献[19]给出了W体系的紧束缚势模型的具体参数。

1.2 紧束缚势模型中的总能

在紧束缚近似下，体系的总能Etot为：

Etot=Eband+Erep

(11)

(12)

式中：Eband为带结构能；εl和nl分别为体系中第l能量本征态对应的本征值和电子占据数，εl可通过求解本征值方程得到；fl为Fermi-Dirac分布函数；Erep为体系的总排斥能，可表达为原子间的排斥相互作用能，写成原子间对势的求和：

(13)

为增强紧束缚势模型的可传递性，采用一种多项式表述的方案，即：

(14)

F(x)=C0+C1x+C2x2+C3x3+C4x4

(15)

为减小计算量，紧束缚势模型通常采用最小基近似。因此在选取原子轨道基组时，只考虑价电子轨道以及最低的空轨道。对于W体系，选取5d、6s以及6p轨道作为原子轨道基组。

此外，还需要构造体现原子间排斥作用的两体排斥势，即式(14)中的φ(rij)。为了方便，丁文艺等选取与键积分表达式类似的经验公式作为两体排斥势的表达式，不同之处在于二者的参数不同，具体参数可参考文献[19]。

本文所使用的W紧束缚势模型已被用于研究完美W晶体的晶格振动谱、弹性常数、W中的点缺陷(自间隙原子、单原子空位)形成能和晶格熔化的熔点[19]、W在有限温度下的电导率和热导率[20-21]。这些研究结果与相关的实验结果和第一性原理计算的结果一致。

1.3 电子熵

量子力学的微扰论认为，一个处于定态的微观体系受突发微扰时，体系的定态不改变。高能光子和高能粒子作用到第一壁材料W时导致材料中的部分电子突然变成了激发态电子，而部分激发态电子通过非热效应将部分能量传递给晶格也可看成是体系的突发行为。因此，在研究这类突发行为时，可使用体系的定态方程求解，但同时要加入由于部分电子被激发而引起的电子熵对能量的贡献。

体系中的电子在能量空间中的分布遵从Fermi-Dirac统计分布。当体系中的一群电子处于不同的激发态时，其电子熵为：

(16)

式中，fi为Fermi-Dirac分布函数。于是，体系的自由能为：

(17)

1.4 紧束缚分子动力学

为在有限温度下对体系的原子结构的演化进行模拟，将紧束缚势模型与分子动力学结合。在紧束缚分子动力学(TBMD)中，体系的自由能对原子的位置坐标求偏导数：

(18)

即可获得该原子在各坐标方向上所受到的力。将原子所受到的力代入牛顿第二运动定律，采用差分方程求解[22]，可获得原子在受力时的空间位置随时间的演化。

对式(18)进行展开：

(19)

式中：rl为原子l的位置矢量；-∂Erep/∂rl为排斥能贡献的力；-∂Eband/∂rl为带结构能贡献的力，又称为Hellmann-Feynman力，其具体的表达式为：

(20)

式中，|ψk〉为电子的能量本征矢量，可表述成体系的原子轨道波函数的线性组合。

在分子动力学模拟过程中，每一时刻体系全部的N个粒子运动的速度为{vi(i=1,N)}，采用约束条件：

(21)

便能控制体系温度为Tion(Tion为体系的离子温度，不是电子温度Tel，当体系处于平衡态时，其离子温度与电子温度才会相等)时的演化。

由于TBMD中力的表达式包含量子力学力，因此较经验势，紧束缚势在描述原子间相互作用时包含经验势所缺失的内容。

2 结果与讨论

2.1 微结构中的电子温度效应

首先计算在有限温度的热力学平衡态下W晶体的晶格变化。由于体系处于热力学平衡状态，故体系中的晶格温度与电子温度相同，所以在计算中，Tion=Tel。图1a中的蓝色曲线示出了当体系的温度从500 K变化到3 500 K过程中W晶体的晶格膨胀率。计算的晶格变化率随温度的变化关系与实验结果几乎一致。为揭示晶格温度和电子温度在晶格膨胀中的效果，在计算中还分别考虑了Tion=0 K和Tel=0 K的情况。当Tel=0 K时，体系的晶格温度从500 K逐渐升高到3 500 K，此时，晶格的膨胀率均系统地低于Tion=Tel的情形，如图1a中绿色曲线所示。而当Tion=0 K时，如图1b所示，Tel从0 K升高到20 000 K时，体系的晶格常数也随Tel的增大而单调增大，且本文中基于紧束缚理论的计算结果与基于密度泛函理论的计算结果十分吻合。特别是当Tel大于5 000 K后，晶格快速膨胀。计算结果表明：在中等温度(～5 000 K)以下，W晶体的晶格膨胀主要由晶格温度驱动，但在温度较高时，电子温度导致的晶格膨胀效应不可被忽略。特别是当电子温度很高(>10 000 K)时，即便晶格温度不高，电子温度也会导致很大程度的晶格膨胀。电子温度导致的晶格膨胀是激发态电子的非热效应的一种宏观表现。激发态电子的非热效应是很抽象的复杂效应，建议采用实时原位测量材料在辐照下的晶格变化来检验上述物理效应。

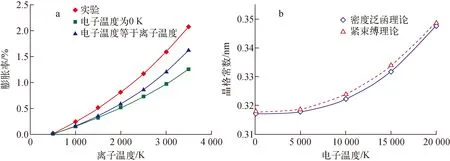
a——体系的温度500～3 500 K过程中W的晶格膨胀率；b——Tion=0 K下W的晶格常数随体系电子温度的变化图1 W体系的晶格变化Fig.1 Lattice change in W system

第一壁材料W拥有很大的表面。通常，W表面及其附近区域的原子受到的势场与W块体中原子受到的势场不同。采用由28个原子层构成的薄层模型模拟W的表面区域，薄层的表面取向为[001]方向，研究当表面附近区域承受高能光子辐照时其电子的非热效果。计算中，选取Tion=1 000 K和Tel=20 000 K进行TBMD模拟，并观察在模拟过程中一些不同时刻的薄层结构，如图2所示。

图2 W体系的结构演化Fig.2 Structural evolution of W system

显然，随着电子温度的加入，薄层迅速膨胀。当TBMD的模拟时间达2.6 ps时，薄层的中间区域开始呈现无序化。随着模拟时间的增长，这种无序化的程度加重，并快速转变成非晶的无序结构。同时，在无序结构的区域中出现了微孔。这些微孔的形状和尺度均随时间演化。这种结构的演化现象与飞秒激光辐照W材料时所呈现的现象非常类似[23]。值得注意的是，在结构演化过程中，靠近表面层的原子结构未呈现强烈的无序化特征，而是几乎保持原有的晶体结构特征。这与薄层中心区域的结构演化规律大相径庭。

图3 W的最近邻原子间相互作用力随电子温度的变化Fig.3 Interaction force among the nearest-neighbor atoms varies with electronic temperature

为理解上述的结构演化规律，分析体系在结构演化过程中原子所受到的力。如前所述，在紧束缚势模型中，体系中每个原子受到的力由电子结构引起的吸引力和原子间的排斥力构成。图3示出了W的最近邻原子间相互作用力的大小随体系电子温度的变化关系。可看到，当体系的电子温度为20 000 K时，所有原子受到的吸引力均大幅度减小，而电子处于激发态时，激发态电子对原子间的排斥势无直接影响。虽然如此，由于原子间的吸引力减小了，原子间的间距就会增大，这也相应地减小了原子间的排斥力。于是，从整体上看，当体系处于电子的高激发态时，体系的晶格大幅度膨胀。这种晶格膨胀是由激发态电子驱动的非热效应所导致。

随着分子动力学模拟时间的增长，薄膜上下表面原子层的原子通过驰豫缓慢释放应力。当原子层接近薄层的中心区域，这些原子层上非热效应导致的力必须通过与邻近原子层的作用释放，薄膜中间区域中的原子受到的非热力不易快速释放。再加上在晶格温度驱动下原子的无规运动，使得薄膜中间区域的原子表现出从有序结构向非晶无序结构的演化，并且中间部位的原子受到的非热应力通过其周围原子的有效驰豫减小，进而出现了孔洞。模拟时间足够长后，应力均被释放，部分孔洞逐渐被复合。

2.2 W表面的预熔化

通常，固体材料的表面熔化行为与块体熔化的行为不同。在表面的原子层，由于其中原子所处势场的特殊性，这类原子层熔化所对应的熔点要低于块体中的熔点，即表面预熔化现象。为研究W表面的预熔化，选择图4a所示的具有(110)表面结构的模型。在这个结构模型中，原子层的厚度约为3 nm，它由3个部分构成：底部按体相结构被固定的3个原子层，中间作为缓冲区的3个原子层和上面用于模拟表面的8个原子层。TBMD模拟中的控温条件均施加到用于模拟表面的8个原子层的区域。在各温度下各双层的均方键长涨落δ为：

(22)

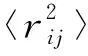
丁文艺等[19]在只考虑晶格温度效应而忽略电子温度效应时研究W的表面融化行为，发现原子层越靠近表面，局部的熔点变得越低。换言之，第一壁材料W的表面会表现出低于块体的熔点。在本文中，考虑电子温度效应，即Tion=Tel。其中，温度从1 000 K逐渐增大到3 500 K，如图4b所示。显然，考虑了电子温度后，W表面的熔点相对于未考虑电子温度时的熔点有所降低。特别是表面上的双原子层的熔点仅约3 000 K，低于未考虑电子温度时的3 500 K[19]。因此，当体系处于电子激发态时，表面的熔化温度也会下降。这种表面预熔化现象对于评估在聚变堆中服役的第一壁材料W的热力学性能十分重要。

a——分子动力学设置；b——Tion=Tel时不同深度的表面双原子层的均方键长涨落随温度的变化图4 W表面的分子动力学模拟Fig.4 Molecular dynamics simulation of W surface

3 结论

本文介绍了W体系的紧束缚势模型。将紧束缚势模型与分子动力学结合，研究W材料的微结构演化与热力学性质的电子温度效应。研究发现第一壁材料W表面的熔点低于块体的熔点，也低于未考虑电子温度时W表面的熔点。对W材料在非平衡条件(电子温度远高于离子温度)下的微结构演化进行研究，发现W的金属键随体系电子温度的升高逐渐变弱，导致W晶格的剧烈热膨胀。此外，当体系瞬间处于足够高的电子温度下，剧烈的热膨胀将导致体系在较低的离子温度下(远低于熔点)出现内部熔化而表面区域不熔化的反常现象。需强调，由于材料在聚变堆中受到粒子辐照时，被辐照的区域是局部和随机的，并非同时均匀发生在全部的壁材料上。因此，材料中那些被强烈辐照的局部区域才可能表现出上述预测的现象。

感谢中国科学技术大学超级计算中心提供的计算支持。