跨临界水湍流黏性底层数值模拟与分析

王 超， 陈 灿， 李鸿源， 徐 鸿

(华北电力大学 能源动力与机械工程学院，北京 102206)

超临界水在超临界水火力发电[1-2]、核能发电[3-4]、超临界水反应器氧化[5-6]和气化[7-8]等领域具有较高的应用价值，但腐蚀产物颗粒沉积带来的安全和经济问题越来越明显，包括传热阻力[9]和流动阻力[10]增加、发生堵管[11]和汽轮机磨蚀[12]等。

当水从亚临界状态被加热到超临界状态时，跨临界区水的物性参数变化很大，会导致传热恶化和流量波动，同时水工质在发电系统应用过程中往往会携带给水系统腐蚀产生的铁离子，并以颗粒的形式通过传质过程沉积在管道壁面[13]。因此，跨临界区的流场参数不仅影响传热，还会影响流体中腐蚀产物颗粒的传质。颗粒在近壁面的质量传递过程中，黏性底层反向升力能有效降低颗粒向壁面的扩散速率。反向升力的大小和作用距离分别由黏性底层的速度梯度和边界层厚度决定。因此，水跨临界流动的边界层变化对腐蚀产物颗粒的传质评估至关重要。

近年来，研究人员对跨临界区的传热和水的流量波动开展了相关实验和数值模拟[2,14]研究。为获得跨临界水流动的边界层特征，笔者采用SSTk-ω湍流模型[15]对直管中跨临界水流动进行数值模拟，研究跨临界区边界层厚度和速度梯度的变化特征，分析沉积层变化对颗粒近壁面传质的影响规律，为提高超临界水的工业应用安全性提供参考依据。

1 数学模型

选用(SST)k-ω湍流模型来描述连续相跨临界水的流动。流动计算中质量方程、动量方程和能量守恒方程分别如下：

(1)

(2)

(3)

2 几何模型及参数设置

2.1 几何模型

由于圆管为轴对称结构，借助Fluent软件二维求解器中的axisymmetric边界条件将其简化为二维对称结构。忽略流体的周向运动，采用二维模型可以减少计算的网格数目，从而减小运算量。为了提高近壁面流动模拟的准确性，对近壁面网格进行加密处理，如图1所示。

图1 几何结构与网格划分

对湍流充分发展区进行分析时，需计算入口段长度L*。

(4)

式中：d为管径，m；Re为雷诺数；G为质量流速，kg/(m2·s)；μ为工质黏度，Pa·s。

2.2 网格独立性验证

采用无量纲数y+来确定径向第1个网格节点与管壁之间的距离。

(5)

式中：uτ为壁面摩擦速度，m/s；y为壁面垂直距离，m。

一般要求近壁面第1层网格中心在紊流黏性底层以内，且y+约为1。在压力为25 MPa、热流密度q为600 kW/m2、质量流速G为1 000 kg/(m2·s)的条件下对网格独立性进行验证，结果如图2所示。由图2可知，在y+<1的情况下继续减小y+，壁温Tw几乎没有差别，因此取y+=0.8。

图2 网格独立性验证

2.3 边界条件

考虑到黏性耗散效应和近壁面处低雷诺数的影响，分别选择Viscous Heating和Low-Re Corrections条件。超临界水的物性参数调用REFPROP 9.0数据，利用线性插值方法定义流体性质。采用Stationary Wall & No Slip条件，考虑重力的影响，设置重力加速度的方向为竖直向下。压力-速度耦合求解器选用SIMPLEC算法，控制方程均采用二阶迎风格式。连续性方程、动量方程、湍动能和比耗散率方程的收敛残差设为10-5，能量方程的收敛残差设为10-6。

流体的计算压力为25 MPa，管径为8 mm，管总长为3 m。在数值模拟中设置的其他对比条件见表1。

表1 在数值模拟中设置的对比条件

3 结果分析

3.1 区域划分

图3给出了压力为25 MPa时流体密度ρ、比定压热容cp、动力黏度ν和体积膨胀系数E随温度的变化率。由图3可知，随着温度的升高，cp明显呈先增大后减小的趋势，在385 ℃时达到峰值，该温度点称为伪临界温度(PCT)，PCT被认为是跨临界流动的关键参数[16]。图4给出了热流密度q为1 000 kW/m2、质量流速G为1 200 kg/(m2·s)、管径d为8 mm、入口温度Tin为280 ℃的条件下PCT的等温线(PCL)。

图3 水的物性参数随温度的变化率

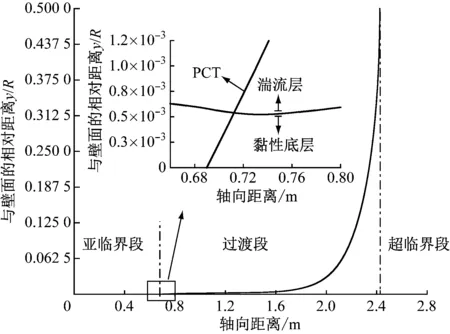
图4 水的跨临界区分段及PCT等温线

将局部雷诺数Rey=2 300时的壁面垂直距离y作为黏性底层的边界，根据黏性底层的PCL(见图4)可知，PCT由壁面上升至黏性底层边界所经历的轴向距离约为0.02 m，PCL附近极易引起黏性底层厚度和速度梯度的快速变化。在圆管中，当壁温Tw达到PCT时对应的轴向位置为过渡段的起点，当主流水中心温度Tc为PCT时，对应的轴向位置为过渡段的终点。黏性底层相对较薄，可近似认为边界层内的温度为Tw。

3.2 入口温度对黏性底层的影响

图5和图6分别给出在热流密度q为1 100 kW/m2、质量流速G为1 200 kg/(m2·s)、管径d为8 mm的条件下入口温度对黏性底层厚度和速度梯度的影响。在不同条件下,黏性底层厚度均先后出现峰、谷值。在亚临界段，当TwPCT时体积膨胀系数的变化率快速变为负值，近壁侧的流动加速效应逐渐减弱，黏性底层的厚度开始增大，直到Tw为481 ℃左右时黏性底层内外流体体积膨胀系数的差别几乎可以忽略。但由于流体密度不断减小，流体体积的增大使得主流水的流速增大，导致流体整体流速继续升高，黏性底层的厚度开始减小。黏性底层厚度峰值位置对应的温度称为黏性底层的超临界拐点(SupIT)。由于运动黏度还存在一定的增速，因此边界层厚度减小的速率大于密度变化率。入口温度只影响同一黏性底层厚度峰、谷值的轴向位置，而不影响黏性底层厚度的峰、谷值。

图5 不同入口温度下黏性底层厚度沿轴向的分布

图6 不同入口温度下黏性底层速度梯度沿轴向的分布

黏性底层速度梯度与边界层厚度的变化呈相反趋势，在壁温为PCT时速度梯度出现峰值，当壁温降至SupIT时又开始上升。值得注意的是，速度梯度在Tw≈380 ℃时出现快速上升的现象，该温度点称为亚临界拐点(SubIT)。

3.3 质量流速对黏性底层的影响

图7和图8分别给出了热流密度q为700 kW/m2、管径d为8 mm、入口温度Tin为280 ℃的条件下质量流速对黏性底层厚度和速度梯度的影响。

图7 不同质量流速下黏性底层厚度沿轴向的分布

在不同质量流速下黏性底层厚度先后出现谷值和峰值。随着质量流速的增大，流体升温速率下降，导致黏性底层厚度峰、谷值的位置向出口偏移。同时，质量流速增大导致黏性底层厚度的峰、谷值均减小，但峰、谷差值逐渐减小，质量流速达到1 300 kg/(m2·s) 时黏性底层厚度的变化几乎可以忽略。如图8所示，质量流速的增大使得SubIT处的速度梯度提高，当质量流速增大至1 200 kg/(m2·s)时可以认为速度梯度的谷值消失。

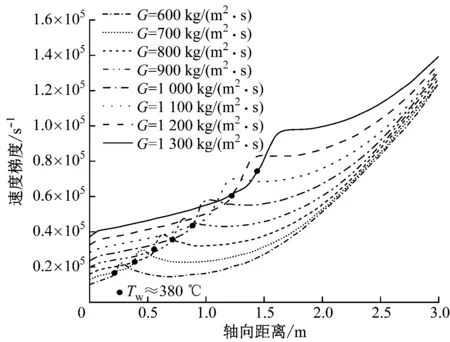
图8 不同质量流速下黏性底层速度梯度沿轴向的分布

3.4 热流密度对黏性底层的影响

图9和图10分别给出了质量流速G为1 200 kg/(m2·s)、管径d为8 mm、入口温度Tin为280 ℃的条件下热流密度对黏性底层厚度和速度梯度的影响。随着热流密度的增大，黏性底层厚度和速度梯度峰、谷值位置均向入口移动，黏性底层厚度峰值位置的变化趋势与图7相似，但谷值始终处于较低水平，且变化较小，在一定程度上代表了固定质量流速下跨临界区的最小黏性底层厚度。SubIT处黏性底层的速度梯度和速度梯度峰值与图6相似，热流密度的影响并不明显，但高热流密度使得SupIT之后的速度梯度具有较高的上升速率。

图9 不同热流密度下黏性底层厚度沿轴向的分布

图10 不同热流密度下黏性底层速度梯度沿轴向的分布

4 结 论

(1) 跨临界区水流动的黏性底层厚度并非单调变化，在壁温为PCT和SupIT处分别出现谷值和峰值；而速度梯度的变化则呈相反的变化规律，速度梯度在SubIT处加速提高，在壁温为PCT处出现峰值，速度梯度在SupIT处出现谷值。

(2) 入口温度、质量流速和热流密度均会改变黏性底层厚度的峰、谷值位置。其中，入口温度仅改变黏性底层厚度的峰、谷值位置，对其大小没有影响；质量流速的增大会同时降低黏性底层厚度的峰、谷值；热流密度增大会使黏性底层厚度的峰值增大，但不影响谷值大小。

(3) 入口温度、质量流速和热流密度均会改变黏性底层速度梯度的峰、谷值位置。其中，入口温度和热流密度仅改变速度梯度的峰、谷值的位置，对其大小没有影响；质量流速的增大会同时提高速度梯度的峰、谷值；热流密度对速度梯度的峰、谷值几乎没有影响。

(4) 黏性底层速度梯度决定了颗粒所受反向升力的大小，黏性底层厚度决定了反向升力的作用距离。黏性底层厚度和速度梯度越小,越有利于颗粒沉积。黏性底层厚度和速度梯度的谷值处更容易发生沉积，而且不同条件下黏性底层厚度和速度梯度的变化并不同步。