正交异性钢桥面疲劳分析方法研究综述

叶九发，翁怡军，衡俊霖

（1.中铁二院工程集团有限责任公司，四川 成都610031；2.深圳大学，广东 深圳518060）

1 概 述

正交异性钢桥面是通过纵肋、横肋和顶板3 种主要薄壁板件焊接形成的桥面系统，20世纪50年代开始广泛应用，至今已成为现代钢桥的重要标志[1]。伴随着焊接技术的进步和应用，正交异性钢桥面结构能使用相对较少的钢材，使其整体和局部具有较高的强度与刚度，且与传统桥面相比，其重量能减轻20%～40%。因此，正交异性钢桥面被广泛应用于各类桥梁中，包括不少大跨悬索桥和斜拉桥的主梁桥面。然而，历史上正交异性钢桥面的发展并非一帆风顺[1]，与其优异性能相对应的是反复交变车辆荷载作用下突出的疲劳问题。正交异性钢桥面存在以下特点：（1）构造较为复杂，应力集中现象严重；（2）大量采用焊接工艺，焊接残余应力大，存在潜在焊接缺陷的可能性大；（3）易疲劳细节数量大；（4）直接承受到车轮荷载的反复作用；（5）早期正交异性钢桥面焊接施工质量难以保证。在这些因素的共同作用下，正交异性钢桥面容易出现不同程度的疲劳裂纹[2]。

大量工程和科研机构对正交异性钢桥面的易疲劳构造细节进行了较为全面的疲劳试验。但是，疲劳试验的周期较长、成本较高，直接应用于工程实践的局限性较大。基于此，大量研究者基于数值模拟提出了各种形式的疲劳性能评价方法。总体上，可以分成：（1）宏观参数评价方法，即名义应力法；（2）局部参数评价方法，包括结构热点应力方法、局部应力法以及断裂力学法。本文就以上几种评价方法的原理和应用场景进行对比和综合研判，从而分析各类评价方法的优缺点及适用条件。

2 名义应力方法

名义应力法是目前应用最为广泛的疲劳评价方法。名义应力仅包含了构件的宏观几何形态在焊缝附近所带来的应力集中，未计入焊缝自身几何形态带来的局部应力集中[3]，可以看作是焊趾附近板件或者焊喉处的平均应力。通常，名义应力可以通过初等力学理论算得，对于较为复杂的细节，也可采用有限元方法计算名义应力，在利用有限元方法计算名义应力时，计算模型可采用较为简单的网格划分。同时，名义应力法是建立在已有疲劳试验数据的基础之上。现有疲劳试验数据大多以S-N 曲线的形式呈现。在疲劳试验中，大多数情况下选取板件表面上距焊趾一定位置的（通常为15 mm 或1.5 倍板厚）的测点应力作为构件的实测名义应力。

大多数规范[4-5]根据200 万次对应的疲劳应力幅将构造细节分为不同等级，在一定的保证率（通常为97.5%）下对疲劳试验数据进行回归分析，从而制订相应的S-N 曲线[4]。设计中在计算得到名义应力后，即可参考相应的S-N 曲线验算其疲劳强度。可以看出，名义应力法具有简单实用的特点，被广泛地应用于工程实践中，但名义应力法的评价需要相似细节的S-N 曲线作为支撑[6]。通常，S-N 曲线的获得需要进行系统的疲劳试验，从而消耗大量的时间和研究经费，而且疲劳试验中测试构件与实际构件也存在差异。这种差异难以量化分析，导致名义应力法的应用受到限制。

3 局部评价方法

名义应力法是一种简单实用的疲劳评价方法，但其评价的基础建立在对试验数据的统计分析之上，这就要求对特定的构造细节已有较为详尽的试验数据。同时，名义应力主要描述的是构件的宏观力学行为，在应用名义应力法进行疲劳评价时，需要根据设计规范或者指南中的描述，主观地选择构造细节所对应的疲劳强度等级，这一过程往往难以量化。为了克服名义应力法存在的缺点，基于局部力学参数的疲劳评价方法逐渐成为了研究的热点[7]。

近年来，大量研究者提出和完善了多种局部评价方法，大致可以分为以下3 类：（1）结构热点应力法；（2）局部应力法；（3）断裂力学法。以下将针对这几类方法的原理及其应用进行阐述和分析。

3.1 结构热点应力法

结构热点应力，早期也称作参考应力或者几何应力，是指结构构件中潜在疲劳失效处（热点）的一种虚拟应力[7]。焊接构件焊趾处的应力可以分解成3种形式：由轴力引起的膜应力σm、由板弯曲引起的弯曲应力σb、由焊趾形态引起的局部集中应力σnl（见图1）。其中，σnl表现为沿板厚方向分布的自平衡非线性应力。在热点应力σhs的计算中，仅计入膜应力σm和弯曲应力σb的叠加，而不考虑σnl的作用。通过长期的研究实践，热点应力法逐渐趋于成熟和实用。在IIW、CEN、API、AWS、DNV 等机构制定的规范中，热点应力法都得到不同程度的体现，同时也在不断的更新中。

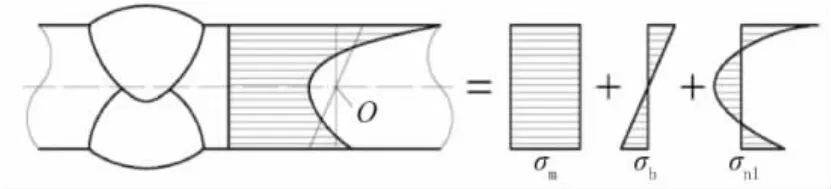
图1 焊趾处非线性应力分解

结构热点应力的计算建立在对焊缝构造细节的有限元分析之上，通过对分析结果进行后处理来得到热点应力σhs。根据定义σhs=σm+σb，计算中需要消除非线性应力σnl的成分。随着热点应力法的发展，出现多种计算方法，较具代表性的有：（1）IIW 建议的表面线性外推方法（LSE）[4]；（2）Radaj 等[8]推荐的沿板厚积分的方法（TTWT）；（3）Dong[9]提出的带剪应力修正的沿板厚积分方法（以下简称Dong 方法），3 种方法的计算原理见图2。

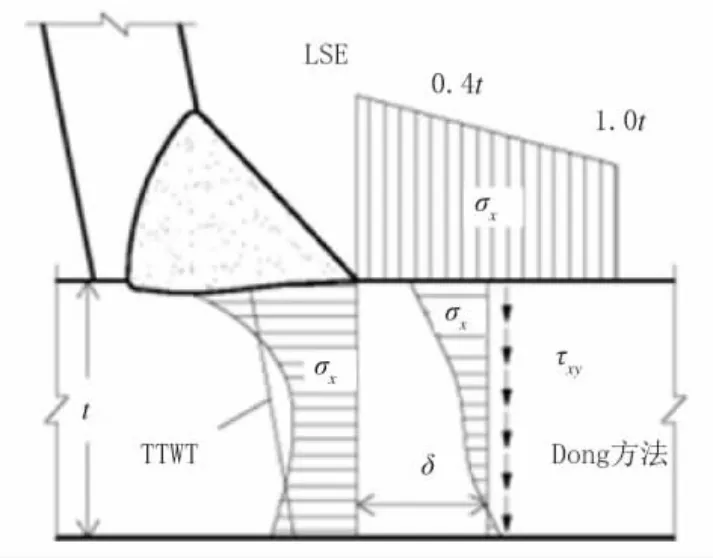
图2 3 种结构热点应力计算方法示意

表面线性外推方法的原理是通过对离焊趾一定距离的2 个或多个参考点的应力结果进行外推，来得到焊趾处的热点应力。最为常用的是基于0.4 倍板厚和1.0 倍板厚参考点的线性外推方法（也称作0410 方法），如式（1）所示：

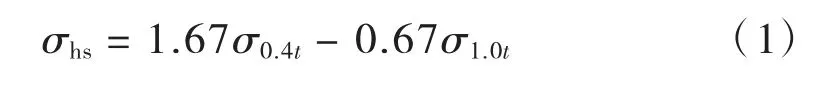
式中：t 为板厚；σ0.4t和σ1.0t分别为0.4 倍板厚和1.0倍板厚处的应力。

基于该方法，IIW[4]将常见焊接细节分为9 类，并将这9 类细节分别归纳为FAT 100 和FAT 90 这2个疲劳抗力等级。同时IIW[4]给出了较为详细的指南，包括网格划分、计算方法以及对应的参考热点应力S-N 曲线。

表面线性外推是一种简单有效的方法。但在某些局部应力集中非常明显的构造细节中，表面线性外推不能真实反应焊趾处的应力集中，同时该方法的计算结果受网格密度和荷载模式的影响较大[8]。基于此，Radaj 等[8]提出了在焊趾处沿板厚方向积分的方法（TTWT），将焊趾处沿板厚非线性分布的应力线性化，从而消除σnl成分的影响。Dong[9]在TTWT 的基础之上进行了修正，提出了计入剪应力影响的Dong 方法。该方法利用距焊趾δ 处截面应力与焊趾处截面应力的平衡关系，在热点应力σhs的计算中计入沿板厚分布的剪应力σxy的影响。在此基础之上，Dong 等[10]结合断裂力学方法定义了一种虚拟的“等效结构应力ΔS”，并提出了对任意焊接细节都适用的“主S-N 曲线”概念。试验表明，主S-N 曲线可以将离散的疲劳数据压缩到一个范围较小的分布带中[11]。

3.2 局部应力法

随着疲劳研究的深入和数值计算技术的发展，焊缝区域的局部应力开始被用于疲劳强度的评价，并逐步发展为一种新兴的疲劳评价方法，即局部应力法。局部应力法大多起源于缺口试件的疲劳评价方法，由于焊材与母材交界处（如焊趾和焊根）存在的几何形态突变可以被看作广义的缺口，因此焊接构件也可以作为缺口试件来进行疲劳评价[12]。局部应力法将局部区域应力状态作为评估参数，直接反映了局部应力集中程度，更加符合疲劳失效的力学机理。基于这一概念，目前已形成了多种成熟方法，较具代表性的包括：（1）IIW[4]推荐的等效缺口应力法；（2）Lazzarin 等[13]推荐的峰值应力方法（PSM）；（3）Taylor 等[14]提出的临界距离法（TCD）。

等效缺口应力法认为，缺口处的应力集中直接影响构件的疲劳性能[4]。因此，求解缺口处的应力状态对疲劳评价至关重要。然而，根据弹性力学理论和有限元方法，缺口处峰值应力存在奇异性，该处有限元解不收敛。Neuber[15]基于“微观结构约束理论”提出了通过引入一个虚拟的缺口半径ρf来对缺口处峰值应力进行平均化。根据文献[4]，Neuber 建议采用式（2）计算虚拟半径ρf：

式中：ρ 为实际缺口半径；S 为与多轴应力状态和强度准则相关的系数；ρ*为微观结构约束尺度。

Neuber[15]的研究表明，钢材的ρ*可以取0.4 mm。同时，Radaj[16]建议，在考虑米塞斯屈服准则的情况下，系数S 可取为2.5。在最不利情况下，即假设ρ=0，通过式（2）可以得知ρf=1 mm。根据上述理论，等效缺口应力法[4]在计算中引入了ρref=1 mm 的参考缺口半径，通过有限元等方法来求取缺口处的等效应力并将其作为疲劳性能评价的参数。IIW[4]对等效缺口应力法给出了较为系统的指南，并建议采用FAT 225 作为等效缺口应力法验算时钢结构焊缝的疲劳强度。

峰值应力法（PSM）由Nisitani 等[17]提出，最初用于求解椭圆孔洞处裂纹的I 型应力强度因子KI。Nisitani 等指出，I 型应力强度因子与峰值应力之比KI/σpeak仅与单元尺寸相关，在固定的网格模式下σpeak可用于KI的快速计算[17]。Lazzarin 等[13]将这一方法推广至焊缝的疲劳评价中，并给出了峰值应力σpeak与缺口应力强度因子NSIF 的换算关系。可以看出，峰值应力并没有作为一个独立的参数来进行试件的疲劳评价，而是作为计算缺口应力强度因子的一种手段。

临界距离法（TCD）认为，焊缝的疲劳强度不仅仅与缺口处最大应力有关，还受到距缺口周边一定范围内（即“临界距离LDv”）的应力场控制[18]。Haddad 等[18]结合断裂力学推导了临界距离的计算公式，其可视作与材料性能相关的常数，对低碳钢可近似地取0.4 mm。Talyor 等[19]建立了临界距离法的计算方法，并将其分为点法、线法、面法以及体积法。其中点法最为简单有效，其原理是通过有限元计算确定到缺口距离为LDv的点的应力状态并将其作为疲劳评价的参数[19]。文献[20]应用临界距离法中的点法和面法分析对接接头以及T 型接头焊缝疲劳性能，并与其他几类方法进行对比，结果表明点法较其他几种方法具有最佳的计算精度。

3.3 断裂力学法

断裂力学法[21]引入了应力强度因子的概念对缺口处局部力学行为进行描述。相比于传统方法，断裂力学法更接近于构件疲劳破坏的机理。根据计算方法和判别准则的不同，断裂力学法在疲劳评价中的应用方法又可分为2 类：裂纹扩展方法[4]和缺口应力强度因子法（NSIF）[13]。

裂纹扩展方法认为[21]，微裂纹的扩展过程占据了构件绝大部分的疲劳寿命。裂纹扩展方法假设构件初始存在长度为ai的微裂纹，其疲劳寿命近似等于微裂纹长度从ai扩展到最终长度af所花费的时间。根据Paris 法则[21]，裂纹扩展的速率与应力强度因子存在如式（3）所示的关系：

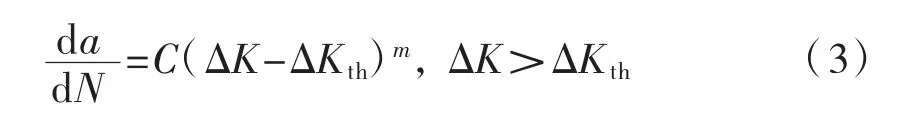
式中：ΔK 为循环中应力强度因子K 的变化幅值；a 为裂纹尺寸；N 为应力循环次数；C 和m 为与材料相关的常数。

根据Paris 法则，在确定每次循环中的ΔK 后，对裂纹长度a 进行从ai到af的积分即可得到对应的循环次数N[7]。应力强度因子K 的计算主要通过2 种方式进行：一种是采用近似公式进行计算，如IIW 建议的相关公式[4]；另一种是通过有限元软件建立带裂纹的网格模型，直接计算应力强度因子，如ANSYS 17.0 中采用的相互作用积分法[22]。基于裂纹扩展法，IIW[4]给出了较为详细的参数取值和应用指南，并建议采用裂纹长度达到板厚的一半作为疲劳破坏准则，即af=0.5 t。在应用数值方法进行裂纹扩展分析时，由于ΔK 与裂纹长度a 直接相关，对于a 的积分过程只能通过多次建模和计算近似完成[23]。

近年来出现一种新的裂纹扩展计算方法—扩展有限元法（XFEM）。扩展有限元法通过改进形函数的方法来引入裂尖富集函数，通过裂尖富集函数来描述裂纹问题中的不连续成分，从而实现对裂纹扩展的模拟[24]。与传统有限元方法不同的是，扩展有限元法在模拟裂纹扩展时无需建立带裂纹的网格模型，在模拟裂纹生长时也无需进行网格的重新划分。Nagy 等[25]应用扩展有限元方法对正交异性钢桥面中顶板—纵肋焊缝的疲劳裂纹扩展过程进行了全过程模拟，结果表明该方法在正交异性钢桥面的疲劳评估中具有较好的效果。

缺口应力强度因子法[13]认为，焊趾处可看作V型缺口，而焊根处可看作滑移型缺口。与裂纹扩展法相比，缺口应力强度因子法和传统的S-N 方法更类似。在确定缺口应力强度因子K 后，构件的疲劳评价需通过与K-N 疲劳抗力曲线进行对比来完成[7]。Lazzarin 等[26]对缺口应力强度因子法进行了推导和证明，给出如式（4）所示的表达式：

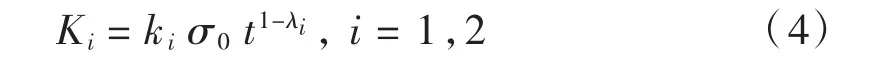
式中：i = 1，2，分别代表张开型和滑移型裂纹；σ0为名义应力；t 为板厚；λi为Williams 应力解中的特征值；ki为与焊缝形态和荷载模式相关的无量纲系数。

文献[13]利用缺口应力强度因子法对135°的角焊缝进行了分析，并与试验数据以及断裂力学等方法进行了对比，验证了缺口应力强度因子法的可行性。

4 各类评价法的优缺点

（1）名义应力法因具有简洁明了的特点，在工程领域中得到广泛应用。但是，名义应力法对试验数据的依赖性强，其评价精度受细节划分的影响较大。同时，由于名义应力采用较为宏观的力学参数进行评价，对局部效应不敏感，其结果具有较大的离散性。

（2）相比名义应力法，结构热点应力法能够更加真实地反映失效位置的应力状态，从而大幅提高评价结果精度。该方法在一定程度上具有局部法的特征，可显著减少细节分类的数目，进而有效降低离散性。同时，热点应力的计算仅需要在局部分析的基础上进行少量后处理，较为简单实用。但是，该方法为简化计算模型和降低网格敏感性，忽略焊缝自身几何形态和非线性应力的影响，不能完全反映焊缝的局部应力状态。

（3）局部应力法采用潜在疲劳位置的局部应力状态作为评价参数，相比于名义应力法和热点应力法更接近于疲劳破坏的机理。但由于缺口处（如焊趾和焊根）的峰值应力存在奇异性，不能将其直接作为评价参数。为解决该问题，大量研究者提出了不同的计算理论。其中，等效缺口应力法基于“微观约束理论”，在缺口处人为地设定一个虚拟的等效倒角半径，并详细规定网格的划分方法，从而实现峰值应力的平均化。此外，峰值应力法认为缺口处峰值应力与缺口应力强度因子的比率仅受到网格尺寸的控制。相应地，该方法通过规定缺口处的网格模式，实现通过峰值应力直接计算应力强度因子。与前述2 类方法不同，临界距离法认为，临界距离范围内的应力场直接影响焊缝的疲劳性能，故将该应力场的应变能参数作为评价指标。其中，临界距离是与材料性能相关的常数。

（4）断裂力学法在疲劳评价中的应用可分为裂纹扩展法和应力强度因子法2 类。裂纹扩展法假设构件中存在初始裂纹，构件的疲劳寿命近似等于微裂纹扩展成为疲劳失效裂纹的时间。缺口应力强度因子法认为，构件的疲劳性能与缺口处的应力强度因子直接相关。特别地，缺口应力强度因子法试图通过建立统一的K-N 关系曲线来进行疲劳评价，但由于其采用了断裂力学作为理论基础，缺口应力强度因子K 相比于名义应力和热点应力包含更多缺口处的焊缝几何形态和应力场信息。

5 结 语

（1）名义应力法和结构热点应力法为工程实践中的疲劳验算提供了切实可行的计算方法，其精度能够满足工程应用的基本要求。但这2 类方法对疲劳破坏机理的体现不够，且其评价都是建立在大量试验数据的支承之上。

（2）局部应力法和断裂力学法更加注重疲劳破坏的机理，且对试验数据的依赖程度较小，其评价结果在一定程度上能起到对疲劳试验的补充作用，但其分析难度和工作量较名义应力法和结构热点应力法显著增加，不宜直接应用于工程实践，更适用于疲劳机理研究和作为代替疲劳试验的数值评价方法。