微分法在有限元分析中的应用

王朝振，刘银涛，孙建鹏，周 鹏，孙文武，张家驹

（1.中铁建大桥工程局集团第三工程有限公司，辽宁 沈阳110000；2.西安建筑科技大学土木工程学院，陕西 西安710055）

0 引 言

有限元法自提出以来，就得到了广泛的关注。随着时间的发展与计算机技术的进步，有关有限元法的各种理论以及应用得到了不断补充与完善，同时与有限元法相关的各类通用和专用的CAE 软件也得到了广泛开发与应用[1-3]。如今有限元法已经形成了相当完善的计算体系，可以用来计算和模拟与结构相关的各类宏观以及微观力学介质问题。特别是有限元法作为一种成熟的结构分析方法[4-7]，被广泛用来求解众多工程问题的数值解[6-8]。

在结构分析中使用有限元法处理待离散结构时，其做法是采用基本单元将待离散结构划分为若干子单元，例如采用三角形单元，那么就会在所离散的每一个三角形上分别得到一个近似的插值近似函数，这个函数被称为形函数。形函数是针对单元内的插值而言的，一般指的是对单元内任意位置P，可以由单元所有节点（Pi）处的值进行插值而得到P 点的值，即Vp=N1×V1+ N2×V2+···+ Ni×Vi+···，其中Ni即为对应于Pi点的形函数，在数学上就是一种插值的权函数。

作为有限元法的基本特色之一，形函数的求解往往决定着有限元数值分析的准确性。Dasgupt[9]和Malsch 等[10]采用代数方法构造多边形单元的Wachspress 插值函数，给出了采用三角形面积表达的插值形函数公式；王兆清等[11]给出了多边形有限单元形函数的几何构造方法，并分析总结了Wachspress 插值、Laplace 插值和平均值插值的构造方法和性质；李术才等[12]通过采用平均值插值方法，提出了一种求解微分方程边值问题的多边形有限元方法；王丽等[13]采用面积坐标方法和形函数谱方法构造四边形薄板元，从而大大简化了新单元的推导过程，而且导出的高阶形函数非常简洁；夏晓舟等[14]基于复合函数链式求导法则，获得了三维自然单元法non-Sibson 插值形函数导数的显式格式，比现有的Lasserre法更简洁、直观，大大缩减了计算过程；崔梦雷等[15]采用拉格朗日插值法，针对全局坐标下结构的位移形函数进行了求解，结果表明得到的形函数求解简单，精度与常规逆变换相当。

虽然以上针对形函数的推导方法形式多样，也解决了现有结构分析中存在的各种隐性问题，但是仍然存在着很大的主观性，而且只能适用于性质相同的结构，造成公式的适应性很差。

采用解析式法能够很好地解决现有的有限元形函数适应性太差的问题。解析式法的基本原理是依靠现有的有限元原理以及结构的平衡方程构造等量关系式，并将其与现有的边界条件相结合，从而能够针对不同的问题采用同样的分析方式，解决形函数的重复推导问题，例如，傅向荣等[16]将有限元的离散法与解析法成果有机融合，给出了一个在弹性力学问题中构造独立完备解析试函数的通用方法；许晶等[17]采用解析式法重新构造了Timoshenko 梁有限元的位移形函数方程；许晶等[18]在考虑杆件扭转以及翘曲的情况下，采用解析式法，构造了全新的杆件扭曲位移形函数方程。

综上，本文基于有限元原理以及结构的平衡方程，提出了一种求解结构单元形函数的方法，此方法推导出的杆单元以及板单元的形函数不仅与现有公式相同，而且理论上可以用于推导任何结构的形函数，不仅大大简化了不同结构之间公式之间相互转换的麻烦，同时将有限元形函数的推导过程透明化，为有限元的进一步推广和拓展提供了一条行之有效的途径。

1 基本原理

1.1 结构平衡微分方程

工程结构是一种静定结构，根据冗余度的多少可分为静定结构和超静定结构。无论结构是处于静止状态还是运动状态，结构在任意时刻都满足平衡条件，或为静力平衡或为运动平衡。结构构件静力平衡的微分方程为：

式中：D 为构件的广义刚度；V 为构件的广义位移；n为阶数；p 为单位长度上的荷载。

1.2 微分方程的解析解

有限元法中的形函数反映了结构单元内部的位移模式。因此，形函数可以考虑为仅体现单元自身可能出现的变形特征。根据有限元原理，结构的荷载及变形均集中在节点上，单元内部并无与变形相耦合的荷载。此时式(1)可表示为：

微分方程（2）的解析解为：

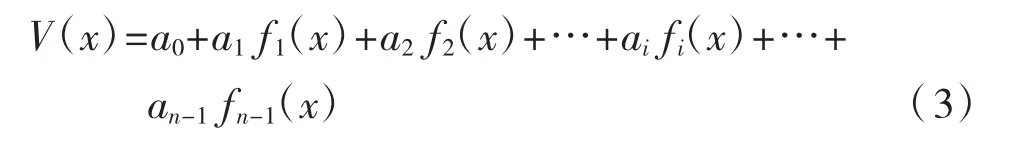
式中：ai（i=0，1，2，…，n-1）为待定常系数；fi（i=1，2，…，n-1）为已知关于x 的函数。

1.3 单元形函数

对于n 阶微分方程所对应的单元，必有n 个节点自由度与之对应。将节点自由度及节点局部坐标代入式（3），形成关于ai（i=0，1，2，…，n-1）的方程组：

式中：A 为关于ai（i=0，1，2，…，n-1）的待定向量组；F 为关于fi（x）（i=0，1，2，…，n-1；x=0，l）的已知函数值；l 为单元长度；U 为单元节点广义位移向量组。

根据式（4）就可以求得待定系数ai，将其代入式（3）并整理成关于节点广义位移的矩阵，即可得到相应单元的形函数，记为N（x）。即：

式中：δe为单元节点广义位移向量组。

2 实例

2.1 杆系单元

杆系单元根据受力特点可以分为两类，一类是只有轴向荷载和轴向变形的杆，另一类是受轴力、剪力、弯矩以及扭矩等共同作用的梁。杆单元的静力微分方程为：

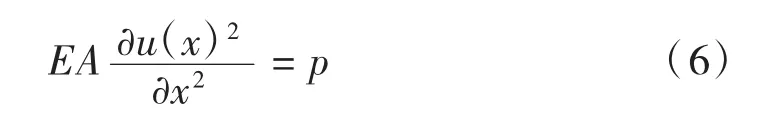
式中：E 为杆件的杨氏弹性模量；A 为杆件的截面面积；u 为杆件沿x 方向的位移。

令荷载p=0，式（6）变为：

式（7）可进一步表示为：

微分方程（8）的解析解为：

式中：C1、C2分别为待定系数。

根据杆件的边界条件，u（0）=u1，u（l）=u2。可以得到关于系数C1和C2的方程组：

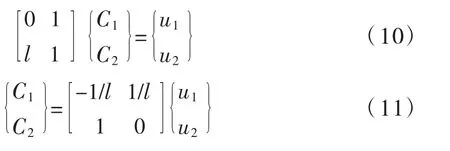
将式（11）代入式（9），可以得到单元广义位移与单元节点位移的关系式：

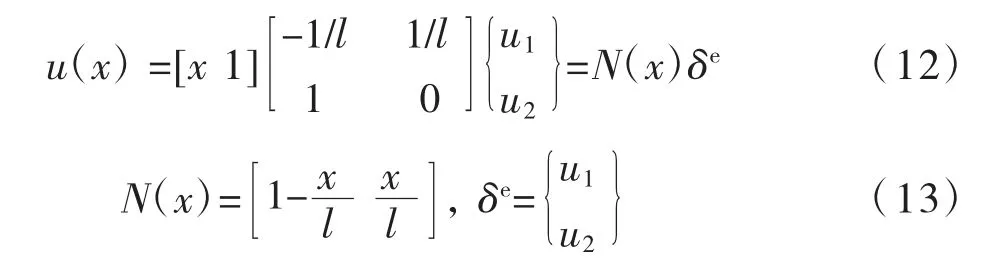
式（13）、式（14）均与文献[8]相同。

平面梁单元的静力微分方程为：

式中：I 为惯性矩。

同理，式（15）可进一步表示为：

微分方程（16）的解析解为：

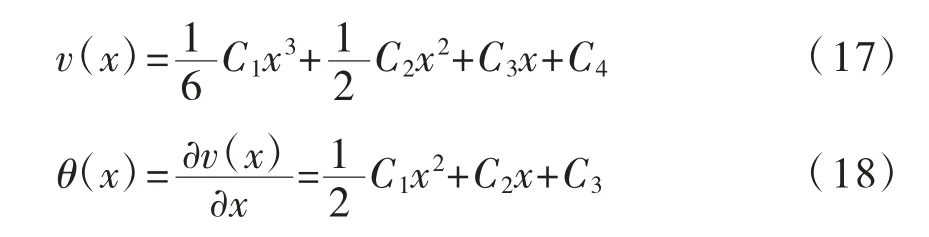
式中：θ（x）为转角，即挠度的1 阶导数。

根据梁单元的边界条件v（0）= v1，θ（0）= θ1，v（l）=v2，θ（l）=θ2，可 以 得 到 关 于 系 数C1、C2、C3、C4的方程组：

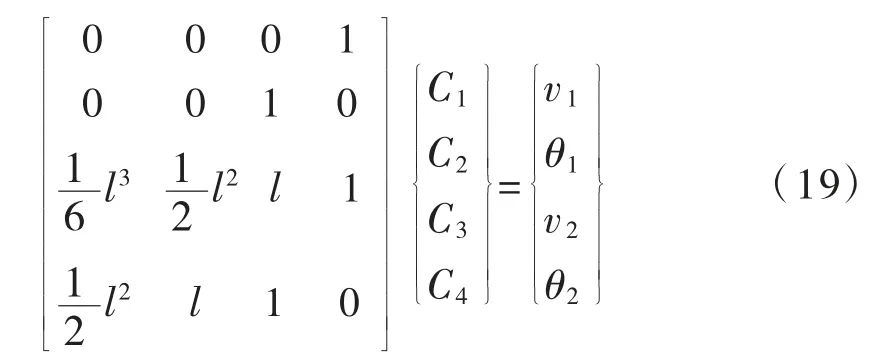
由式（19）可以得出:

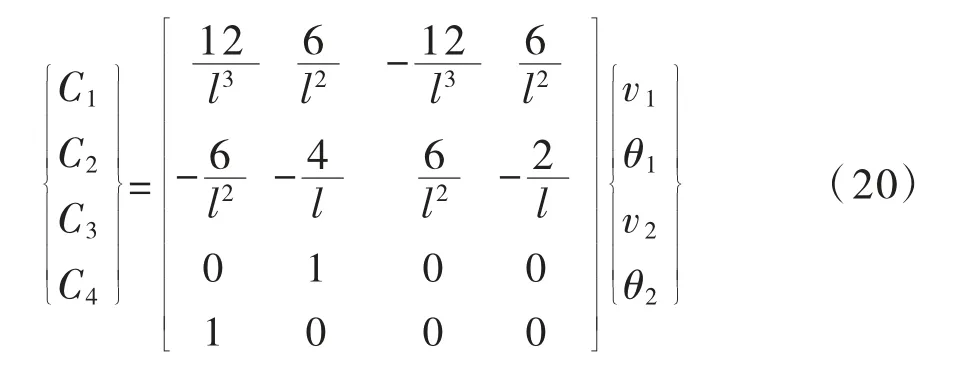
将式（20）代入式（17），可以得到梁单元广义位移与节点位移的关系式：

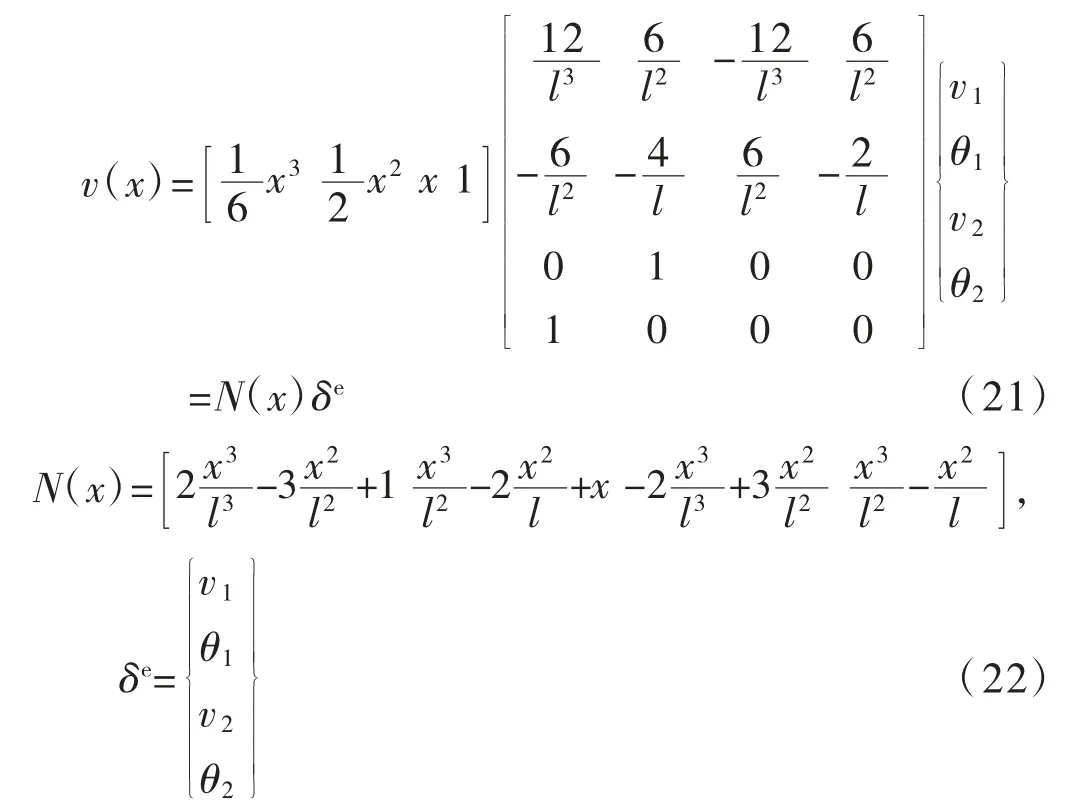
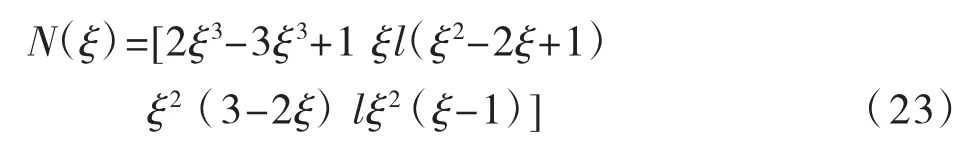
空间梁单元共包含4 个微分方程，分别为：

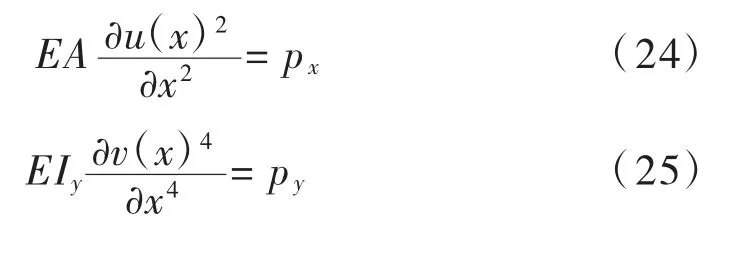
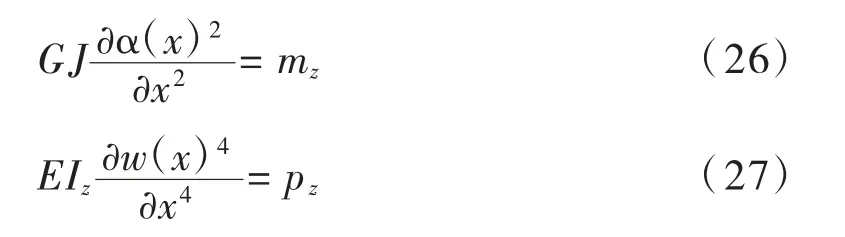
式中：Iy、Iz和J 分别为绕y 轴、z 轴的抗弯惯性矩和绕x 轴的扭转惯性矩；G 为剪切模量。

空间梁单元形函数为杆单元形函数和梁单元形函数的组合：

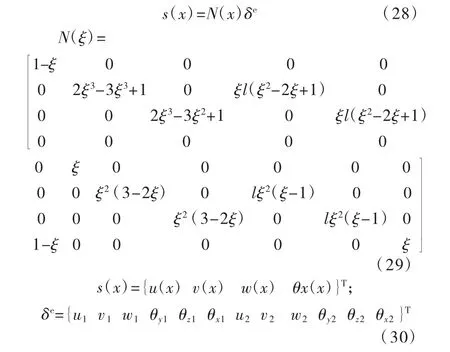
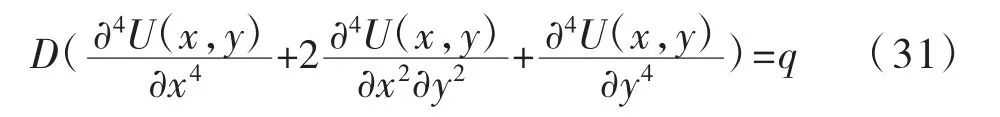
式 中：ui、vi、wi、θyi、θzi、θxi（i=1，2）分 别 为 沿x、y、z 轴方向的位移及绕y、z、x 轴方向的转角。

2.2 薄板单元

薄板单元的平衡微分方程为：（h 为薄板厚度，ν 为泊松比）；U（x，y）为板的挠度；q 为板受到的垂直板面的荷载集度。

对于矩形板单元，一般取4 个角点为节点，每个节点有2 个自由度。此时，薄板仅存在2 个坐标轴方向变形的相关项，则式（31）将简化为：

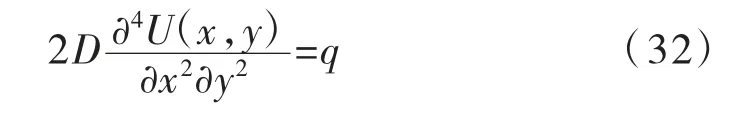
式(32)可进一步表示为：

微分方程(33)的解析解为：

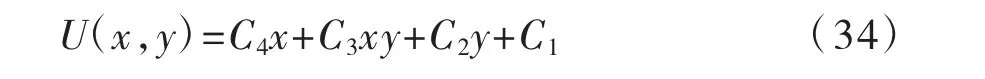
为了与节点位移相适应，式（34）可拓展为：

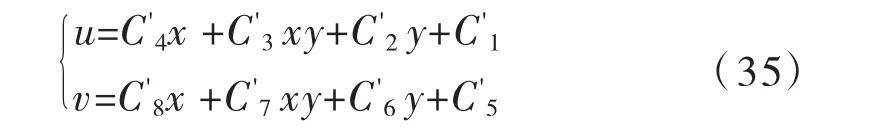
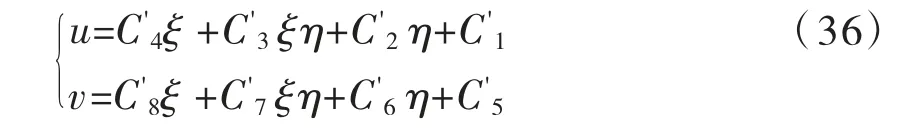
局部坐标系中节点的坐标分别记为：（ξ1，η1），（ξ2，η2），（ξ3，η3），（ξ4，η4）。将其代入式（36）可得：

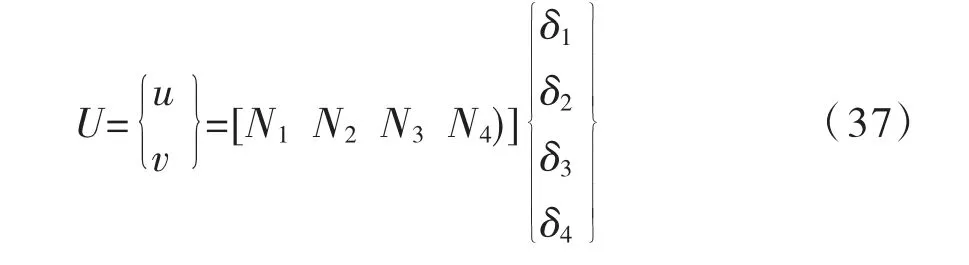
式中：Ni=（1+ξξi）（1+ηηi）/4 。

3 结 语

本文根据结构单元的微分方程，结合有限元原理，提出了确定单元形函数的理论解。推导了杆系单元、板单元的形函数。推导出的形函数与已有的形函数完全一致，表明本文提出的方法是有效的。该方法基于结构的微分方程，理论上可用于任何单元形函数的求解。同时为建立特殊单元的形函数，应用有限元原理求解特殊问题提供了一种新的方法。