临界平面多轴疲劳寿命估算模型的验证与评估
王肇喜 , 白 金 , 王海东 , 仇原鹰 , 李 静
(1.上海航天精密机械研究所,上海 201600;2.西安电子科技大学 机电工程学院,西安 710071)
0 引言
通常,将材料的多轴应变疲劳寿命估算模型分为3 类:第一类是静态屈服理论在复杂应力状态下的延伸即等效应变模型,第二类是基于塑性功理论的应力−应变乘积模型,第三类是基于临界平面上的应变或应力−应变组合模型[1-8]。这些模型分别建立在不同的多轴疲劳破坏准则上,文献[9-15]先后回顾并评述材料的多轴疲劳破坏准则。总的来说,等效应变法虽然在对比例加载下的多轴疲劳寿命预测表现出较好的预测效果,而在非比例加载下,由于应力−应变主轴旋转,一般不能给出较好的预测结果;但是由于等效准则简单实用,只需要测出一种应力条件下(如单轴拉压)的疲劳曲线,就可以预测各种多轴条件下的疲劳寿命,因此在工程实际中应用较为广泛。对于基于塑性功理论的寿命预测模型,虽然在某些情况下能成功描述材料的疲劳问题,但是塑性功是标量,不能反映裂纹萌生和扩展的优先平面。与等效应变法和塑性功理论方法相比,基于临界平面理论定义裂纹萌生和扩展的优先平面,具有一定的物理意义,但是临界平面的定义、损伤参量的选择、表达形式的构建等都会影响模型寿命预测结果的精度。文献[1,6-8,16-20]也分别利用不同临界平面模型估算不同材料不同情况下的多轴应变疲劳寿命;然而,对于同一对象不同模型估算结果的对比,或者不同对象同一模型估算结果与试验结果的对比,研究报导较少。
考虑到临界平面模型众多但篇幅所限,本研究仅限于对比分析不同常用临界平面模型的估算结果,并对其进行讨论,在此基础上,指出今后应该研究的问题。利用不同类型材料、不同形状试件的多轴疲劳试验数据,对常用临界平面模型进行试验验证,并分析各模型的优缺点和适用性,为基于临界平面理论寿命预测模型的工程应用提供理论支撑。
1 估算多轴疲劳寿命的临界平面模型
疲劳失效的主要原因是临界剪切面上的交变剪应力,次要原因是垂直于该平面的正应力,同时,材料属性、应力状态、工作环境及应变幅值等也对疲劳有影响;因此,Findley[21]提出临界平面的概念,Brown-Miller[22]进一步发展这一概念,并根据疲劳裂纹形成的机理进行物理解释。Brown-Miller 从试验中发现,在多轴交变载荷作用下所形成的典型裂纹有2 种−A 型、B 型。对于A 型,中间主应变ε2垂直于自由表面,裂纹为沿着表面扩展的浅长裂纹;对于B 型,最小主应变ε3垂直于自由表面,裂纹向纵深方向扩展。2 种可能的裂纹起始形式根据不同的损伤参量,可以得到不同的临界平面损伤模型,典型的有如下6 种:
1)剪应变模型。其定义具有最大剪应变幅平面为临界平面,以Δγmax/2 为损伤参量,相应的应变寿命关系为[23]:
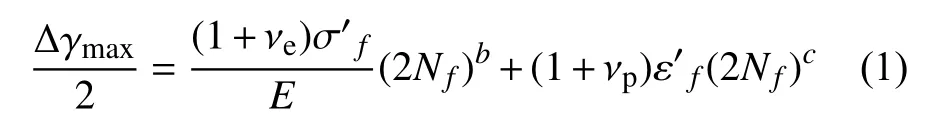
其中,νe、νp分别是弹、塑性泊松比。和分别为疲劳强度系数和疲劳延性系数,b、c 分别为疲劳强度指数和疲劳延性指数。 Δγmax是最大剪应变范围,E 是弹性模量,Nf疲劳寿命。
2)Wang-Brown 模型。Wang 等考虑平均应力影响,引入法向应变变程提出以下寿命估算模型[5]:
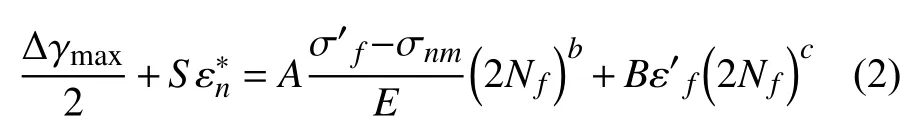
其中:S 为材料常数, A=(1+νe)+(1−νe)S ,B=(1+vp)+(1−vp)S ,S 值缺乏时可取为0.3; σnm是临界平面上的法向平均应力。
3)SY 模型。尚德广等[8]认为,Brown-Miller 所提出的临界平面法的一般形式为法向应变与剪切应变分量经过一个加权后的代数和,从连续介质力学的观点来看是很难给出物理解释的,且其中常数有时并不是固定不变的,因而估算多轴疲劳寿命有时会产生很大的误差。他们认为,如果将临界平面定义为具有最大剪切应变的平面中具有最大法向应变的平面,其面上的最大剪切应变幅是疲劳损伤的真正驱动力,利用von-Mises 准则将临界平面上 Δ γmax和法向应变变程两参数合成一个等效应变幅,则可得到一个拉伸形式的多轴疲劳损伤参量,并用其作为临界平面上的损伤控制参量,表达式为:
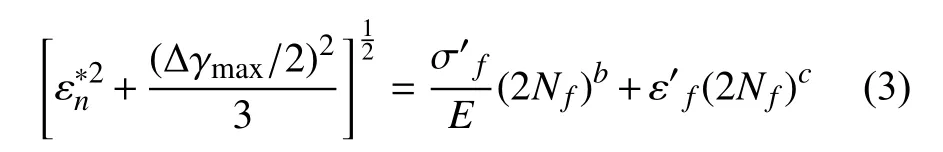
4)Fatemi-Socie 模型。Fatemi 等[2]认为合适的损伤参量应同时考虑正应力和剪应变的影响,提出以下模型:

其中: Δ γmax、σn,max分别为临界平面上的最大剪应变范围和最大法向应力,σy是屈服强度,G 是剪切模量,σn,max考虑非比例加载所引起的附加硬化的影响,材料参数k 反映不同材料的正应力对疲劳寿命影响的敏感程度,k 值缺乏时可取为1。和分别为剪切疲劳强度系数和剪切疲劳延性系数,b0和c0分别为剪切疲劳强度指数和剪切疲劳延性指数。
5)Smith-Watson-Topper 模型。Socie 对Smith-Watson-Topper 模型[4]进行修正,定义最大正应变幅平面为临界平面[24]。该模型认为在多轴情况下,最大法向应力 σmax与最大正应变幅 Δεmax/2的乘积是一个合理的损伤参量,表达式为:
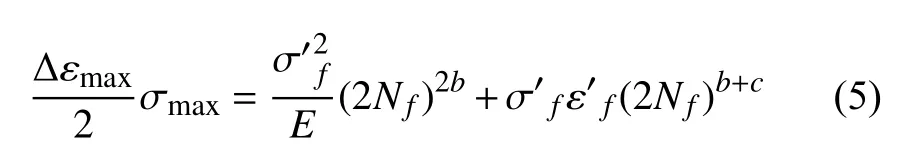
6)Brown-Miller 准则。Brown 和Miller[22]认为最大剪应变幅和最大剪应变面上的法向应变幅的线性组合是一个合适的损伤参量。Socie[24]用临界平面上的法向平均应力 σnm对BM 模型进行修正,得到如下关系:
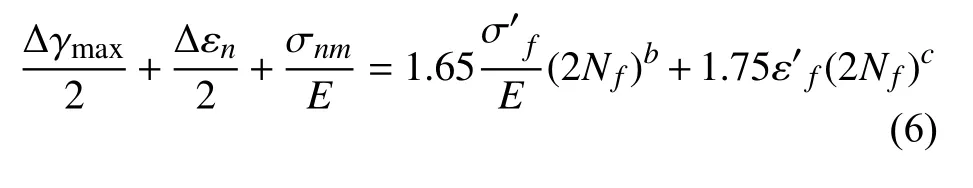
2 模型验证及评述
2.1 模型验证
引用1045HR 钢[2]、45 钢[25]、S460N 钢[26]3 种材料在各种比例和非比例加载路径下的疲劳寿命试验数据对Sines 和Ohgi 提出的最大剪应变准则[23](SO 准则)、Wang-Brown 准则[5](WB 准则)、尚德广准则[8](SY 准则)进行评估。引用AISI316 不锈钢[18],LY12CZ 铝合金[27]多轴疲劳试验数据对Fatemi-Socie 准 则[2]( FS 准 则) 、 Smith-Watson-Topper 准则[4,24](SWT 准则)以及Brown-Miller 准则[22,24](BM 准则)进行验证。其中,前3 种材料均为薄壁圆管试件,后2 种材料均为缺口试件,材料参数分别见表1、表2,验证结果见图1。缺口材料的应力应变计算结果取自文献[28]。
由图1a~图1c 可以看出,最大剪应变准则、SY 准则、WB 准则对45 钢的预测结果基本分布在2 倍因子以内。对1045 钢、S460N 钢比例加载下的预测结果也比较准确,基本位于2 倍因子以内,但是对其非比例加载下的预测结果,大部分都偏于危险一侧,相比较而言,SY 准则偏于危险一边的程度要小一些。
由图1d~图1f 可以看出,BM 准则对AISI316不锈钢的预测结果偏于危险一侧,而对LY12CZ铝合金的预测结果却比较保守。FS 模型不论对AISI316 不锈钢还是对LY12CZ 铝合金,预测结果都比较理想,大多数预测结果都位于3 倍误差带以内。SWT 准则不管对AISI316 不锈钢还是对LY12CZ 铝合金,预测结果都过于保守,所有预测结果都位于3 倍因子以外。
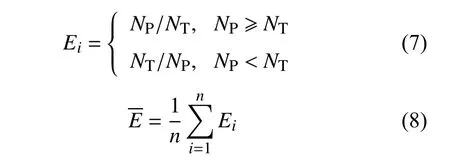
其中,NP是预测寿命,NT是试验寿命,n 为寿命个数。各疲劳寿命估算模型在比例和非比例加载下的预测结果平均误差因子见表3、表4。
由表3、表4 可以看出,对于薄壁圆管试件,比例加载下各疲劳寿命估算模型预测精度都比较令人满意,相比之下,在非比例加载情况下预测结果就比较差。对于缺口试件,SWT 模型估算寿命与试验寿命相差甚远,最大偏差达到126 倍因子;BM 模型的预测结果次之,最大偏差达到5.43 倍因子;FS 模型的预测结果最优,最大偏差为2.42倍因子。综合所评估的6 种临界平面模型而言,FS 模型可以给出较好的预测结果。
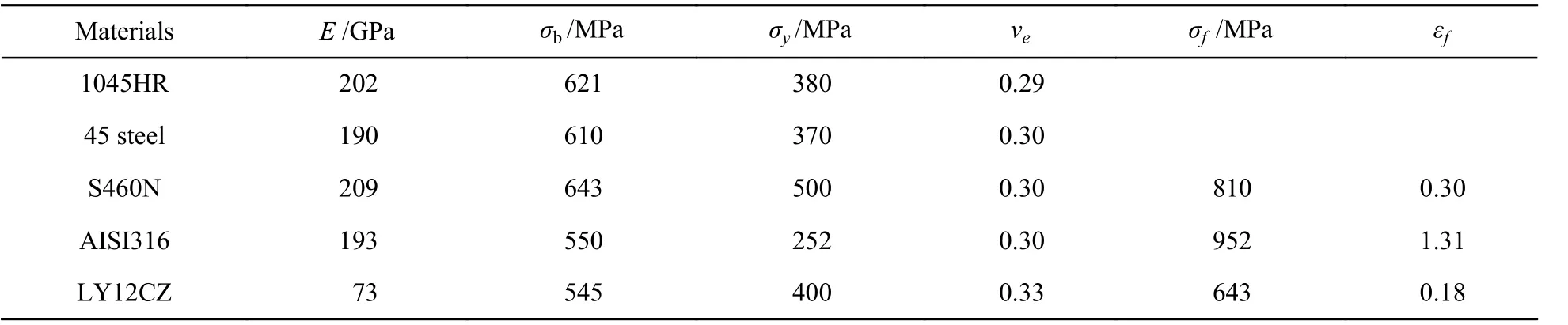
表1 材料的力学性能Table 1 Mechanical properties of the materials

表2 材料的单轴疲劳性能Table 2 Uniaxial fatigue properties of the materials
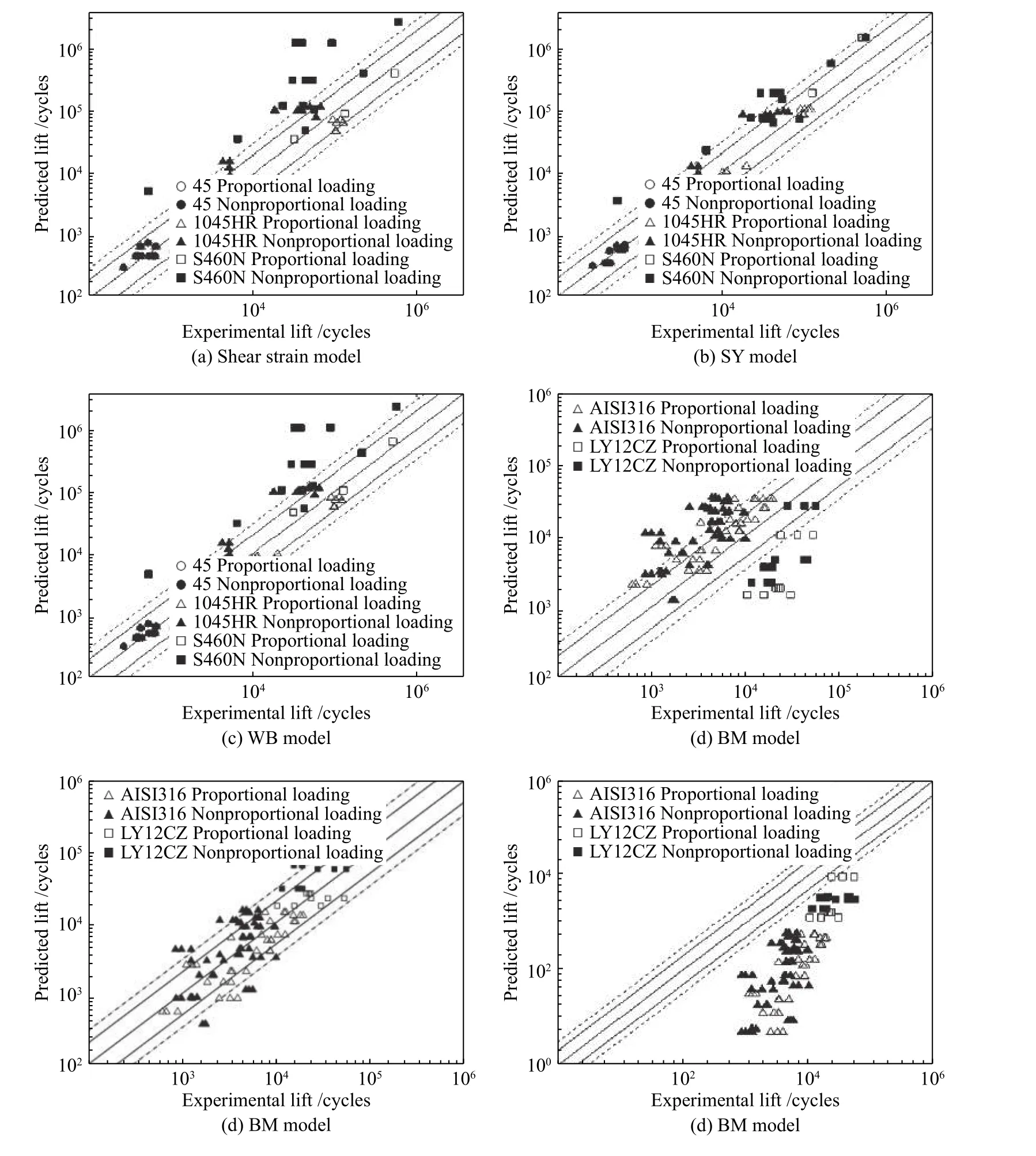
图1 模型试验验证Fig.1 Model test verification
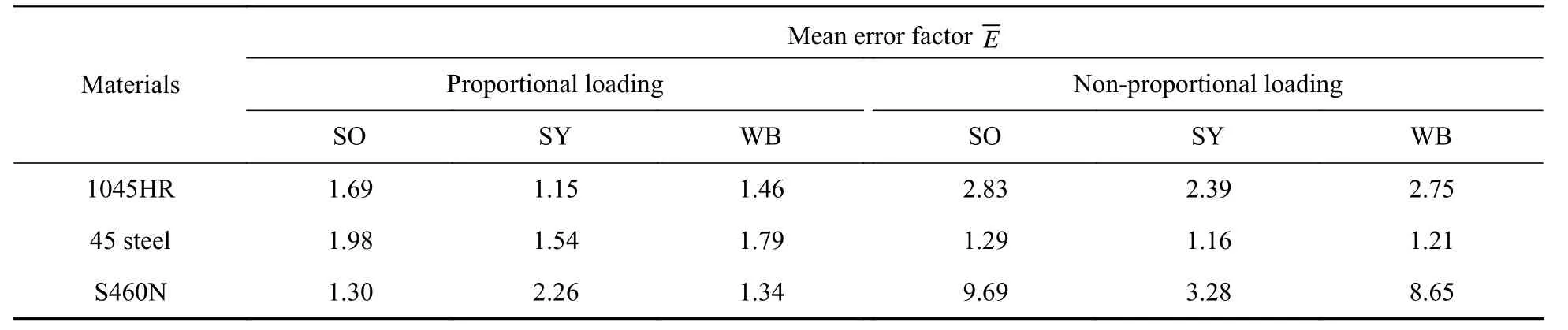
表3 应变疲劳寿命估算模型对光滑试件预测误差比较Table 3 Comparison of prediction errors of strain fatigue life estimation models for smooth specimens

表4 应变疲劳寿命估算模型对缺口试件预测误差比较Table 4 Comparison of prediction errors of strain fatigue life estimation models for notched specimens
2.2 模型评述
利用5 种材料对6 种常用临界平面寿命预测模型进行验证可以发现,对于同一对象,不同模型的估算结果相差较大;而对于不同对象,同一模型的估算结果有时低于试验结果,有时却高于试验结果。不同寿命预测模型估算寿命合理与否,一方面取决于预测模型中的疲劳损伤参量是否有效,另一方面也取决于预测模型的表达形式是否合理。
对于SO 模型、SY 模型和WB 模型,图1a~图1c 可以看出非比例加载下的寿命预测结果都偏于危险一侧。原因在于,这3 种模型的疲劳损伤参量都是基于应变,没有考虑应力对疲劳损伤的影响;因此,这3 种模型都不能很好地反映非比例加载引起的附加强化现象对疲劳寿命的影响。已有研究[2,24]表明,相同等效应变下,非比例加载引起的附加强化现象会大大缩短材料的疲劳寿命。由于SO 模型、SY 模型和WB 模型对非比例附加强化现象反映的不够充分,因此非比例加载下通常会给出偏于危险的预测结果。
另外,对比式(2)、式(3)左侧可以发现,对于SY 模型、WB 模型而言,两者引入的疲劳损伤参量相同,但是模型的表达形式不同。由此导致二者具有不同的疲劳寿命预测结果,见图1b、图1c。整体而言,非比例加载下SY 模型的预测结果要优于WB 模型的预测结果。原因在于,WB 模型采用临界平面上的法向应变变程与剪切应变范围经过一个加权后的代数和,从连续介质力学的观点来看是很难给出物理解释。与之相比,SY 模型利用Von-Mises 准则将临界平面上的法向应变变程与剪切应变范围合成一个等效的损伤参量更为合理;由此可知,选择何种表达形式来描述材料的疲劳损伤是十分重要的。
对于BM 模型、FS 模型、SWT 模型,3 个模型中的损伤参量都引入应力项;因此,与SO 模型、SY 模型和WB 模型相比,这3 个模型在某种程度可以更好地反映非比例附加强化现象对疲劳寿命的影响。但是,由图1d、图1f 可以看出,BM 模型、SWT 模型的预测结果并不理想,原因主要有以下几个方面:
由式(6)可见,BM 模型的损伤参量中引入临界平面上的法向平均应力σnm来反映平均应力对材料疲劳寿命的影响。本研究中采用的1045HR钢[2]、45 钢[25]、S460N 钢[26]3 种材料,不管是比例加载工况还是非比例加载工况,都不存在明显的平均应力;因此,对这3 种材料而言,在文献[2,25-26]的加载工况下,临界平面上的平均应力σnm近似为0。此时,BM 模型与材料常数S=1 时的WB 模型相类似,也不能很好地反映材料的附加强化现象。由图1d 可见,BM 模型一方面高估AISI316不锈钢的疲劳寿命,另一方面又低估LY12CZ 铝合金的疲劳寿命。验证结果表明,临界平面上的法向应变范围与剪切应变范围的代数和并不是一个合适的多轴疲劳破坏准则。
对于SWT 模型,Socie[24]指出该模型适用于拉伸型破坏材料;但是,试验发现不管是AISI316不锈钢还是LY12CZ 铝合金,都是剪切型破坏材料。这是造成SWT 模型预测结果不理想的重要原因之一。对于FS 模型(图1e),不管是AISI316不锈钢还是LY12CZ 铝合金,都给出较为理想的预测结果。Fatemi 等[2]指出,FS 模型用于剪切型破坏材料。因此,FS 模型的适用范围与AISI316不锈钢和LY12CZ 铝合金的开裂形式相一致。这是FS 模型预测结果比较理想的原因之一。材料发生疲劳断裂之后,根据材料断口的形貌特征,能够确定材料的开裂形式,但是疲劳裂纹开裂形式不仅与材料类型有关,而且还与试验温度、加载幅度、加载路径等因素有关[24],判断在什么样的工况下材料属于剪切型开裂,什么样的工况下材料属于拉伸型开裂,目前尚未有明确的判断准则。由图1e、图1f 的试验验证结果可知,根据加载工况判断材料的开裂方式,对于合理选择疲劳寿命预测模型,提高疲劳寿命预测的可靠性至关重要。因此,借助试验手段,进一步研究疲劳裂纹开裂形式与材料类型、试验温度、加载幅度、加载路径等因素之间的关系,对于选择合适的多轴疲劳寿命预测模型,提高模型的预测精度,具有重要意义。
3 结论
1)对同一对象,不同模型的估算结果相差甚远,而对于不同对象,同一模型的估算结果有时低于试验结果有时却高于试验结果,是由于所验证的6 种模型都是特定材料在特定载荷状态下的产物,损伤参量及其中的修正系数都是对特定材料及特定载荷状态而言的。
2)对于6 种常用临界平面模型,比例加载下大多可以给出较好的预测结果,但是非比例加载下,各模型的预测结果差异较大。综合看来,FS 模型对于剪切型开裂材料具有较好的预测精度;但是,目前如缺乏多轴疲劳试验数据,材料的开裂形式难以准确判断,进一步研究能有效预测多轴非比例疲劳寿命的预测模型仍具有重要意义。

