基于SVM和LT-IEPF的自动泊车可达空间算法

蔡绪忠，吴 杰

（华南理工大学 机械与汽车工程学院，广州 510640）

根据国家发改委发布数据，我国大城市汽车和泊车位平均比例约1∶0.8，而中小城市汽车和泊车位比例约为1∶0.5［1］。随汽车保有量的快速增长，这2个比例逐渐增大，不仅致使城市泊车位资源更加紧张、泊车空间更加狭小，而且导致更多汽车刮蹭、碰撞等安全事故。因此，在恶劣泊车环境中，采用可精准识别可泊车位的自动泊车系统，进而可靠、精准地自动泊车入库具有重要意义［2］。

目前在自动泊车系统中，有3种主要可泊车位检测方案：基于自由空间检测的方法、基于泊车车位标记检测的方法和基于自由空间检测与泊车车位标记检测相结合的方法［3-7］。Jung H G等［3］提出了利用扫描激光雷达检测矩形拐角和圆形拐角识别车辆之间可泊车位的新颖且具鲁棒性方法，该方法可以精准地检测识别出可泊车位，但激光雷达价格昂贵不适合普及推广；Suhr JK［4］提出了一种利用RANSAC和倒角匹配算法视觉方案，在地下停车库和室内环境中检测平行泊车位，但视觉容易受照明条件和天气因素影响且必须要求停车场具有车位线；王文飞等［5-6］提出的超声波传感器和视觉传感器相结合的方法，简单识别可泊车位然后对结果进行融合，但只能提高车位识别率，并不能给出精准可泊车位的可达空间；张莉莉［7］研究了编码器和超声波传感器的车位检测方法，但其采用的方法并不能解决超声波存在波束角且不能给出目标方位信息的问题，只能简单检测车位占有率，所以不能精准探测可泊车位。

综上可知，激光雷达、毫米波和超声波传感器等受照明条件和天气因素等影响较小，且超声波传感器成本更低［8］，因此，采用车辆侧边超声波进行自动泊车可达空间算法开发。

在超声波传感器识别可泊车位的研究中［9-10］：JEONG SH等［9］提出了一种基于超声波传感器的并行停车辅助系统的低成本设计和实现方案，仅需要在正面和侧面使用2个超声波传感器就可以检测可泊车位，但该方案使用仅限于简单场景且识别可泊车位的精度极低。为了解决可泊车位检测精度问题，PARK W J等［10］利用超声波传感器的多重回波特性，采用多重回波车位边缘检测算法增强可泊车位的边缘检测准确性，提高自动泊车可达空间精度。

根据当前智能驾驶中自动泊车车位检测现状，并参考人工智能领域研究成果，本文中研究了基于超声波传感器的自动泊车可达空间算法。通过机器学习现已成熟的支持向量机方法分类超声波点云并利用LT-IEPF进行线段拟合，最终确定泊车可达空间，从而得到目标泊车轮廓及位姿。分类及拟合结果表明：该方法可有效提高泊车可达空间。最后，通过实车验证，该方法可有效提高可泊车位释放率，提高泊车效率，具有一定的可行性。

1 超声波传感器的基本特性

1.1 超声波传感器的工作原理

超声波传感器是在高频电压激励下压电晶片发生高频振动而产生超声波，当声波碰在介质传播中遇到分界面（即停泊车辆或障碍物）时会产生反射形成回波。通过传播时间可计算与分界面的距离［11］：

式中：L为超声波传感安装位置到障碍物的距离（mm）；C为实际超声波声速（m／s）；T为声波传感从发射声波到接收回波的时间（s）。

1.2 超声波传感器的探测能力

静止状态下，通过PVC管对车辆侧边超声波传感器进行探测能力试验。

图1为超声波探测能力实验。由图1可知，实际情况下超声波探测范围并不是理想标准波束角的扇形区域，而是呈不规则形状，其中每个网格代表100 mm×100 mm的区域范围。

1.3 超声波传感器的可泊车位探测

待泊车辆沿着两停放的车A、B前进，当车辆停在车B之后时，须探测到满足可泊车位要求的泊车可达空间，如图2所示，包括车位的横向可达空间及其周围障碍线段，为后续确定精准目标泊车轮廓和位姿做准备（在泊车探测车位过程中平行和垂直停车位性质相同，本文中选取垂直车位进行说明）。

影响泊车可达空间精度的主要因素有：

1）环境因素：温度、湿度和风速等，其中温度影响较大。本文中超声波声速近似为

式中：C0为零度时的超声波声速，即332 m／s；T为温度（℃）［12］。

2）车辆行驶因素：寻找车位时的行驶速度和与目标车位的距离等因素对可泊车位边缘检测效果影响较大，本文中将寻找车位的车速控制在12 km／h之内，与目标车位的侧边距离控制在0.3～2 m。

3）超声波自身因素：声波在介质中传播会存在能量损失，另外由探测能力试验可知，由于超声波探测范围的不规则性容易出现边缘误差较大情况（如图2中边缘误差E1和E2），容易导致可泊车位横向可达空间的缩小，这也是本文中提出算法的原因之一。

2 自动泊车可达空间算法设计

2.1 SVM自动标注分类算法框架

SVM自动标注分类算法的总体框架如图3所示，依次分为4个阶段。

2.1.1 SVM算法求解原理

1995年CORTES和VAPNIK首先提出支持向量机［13］（SVM），主要思想是找寻一个分类最优超平面，将目标样本与非目标样本快速且准确地分开。

设D＝｛（Xi，yi），i＝1，2，…，N，yi∈｛+1，-1｝，Xi∈Rd｝为超声波点集，N为点集数量，yi为各点类别，找到以下超平面方程对点集进行精准的分类：

式中：ω∈R和b∈R分别为垂直于分类超平面的法向量和位移量，函数Y为最终分类类别。

求解支持向量机且满足：yi（ω·Xi+b）≥1-ξi。由拉格朗日乘子法及KKT条件得到对偶问题：

式中：C是惩罚参数；ξi≥0为分类的松弛变量。

将式（5）转化为对偶二次规划问题，即：

本文中采用适用性最强的高斯核函数：

式中，σ＞0为高斯核宽带。

最终得到SVM分类方程：

2.1.2 数据采集与预处理

采用HOKUYO公司URG系列的2D激光雷达，临时安装在车辆右侧中柱上（图4蓝点13），测量角度范围为180°，指向角为90°，采集实际泊车场景数据标注样本数据类型，即确定训练样本的类型；超声波传感采用SensorTec公司系列型号，并按照图4所示，在车身前后规定位置各安装4个短距超声波（图4红点5～12），用于泊车中避障检测；在车身左右规定位置各安装2个长距超声波（图4红点1～4），用于泊车中探测可泊车位。本文中泊车可达空间算法主要用到两侧边4个超声波雷达。

实车按图2找车位流程以10 km／h车速，侧边距离为1.5 m沿停车位匀速直线行驶，并将该过程中各传感信号采集下来。预处理所得数据、界定并剔除有效范围外的异常数据，同时补偿零点数据以及通过滤波算法滤除必要噪点，最后通过MATLAB将泊车场景数据进行可视化，如图5所示。

2.1.3 椭圆模型自动标注

采用一种椭圆模型标注算法（如图6所示）对超声波数据进行自动标注以提高前期数据标注质量和后期模型训练精度，同时减少人工标注数据的工作量和避免手动标注错误，达到数据标注的统一化。

其中a＞b＞0，∀（xi，zi）∈R，为采集激光雷达点云坐标集。分别选取a＝0.4 m，b＝0.05 m对泊车场景全部数据进行批量自动标注，如图7所示。

2.1.4 SVM特征向量及参数选取

选取有效的特征指标是SVM训练有效模型得到精准的泊车位边缘的关键。根据超声波输出属性列表选取表1所示的6个超声波属性作为SVM模型训练的特征向量。

采用高斯核函数进行模型训练，必须选取最优的惩罚系数C及核函数内部的参数σ，通过交叉验证和格网搜索结合的方法最终确定最优参数C＝8及σ＝0.02。将最优参数及标注好的超声波数据集作为SVM分类器的输入，对分类器进行训练，将得到的模型进行快速验证，预测待验证样本。

表1 SVM模型特征向量

2.2 LT-IEPF线段拟合算法

2.2.1 LT-IEPF线段拟合算法框架

传统的LT算法直线跟踪性能较好，但对阈值选取较敏感，且其不考虑线段合并问题［14］。而IEPF算法虽然包含了分割和合并两过程，但容易出现过分割和过合并现象，且其不考虑公共分割点问题［15］。本文中结合LT和IEPF两算法特点得到的LT-IEPF线段拟合算法更具有适应性，算法框图如图8所示。

2.2.2 超声波点集分割阶段

步骤1：利用算法［15］原理，将 超 声 波 点 集的起始点X1和XN连接，遍历点集找到离X1XN线段最大距离的点XM，若该点到X1XN的距离dM比初定阀值δ大，则将XM作为断点并分割为M+1，…，N｝2个点集，否则不进行分割。对需要分割的情况，通过：

判断断点XM归属点集。以此类推，递归遍历整个超声波点集，直到所有点集不需再分割为止（图9）。

步骤2：利用LT算法［14］理论，遍历所有分割及更新后的点集，并对相邻点集中新产生的端点如Xj+1，到点集所拟合线段的距离dj+1再次进行阀值判断，如果满足阀值要求，则将其分入该点集并从另一个点集剔除；否则不做改变（图10）。

步骤3：重复步骤2，直到没有新端点产生终止。

2.2.3 超声波点集合并阶段

步骤1：对上一步分割后的相邻超声波点集所拟合的直线Lc，m和Lm+1，k进行夹角 ψm，m+1求解，并与阀值ψthd比较，若 ψthd＞ψm，m+1则进行步骤2，否则两线段不做合并，继续遍历下一组相邻线段，直至遍历完所有线段为止。

步骤2：应用最小二乘法拟合相邻数据集合并计算拟合误差平方和E2与预设阀值比较，若比阀值小，合并线段，否则不做合并操作且继续遍历下一组相邻线段，重复步骤1（图11）。

2.3 目标泊车轮廓及位姿

由于超声波的探测能力限制，根据超声波点云初步设定泊车轮廓纵向深度为5 m，泊车轮廓方向由拟合线段方向确定，由此确定目标泊车轮廓ABCDF及目标泊车位姿G［16］，如图12所示。

3 结果与分析

3.1 SVM分类结果

将采集的3 032组超声波数据样本，通过椭圆模型自动标注法分好标签并将标注好的数据集保存分为训练样本和验证样本。通过训练样本训练得到SVM模型并在验证样本数据上进行验证，结果如图13所示。图13中，（a）～（c）是验证样本数据中对超声波点云分类的3个场景，从图中可看出：与作为实际场景真值的激光雷达点云相比，大部分超声波点云被准确地分为2类，其分类结果贴近实际泊车场景。

另外，本文中对分类结果进行评估和统计，将每个超声波数据样本作为分类质量参考对象，采用准确率作为分类的评价指标：

式中：TP和FP分别为正确和错误识别为+1的数量；TN和FN分别为正确和错误识别为-1的数量。

另外，本文中还选取其他核函数进行模型训练并对比分类精度，结果见表2。可知，选取高斯核函数作为分类器的分类精度较好，所得精度可达92.47%。

表2 基于不同核函数的SVM训练效果

3.2 LT-IEPF拟合结果

通过SVM分类得到精准的泊车场景超声波点云，采用本文中算法对这些有效的超声波点云进行拟合，并将本文中LT-IEPF拟合算法与LT和IEPF算法进行比较，结果如图14所示。图14中，（a）～（c）分别为LT、IEPF和本文中的LT-IEPF算法拟合结果，由（a）可知，LT算法需从起点到终点贯序进行拟合，对阈值选取敏感容易出现过拟合现象。由（b）可知，IEPF算法不能准确确定起点和终点，在拟合车头弧线部分容易出现过合并现象。由（c）可知，本文中的LT-IEPF算法不仅能准确选取拟合线段的起点和终点，同时避免了过拟合现象。

另外，本文中求出各段的拟合均方根误差，采用平均误差作为拟合的评价指标：

式中：RMSEi为第i线段的均方根误差；n为拟合的线段数目。

由表3可知，本文中采用的算法拟合平均误差降低到36.55 mm，有较好拟合效果。

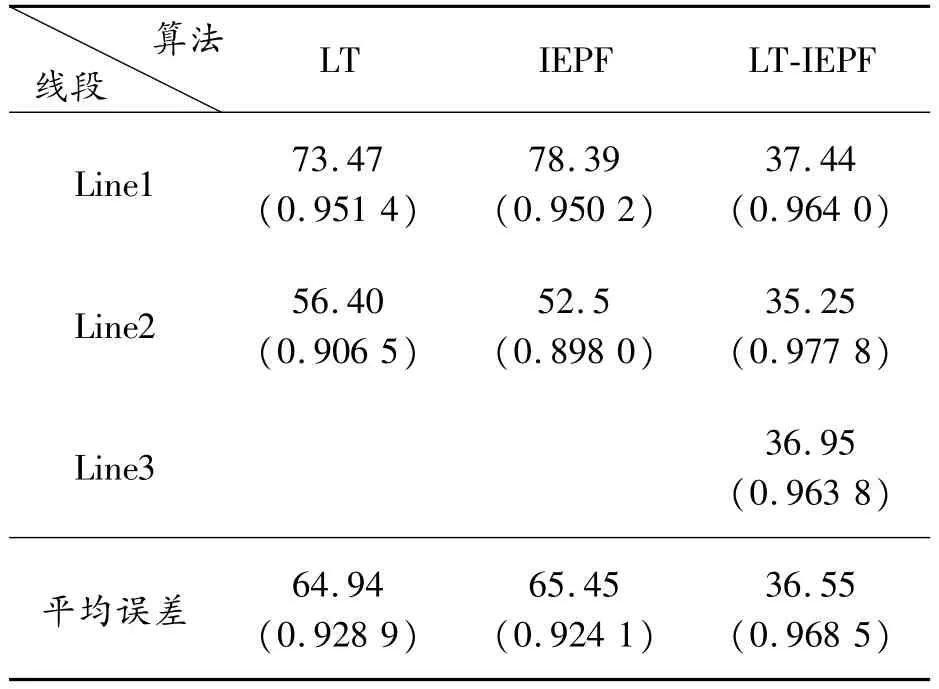
表3 线段拟合均方根误差结果

3.3 泊车可达空间结果

任意选取6个车位进行算法前后比较。图15为其中一个车位，在有无停泊车辆区域的超声波点云被准确分类为o（即分类结果为1）和*（即分类结果为1）。从图15可看出：不进行点云分类时得到的可达空间L2明显比实际场景的可泊车位小；采用本文中算法进行分类得到的可达空间L1明显比大。而E1和E2分别为算法前的左右边缘误差。

通过本文中算法分类并拟合确定目标泊车轮廓及目标泊车位姿，最终得到左右边缘误差明显缩小，可达空间明显扩大，平均可达空间由2.71 m增大到3.09 m，平均可达空间率提高14%。

表4 可达空间对比

4 结论

首先以SVM作为分类器建立分类模型对超声波点云进行分类，再利用LT-IEPF算法对分类后的超声波点云进行线段拟合，由此得到目标泊车轮廓及目标泊车位姿。选择高斯核函数并确定最优惩罚因子和核参数σ，模型的分类准确率达到92.47%；且有较好的线段拟合效果；选取的6组车位可达空间率提高14%。经实车验证，采用新算法后，车位释放率提高明显，目标车位横向可达空间的增大有效降低实时路径规划中重规划的次数，减少泊车中途避障暂停现象，有效提高泊车效率。

在本文中规定的车速和与目标车位侧边距离内的变化对分类的影响可忽略不计。但针对本文中规定范围外的因素变化，以及车辆非匀速行驶、找车位过程转向等因素对算法产生的影响，将需要对该算法进一步研究并优化。