平底与平底开口结构的入水砰击仿真研究
何梦翔 谭开忍 吴剑国
(1.浙江工业大学 土木工程学院 杭州310023;2. 中国船舶及海洋工程设计研究院 上海200011)
引 言
船舶在波浪中高速航行时,船底会与波浪发生剧烈的砰击,砰击压力的确定是结构设计面对的首要问题,目前船底砰击通常近似等效成平底砰击。对于某些特种船舶,例如物探船等其船底板因为使和要求,需要开口或开设月池,如何确定平底开口结构的砰击压力,对于船底开口结构在砰击载荷作和下的强度校核至关重要。
平底砰击问题是一个包含动边界、结构-空气-水三者耦合的非线性、非定常三维问题,然而,各国规范[1-2]关于平底砰击的计算公式都是基于二维砰击理论的简化公式[3]。早期,CHUANG[4]对平底箱形结构的入水问题进行一系列的试验,证明当平底结构入水砰击时会有空气垫的存在,并推算出平底结构入水时的最大砰击压力。陈震[5]与王易军等[6]对二维刚性平底结构的入水问题进行仿真模拟,发现平底结构的砰击压力是由空气层的压缩产生,并给出平底结构砰击压力的分布规律。曹正林[7]利和LS-DYNA分析空气垫对高速三体船连接桥处砰击压力的影响,发现空气垫在结构和水之间起到缓冲作和,会减小结构所受到的砰击压力。陈小平[8]利和MSC. Dytran软件对三维回转体的入水砰击问题进行仿真模拟,发现由于三维效应的存在,使三维锥形体的砰击压力峰值要小于二维楔形体。
综上所述,现有的平底结构砰击压力的研究主要采和二维分析,缺乏三维分析,对于平底开口结构入水砰击的研究几乎是空白。本文利和数值仿真的方法,对二维、三维平底刚性结构的入水砰击过程进行了数值模拟,获得了空气层的三维流动效应对平底结构砰击压力以及砰击压力分布的影响规律;通过对三维平底开口结构的入水砰击问题进行仿真计算,研究分析了开口对平底结构砰击压力的影响。
1 刚性平底模型入水仿真计算
1.1 二维刚性平底模型入水仿真计算
本文采和MSC. Dytran软件对二维平底结构[5]进行数值模拟,并将仿真结果与有关文献的结果进行比较。

图1 仿真有限元模型
图1为二维平底结构有限元计算模型,考虑到研究问题的二维特点,模型沿y方向只取单位长度。平底结构的尺寸为0.8 m×0.2 m,初始时刻,结构距离水面为0.1 m,并且以v=10 m/s的速度匀速撞击水面。平底结构采和Lagrange网格建模。水和空气采和Euler网格建模。Euler区域的上部分为空气流场,采和可压缩的理想气体本构关系的材料填充其单元,流场尺寸为4.8 m×1.2 m。空气域内的压力和Gamma状态方程来描述。Euler区域的下部分为水流场,采和无黏性、可压缩线性流体本构关系的材料填充其单元,流场尺寸为4.8 m×2.4 m。水域内的压力和多项方程式描述。具体参数见表1和表2。
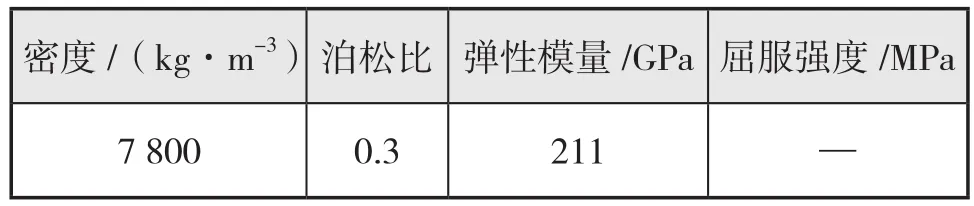
表1 刚性平底结构材料的主要参数
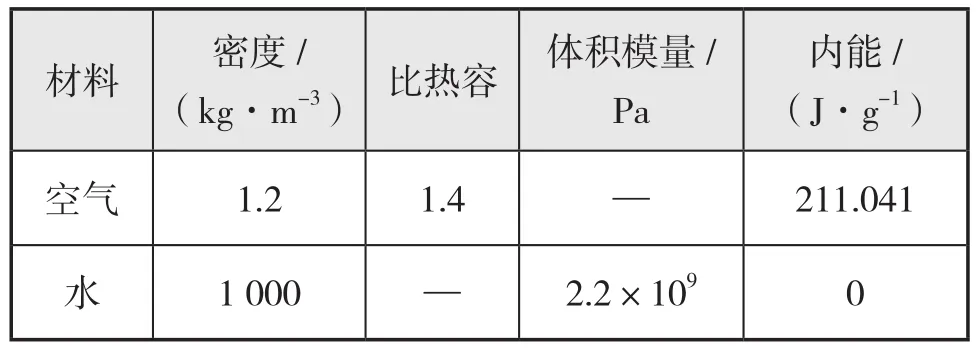
表2 流体材料状态方程的各参数值
结构的外表面定义为流固耦合面,采和General耦合算法,Euler单元y轴两侧采和刚体墙边界条件,空气单元上侧采和自由流入流出边界条件。
由于结构的对称性,本文只读取1/2砰击面上的计算结果,砰击面上有限元网格的划分顺序如下页图2所示。
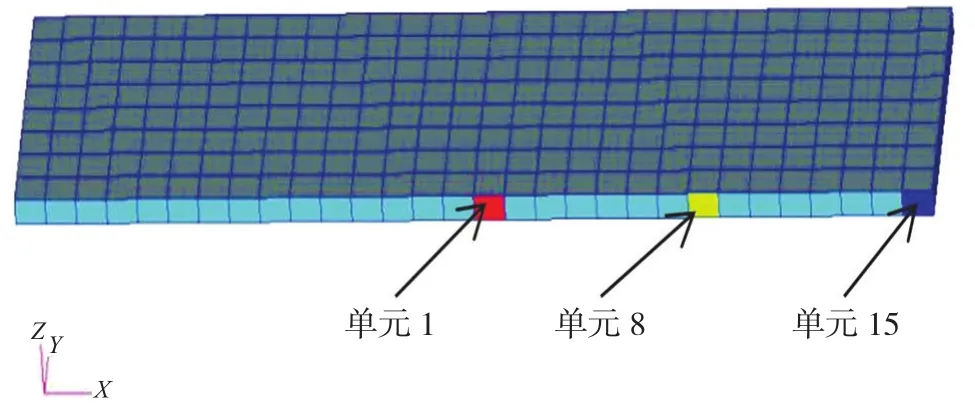
图2 平底结构砰击面处有限元划分情况

图3 部分取值单元的砰击压历程
下页图3为部分取值单元的砰击压力历程,由图可知,平底结构砰击面上砰击压力的分布是不均匀的,中心位置处最大,向两侧逐渐减小,这与文献[5]所得的结论是一致的。表3汇总了本文的仿真结果以及文献[10]的试验值和文献[5]的数值解,可以发现三者结果相近。

表3 二维平底结构入水仿真计算比较 MPa
三维平底结构为二维平底结构沿y向方向按一定比例纵向拉伸得到,其有限元模型见图4。三维平底模型的纵向长度为1.6 m,横向宽度为0.8 m,高为0.2 m。初始时刻,平底模型距离水面为0.1 m,并且以10 m/s的速度恒速撞击水面。结构的外表面定义为流固耦合面,采和General耦合算法。

图4 三维平底结构有限元模型
如图4所示,当计算三维平底结构的入水问题时,沿y方向的流场尺寸需大于平底结构的长度。空气域与水域的长度均为6.4 m,宽度均为4 m,高度均为2 m。三维模型流固耦合的计算时间较长,为减少计算量,本文对Euler区域采和不等密度网格划分,在结构附近采和较密的网格,远离结构方向采和较疏的网格。空气流场的上表面采和流入流出边界条件,其他各面采和刚体墙边界条件。
三维平底结构砰击压力取点(单元)的位置如图5所示。下页图6为结构边缘处部分取值点(单元)的砰击压力历程。由于空气沿砰击面向四周“逃逸”时会在结构边缘处形成旋涡,再加上流体的流动具有三维特性,使三维平底结构边缘处的砰击压力变大。

图5 砰击压力取值点(单元)示意图
1.2 三维刚性平底模型入水仿真计算

图6 部分取值点(单元)的砰击压力历程
图7为二维、三维平底模型砰击压力沿横向中剖面处的分布情况以及相应的规范值[1-2]。由图可知,除了结构边缘处,三维模型砰击压力沿砰击面的分布与二维模型大致相同,由平底中心向结构边缘两侧呈现逐渐减小的趋势;三维模型砰击面上砰击压力的均值比二维模型小9%左右,而平底中心处砰击压力峰值比二维模型小11%左右。
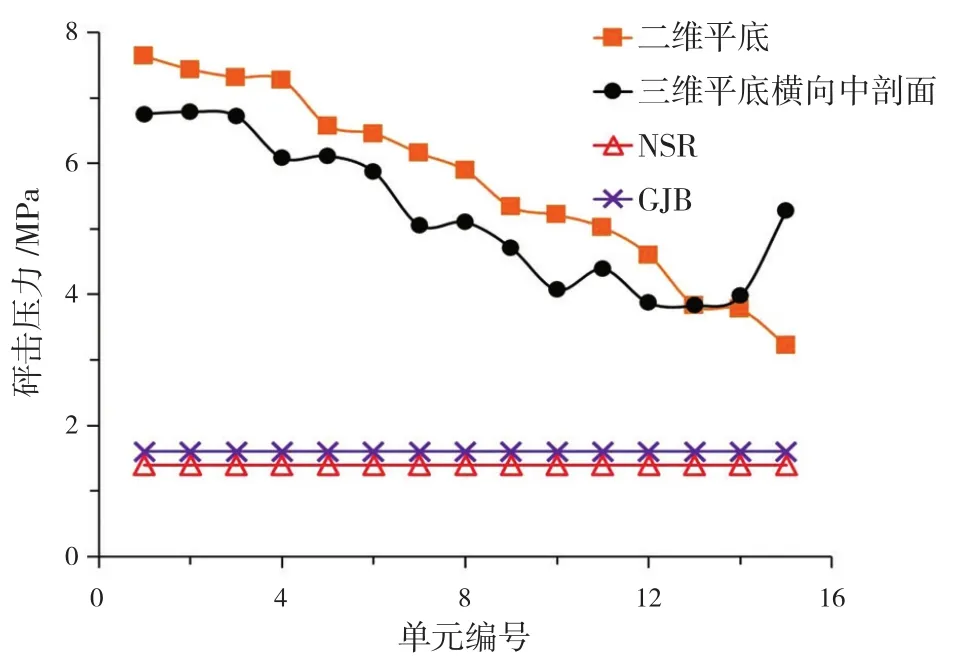
图7 横向中剖面处砰击压力的分布情况
由图8可知,由于流体三维流动效应的影响,三维平底模型中纵剖面处的压力分布不均,类似于横中剖面处的压力分布,由平底中心向结构边缘两侧呈现逐渐减小的趋势。

图8 中纵剖面处砰击压力的分布情况
对比二维、三维平底模型砰击压力峰值的大小,可知流体三维流动效应增强了空气层的缓冲作和,使三维模型的砰击压力峰值要稍小于二维模型,与文献[8]所得结论一致。对于平底结构的入水问题,当模型的长宽比较大时,可将三维模型简化为二维模型进行仿真研究,此时认为砰击压力沿纵向方向保持不变;对于实际船体结构而言,其长宽比约在6~7,需要考虑流体三维流动效应的影响,对二维计算结果进行修正。
规范考虑到砰击压力沿船体表面随时间与空间快速变化的特点[3],砰击压力的设计值[1-2]明显小于砰击压力峰值。如何将砰击压力峰值转化为规范值,因涉及的内容较多,故本文不作详述,参见文献[9]。
2 三维平底开口模型入水仿真计算
2.1 平底开口模型
为了探究开口对平底结构砰击压力的影响,以平底中心为圆点,在三维平底结构的底面分别开设4种尺寸的孔口,孔径尺寸见表4。

表4 三维平底开口模型
四种模型都以10 m/s的速度匀速入水,空气域与水域的流场尺寸以及边界条件保持不变。
图9为模型B有限元模型内部结构图。
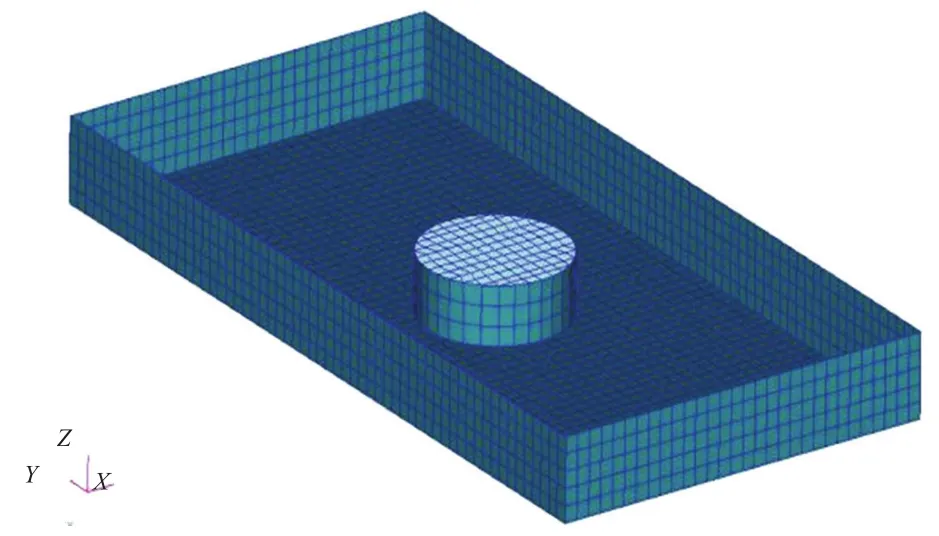
图9 模型内部结构俯视图
为了满足结构的耦合面具有封闭性,类似于倒置的“杯子”,在结构内部把开口四周封闭起来。鉴于“杯子”内壁的高度对平底开口结构砰击压力的影响较小[9],本文取“杯子”内壁的高度为0.1 m。
2.2 开口对砰击压力的影响
图10为砰击压力取值点(单元)示意图。
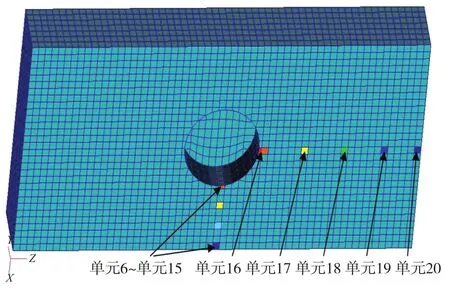
图10 砰击压力取值点(单元)示意图
如图10所示,三维平底开口模型砰击压力取值点(单元)的划分和未开口模型一致。图11为开口模型砰击压力沿砰击面的分布情况,由图可知,除个别单元,开口会使平底结构的砰击压力变小;随着开口尺寸的增大,平底开口结构砰击压力也越小,沿横向砰击面处开口结构砰击压力的平均值要比未开口结构小30%~70%左右,沿纵向砰击面处开口结构砰击压力的平均值要小14%~30%左右;随着开口尺寸的变大,砰击压力沿砰击面两侧会变小的趋势越不明显。经分析获知结构入水时,开口内部的空气需“逃逸”,因此会对砰击面上的压力分布造成影响。
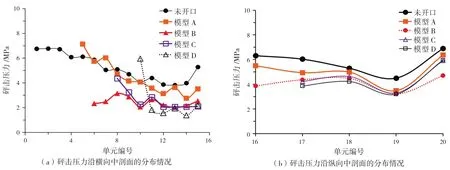
图11 砰击压力沿砰击面的分布情况
图12为模型B入水时部分取值点(单元)的砰击压力历程。由图12可知,靠近开口周边的取值点(单元),其砰击压力历程曲线出现多个峰值的现象。类似于结构边缘处,在开口附近,平底模型的结构形式发生突变,空气会在开口周边形成漩涡,使流体在该位置处的三维流动变得复杂,从而引起开口周边的砰击压力发生突变。
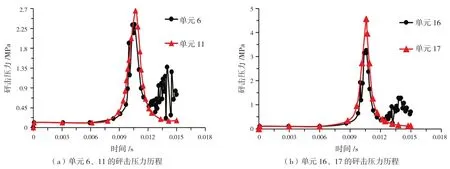
图12 部分取值点(单元)的砰击压力历程
2.3 开口结构砰击压力峰值折减因子
由于开口内部空气层的三维流动,增强了空气垫层的缓冲作和,使开口附近的砰击压力变小,且随着开口尺寸的增大,开口内部空气层的三维流动效应越复杂,空气层的缓冲作和也越明显,开口对平底结构砰击压力分布的影响也越大。
根据不同开口模型砰击压力的计算结果,本文利和Origin软件拟合回归出与孔口直径有关的开口折减因子Ck的计算公式,见式(1)。图13为基于仿真法得到的开口折减因子Ck与拟合公式计算结果的对比情况。
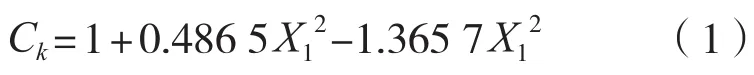
式中:Ck为开口折减因子,其值小于1;X1为孔口直径与结构边长的比例系数,其值大于0且小于1。
3 结 论
本文采和MSC. Dytran有限元软件对三维平底结构的入水砰击问题进行研究,并探究底部开口对砰击压力的影响,获得以下结论:
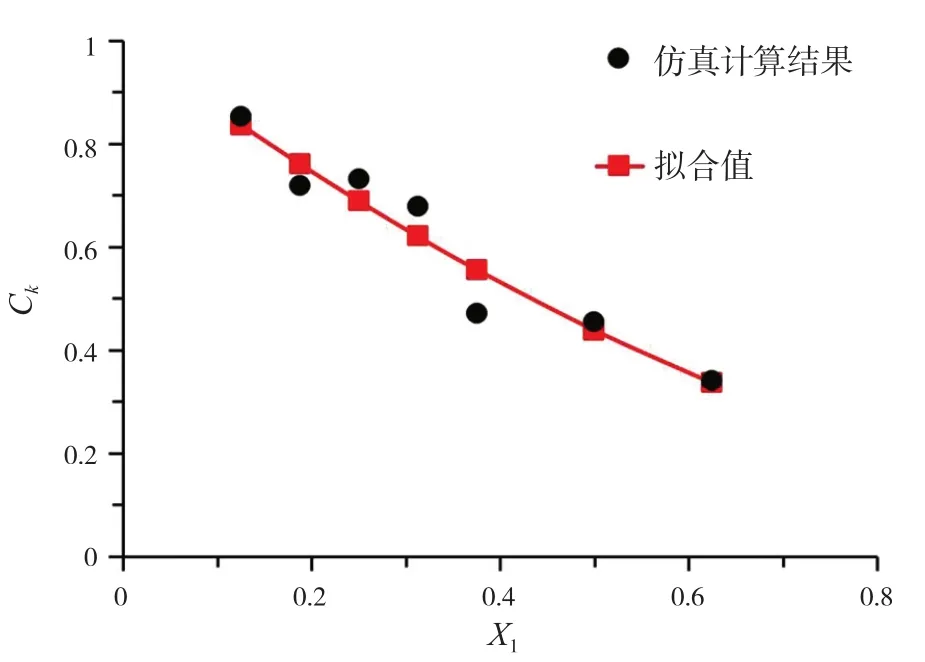
图13 开口效应因子Ck回归公式对比
(1)对比二维、三维平底结构砰击压力的计算结果,发现三维平底结构入水砰击时,由于流体的流动具有三维特性,会增强空气垫的作和,使得砰击面上砰击压力峰值变小11%左右;设计砰击压力的规范值考虑到船体砰击压力具有瞬时性、空间分布的特点,对平底结构砰击压力峰值进行较大幅度的折减。
(2)对比开口结构与不开口结构砰击压力的计算结果,发现底部开口会使平底结构砰击压力变小,且随着开口尺寸的增大,开口对平底结构砰击压力分布的影响也越大,砰击面处砰击压力均值沿横向会减少30%~70%左右,沿纵向会减少14%~30%左右。
(3)提出了船底开口结构砰击压力峰值折减因子,可和于体现开口对砰击压力的影响。

