基于多尺度跳跃深度长短期记忆网络的短期多变量负荷预测
肖 勇,郑楷洪,郑镇境,钱 斌,李 森,马千里*
(1.南方电网科学研究院有限责任公司,广州 510080;2.华南理工大学计算机科学与工程学院,广州 510006)
0 引言
随着社会经济的发展和人民生活水平的提高,对供电质量提出了更高的要求。精确的电力负荷预测能为电量生产和供电调度提供可靠的指导,从而提升电力系统的供电质量。
传统的电力负荷预测方法有时间序列分析[1]、回归分析[2]和卡尔曼滤波[3]等。随着人工智能技术的发展,神经网络[4-5]、支持向量回归[6]和高斯过程[7]等智能方法被应用于电力负荷预测,其中神经网络拥有较强的非线性拟合和自学习能力,能够较好地解决传统方法非线性拟合能力差的缺陷。循环神经网络(Recurrent Neural Network,RNN)[8]是一类拥有循环连接的神经网络,能够对时序数据进行建模。因此,在人工智能方法中使用RNN 为主体构建的预测模型成为短期电力负荷预测模型的典型代表。虽然RNN 具有时序建模的能力,但存在“梯度消失”和“梯度爆炸”的问题。为了解决该问题,Hochreiter 等[9]提出了长短期记忆(Long Short-Term Memory,LSTM)网络。文献[10]和文献[11]成功将LSTM 应用到短期电力负荷预测中,提升了负荷预测精度。然而,短期电力负荷数据中存在着多尺度时序特征,其具体表现为在年、月、星期和日不同期限上均具有明显的周期性[12]。近年来,在时间序列分类[13]和聚类[14]任务中,多尺度特征已经展示出能有效提升模型性能的潜力。然而,如何高效地对存在于短期电力负荷数据中的多尺度时间结构进行建模,进一步提升短期电力负荷预测的精度,仍未得到广泛的研究。
针对电力负荷数据中存在的多尺度时间结构,本文提出了一种基于多尺度跳跃深度LSTM(Multi-scale Skip Deep Long Short-Term Memory,MSD-LSTM)的短期电力负荷预测模型。该模型使用多层LSTM 网络架构并且每层设计不同的跳跃连接。LSTM能够较好地对电力负荷进行建模,跳跃连接使得模型具有捕获负荷数据中多尺度时序特征的能力。实验结果证明该模型有效地提升了短期电力负荷预测的精度。
本文的主要贡献如下:
1)提出了一种基于多尺度跳跃深度LSTM 的短期电力负荷预测模型,通过使用不同的跳跃连接来捕获短期电力负荷数据中的多尺度时序结构特征,帮助模型更好地进行负荷预测;
2)两个地区负荷数据的实验结果表明所提出的短期负荷预测方法可以有效提高电力负荷预测精度。
1 时间序列分析
电力负荷数据从长期来看是波动变化的,但是这种波动变化会呈现出周期性和连续性的特点。对于短期电力负荷预测而言,其在年、月、星期、日不同期限上均具有明显的周期性。
图1 所示为某地区四个星期的电力负荷变化曲线。从图1 可以看出,每个星期中工作日的负荷值较为平稳,此时工业和商业用电主导。在休息日,负荷从工业和商业用电主导转变为家庭用电主导,负荷值呈现下降趋势。此外,从图1 中可以看出电力负荷值在星期这个时间尺度上呈现出明显的周期性。
通过上述分析可以发现,时间是短期电力负荷预测中重要的影响因素,这使得电力负荷数据呈现出规律波动的特点并具有明显的周期性。针对短期电力负荷数据存在的周期性变化,本文利用多层LSTM 并且在每层设置不同的跳跃连接数,显式地建模电力负荷数据中存在的多尺度时间结构,从而更好地进行短期电力负荷预测。

图1 某地区四周的负荷变化曲线Fig.1 Four-week load curve of an area
2 LSTM
虽然RNN 具有时序建模的能力,能够较好地应用于电力负荷预测任务,但在误差反向传播时,会存在“梯度消失”和“梯度爆炸”的问题。为了解决RNN 存在的问题,Hochreiter等[9]提出了LSTM。LSTM 通过专门地设计隐含层单元来解决长期依赖问题。不同于标准的RNN,LSTM 在隐含层的内部设计了遗忘门、输入门、输出门以及细胞状态,这使得LSTM能够拥有良好的长短期记忆能力。
LSTM的隐含层单元可以看作一个细胞,细胞状态保存了长期记忆。细胞状态在每个时刻与当前输入进行少量的线性交互,从而允许网络在较长持续时间内保存信息。此外,当信息被使用,网络可以遗忘旧的状态。
LSTM 的隐含层内部结构如图2 所示,其中xt表示t时刻LSTM 输入变量,ht和ht-1分别表示t和t-1 时刻的隐含层状态,Ct和Ct-1分别表示t和t-1时刻的细胞状态,ft表示遗忘门的输出,it表示输入门的输出,C~t表示t时刻用来更新细胞状态的备选信息,ot表示输出门的输出,σ表示sigmoid函数。
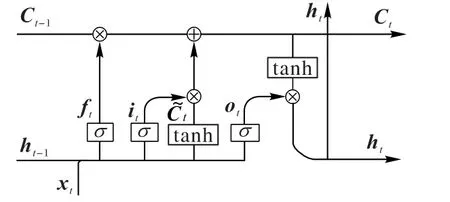
图2 LSTM隐含层内部结构Fig.2 Hidden layer internal structure of LSTM
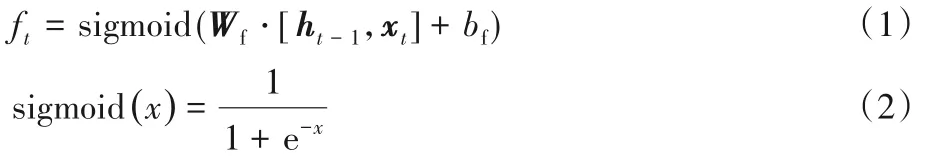
式(1)中:Wf表示遗忘门权重矩阵,bf表示遗忘门偏置。根据式(1)和式(2)可知,ft为一个0 到1 的实数,这决定了细胞状态的遗忘比例。
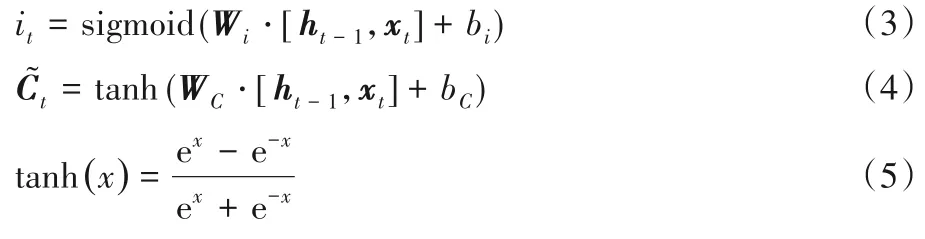
同样的,式中的Wi和WC表示连接权重矩阵,bi和bC表示偏置。it为0到1的实数表示t时刻用来更新细胞状态的备选信息,tanh(·)表示双曲正切函数。
在遗忘门中细胞状态与ft相乘,遗忘需要丢弃的信息;在输入门中再加上更新细胞状态。这可以用以下公式表示:

最后,LSTM 需要确定输出什么值,这个输出是基于经过更新的细胞状态,具体过程可以用以下公式表示:
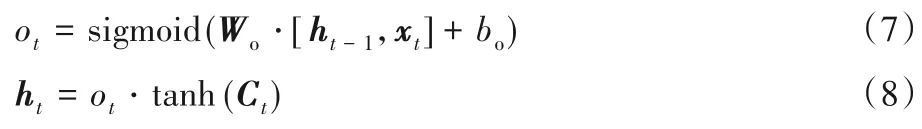
其中:Wo表示输出门权重矩阵,bo表示输出门偏置。简便起见,本文将LSTM 隐含层状态的更新过程表示为函数FLSTM(·),在长短期记忆网络的前向传播过程中,隐含层状态的更新公式为:

3 基于MSD-LSTM的负荷预测模型
3.1 MSD-LSTM
LSTM 虽然有效地解决了RNN 存在的无法有效学习长时依赖的问题,但是电力负荷数据中存在着不同尺度的时间结构特征,而LSTM 却不具备捕捉多尺度时间特征的能力。针对该问题,本文对LSTM 进行改进,提出了一种基于多尺度跳跃深度长短期记忆(MSD-LSTM)网络的短期负荷预测方法,使其具有捕捉电力负荷数据中多尺度时序信息的能力。MSD-LSTM 通过把LSTM 的拓扑结构设计为多层并且加入循环跳跃连接[15],以此改变历史信息与当前信息的交互周期,使得每层拥有了不同时间周期的建模能力,显式地对电力负荷数据中的多尺度时间结构进行建模。MSD-LSTM 的每一层使用不同循环跳跃尺度的LSTM,即每个时刻的隐含层状态更新时依赖的不是上一个时刻的隐含层状态,而是依赖多个时刻之前的状态。如图3 所示,第一层的跳跃连接数为1,则第一层为传统的LSTM;第二层的跳跃连接数为2,则隐含层状态更新时依赖的是往前两个时刻的隐含层状态;第三层的跳跃连接数为4,则隐含层状态更新时依赖的是往前4个时刻的隐含层状态。加入循环跳跃连接后的LSTM 的更新过程可以表示为:

其中上标i表示层数,后续模型部分的所有上标皆为该含义。
在网络训练的前向传播过程中,第一层LSTM 的输入为预处理后的电力负荷数据以及天气数据组成的多维变量序列,如图3 中输入数据为1 到T时刻的负荷数据,维度为T×D,T表示输入的时刻数,D表示每个时刻输入的向量的维度;输出为T+1时刻的负荷预测值。天气数据帮助模型更好地进行负荷预测。其余层的输入为上一层LSTM 的输出,最后把每一层最后一个时刻的隐含层状态进行拼接后输入到全连接层形成融合特征,利用该融合特征进行未来负荷值的预测。多层不同跳跃尺度的LSTM 前向传播过程可以用下列公式表示:
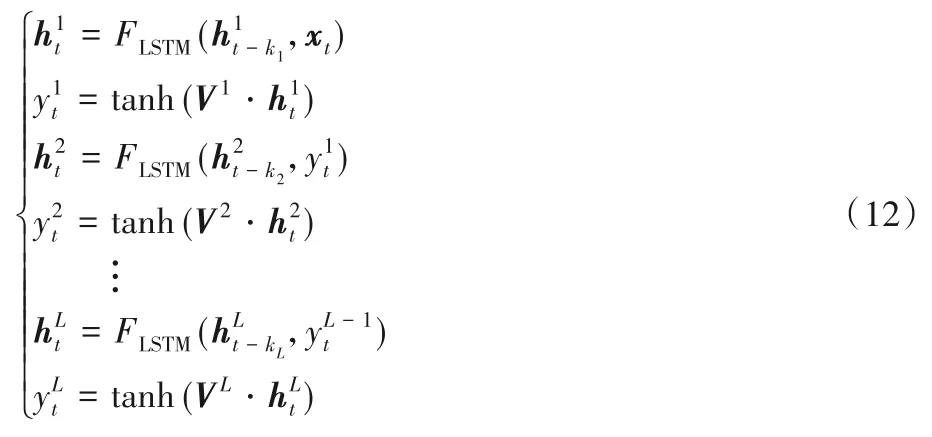
MSD-LSTM的网络结构如图3所示,其中方框内的圆形表示图2的LSTM 单元,圆形左边的箭头表示接收上一个时刻的隐含层状态;右边的箭头当前时刻的隐含层状态输入到下一个时刻的LSTM 单元;下方的箭头表示当前时刻的输入;上方的箭头表示当前时刻的LSTM 单元的输出。使用前T个时刻的数据来预测T+1 时刻的负荷值,每个时刻的输入为一个6维向量,即D为6,包含负荷数据以及天气数据。网络层数设为3 层,每一层的跳跃连接数分别为1,2 和4。最后,通过全连接层将每层LSTM 第T个时刻的隐含层状态进行融合得到融合特征,利用该融合特征去预测下一时刻的负荷值。
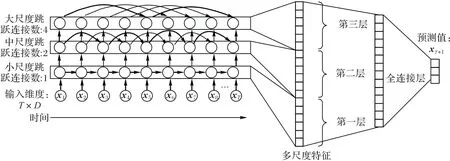
图3 MSD-LSTM网络结构Fig.3 Structure of MSD-LSTM network
MSD-LSTM 通过给每层LSTM 设计不同的跳跃连接数,使得每层拥有不同时间周期的建模能力。本文研究的负荷预测是短期电力负荷预测,其在年、月、星期、日不同期限上均具有明显的周期性。因此,MSD-LSTM 第一层的跳跃连接数设为1,捕捉日依赖关系;第二层的跳跃连接数设为7,捕捉周依赖关系;第三层的跳跃连接数设为30,捕捉月依赖关系。最后通过引入全连接层,把每层提取到的不同尺度信息进行融合,即将每层T时刻的隐含层状态拼接后作为全连接层的输入,实现多尺度结构信息的融合,并把全连接层的输出作为预测值,即T+1时刻的负荷值。全连接层可以使用以下公式表示:

其中:Wfc为全连接层权重,b表示偏置,xT+1为全连接层的输出,HT为各层LSTM 最后一个时刻隐含层状态的拼接,可以用以下公式表示:
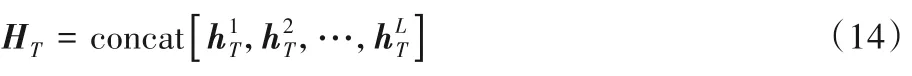
3.2 基于MSD-LSTM的短期负荷预测算法流程
步骤1 构建时间序列数据进行训练和测试。对电力负荷数据以及天气数据进行归一化,采取一步预测的方法并对归一化后的数据做窗口滑动处理得到N条长度为T的负荷序列样本集,即以前T个时间点的数据作为“特征”,下一个时间点的数据作为“标签”。将样本集按7∶3 的比例划分为训练集和测试集,即前0.7×N条序列作为训练集,后0.3×N条序列作为测试集。
步骤2 逐层构建LSTM,每一层设置不同的跳跃连接以建模多尺度时序依赖关系。
步骤3 构建全连接层将各层LSTM 的依赖关系进行融合并把全连接层的输出作为预测值形成多尺度跳跃深度LSTM模型。
步骤4 训练步骤3构建的模型,在网络训练的前向传播过程中,第一层LSTM 输入为经步骤1 处理过的训练数据集,其余层的输入为上一层LSTM 的输出,把每一层最后一个时刻的隐含层状态进行拼接后输入到全连接层形成融合特征,利用该融合特征进行未来负荷值的预测。在网络训练的反向传播过程中,使用基于时间的反向传播(BackPropagation Through Time,BPTT)算法[16]来最小化损失函数,即均方误差,从而优化模型的参数。
步骤5 使用训练后的模型对经步骤1 处理过的电力负荷测试数据集进行预测,计算预测值和真实值之间的均方误差。
4 实验分析与比较
4.1 数据来源
本文研究的是带有天气数据的短期电力负荷预测,使用2012年1月1日到2014年12月31日两个地区真实负荷数据,数据来源于2016 年电工数学建模竞赛A 题。此外,这个数据集还提供最高温度、最低温度、平均温度、相对湿度和降雨量5个天气数据。本文利用这5个天气数据来帮助负荷预测,即将负荷数据以及5个天气数据拼接为6维向量。
本文分别抽取两个地区每天6:00、12:00和18:00的负荷值进行负荷预测,因此总的样本集有6 个,每个样本集中有1 096 个时间点,每个时间点为一个6 维的向量,包含负荷及天气数据。负荷和天气数据拥有不同的数量级和量纲。为了去除这些影响,需要对输入量进行归一化处理,将其转化为无量纲的纯数值。本文采取离差标准化的归一化方式。每个样本集原始数据表示为s=[s1,s2,…,sn]T其中sj=对原始数据进行如下归一化:
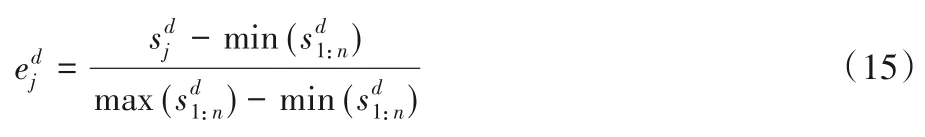
得到归一化的样本集e=[e1,e2,…,en]T。
4.2 实验设置
这部分展示了MSD-LSTM 应用在短期电力负荷预测上的实验设置。本文将MSD-LSTM 与多层长短期记忆(Multi-layer Long Short-Term Memory,MLSTM)网络、单层长短期记忆(Single-layer Long Short-Term Memory,SLSTM)网络、支持向量回归(Support Vector Regression,SVR)[17]和高斯过程(Gaussian Process,GP)[18]进行了对比实验。使用过去35 天的负荷值和天气数据来预测下一天的负荷值,则对样本集做窗口滑动处理得到1 062 条长度为35 的序列,即样本。构建时间序列数据进行训练和测试时,将1 062 个样本集按7∶3 的比例划分为训练集和测试集。MSD-LSTM 的层数设为3,每层的跳跃尺度分别设为1、7、30,相应的每层分别对时间尺度以天、周、月为单位的电力负荷数据时序依赖关系进行捕捉。为了检验MSD-LSTM 对电力负荷数据中的多尺度时间结构的捕捉能力,本文设置了MLSTM 和SLSTM 两个对比实验。MLSTM 的层数设为3,每一层的跳跃尺度设为1,以检验多尺度时间结构对预测性能的提升;SLSTM 的层数设为1,跳跃尺度设为1,以检验深层网络结构对预测性能的提升。LSTM 的隐含层单元数固定为48。为了保证对比实验的公平,本文保持上述三种模型在每个样本集上所使用的隐含层单元数一致。SVR 和GP 同样使用过去35 天的负荷值和天气数据来预测下一天的负荷值。每天的数据包含负荷值以及5 个天气数据,因此本文将35天的数据拼接成一个35×6的向量作为模型的输入,并预测下一天的负荷值。此外,SVR 和GP 都是基于核函数的模型,在本文中SVR 和GP 的核函数都选取高斯核函数。
MSD-LSTM、MLSTM 和SLSTM 训练时使用mini-batch 技术,batch size 设置为32,即训练时每次迭代输入32 个样本并计算损失函数,根据损失函数反向传播更新网络的参数。训练时使用mini-batch 技术,可以使网络参数更新更快,同时有利于网络参数更加鲁棒地收敛。此外,为了防止过拟合,在全连接层使用Dropout,Dropout率设为0.05。
4.3 实验结果
4.3.1 对比实验
使用MSD-LSTM 与MLSTM、SLSTM、SVR 和GP 分别进行实验并对比。表1 为各模型在短期电力负荷上的预测结果,采用均方误差(Mean Squared Error,MSE)作为评判标准:

其中:yi和分别表示测试集中对应第i个样本的真实值和预测值,M表示测试集样本个数。
从表1 可以看出,MSD-LSTM 在6 个样本集中的短期负荷预测都取得了较好的预测精度。一方面,与SVR 和GP 对比,MSD-LSTM 是以LSTM 为主体构建的预测模型,能够较好地处理序列建模任务,而SVR和GP并未对存在于电力负荷数据中的时序依赖关系进行建模,因此MSD-LSTM 的预测性能要明显优于这两种方法;另一方面,与SLSTM 对比,MSD-LSTM 由三层LSTM 构成,能够更好地建模电力负荷数据中的动态特性,取得了更好的预测精度,表明深层网络结构有利于预测性能的提升。与MLSTM 对比,MSD-LSTM 通过循环跳跃连接对短期电力负荷中的日、周和月的时序依赖关系进行建模,增强了LSTM 对多尺度时序结构建模的能力,取得了更好的预测精度,表明多尺度时间结构能够提升预测性能。因此,MSDLSTM 通过结合深层网络结构建模动态特性的能力以及多尺度跳跃连接提取多尺度时间结构信息的能力,有效地提升了短期电力负荷预测精度。
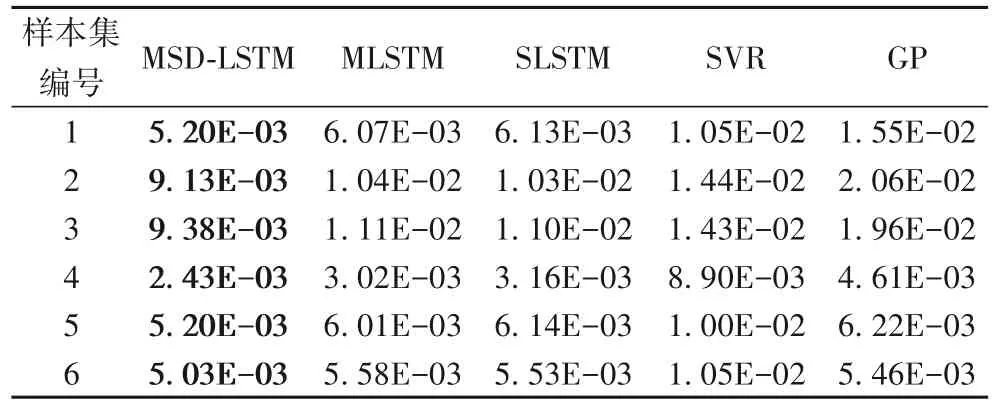
表1 不同方法的负荷预测均方误差(MSE)对比Tab.1 Comparison of load forecasting MSE of different methods
更进一步地,本文从6 个样本集中随机抽取1 个样本集,使用上述各种模型对其进行负荷预测,并对比了各种模型的绝对误差。绝对误差越接近0说明预测精度越高,越远离0说明预测精度越低。图4 展示了MSD-LSTM、SLSTM、MLSTM、SVR 和GP 五种模型预测的负荷值与实际负荷值的绝对误差曲线。对比5 条绝对误差曲线,可以看出MSD-LSTM 能够取得最好的预测精度,具体表现为取得了最低的绝对误差,平均值为0.069。
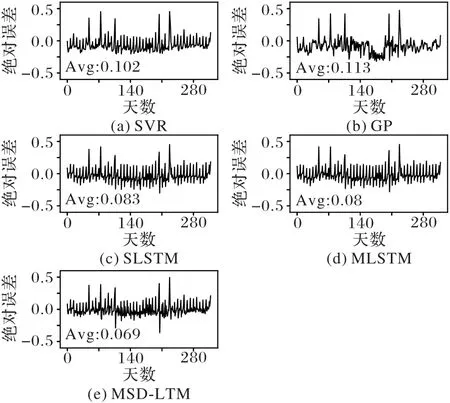
图4 不同方法的绝对误差曲线Fig.4 Absolute error curves of different methods
4.3.2 超参数探究
为了探究层数、跳跃数以及步长(即使用过去多少天的数据来进行下一天的负荷预测)对MSD-LSTM 性能的影响,本文设置了7组使用不同超参数的对比实验,其在6个样本集上的结果如表2所示。首先,对比实验1和实验4的结果,实验4取得了更低的MSE,这表明深层网络有利于提升短期负荷预测的精度。对比实验2 和实验7 可以得到同样的结果。进一步的,对比实验4,5 和7 的结果,实验7 取得了最低的MSE。这表明跳跃数会影响模型的性能,同时根据数据实际的多尺度时间结构来选择合适的跳跃数有利于提升模型的性能。最后,对比实验2,3 以及实验6,7 的结果,可以发现具有更短步长的模型可以取得更好的结果。因此,有效地使用MSDLSTM需要综合考虑多个超参数的影响。
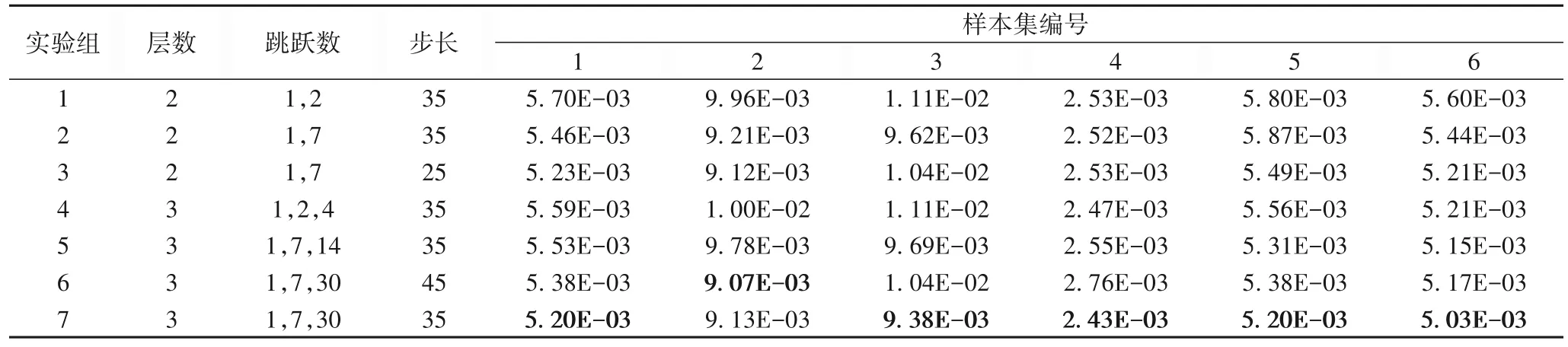
表2 不同超参数设置的负荷预测均方误差(MSE)对比Tab.2 Comparison of load forecasting MSE of different hyperparameter settings
5 结语
本文针对LSTM 无法有效建模电力负荷数据中存在的多尺度时间结构的问题,提出了MSD-LSTM。MSD-LSTM 将LSTM 的拓扑结构设计为多层并在每层中设置不同的跳跃连接,显式地对短期电力负荷数据中的多尺度时间结构进行建模。通过两个地区负荷数据的实验分析,证明了MSD-LSTM能够有效地捕捉短期电力负荷数据中的多尺度时间结构,从而提升负荷预测精度。
MSD-LSTM 采取的跳跃连接数是手工设置的,需要依靠先验知识,无法自适应地学习电力负荷数据的多尺度结构。未来的工作会研究如何动态自适应地学习跳跃连接,更好地根据电力负荷数据来学习多尺度结构并对其进行建模,进一步提高电力负荷预测的精度。

