图趋势过滤诱导的噪声容错多标记学习模型

林腾涛，查思明，陈 蕾，2*，龙显忠

（1.南京邮电大学计算机学院、软件学院、网络安全学院，南京 210003；2.江苏省大数据安全与智能处理重点实验室（南京邮电大学），南京 210003）

0 引言

在现实生活中，一个示例通常与多个标记相关联，例如，一篇文档可能与多个不同主题相关，一幅图片通常包含多个物体，一段音乐可能有多个体裁。因此，多标记学习受到了广泛的关注，并在文本分类、图像标注、图像分割、动作识别、面部表情识别、生物信息学等各个领域都取得了成功应用。

多标记学习旨在从一系列候选标记集中选出与样本相关的标记，由于标记集有着大量的标记并且多个标记在某个语义空间里通常是相互关联的，因此，探索标记之间的关联关系有助于多标记学习。例如，在图像标注中，如果标记“骆驼”和“仙人掌”同时出现，那么有极大可能性会出现“沙漠”这个标记，而出现“蝴蝶”这一标记的可能性就极低。多标记学习试图将不同程度的标记相关性结合起来，已有许多相关算法被提出来探索标记之间的关联关系。其中，标记排序方法通过考虑两两标记之间的关系从而将多标记分类问题转化为标记排序问题［1-2］。进一步地，为了探索标记之间的高阶关联关系，即一个标记与其他所有标记之间的关联关系，最典型的方法是将原始标记向量投影到一个低维的标记空间中［3］，文献［4］同时考虑了全局和局部的标记关联关系，文献［5］将原始离散的二值标记空间扩展成欧氏空间，并同时考虑了特征流形和标记流形结构。

然而在许多实际应用中，获得的数据往往是不完美的，往往同时包含特征噪声和标记噪声，忽略任意一种噪声都将影响多标记学习模型的预测性能，而现有的多标记模型大多只考虑其中一种噪声。一方面，标记可能会有缺失或者错误，针对标记噪声，通过标记之间的关联关系可以很好地解决标记缺失［6］，文献［7-8］利用直推式半监督学习方法补全缺失标记，文献［9］试图解决基于标记缺失的大规模多标记学习问题。另一方面，特征也可能存在噪声，例如图片模糊等，针对特征噪声，文献［10-11］提出许多方法解决特征噪声。尽管文献［12］解决了特征噪声和标记噪声同时出现的情况，但是基于L2范数诱导的图拉普拉斯正则化在含噪的数据集中可能并不准确，忽略了含噪特征向量与标记向量的不一致性，即噪声容错性不足。

为了解决上述问题，本文提出了一种图趋势过滤诱导的噪声容错多标记学习（Graph trend filtering guided Noise Tolerant Multi-label Learning，GNTML）模型。该模型通过采用组稀疏约束桥接标记增强矩阵的机制来同时容忍特征噪声和标记噪声。具体地，本模型通过探索标记之间的内在关联关系学习得到一个标记增强矩阵，用增强过后的标记矩阵替代原始标记矩阵，以解决可能存在的标记缺失，这个标记增强矩阵理想情况下是根据特征矩阵获得的，进一步，为了在混合噪声场景下学习到合理的标记增强矩阵，本文一方面引入图趋势过滤（Graph Trend Filtering，GTF）［13］机制来容忍含噪示例特征与标记之间关联的不一致性，即某些示例由于存在噪声特征相似，但实际上它们的标记却是不相近的。另一方面，本文引入组稀疏约束的标记保真惩罚来减轻标记噪声对标记增强矩阵学习的影响，以及组稀疏约束同时解决特征噪声。此外，本文还通过引入标记关联矩阵的稀疏约束来刻画标记之间的局部关联特性，使得样本标记能够在相似样本之间得以更好的传播。本文利用交替方向法（Alternating Direction Method，ADM）来有效地求解模型，并在7 个真实多标记数据集上的实验表明，本文提出的噪声容错多标记学习模型在66.67%的情况下取得最优值或次优值，能有效地提高多标记学习的鲁棒性。

1 相关工作

基于标记之间的关联程度，多标记学习问题求解策略通常可以被划分为三种［14］：最简单的一种是“一阶”策略，该策略逐一考察单个标记而忽略标记之间的关联关系，最典型的算法就是BR（Binary Relevance）［15］，将多标记问题转化为多个二分类问题，为每一个标记都训练一个分类器；相应地，“二阶”策略考察两两标记之间的相关性，从而构造多标记学习系统，例如校准标记排序（Calibrated Label Ranking，CLR）［2］，将多标记问题转化问为两两标记之间的排序问题，然而当实际问题中标记具有超越二阶的相关性时，该策略会受到影响。“高阶”策略则考察了高阶的标记相关性，考虑了所有标记之间的关联关系，例如CC（Classifier Chain）［16］，将多标记问题转化为链式的二元分类问题，虽然“高阶”策略可以较好反映真实世界问题的标记相关性，但通常模型复杂度较高，计算代价太大。文献［5］则把标注信息标记当作训练样本示例的丰富语义化编码的简化。

然而，获得的数据集通常并不是完美的，往往含有各种噪声，因此，含噪多标记学习取得了很大关注。通常噪声包含两方面：特征噪声和标记噪声。针对标记噪声，由于多标记学习有着大量类标记，在某些实际应用中可能只能观察到部分标记，且多标记学习性能受不完整标记影响很大，对此提出了许多减少性能衰退的方法。例如：文献［17］提出了一种基于正则化的归纳式半监督多标记学习方法；文献［18］通过考虑标记关联来恢复完整的标记矩阵；文献［19］首先选出关键标记，再根据标记进行排序，然后利用组稀疏，最后采用支持向量机（Support Vector Machine，SVM），从而处理标记缺失；文献［20］是基于矩阵补全的多视图弱监督学习来解决标记噪声；文献［4］通过建模全局和局部标记关联性，学习潜在标记表示并优化标记流形来解决标记缺失。针对特征噪声，文献［21］通过降维，文献［22］通过特征选择来解决特征噪声。文献［12］同时解决了特征噪声和标记噪声。

2 模型框架

2.1 预备知识

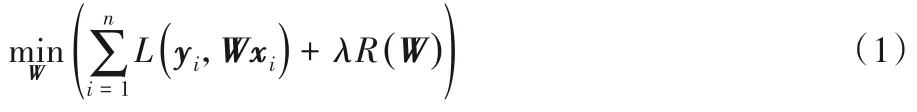
其中L(·，·)和R(·)分别表示损失函数和关于W的正则化项。W根据不同的前提假设设计不同的正则化项。

2.2 图趋势过滤诱导的噪声容错多标记学习模型

本文所提出的图趋势过滤诱导的噪声容错多标记学习模型GNTML 是针对特征噪声和标记噪声共同出现的场景。具体来说，首先在含有噪声的训练集中探索不同标记之间的关联关系，以此获得一个新的标记增强矩阵，这个增强的标记矩阵理想情况下是根据特征矩阵获得的。但是由于数据集是含有噪声的，因此借助图趋势过滤的噪声容错能力来容忍含噪示例特征与标记之间关联的不一致性，从而减轻特征噪声对标记增强矩阵的影响。接着用这个标记增强矩阵代替原始标记矩阵，引入组稀疏同时解决特征噪声和标记噪声，从而学习从特征空间到增强标记空间的映射，所提模型整体框架如图1所示。

为了得到这个标记增强矩阵，该模型在含噪的训练集中学习得到一个标记关联矩阵B∈Rc×c，其中bij表示标记yi与标记yj的关联程度，基于新的标记增强矩阵，学习得到的预测模型W由于考虑到特征和标记的关联关系将变得更加合理。目标函数如下：

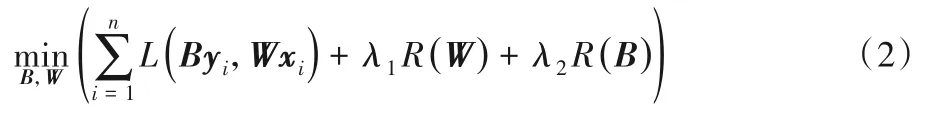
其中R(B)表示关于B的正则化项。可以观察到，通过自适应学习得到的投影矩阵B可以捕获所有c个不同标记之间的关联关系，例如，大多数样本同时出现“蓝天”和“白云”两个标记，那么这两个标记是强关联的，则在投影矩阵B中可以体现，并且这是个一对多的高阶依赖关系BY，而不是一对一的依赖关系。这样一来，就可以通过其他标记之间的关联关系来重构任何丢失的标记，矩阵就是标记增强矩阵。此外，获得的标记增强矩阵应该与原始标记矩阵保持一致性，因此本文定义了一个标记保真惩罚项来刻画原始标记矩阵与标记增强矩阵之间的差异。考虑到标记噪声的存在，同时施加了组稀疏约束，标记保真惩罚项定义如下：

其中，关于一个A∈Rp×q矩阵的L2，1范数定义为‖A‖2，1=

回忆一下，该模型目的是在特征噪声和标记噪声共现时学习标记增强矩阵，由于GTF 是一种对图进行非参数回归的统计方法，通过L0惩罚图顶点之间标记差取代通常用的L2范数的图拉普拉斯平滑假设，有着很强大的噪声容错能力和局部自适应性。因此本文引入GTF来更好诱导标记增强矩阵的学习。首先基于训练样本构建一个邻接矩阵S，sij刻画了示例i和示例j的特征相似度，如果示例j属于示例i的k个最近邻样本集，则它们的相似度通过如下高斯核函数计算，否则sij=0：

其中δ表示高斯核宽度。接着用邻接矩阵S来构造一个图G(V，E)，V={xi|1 ≤i≤n}表示训练样本组成的顶点集合，E={(xi，xj)|sij≠0，1 ≤i≠j≤n}表示边的集合，如果sij非0，则表示示例i与示例j有边相连。

此外，本文又定义一个n×e的矩阵P，其中e表示图G中边的条数，若第k条边连接xi和xj，则矩阵P的第k列定义如下：

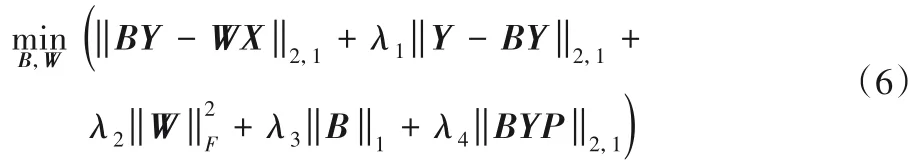
值得注意的是，考虑到部分标记之间可能没有关联关系，因此这里给B施加一个L1范数约束，学习得到一个稀疏的标记关联矩阵。同时通过组稀疏‖BY-WX‖2，1处理有损坏的特征，如图1 中的图片c，利用组稀疏使得对特征噪声更加鲁棒。

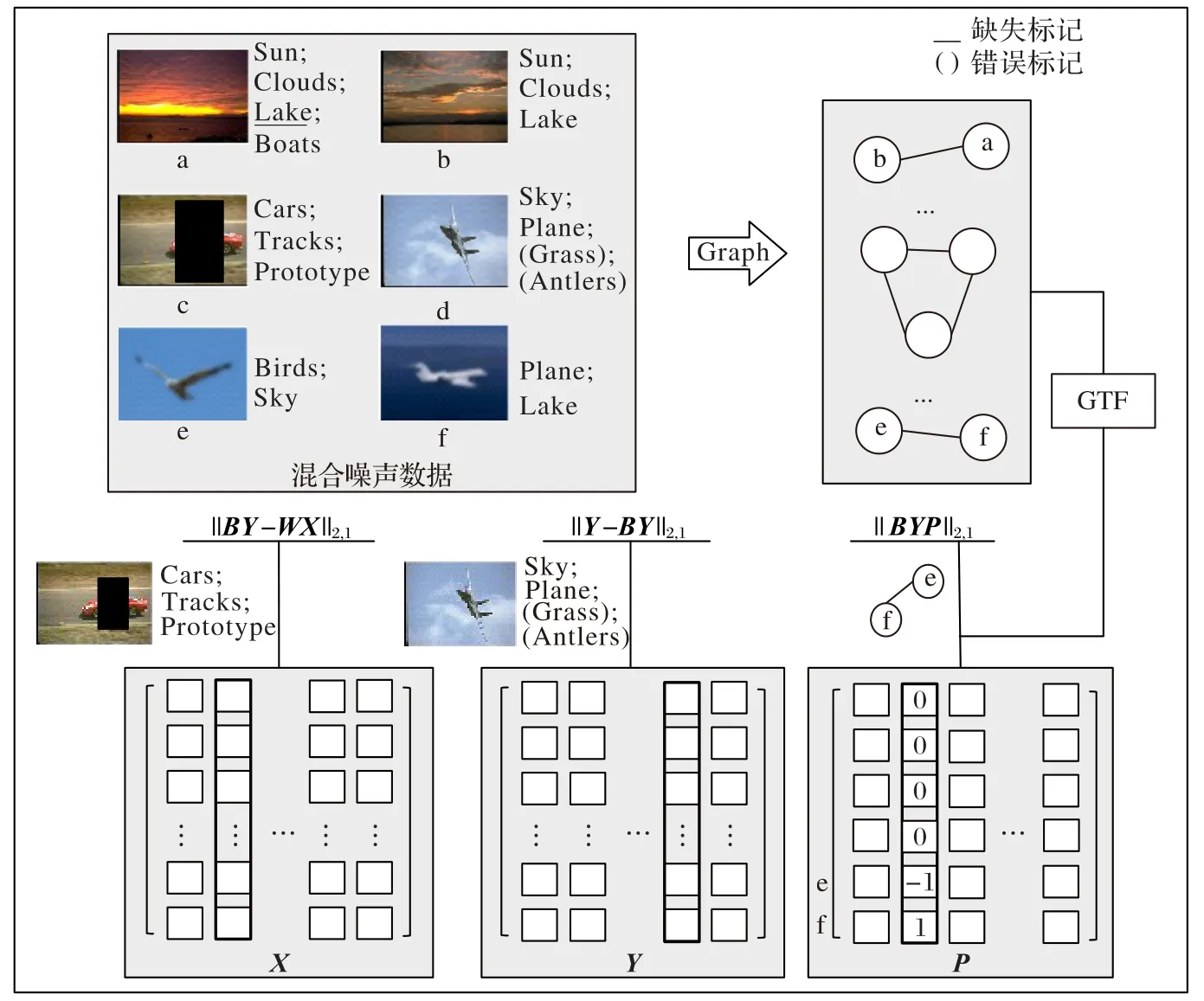
图1 模型框架Fig.1 Model framework

本文所提模型有如下优势：1）利用标记增强矩阵BY代替原始标记矩阵Y以解决标记的缺失；2）本文通过组稀疏同时处理特征噪声和标记噪声；3）在GTF 的诱导下探索了数据的局部特性，即特征相似的样本标记也相近，保留了原始特征空间的局部几何结构，并过滤掉那些由于特征噪声存在使得特征相似但实际上标记却不相近的样本。

3 优化求解

因为式（6）是凸的，因此解决的方法有很多，本文采用交替方向法（Alternating Direction Method，ADM）求解，但是由于L1范数项是非平滑的，因此为了求解方便，引入辅助变量C，令B=C，从而式（6）等价变为：

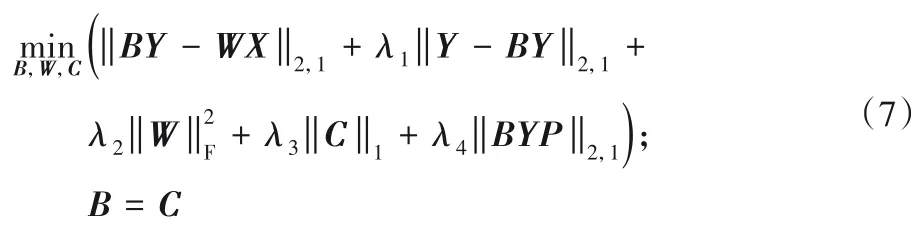
对应的增广拉格朗日函数如下：

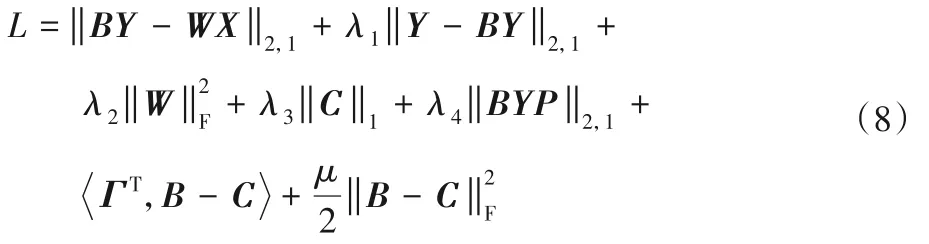
由于上述问题是无约束的，因此可以通过固定其他变量来分别优化B、W和C，然后更新乘子Γ，其中μ＞0 是惩罚系数。

固定W和C，更新B：

当固定W和C，关于B优化问题变为：

可以写成如下关于B的函数形式：

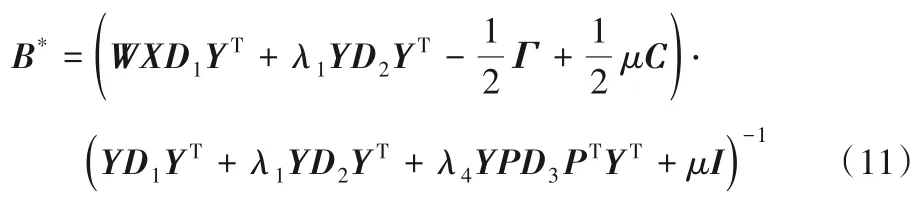
固定B和C，更新W：

当固定B和C，关于W的函数变为：

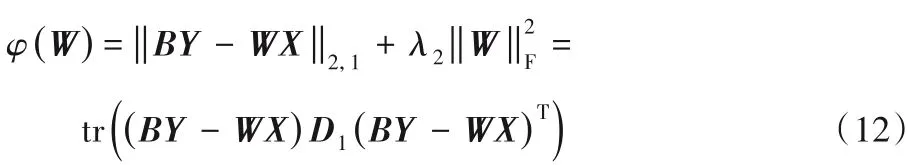
令上述关于W的函数导数为0，可得

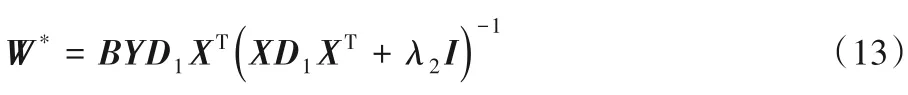
固定B和W，更新C：

当固定B和W，关于C优化问题变为：

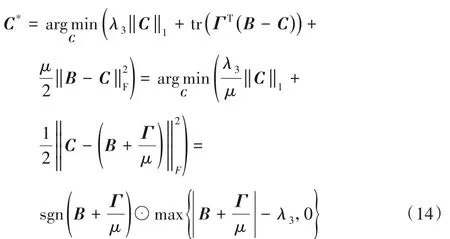
其中：⊙表示哈达玛积，sgn(·)表示signum函数。

更新乘子Γ：

算法1给出了该优化算法框架的伪代码。

算法1 所提出的GNTML模型的优化算法。

输入：训练样本特征矩阵X∈Rd×n，标记矩阵Y∈Rc×n，以及超参数λ1，λ2，λ3，λ4；

输出：线性分类器W，标记关联矩阵B。

4 实验

4.1 数据集和评价指标

为了证明所提方法的有效性，本文在7 个标准多标记数据集上进行了实验：Birds、Emotion、CAL500、Scene、Corel5k、Medical、Genbase。这些数据集均来自Mulan 网站（http：//mulan.sourceforge.net/datasets-mlc.html）。数据集的详细信息如表1 所示，注意这里的LCard（label cardinality）是一种多标记标记密度的量，是用来指示在数据集中每一个样本平均有多少个标记。

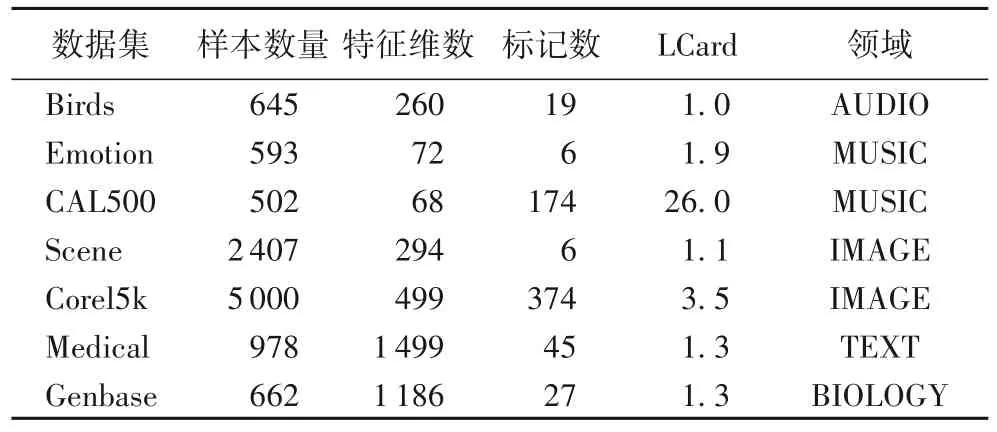
表1 多标记数据集的特征Tab.1 Characteristics of multi-label datasets

与文献［23］的工作类似，本文采取了5 种常见的评价指标。给定一个多标记测试集，其中Yi为隶属于示例xi的相关标记集合，以及h(xi)表示示例i的预测标记集合，f(xi，y)对应xi具有标记y的“置信度”。此外，实值函数f(·，·)还可以转化为一个排序函数

Hamming Loss（HL） 用于考察样本在单个标记上的误分类情况，例如一个相关标记未出现在预测的标记集合中或者无关标记出现在预测的标记集合中。

其中Δ用于度量两个集合之间的“对称差”。

Ranking Loss（RL） 用于考察在样本的类别标记排序序列中出现排序错误的情况，即不相关标记在排序序列中位于相关标记之前。

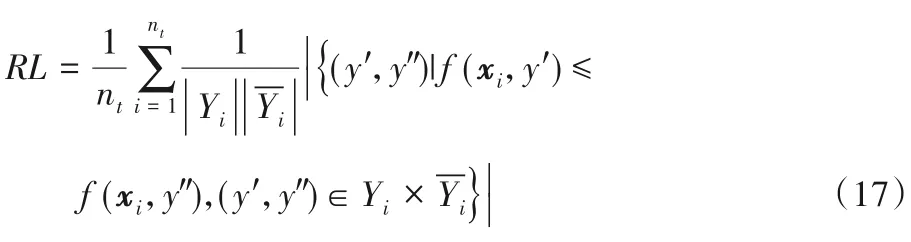
One Error（OE） 用于考察在样本的类别标记排序序列中，序列最前端的标记不在相关标记集合中的比例。

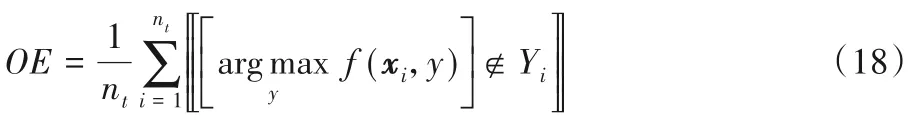
Coverage（Cov） 用于考察在样本的类别标记排序序列中，覆盖所有相关标记所需的搜索深度情况。

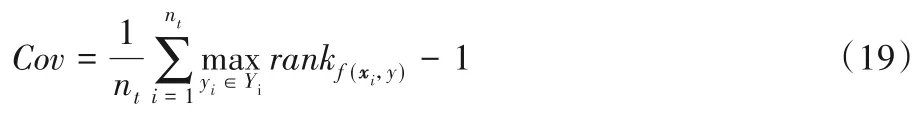
Average Precision（AP） 用于考察样本的类别排序序列中，排在相关标记之前仍为相关标记的情况。

上述这些评价指标常用于多标记学习中，并且可以从不同角度评估多标记算法的性能。对于Average Precision，值越大，分类器的性能越好，对于其他值，值越小分类器的性能越好。

4.2 实验设置

本文将所提模型同几个相关的算法进行比较，包括文献［15］提出的BR（Binary Relevance），BR 将多标记学习问题转化为多个“二分类”问题求解；文献［23］提出的基于k近邻（k-Nearest Neighbor，kNN）的多标记学习算法ML-kNN（Multilabel Learning-k-Nearest Neighbor），ML-kNN 将“惰性学习”算法k近邻进行改造以适应多标记学习；文献［2］提出的校准标记排序（Calibrate Label Ranking，CLR），CLR 通过“成对比较”将多标记学习转化为标记排序问题，并且对噪声也具有鲁棒性；文献［16］提出的ECC（Ensemble of Classifier Chains），ECC是基于CC（Classifier Chains）链式的集成多标记集成链式算法；以及文献［10］提出的混合噪声多标记学习（Hybrid Noise Oriented Multi-label Learning，HNOML）模型，HNOML 同时考虑了特征噪声和标记噪声并基于L2范数的图拉普拉斯矩阵考虑标记关联关系。

对于本文模型GNTML 的超参数λ1、λ2、λ3、λ4，本文从集合｛10-4，10-3，…，102｝通过网格搜索策略确定每个参数的最值，对于k值设定为5，因为它的变化对模型性能影响不大。对于其余算法尽最大努力调参以达到最好效果。

4.3 实验结果

本文实验中随机从数据集中选出2/3 作为训练集，剩下1/3 作为测试集，由于实验存在随机性，本文实验重复运行30次，求得最后的平均值和标准差。本文所提模型与其他对比模型的实验结果如表2 所示，由于每个数据集都是随机划分的，因此表中每个评价指标给出最后结果的平均值和标准差，并将最优值标记为粗体，次优值标记为下划线，最后一行统计了各个算法分别取得最优值和次优值的次数。从表中可以观察到，本文提出的模型GNTML 在7 个真实数据集的5 个评价指标上，66.7%（28/42）情况下取得最优值或次优值，其中38.1%（16/42）的情况下取得最优值，28.6%（12/42）的情况下取得次优值，相比于其他算法有一定的优势。作为多标记学习的经典基本算法BR，由于没有考虑标记之间的关联关系，所以它的结果是很一般的，最优值情况为0%，次优值仅占11.9%。ECC 算法通过集成学习结合基方法，由于要将上一个预测的标记结果输入到下一个预测数据集中，所以考虑到了标记关联，因此性能要比BR 有了很大的提升，在19.0%情况取得最优值，21.4%取得次优值。ML-kNN 算法虽然在Scene数据集上能表现出优异性能，但是在其他数据集上表现却是一般，因此不是很稳定。HONML 模型算法也稍弱于GNTML。

进一步地，为了验证所提出的模型在特征噪声和标记噪声共现时的鲁棒性，本文在Emotion数据集上进行了噪声鲁棒性实验。本文同时给训练样本的特征矩阵和标记矩阵人工添加噪声来模拟特征噪声和标记噪声共现的场景。具体地，对于特征矩阵，本文选取了0%～20%的样本添加特征噪声，每个选中的样本将其50%的特征值数值置为0，对于标记矩阵；本文同样选取了0%～20%样本添加标记噪声，每个选中的样本将其50%的标记值从正例变为负例，负例变为正例。

实验结果如图2 所示，从图2 中可以观察到，在数据集Emotion上，ML-kNN算法在不添加噪声时性能优于其他算法，但是随着添加噪声比例的增加，性能有所下降，HNOML 算法是基于L2范数的图拉普拉斯平滑假设，并且能处理混合噪声，表现也比较稳定，本文的方法用图趋势过滤代替基于L2范数的平滑假设，性能优于HNOML，也因此证明了本文模型中图趋势过滤项的有效性。

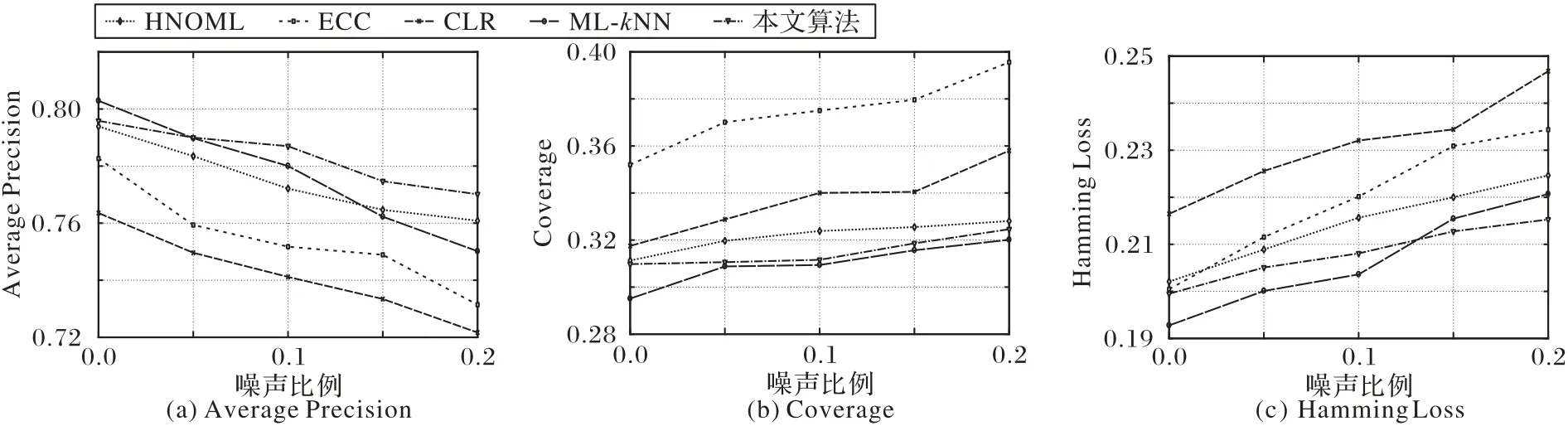
图2 在数据集Emotion上不同噪声比例下的鲁棒性实验Fig.2 Robustness experiments with different noise ratios on Emotion dataset

4.4 收敛性

本文提出的模型GNTML通过交替方向迭代优化求解，图3是数据集Birds和CAL500上的收敛情况，可以看出随着迭代次数的增大，模型的收敛速度很快，并且通常不超过10 次就能稳定。

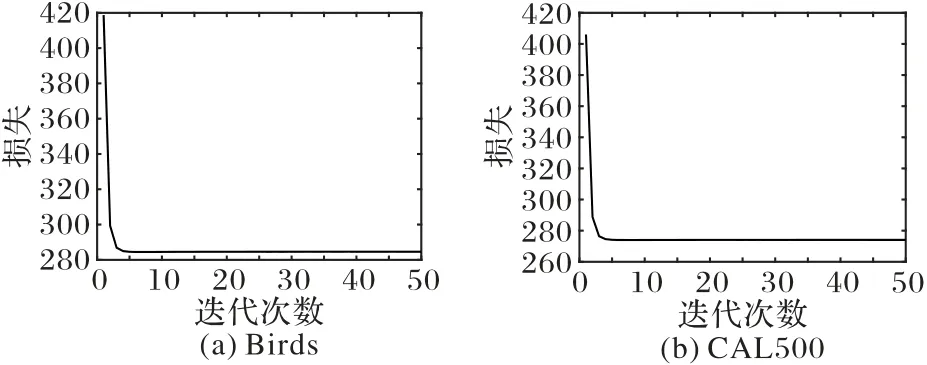
图3 本文算法在数据集Birds和CAL500上的收敛性实验Fig.3 Convergence experiments of the proposed algorithm on Birds and CAL500 datasets

5 结语

考虑到训练样本可能同时存在特征噪声和标记噪声，本文提出了一个图趋势过滤诱导的噪声容错多标记学习模型，这个模型通过挖掘标记之间的关联关系，增强原始标记空间，并结合组稀疏来同时处理特征噪声和标记噪声。本文采用图趋势过滤不仅保留了数据的局部特性，也可以容忍含噪示例特征与标记之间关联的不一致性，从而减轻特征噪声对标记增强矩阵学习的影响。在多个真实数据集上的实验也证明了所提模型的有效性。在后续工作中，计划将本文的模型推广到多视图情形，通过探索示例的多视图特征来进一步减轻特征噪声对多标记学习性能的影响。