基于邻居信息聚合的子图同构匹配算法

徐周波，李 珍，刘华东，李 萍

（广西可信软件重点实验室（桂林电子科技大学），广西桂林 541004）

0 引言

图匹配技术被广泛地应用于社交网络、网络安全、计算生物学和化学等领域［1］中。子图同构问题是图匹配问题中的一种，属于NP 完全问题［2］。研究者们从不同的角度进行研究，致力于提高子图同构问题的求解效率，并扩大求解规模。因此，子图同构问题成为图匹配问题中研究的热点。

求解子图同构问题的方法一般分为3类［3］：基于树搜索的求解方法、基于索引的求解方法和基于约束满足问题（Constraint Satisfaction Problem，CSP）的求解方法。Ullmann［4］首次提出了基于回溯的树搜索算法（以下简称Ullmann 算法），该算法基于全局搜索剪枝策略，一一枚举目标图与模式图中的节点对应的子图，由于该算法没有运用剪枝策略来对候选节点进行过滤，因此随着图数据量的增加其搜索复杂程度将呈指数增长。Cordella 等针对已匹配节点的邻接点启发式信息，给出了VF［5］及VF2［6］算法。VF2 算法基于Ullmann 算法按照节点度的大小依次选取模式图节点，以深度优先匹配顺序，结合匹配节点的1步和2步邻居信息来缩小值域范围以提高求解效率，是目前主流的子图同构算法。但VF2 算法并没有定义匹配顺序，针对这一问题，Carletti 等［3］提出了基于VF2 算法的VF3 算法。VF3 算法通过为模式图的节点计算选择概率来决定匹配顺序，引入分类概念将节点进行分类，并在搜索过程中引入向前看策略，更进一步修剪了搜索空间。但正因为引入概率选择和分类，具有较长的预处理时间。McGregor［2］首次给出了子图同构问题的基于节点的CSP 模型，并利用子图同构的路径一致性技术，求解子图同构问题。在此基础上，Larrosa 等［7］引入相邻约束，通过同态传播来删除各变量的不可行解。在将图匹配问题转化为二元CSP 过程中，会造成全局语义的丢失现象，为此Solnon［8］引入了一种全不同约束，通过此约束构建的CSP 模型相较于传统的CP 的过滤算法，具有更高的求解效率。Audemard 等［9］在Solnon［8］方法的基础上，增加相邻变量域的评估值进一步缩小值域范围。总体上，基于CSP 的求解方法，利用图中的属性和结构信息，结合传播约束、弧一致性等技术，迭代地在所有可能的节点对中过滤掉一定不是解的节点对，算法的优点是求解速度快，但是需要保留不满足约束的节点以避免重新搜索，因此对内存的需求大。基于索引的求解方法，这类方法通常以包含图的结构和语义信息的向量或特征树建立索引。Shasha、He 和Zou 等以路径、树结构作为过滤特征，给出了GraphGrep［10］、Closure-Tree［11］和Gcod-ing［12］等算法。算法首先查询模式图是否存在于目标图中，并建立相对应的索引，并在最后进行子图同构检测。索引信息越丰富，其检索的效率越高，但随之而来的问题是需要花费大量的时间来进行索引的建立。

对于如何提高子图同构的求解效率，现有的研究主要是从两方面入手：一是优化匹配顺序［13］，以减少搜索次数；二是使用更多的邻居关系来构建约束，过滤不可行的解，以减小搜索空间。对于匹配顺序的优化，本文通过考虑模式图和目标图中的节点的度和标签等属性，计算出匹配节点的Rank 值，并对Rank 值进行排序，得出优化后的匹配顺序，以此来为变量序进行赋值。现如今采用邻居关系来构建的约束，大多数是基于单个节点和单个邻居之间的约束关系，很少有考虑到节点局部邻域之间的信息。随着图卷积神经网络（Graph Convolutional Network，GCN）［14-15］的出现，可以很好地对图结构的空间信息进行特征的提取，将节点的局部邻域信息转化为节点的特征向量来进行表示学习。本文通过引入图卷积神经网络技术对模式图和目标图的节点的结构、属性特征进行邻居信息的聚合，使节点带有局部邻域的信息。

本文将采用树搜索方法并结合CSP求解技术对子图同构问题进行求解，利用优化后的匹配顺序对变量序进行赋值，并将节点局部邻域关系转化成约束，来提高子图同构求解的效率。通过一些公开数据集的实验分析表明，与经典的树搜索算法和约束求解算法相比，本文算法有效地提高了子图同构的求解效率。

1 相关定义

定义1图。是一个图，V是顶点集，E⊆V×V是边集，L=是一个标签集，V中每个节点都有一个顶点标签vlabel，且vlabel∈lv。E中的边都有一个边标签elabel，且elabel∈le。

定义2子图同构。给定目标图Gt=和模式图以及映射R⊆Vt×Vp，若存在单射函数f：Vp→Vt满足：

1）∀u∈Vp，存在f(u) ∈Vt，使得且lv(u)=lv(f(u))。

2）∀u，v∈Vp，u≠v⇒f(u) ≠f(v)。

3）∀(u，v) ∈Ep，存在 (f(u)，f(v)) ∈Et，且le(u，v)=le(f(u)，f(v))。

那么称Gt的子图sub(Gt)与Gp是子图同构关系，记做sub(Gt)≅Gp。

子图同构问题是指在目标图Gt中找到一个或所有与模式图Gp同构的子图。本文的算法是求解所有同构的子图。定义3CSP。约束满足问题定义为三元组其中：

1）X={x1，x2，…，xn}为包含n个变量的有限集合；

2）D={D(x1)，D(x2)，…，D(xn)}为n个变量的值域；

3）C={c1，c2，…，cm}为约束集合，约束ci的变量范围var(ci)={xi1，xi2，…，xij}，且对应的值域val(ci)⊆Dil×Di2×…×Dij(i=1，2，…，m，1 ≤j≤n)，其中xil∈X(l=1，2，…，j)，Dil为变量xil的值域，称ci为定义在变量集{xi1，xi2，…，xij}上的j元约束。

CSP 的解指的是对变量集X中的所有变量找到完全实例化，并满足约束集C中的所有约束。解决CSP 主要有三种算法：回溯搜索、局部搜素和动态编程，其中回溯算法为应用最广的算法。

2 基于节点邻居信息聚合子图同构匹配算法

首先，利用图卷积神经网络技术进行特征表示学习，得出包含节点局部邻域信息的特征向量；其次，根据模式图与目标图节点的标签、度等属性对匹配顺序进行优化；最后，构建子图同构的CSP求解模型并采用回溯算法对其进行求解。

2.1 邻居信息聚合

邻居信息聚合将对图的节点进行邻居信息的聚合，使只有自身属性特征的节点带有局部邻域信息，并以向量的形式表示出来。文献［15］所提供的聚合方法主要是针对节点分类，面对子图同构问题时，不能将提取的空间特征信息很好地转换为匹配时所需要的权值。鉴于此，本文对文献［15］的聚合方法进行了改进。

已知模式图Gp和目标图Gt，首先，利用模式图和目标图的结构属性特征，分别构建模式图Gp和目标图Gt的特征矩阵，并根据式（1）进行节点信息的传播和汇聚：

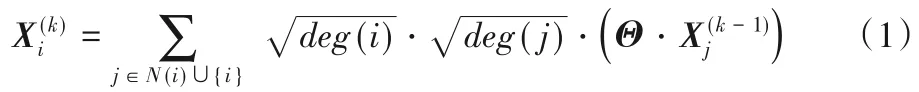
其中：N(i)为节点i的所有邻居节点集合，deg(i)为节点i的度，Θ是权重矩阵即机器学习中要更新的参数矩阵，为节点i第k次迭代的特征向量。

如图1所示，图1（a）为k=1时黑色节点的邻居信息聚合示意图，图1（b）为k=2 时黑色节点的邻居信息聚合示意图。在图1（a）中，黑色节点经过图卷积神经网络，对一步邻居信息进行汇聚，并得到新的节点特征向量。与图1（a）类似，图1（b）是两步邻居信息的聚合。在图卷积神经网络中是对每个节点进行聚合。

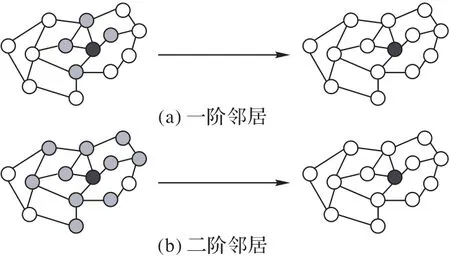
图1 不同k值时的邻居信息聚合示意图Fig.1 Neighbor information aggregation with different k value

其次，计算节点的权重值Weight。将得到的节点的特征向量进行降维操作，并对其取模，即可得到每个节点的权值。

2.2 优化节点匹配顺序

文献［9］指出节点的匹配顺序的不同会造成查询次数的不同，如图2 所示。针对模式图p给定两个匹配顺序O1={u1，u2，u3}和O2={u1，u3，u2}，若采用O1的匹配顺序与目标图g1进行匹配时：第1 步将u1与v1进行匹配；第2 步将u2与v2进行匹配；第3步将u3与v2的剩余的邻居v3进行匹配，发现标签不同不是同构子图，所以只需要匹配3 次就可以知道不是所需要的解。若采用O2的匹配顺序，第1 步将u1与v1进行匹配；第2 步将u3与v4进行匹配；第3 步将u2与v4的链接的邻居v5进行匹配，不满足匹配条件，但v4还有剩余邻居，则继续匹配，发现直到匹配到节点v1004还是不满足匹配条件，针对O2的匹配顺序则需要匹配1 003 次才能发现没有解；同理，若采用O1的匹配顺序与目标图g2进行匹配需要匹配1 003 次，若采用O2的匹配顺序，则只需要匹配3 次。由此可以看出不同的匹配顺序对搜索的次数是有很大的影响的。

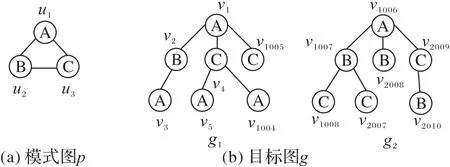
图2 模式图p和目标图gFig.2 Pattern graph p and target graph g

针对此问题，考虑到模式图中节点的标签属性出现次数少的应该优先匹配，并且节点的度数越大，节点就更具有特殊性。根据这一特性，给出式（2）对模式图节点进行排序，进行匹配顺序优化：

其中：freq(G，L(u))表示在目标图G中所有与节点u标签一致的节点总数量，deg(u)表示节点u的度。如图2所示，模式图p中节点u1在目标图g2中的freq(G，L(u1))=1，deg(u1)=2，则Rank(u1)=1/2。计算出模式图上每个节点的排序值，按照排序值的大小从小到大对模式图节点进行排序。若排序值相同，则随机排列，由此求出模式图节点的匹配顺序。

2.3 子图同构的CSP模型

1）变量集：X=Vp。

2）值域：∀xi∈X，D(xi)=Vt。

3）约束集C={c1，c2，c3，c4}：

a）边约束c1：∀xi，xi∈X，xi≠xj

b）节点标签约束c2：∀xi∈X，若xi=di，di∈D(xi)，则lv(xi)=lv(di)。

c）边标签约束c3：Ep，若xi=di，xj=dj，di∈D(xi)，dj∈D(xj)，则∈Et且le(xi，xj)=le(di，dj)。

d）全 不 同alldiff约 束c4：alldiff(x1，x2，…，xn)={(d1，d2，…，dn)|∀di∈D(xi)，∀i≠j，di≠dj，i=1，2，…，n}。

为了进一步对值域进行缩减，根据子图同构问题节点度的特性，在匹配时要求目标图Gt中节点的度数应当大于或等于模式图Gp中的节点，所以可将初始化值域Di更新为：

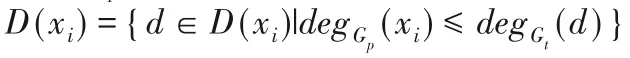
其中：degGp(xi)表示模式图Gp中节点xi的度，degGt(d)表示目标图Gt中与节点xi的映射节点的度。

在子图同构约束求解过程中，有效地构建约束是减小解空间、提高算法的时间效率的重要手段，基于2.1 节提出的邻居信息聚合方法，将得到的权重值Weight转化为聚合权值约束，在匹配时提供局部邻域信息，可进一步地缩减值域，提高算法的效率。进一步，在原约束集中加入邻域约束NDC，此时将CSP中的约束集更新为C={c1，c2，c3，c4，c5，c6}。

e）聚合权值约束c5：∀xi∈X，若xi=di，di∈D(xi)，则Weight(xi)≤Weight(di)。

f）邻域约束（Neighborhood Dominance Constraint，NDC）［9］c6：∀xi，xi∈X，若xi=di，xj=dj，则S(xi，xj)≤S(di，dj) 且(xi，di)∈N(xi)×N(di)，其中N(xi)是模式图节点xi的邻居节点，S(xi，xj)=MkGp[xi][xj]表示在模式图中节点xi到节点xj步长为k的路径数，S(di，dj)=[di][dj]表示在目标图中节点di到节点dj步长为k的路径数。

2.4 VFGCN算法

在VF2 搜索算法的基础上结合2.3 节给出的CSP 模型，并结合CSP求解技术给出基于图神经网络技术的子图同构算法（VF2 algorithm based on Graph Convolutional Network，VFGCN）。算法主要分为4 个步骤：第1 步为各个变量初始值域，根据度约束和节点标签约束对值域进行预处理；第2 步为邻居信息聚合，利用图卷积神经网络对节点进行信息聚合；第3 步为求解匹配顺序，为后续优化变量匹配顺序做准备；第4步为约束求解，对于不满足约束条件的解进行回溯。给出伪代码如下。

算法1 VFGCN。

输入 模式图Gp=(Vp，Ep，Lp)和目标图Gt=(Vt，Et，Lt)；

输出 所有的子图同构结果solutions。

算法第1）行函数Ri根据模式图和目标图节点的度和节点的标签属性为每个变量返回初始值域，对值域进行预处理，对于不满足条件的值从各个变量的值域中进行剔除。第2）行函数Neighbor函数用于对模式图和目标图的节点进行邻居信息聚合，根据式（1）将节点的局部邻域信息提取为节点特征向量并进行降维、取模等操作将向量转化为权值，并返回每个节点的权值，每个顶点的权值将作为后续回溯过程的约束条件。第3）行函数Rank 用于对模式图节点的匹配顺序进行优化，根据式（2）对模式图节点节点进行计算和排序，返回排序后的模式图节点匹配顺序S，返回后的顺序S即为求解时变量的匹配顺序，以优化后的顺序来为变量进行赋值。算法第4）～15）行为算法的搜索回溯过程，依次从返回的排序的节点序列S中选取变量，结合CSP 基于回溯的求解方法，若当前的值域满足Weight权值约束c5、NDC 邻域约束c6、边约束c1和边标签约束c3，则通过alldiff约束c4更新剩余待匹配变量的值域，保持单射关系，并将该变量从当前变量域中移除。若变量域中的变量并未完全实例化就引起值域的空值化，则说明当前搜索分支无法找到可行解，则算法向上回溯重新进行赋值；若变量完全实例化，即当前变量域为空，且对应的变量赋值满足所有约束条件，则说明找到一个可行解，并将可行解加入到最终解集中。

3 实验结果及分析

在Core-i5-6500@3.2 Hz，16 GB 内存的实验环境下，操作系统是Windows 10，64 位，编译环境是pycharm，编译语言是python。实验使用了公开数据集AIDS（http：//jenalib.leibnizfli.de）和PDBSV2（http：//www.rcsb.org）两个数据集，其中AIDS 为抗艾滋病毒数据集，包含大量的稀疏无向图，节点数量从4 到245 不等，每个图表示化合物的拓扑结构，并包含节点标签和边标签。目标图数据集中含有10 000幅图。模式图按边的数量分为Q4、Q8、Q12、Q16、Q20、Q24 六组，每组包含1 000 幅小图。PDBSV2 数据集为蛋白质骨架数据集，该数据集包含40 种蛋白质，为中等稀疏图，节点数量从4 000 到12 000 不等。目标图为40 幅大图，模式图按边的数量分为Q4、Q8、Q16、Q32、Q64、Q128六组，每组包含40幅小图。模式图均为按照边数从相应的目标图中随机抽取。实验过程中将使用本文算法与VF2 算法［6］、迭代标记过滤（Iterative Labeling Filtering，ILF）算法［16］、基于路径的局部全不同（Path of Local All Different，PathLAD）算法［17］、VF3 算法［3］相比较。实验结果中的平均时间通过式（3）计算得出：

其中：timeall为各个分组求解的总时间，Numpattern为每个分组中模式图的数量。平均时间更能体现求解单个模式图与所有目标图的子图同构全部解的时间效率，并统计出两个数据集进行邻居信息聚合时所花费的时间，计算公式与式（3）一致，timeall为模式图各个分组或目标图聚合总时间，Numpattern为各个分组中模式图的数量或目标图的数量。

基于上述所述，本文算法利用图卷积神经网络，对模式图和目标图节点的邻域特征信息进行了提取，并对匹配顺序进行了优化，减少了搜索次数，结合CSP 求解技术，提高了子图同构问题的求解效率。

1）首先在AIDS数据集上进行对比实验，按照模式图的规模将实验分为6 组。实验结果如表1 所示，由表1 中的数据可知在6 组实验中，VFGCN 算法均优于VF2 算法、PathLAD 算法、ILF算法和VF3算法；并且随着模式图规模的增大，求解的平均时间总体呈上升趋势。由此可以看出，模式图的大小对于求解时间的影响；但当模式图规模为Q24 时，时间却不是6组中最慢的，但解的个数是6 组中最少的。原因在于：在搜索的过程中，已提前对不可行的解进行了剪枝，避免了对无效的分支进行搜索，所以尽管模式图的规模是最大的，但是时间并非最慢的，因此模式图的规模大小对求解时间还是有很大的影响。

AIDS 数据集的邻居信息聚合时间如表2 所示，对于不同规模的下的模式图和目标图，聚合的时间大约都在0.001 4 s左右，由此可以看出聚合步骤所消耗的时间是非常少的，并且不受模式图规模的影响。因为不需要重复遍历图的所有节点，只需要遍历节点的有限邻居，所以能够在极短的时间内有对节点的局部邻域信息进行聚合，并给出其特征向量，并且在聚合时所选的k值（k步邻居）影响着后续的求解效率，在实验过程中发现，并不是聚合的邻居信息越多，即k取值越大，求解效率就越高；反而当k的取值超过一定范围，将降低求解效率。其原因在于，当k取值过大时，会使得聚合后的特征向量趋于一致，即所有节点的邻域信息过于相似，导致在后续的匹配过程中不能够很好地对不可行的解进行剪枝，反而影响了求解的效率。经实验测试，对AIDS 和PDBSV2 数据集来说，由于模式图的最大规模分别为Q24 和Q128，节点的邻居大多数是在3 步之内，所以将k取1 时效率是最高的，因此在后续的实验过程中k取值为1。

2）本组将在PDBSV2 数据集上进行对比实验，实验将按照模式图的规模分为6组。其邻居信息聚合时间如表2所示，对比表2 两个数据集聚合的平均时间可以看出，在不同的规模下，PDBSV2数据集的平均聚合时间均比AIDS数据集要长，其原因在于节点的邻居个数。PDBSV2 数据集整体的图密度要比AIDS 数据集要高，就是相对于AIDS 数据集，PDBSV2 数据集中的一个节点可能拥有着更多的邻居，因此在聚合过程中将花费更多的时间。

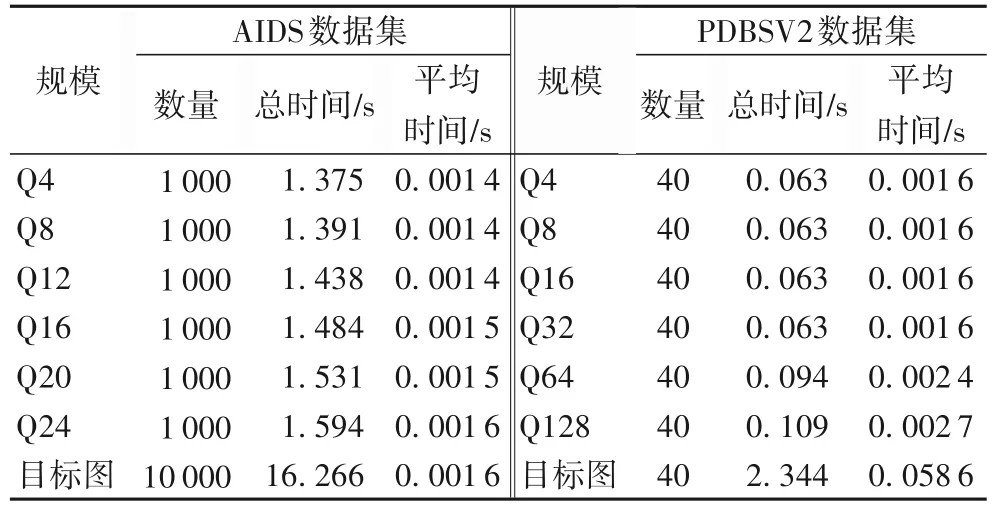
表2 邻居信息聚合时间Tab.2 Neighbor information aggregation time

与其他算法的对比实验结果如表3 所示。从表3 中的数据可以看出，随着模式图规模的增大，求解的平均时间总体呈上升趋势。VFGCN 算法求解的平均时间对比VF2 算法、ILF 算法和PathLAD 算法在6 组实验中均是最短的，对比VF3 算法在规模为Q64 和Q128 时VF3 算法略有优势。其原因在于，VFGCN 算法对节点的匹配顺序进行了优化，降低了搜索次数，并提取了节点的局部邻域信息，对于不可行解更有效地进行了剪枝。但是在规模为Q64 和Q128 时，VF3 算法首先对模式图中的节点计算匹配概率以此来确定匹配顺序，并对节点进行分类，不属于同一个类别的节点不能够进行匹配，在面对规模更大模式图的时候比VFGCN 算法更能对值域进行修剪。但是同样，VF3 算法在计算规模偏大的模式图节点的选择概率和对节点进行分类时，所耗费的预处理时间也更长了。

表3 PDBSV2数据集上的实验结果Tab.3 Experimental results on PDBSV2 dataset

4 结语

为了进一步提高子图同构问题的求解效率，本文提出了一种基于邻居信息聚合的子图同构匹配算法，能够有效地缩减值域。该算法结合图卷积神经网络技术，利用改进后的聚合公式，对模式图和目标图的节点进行局部邻域信息的提取及聚合，并且基于图的标签、度等特征提供了一种优化后的匹配顺序，建立子图同构的CSP 求解模型并进行回溯求解。实验结果表明，该算法与经典算法相比较，有效地减少了子图同构的求解时间，在小规模以及中等规模的图匹配中有较高的求解效率。在未来的工作中，将研究动态图匹配算法，并结合CSP技术中的动态CSP求解技术对其进行求解。