Study on a LPs control algorithms in SCARrobot
Xin-wen BI,Yan-ming CHENG*,Lin BI,Cheng LIU
(1 Beihua University,Jilin 132021,China)
(2 College of Optoelectronic Engineering,Changchun University of Technology,Changchun 130012,China)
Abstract:In the traditional robust control method,the uncertain boundary is needed in the design of the control law,however,the boundary usually increases the amplitude of the control signal and causes damage to the system.Therefore,this paper porposes a kind of LPs(Legendre polynomials)control law.The total uncertainty of each joint of SCAR Robots is estimated,accordingly,the uncertain boundary is calculated by LPs.Compared with the traditional robust controller,the proposed controller is simpler,requires less computation and less feedback,and eliminates the condition that the upper limit of external interference and parameter uncertainty must be known in advance.The control law proposed is simulated by a SCARA robot manipulator,and the simulation results verify the effectiveness of the proposed control method.
Key words:Uncertain boundary,Robust control,LPs control law
1 Introduction
In the past decades,the adaptive control and robust control of robot manipulators have been extensively studied in task space[1]and joint space[2].Robust and adaptive control are considered important because they can overcome the uncertainty between the nominal model and the actual model due to mismatches.External disturbances,parametric uncertainties and unmodeled dynamic characteristics are the main sources of uncertainty in control engineering,which seriously affect the performance of the controller.In the early studies of robust control methods[3],controller designs are often based on nominal models.A robust control term is then added to the control law to compensate for the uncertainty,which needs to be determined by the Lyapunov stability analysis.In these methods,uncertain boundaries need to be used to determine the stability of the system and design the control law.Normally this boundary is the upper limit of the system state and external disturbance.Therefore,all required feedback should be available,and the upper limit of parameter uncertainty and external interference should be known in advance.In addition,the linear parameterization of the manipulator kinematics equation is necessary in most robust and adaptive control methods[4].The controller motion equation should be modeled completely to determine the regression matrix.
Most of the research in the field of robot control is based on the torque control strategy(TCS).But oftenTCSignores the dynamic performance of the drive.In order to solve this problem,a simple and convenient voltage control strategy (voltage-based controller,VCS)was proposed.Voltage-based manipulator controller stability analysis has been studied[4-5].Then on the base of the VCS,scholars have proposed different robust control methods[6-7].Recently,a number of adaptive control methods for regressions have been proposed[8],and the uncertainty has been estimated by using the Fourier series.Based on the Lyapunov stability,some adaptive rules are deduced to adjust the Fourier series coefficients.According to,some other orthogonal functions,such as Legendre and Chebyshev polynomials,can be approximated to continuous time functions at arbitrary precision[9].In this paper,this idea is used to estimate the uncertain boundary of the robot task space control for the electrodynamic robot.
Motivated by the aforementioned analysis,this paper presents a simpler method compared with the literatures[10-11].In this paper,the lumped uncertainty for each joint is estimated.Another advantage of the proposed model is that it eliminates the need to know in advance the conditions for external disturbances and the upper limit of the parameter uncertainty.
2 A traditional robust control method using VCS
According to literature[12],a robot system including a manipulator and a permanent magnet DC motor can be described by the following nonlinear state space equation.
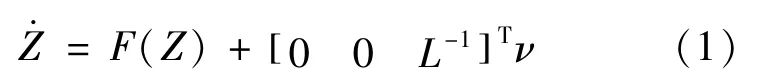
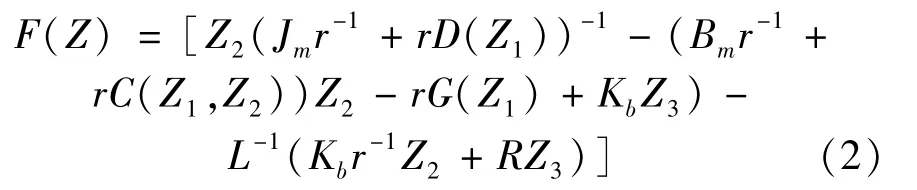
Where,D(Z1)is the inertial n×n matrix of the manipulator;C(Z1,Z2)Z2∈Rnis the centrifugal force and Coriolis force vector;G(Z1)∈Rnis the gravity moment vector;Jm,Bm,and r are the diagonal matrix of the motor inertia,damping and deceleration gear coefficients,respectively;v∈Rnis the motor voltage vector;R and Kbrespectively represent the armature resistance and counter electromotive force constant coefficients of n×n diagonal matrix;In this paper,it is assumed that the nonlinear vector function F(Z)is unknown.
The position and velocity in the task space are denoted by X∈R3andrespectively.The joint space velocity vector˙q and J(q)∈R3×nare associated with the task space velocity vector X·expressed by

The matrix form of the electrical equations of a permanent magnet DC motor is expressed as
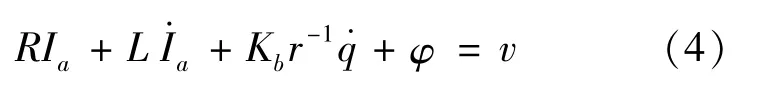
φ∈Rnis the external disturbance vector,which can be obtained by literature[9]. This paper assumes that the manipulator runs in a range where J-1(q)is nonsingular.Equation(4)can be written as
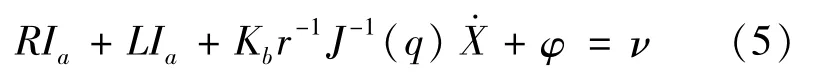
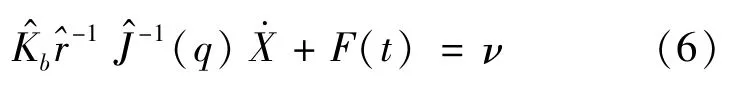
Here F(t)is the lumped uncertainty,which can be derived from Equation(5)and(6)as
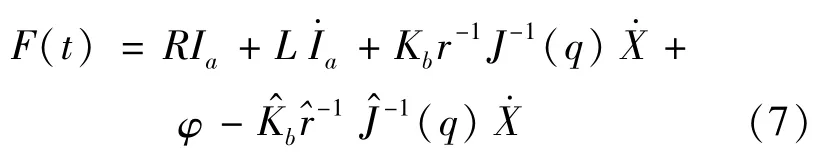
As stated earlier,undetermined boundaries are required in most robust control methods.Therefore,suppose that the bounded uncertainty function F(t)in Equation(7)iswhere the scalar functionη(t)is given by
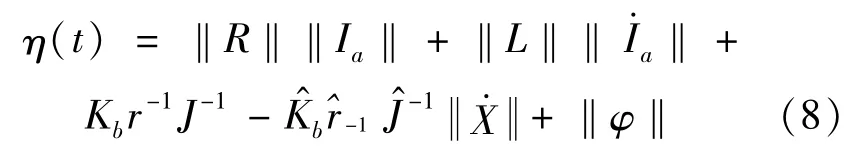
A robust control law is proposed for the system expressed in Equation(6)as
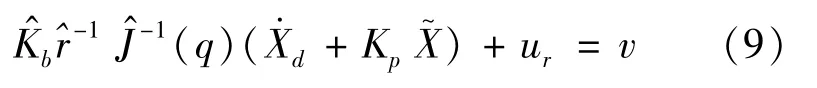
3 Put forward control rules
The robust term ur[9]requires that the boundaryη is not determined.According to Equation(8),ηis a function of the motor current Ia,its derivativeand the mission space velocity X·.These signals should be measured and fed back to the controller.In most realtime applications,the motor current and its derivatives of time are overwhelmed by noise.Thereby,their use in the control law may reduce the performance of the controller.In addition,the maximum values of‖R‖,and‖φ‖ are required.In order to solve this problem,the uncertain boundaryηis estimated by LPs.
Closed-loop system,can be written as

According to the orthogonal function theorem[9],the uncertain boundaryη(t)in Equation(8)can be estimated by Legendre polynomial

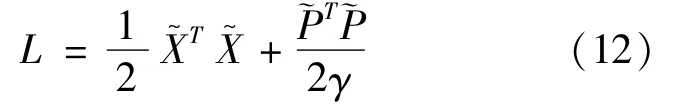
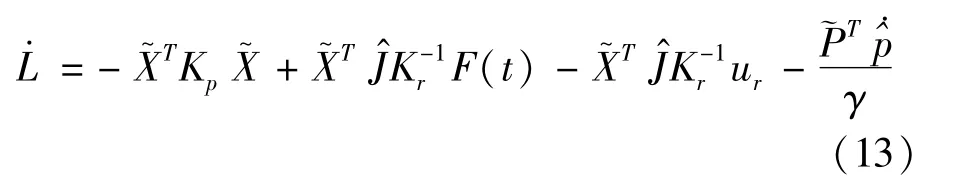
The upper limit of F(t)isη(t),therefore,according to Equation(13),
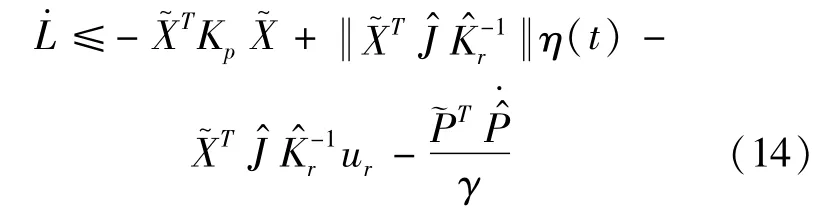
uris described in[10],hereSubstitutingandμfrom Equation(14),
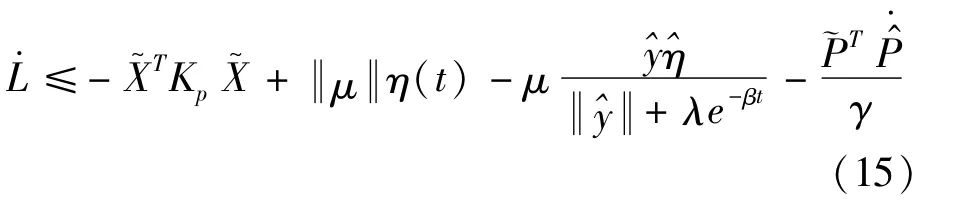
Equation(15)can be rewritten as

By Equation(16)
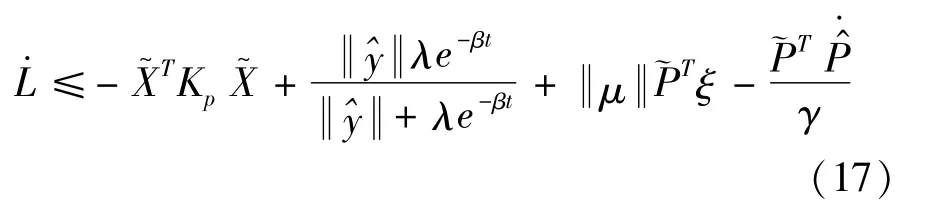
Taking into consideration the adaptive rule^=γ‖μ‖ξ,Equation(17)can be simplified as
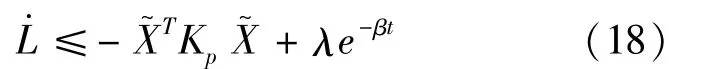
This indicates that the tracking errorconverges to zero asymptotically[14],the vectoris bounded.According to the literature[10],the state vector Z=is bounded.Therefore,the proposed control law is
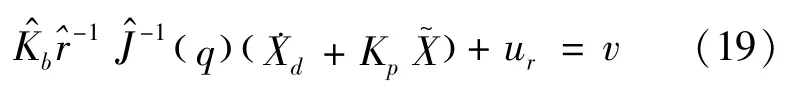
4 Simulation results
The control law proposed in this paper is simulated by a SCARA robot manipulator.The specific parameters and cost functions are described in[11].The parameterγis chosen to be 1 000,and the initial value of LPs is selected at random.Uncertain boundary η(t)can be estimated according to Equation(11).P^on-line adjustment using adaptive rules.In order to make the estimation error as small as possible,the number of orthogonal functions of vectorξshould be increased.Fig.1 shows the tracking performance in the XY plane.
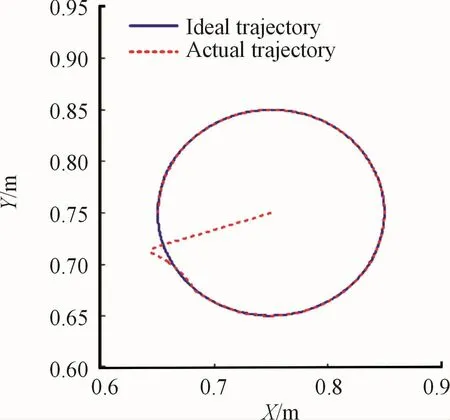
Fig.1 Tracking the performance of the XY plane
The value of parameter is chosen to be 1 000,andthe initial value of LPs is selected at random.Fig.2 shows the end of the tracking error of the actuator which meets requirements.
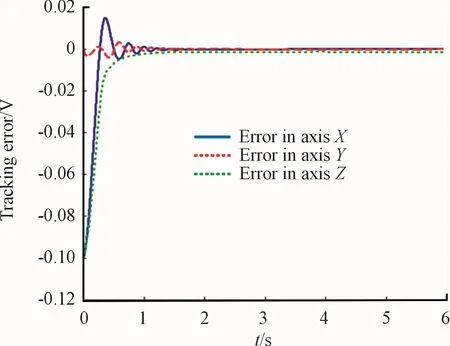
Fig.2 Task space tracking error
The control algorithm proposed control is shown in Fig.3,the motor voltage is smooth and does not exceed the maximum allowable voltage.The change and self-adaptation of Legendre coefficient are bounded.For the entire controller,the value is 0.037 09.According to the literature[12],for X,the term 11 is sufficient.Simulation results show that it is necessary to increase the number of LPs.To assess the estimated effect,we increase the size ofξto 13,15,17,and 19.For all simulations,Cfis approximately 0.037 09.
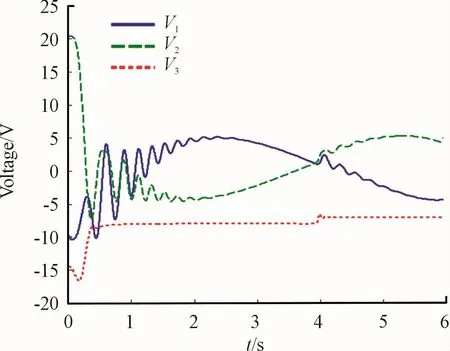
Fig.3 Control of the proposed algorithm
In order to evaluate the effect of parametric uncertainties,=0.5J()q and=0.25Kr are simulated,respectively.XY plane tracking error and motor voltage as shown in Fig.4 and Fig.5,the results shows that although the parameter uncertainty increases,the robustness of the controller is to meet the requirements.The value of the cost function Cfis increased to 0.068 92.
When evaluating effect of parameter uncertainties,it is assumed that the robust item uris0,then the cost function value increases from 0.037 09 to 0.069 41,which shows the effectiveness of the proposed method.
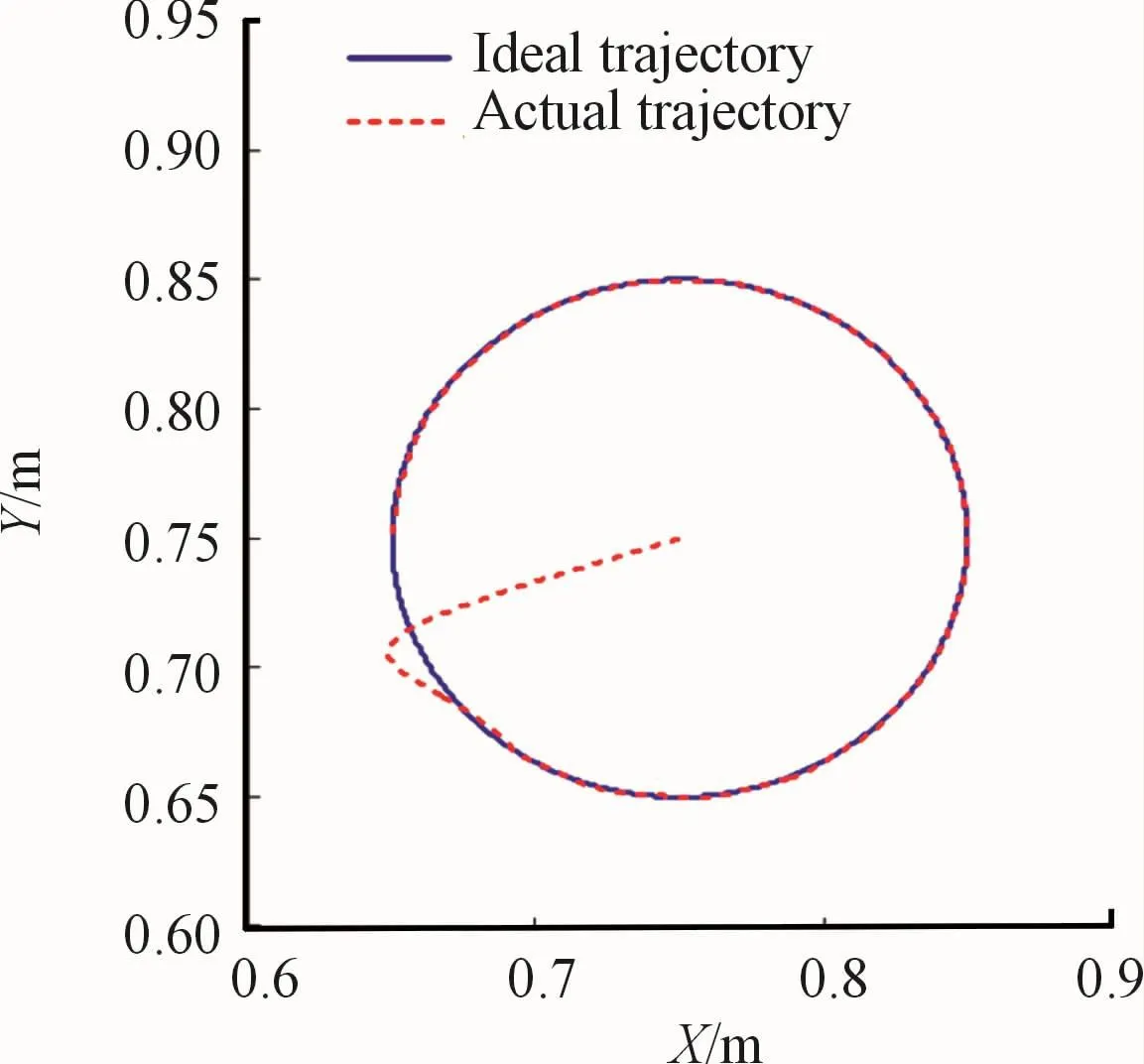
Fig.4 Tracking error in XY plane with increasing parameter uncertainties
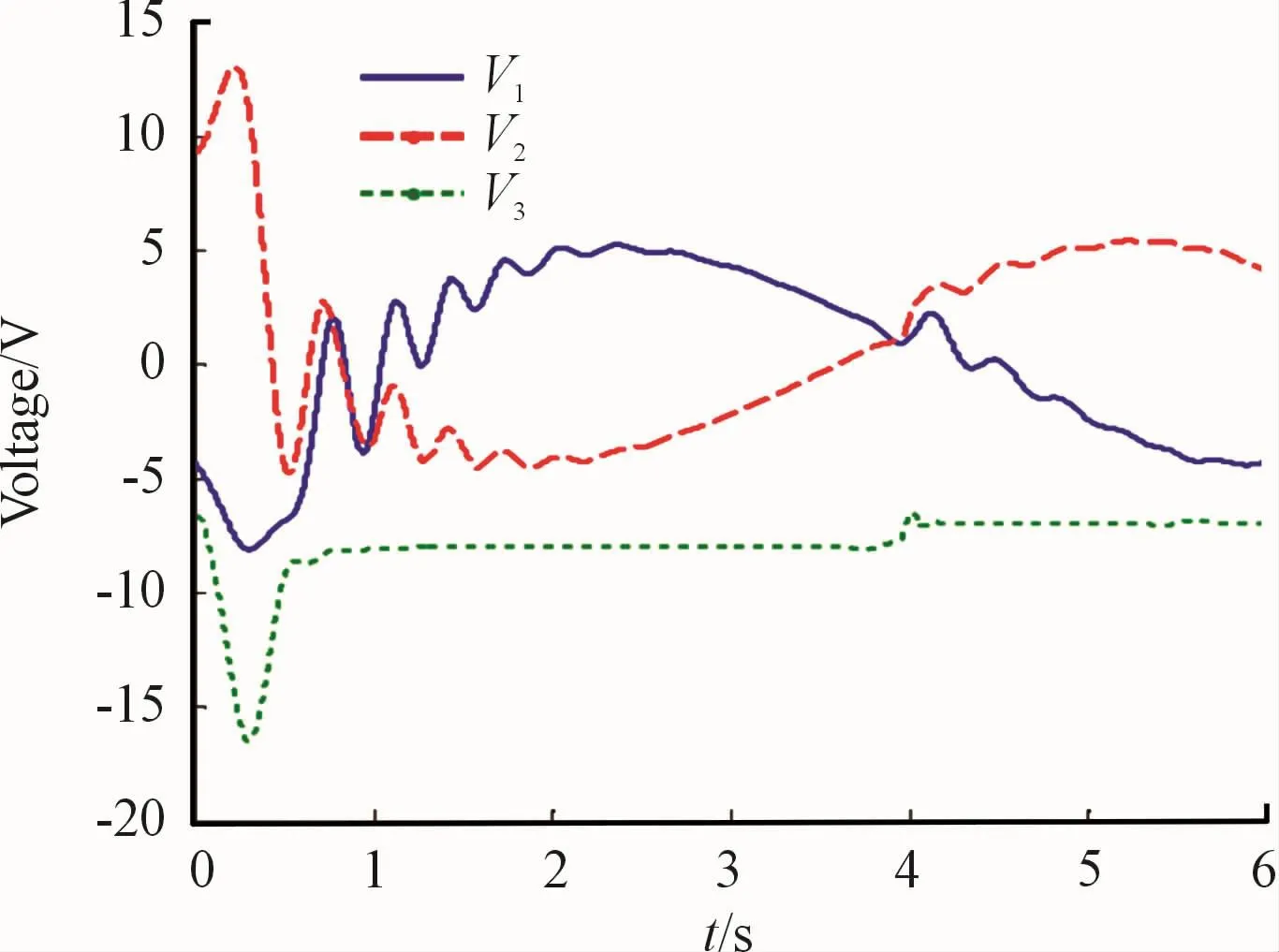
Fig.5 Control attempts in the case of uncertain parameters
5 Conclusion
Aiming at solving the problem that the traditional robust control method needs uncertain boundary as the function of the state system and external disturbance upper limit,and the feedback cost of the controller is expensive,and difficult to be realized.Therefore,this paper proposes a control law based on LPs and carries on the simulation analysis.The simulation results indicate that the advantage of the function approximation technique is that the number of feedbacks is much less than that of the traditional robust control method.
- 机床与液压的其它文章
- Analysis of cylindrical roller bearing with local damage based on multi-body dynamics
- Research of hydraulic gradient for large particle slurry in inclined pipeline
- Research on fault identification method of positive and negative fault subspace matrix
- Research on mechanism of intelligent manufacturing equipment based on eye tracking control
- Path planning for obstacle avoidance of mobile robot based on optimized A*and DWA algorithm
- Real-time recommendation based on comprehensive popularity of items

