Analysis of cylindrical roller bearing with local damage based on multi-body dynamics

Meng-ke YANG，Dan-xia HUANG，Zhi-qiang SHEN，Yun-bin LI，Hong-bin LIU*

（1School of Mechatronics Engineering，Henan University of Science and Technology，Luoyang 471000，China）

（2 School of Beijing Electronic Science and Technology Institute，Beijing 100070，China）

Abstract：In order to study the vibration response characteristics of bearing system with local damage，a dynamic model was developed based on multibody dynamics to predict the size，location and shape of local defects of the bearing，and the influence mechanism of defect parameters on bearing vibration was analyzed.The result shows that the vibration response of the bearing increases gradually with the increase of defect size.As the position of the defect moves away from the maximum bearing area，it will gradually decrease.The vibration response of the rectangular defect is the largest，triangular defect the second，and circular defect the smallest.The relationship between the vibration response of the cylindrical roller bearing and the size and location of local defects is obtained through a bench test，and the reasonableness of the dynamic analysis are verified by comparing with the simulation results.It will provide a theoretical reference for diagnosing the early failure mechanism of bearings.

Key words：Cylindrical roller bearing，Local defects，Dynamics analysis，Spectrum analysis

1 Introduction

Rolling bearings are key components in mechanical equipment.The normalcy of their working state is directly related to the production quality and safety of the entire unit and even the production line itself.During the operation of the bearing，surface damage such as pitting and fatigue spalling may occur on the surface of the bearing raceway，which will seriously affect the working state of the bearings.When the rolling bearing has local damage，the contact stress at the contact position between the local damage and its mating surface will change abruptly，resulting in very short pulse.This pulse will cause abnormal vibration of the bearing，and the presence of damage in the bearing can be detected by monitoring the vibration［1-2］.In the frequency domain analysis of bearing vibration，the failure frequency of bearing components is determined by the influence of damage pits on the outer ring，or inner ring，or cage of the bearing.Damage pits on rolling elements can also generate specific frequencies［3-4］.In this case，damage to the bearing element can be judged by comparing with the normal frequency spectrum of bearing vibration.Therefore，state monitoring based on vibration signal analysis can effectively monitor the state of the bearing system and predict the bearing damage in advance［5-6］.

A lot of research has been done by scholars at home and abroad to study the fault vibration characteristicsof rolling bearings.McFadden and Smith［7-8］established a dynamic model of single-point and multi-point local defects of rolling bearings in the earliest period.A periodic pulse function was used to simulate the impact of rolling bodies passing through the defects，and the influence law of single-point and multi-point local defects on the vibration characteristics of rolling bearings was studied.The results show that the frequency spectrum amplitude of rolling bearings is related to the degree of damage of bearings，and the phase of the peak value in the frequency spectrum depends on the locations of the defects.Li Guochao et al［9］established the dynamic model of the outer ring crack fault of the rolling bearing using ANSYS／LS-DYNA software，and studied the vibration response characteristics of the bearing under the outer ring crack fault.Arshan et al［10］put forward a dynamic model of the bearing system，and studied the influence laws of a single local defect on the vibration characteristics of an angular contact ball bearing on the inner ring，outer ring，and roller surface.In this model，a local defect was simulated by increasing the clearance between the roller and the raceway.Patel et al.［11］established a dynamic model of deep groove ball bearings with local defects，and studied the influence of single and multiple defects on the inner and outer raceway surfaces on bearing vibration characteristics.Ashtekar et al［12］proposed the expression of the relationship between the surface defect size of rolling bearing raceway and the contact force between the rollers.By establishing the dynamic model of the rolling bearing，the influence law of different defects on the contact force between the contact elements inside the bearing was analyzed.Ma Hui et al［13］established a twodimensional explicit finite element model of healthy cylindrical roller bearing based on ANSYS／LS-DYNA software，and analyzed the equivalent stress of the edge element in the fault zone and the process of roller rolling through the local defects of the inner and outer rings.Behzad et al［14］described the impact caused by local defects of rolling bearings as a random dynamic excitation force，and studied the influence law of local defects on the vibration response characteristics of rolling bearings.Liujing et al［15］used a piecewise function to model the local damage in bearings.Based on this dynamic model，the non-ideal Hertz line contact characteristics of cylindrical roller bearings after local damage were analyzed.Liao Yingying et al［16］analyzed the fault characteristic frequency of double-row tapered roller bearings in the normal state and outer ring peeling fault state by combining numerical simulation and experimental research.Niu Linkai et al［17］studied the dynamic modeling of local surface damage of bearings，taking into account the relative sliding and lubricating traction characteristics between the components，the additional clearance introduced due to material loss after damage，and the influence of damage on the Hertz contact stiffness and direction of contact load.However，in general，research on the vibration characteristics of rolling bearing faults is mostly focused on ball bearings，and the research on roller bearings is not extensive.Therefore，the establishment of a dynamic model for local defects in cylindrical roller bearings and the study of the influence of surface defects on the vibration response characteristics of cylindrical roller bearings can provide theoretical support for finding the influence mechanism of defects on the vibration characteristics of cylindrical roller bearings.

2 Dynamic modeling theory of rolling bearings

For rolling bearings，in order to describe the movement of the bearing and its internal components conveniently，an overall coordinate system and several local coordinate systems can be selected based on the characteristics of the rolling bearing，wherein the overall coordinate system coincides with the geometric center of the bearing and is fixed in space，and local coordinate systems are determined according to this coordinate system.The local coordinate systems of the rolling body and the cage coincide with their geometric centers.The difference is that the coordinate system of the rolling body moves with the rolling body but does not rotate with it.The local coordinate system of the cage moves and rotates with the cage.The bearing coordinate system is shown in Fig.1.

2.1 Basic theory of multi-rigid system dynamics

The dynamic analysis of a multi-rigid-body system is an analysis of the displacement，velocity，acceleration，and forces of a rigid body.For multi-body systems，the equations of motion of each rigid body are first established，and the dynamic equations of multibody systems are derived according to the Lagrange multiplier theorem.As shown in Fig.2，the position ofthe centroid of any rigid body in space can be determined by using the vector r and a set of generalized coordinates.Assuming the origin o′of the rigid body’s local reference coordinate system o′x′y′z′is the centroid of the rigid body，the Newton-Euler variational motion equation of the rigid body is：

WhereδrTandδπ′are the virtual displacement and virtual rotation of the rigid body，respectively，m is the total mass of the rigid body member，F is the resultant force of action on a rigid body，M is the total moment of the external force relative to the point o′of the local reference coordinate system，J′is the constant inertia matrix of external force relative to the coordinate system o′x′y′z′.

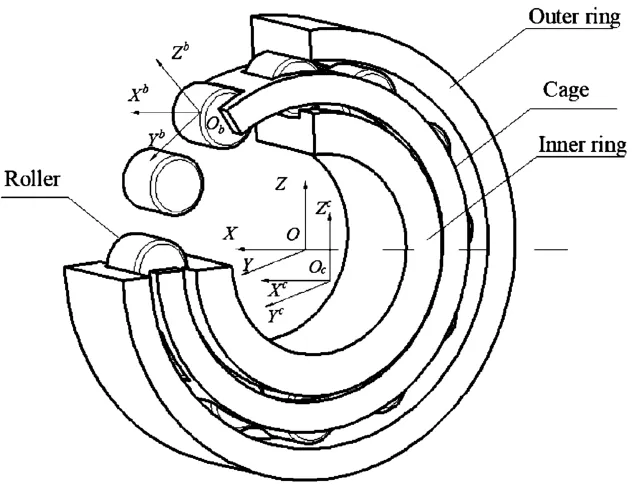
Fig.1 Cylindrical roller bearing coordinate system

Fig.2 Coordinate transformation in spatial

In order to establish the dynamic equation of the bearing system，it is necessary to select the coordinates of the center of mass of each system component in the coordinate system o′x′y′z′，and determine the three Euler angles of the component as generalized Cartesian coordinates，namely qi＝［x，y，z，Φ，θ，φ］，.Each component is described by six generalized coordinates，and n is the number of components in the system.The Lagrange equation is written in the matrix form，and the dynamic equation in the generalized coordinate form is expressed as follows：

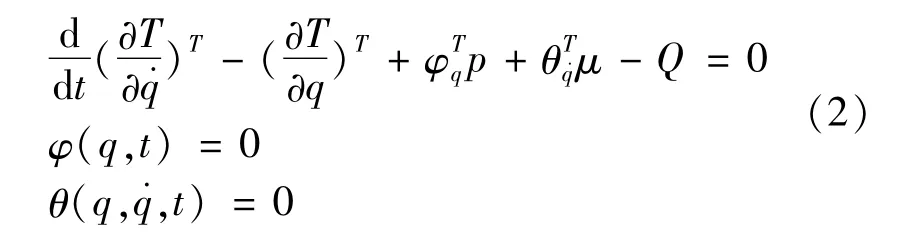
Whereφ（q，t）＝0 andθ（q，˙q，t）＝0 are the complete and incomplete constraint equations，respectively；p andμare，respectively，the Lagrange multiplier matrices corresponding to complete constraints and incomplete constraints；q is the generalized coordinate vector，T is the kinetic energy of the system，and Q is the generalized force.The kinetic energy T of the system is expressed by the generalized velocity as：

2.2 Bearing damage model

NF308 cylindrical roller bearing is selected，and its main structural parameters are shown in Table 1.In the dynamic system，a dynamic failure model of outer ring damage in a cylindrical roller bearing is established，as shown in Fig.3.Among them，the inner ring of the bearing is matched with the shaft to have rotary motion，and the radial load is applied to the outer ring of the bearing at the same time.The outer ring will not rotate and translate under the action of the radial load，but will generate slight vibration.Through the dynamic analysis of the bearing system，the influence of the local defects of the outer ring on the vibration of the entire bearing system during the operation period is determined.The following assumptions have been made for the dynamic model：

1）Regardless of the impact of external system vibration or noise on the vibration，the shaft and the inner ring of the bearing only rotate，and the outer ring of the bearing neither rotates nor translates；

2）The load on the bearing is assumed to be a concentrated force；

3）The contact deformation of the bearing is based on an extended surface to surface contact force unit and meets the Hertz contact conditions；

4）The bearing is assumed to work under isothermal conditions；

5）The influence of local defects on the bearing surface are accounted for，while the roughness of the bearing raceway and the fillet of the bearing are ignored.

Table 1 Bearing structural dimensions

Fig.3 Fault model of bearing outer ring

2.3 Contact stiffness and damping of bearings

The research on the dynamic characteristics of cylindrical roller bearings essentially considers the contact between the bearings as a spring-damper system，as shown in Fig.4，and analyzes the vibration characteristics of cylindrical roller bearings.The stiffness and damping coefficient of the bearing system are very important parameters in dynamic analysis.

Fig.4 Spring-damping model

Here，the stiffness coefficient k depends on the contact geometry between the roller and the raceway.According to the document［18］，the contact stiffness between the inner and outer rings of rolling bearings and rolling elements can be expressed by the following formula：

Here，Λ，K，andμare Hertz coefficients that depend on the surface characteristics.E，1／M，∑ρand rθiare the elastic modulus，Poisson’s ratio，contact curvature，and sum of radial displacement，respectively.

Kumer provided an estimation formula for bearing damping，in which the rolling element seat ring vibration system was simplified as a linear spring mass damping system.Based on the following evaluation，when harmonic motion occurs，the magnitude of the damping force is equal to the frequency of the spring force：

Where KBis the bearing stiffness matrix，f is the vibration frequency，andψis the loss factor.

2.4 Contact calculation

The contact force calculation formula in the dynamic model based on Hertz contact theory is as follows：

A very important problem in dynamics is the calculation of the contact force between system components.The calculation of contact force in the dynamics software is improved based on the Hertz contact theory.The contact roller-raceway contact calculation in the dynamics model is shown in Fig.5.In this dynamic system，contact calculation directly affects the accuracy of the results of the dynamic simulation.Contact parameters include stiffness，damping，and friction coefficient.The contact normal force is obtained by E-quation 8：

Here，k and c are the contact stiffness coefficient anddamping coefficient，respectively，δandare the contact penetrating depth and the derivative of the contact penetrating depth（the relative velocity of the contact point），m1，m2and m3are the stiffness index，damping index，and dent index respectively.The friction force in this system can be known from the following formula：

Here，fnandμare the contact normal force and friction coefficient respectively；νsis the static threshold speed；νdis the dynamic threshold speed；μsis the static limit friction coefficient；μdis the dynamic limit friction coefficient；μis the friction coefficient determined by the tangential velocity of v.The coefficient of friction is shown in Fig.6.

Fig.5 Contact calculation

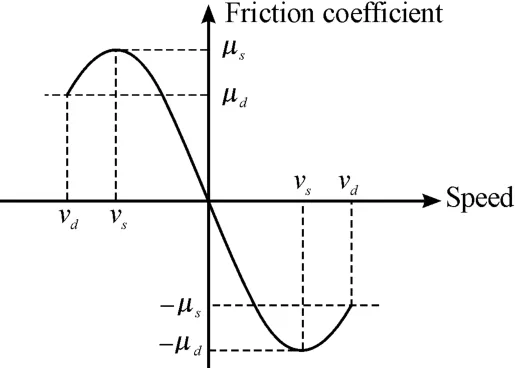
Fig.6 Graph of friction coefficient with velocity

3 Simulation calculation method

3.1 Initial conditions

Based on the above model，the vibration response of bearings with different defects during the operation was simulated.The damping coefficient between the contacts in the system was set to106N·s／mm；the elastic coefficient between the inner ring and shaft，inner ring，and rolling body，outer ring，and rolling body，and the rolling body and cage was 108N／mm；the static friction coefficient between the body and the inner and outer rings was 0.3，the dynamic friction coefficient was 0.15；the static friction coefficient between the rolling body and the cage was 0.002；the dynamic friction coefficient was 0.001；the static friction coefficient between the bracket and the outer ring was 0.8；and the dynamic friction coefficient was 0.5.A radial force was applied to the outer ring of the bearing system，the speed of spindle was set to 1800 r／min，the simulation time was set to 1 second，and the step length was set to 1024 to obtain the time-domain vibration signal of the bearing.

3.2 Time-frequency domain analysis of vibration signals

When the rolling bearing has defects，the vibration signal of the outer ring will show fault frequency.The fault characteristic frequency of rolling bearing components is：

Where DWis rolling element diameter（mm）；D is pitch diameter（mm）；N is number of rolling elements；fSis spindle frequency（Hz）.According to the above formula，the fault characteristic frequency of each bearing component can be calculated.See Table 2 for details.

Table 2 Bearing fundamental frequencies

Fig.7 shows a comparison of the vibration signal of the outer ring damaged bearing（width 0.2 mm，depth 0.05 mm）and the intact bearing in the time domain.From Fig.7，it can be seen that when the bearing is defective，the vibration signal of the bearing increasessignificantly in the time domain，which is due to the periodic behavior of the rolling bearing in the operation process.When the bearing has defects，the impact of the rolling body of the bearing increases each time it passes through the defects，thus causing the vibration signals of the bearing to increase.

Fig.7 Time domain signal contrast diagram of bearing

From the signal diagram in the frequency domain of Fig.8，it can be seen that whether the bearing is damaged or intact，the peaks all appear at the characteristic frequency in the spectrum diagram of the vibration signal.The fault characteristic frequency of the bearing is shown in Table 3.When a fault occurs at the outer race raceway of the bearing，the peaks of the outer race fault characteristic frequency（at 159 Hz）and its double frequency（at 318 Hz）obviously increase.The existing research results show that the amplitude in the frequency spectrum diagram of the rolling bearing is related to the degree of bearing damage，and the phase in the frequency spectrum diagram depends on the location distribution of local defects［19］.Therefore，the peak value at the characteristic frequency in the bearing vibration signal spectrogram can be used to check whether the bearing fails，and the peak value at the characteristic frequency can be used to characterize the degree of damage of the bearing.

Table 3 Comparison between theoretical calculation and experimental results

Fig.8 Bearing frequency domain signal contrast diagram

4 Results and analysis

4.1 Influence of defect shape on bearing vibration

Three different types of bearing outer ring failure models are established as shown in Fig.9.Fig.10 is the influence diagram of the change of the defect shape on the vibration amplitude of the bearing.It can be seen from the graph that there are obvious differences in the influence of different defect types on bearing vibration.The peak of the rectangular defect is the largest and the peak of the circular defect is the smallest.

This shows that in the case of local defects on the surface of rolling bearings，due to the different shapes of the defects，the impact waveforms induced when the rolling body rolls into or out of the damage pit are alsodifferent，resulting in great differences in vibration.In order to further study the influence of the defect shapes on the vibration response of the bearing，vibration displacement of the bearing outer ring，and contact force between the rolling element and the outer ring can be further analyzed.The steps of simulation are 10240 speed of rotation is 1800 r／min，and radial load on the bearing is 150 N.

Fig.9 Defect shape of bearing outer ring

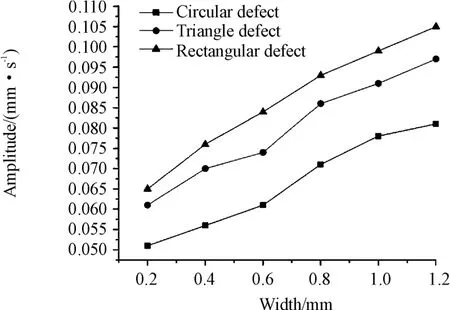
Fig.10 lnfluence of different types of defects on vibration amplitude of bearings

Since the bearing has periodic motion during operation，a periodic contact force and vibration curve can be selected for the analysis.Fig.11 is a graph showing the change in contact force between a roller and the outer ring during the operation of the bearing，and Fig.12 is a graph showing the change in contact force between a roller and the outer ring during a period of bearing operation.Fig.13 is the vibration displacement diagram of the outer ring for defects of different shapes.

As can be seen from Figs.11 and 12，during the operation of the bearing the existence of defects will cause the rolling body to generate a larger impact force when rolling in and out of the local defects，as shown at points A and B in Fig.12.The shock will cause the vibration displacement of the outer ring of the bearing to change.According to the vibration displacement of the outer ring of Fig.13，we can find that the vibration displacement of the outer ring has the largest fluctuation and largest vibration response when there is a rectangular defect in the outer ring of the bearing.

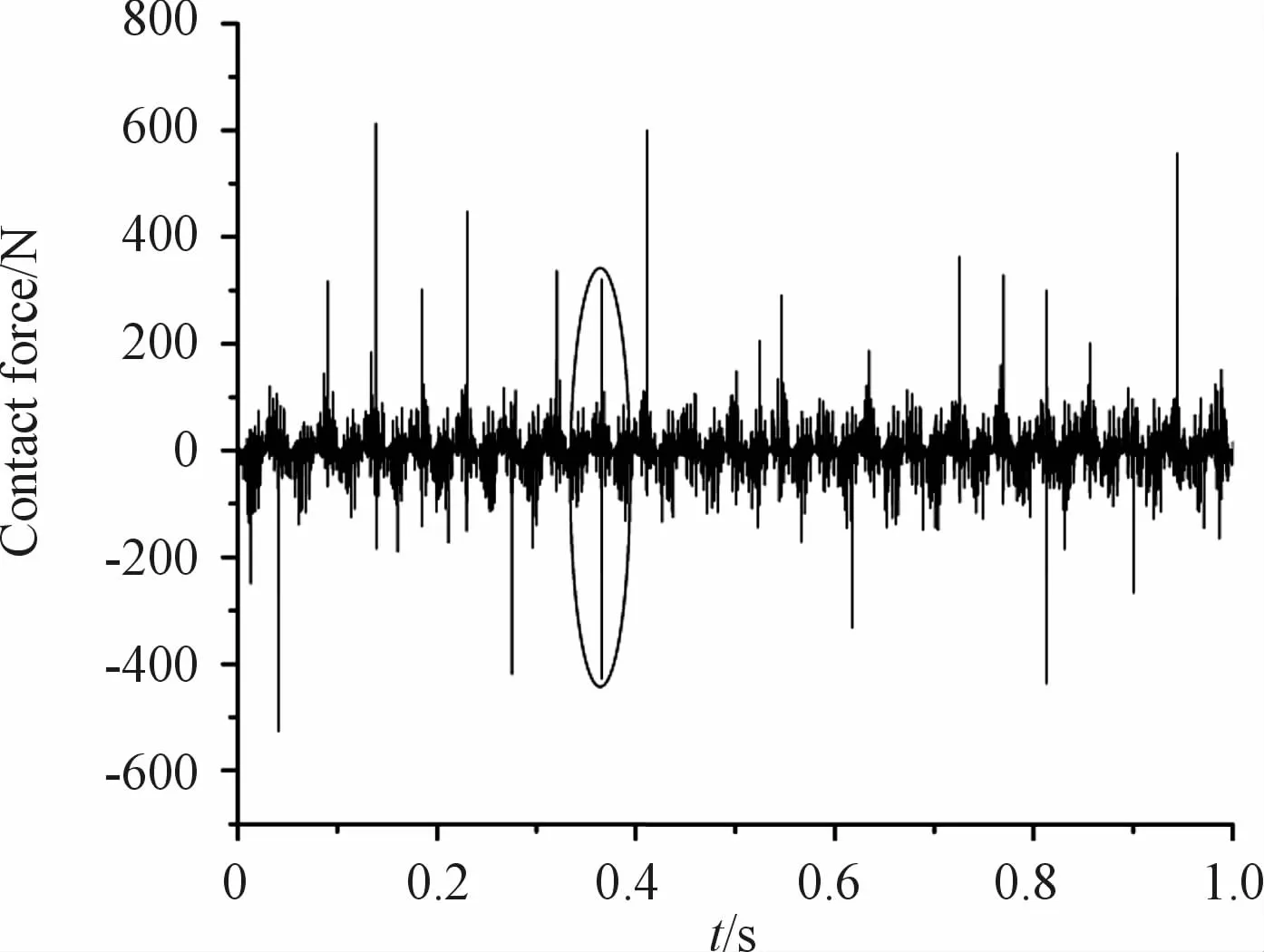
Fig.11 Contact force change diagram of outer ring and roller

Fig.12 Local contact force diagram of outer ring and roller

Fig.13 Vibration displacement diagram of bearing outer ring

4.2 Influence of defect size on bearing vibration

Fig.14 shows the variation of the peak value at the bearing characteristic frequency with the defect length when the width（w）and depth（d）of the circular defect are constant and the defect length is 3 mm，6 mm，9 mm，and 12 mm，respectively.As can be seen from the figure，when the depth and width of the localdefects of the bearing are consistent，the peak value at the characteristic frequency in the bearing spectrum gradually increases with the increase in the defect length，which means that the impact of the rolling body when passing through the local defect increases with the increase in the defect length.

Fig.14 Basic change diagram of vibration amplitude with defect length

Fig.15 is a graph showing the change of the peak value at the outer ring characteristic frequency in the vibration signal spectrum with the increase in the width and depth of the defect of the bearing when the length of the local defect of the bearing is constant.It can be seen from the figure that with the increase in the depth and width of local defects，the peak value of the outer ring fault characteristic frequency in the bearing outer ring vibration signal spectrum gradually increases.

Fig.15 Effect of width and depth of defect on bearing vibration response

4.3 Influence of defect location on bearing vibration

Fig.16 is a graph showing the influence of the position angle of the defect on the variation of the peak value at the characteristic frequency of the bearing outer ring vibration fault under three different types of local defects.The range of position angle of the local defect is 0°～60°，where 0°is the maximum load of the rolling element position.

Fig.16 Diagram of vibration amplitude varying with angle

It can be seen from Fig.16 that，when the position of the local defect of the bearing gradually moves away from the bearing center，the peak value at the characteristic frequency of the outer ring fault characteristic of the bearing outer ring vibration signal spectrum gradually decreases.When the position angle exceeds a certain value，the peaks of the fault characteristic frequency of the vibration signal spectrum diagram of bearings with different types of defects are intertwined with little difference.This can be understood as an increase in the local defect position angle of the outer ring，with the local defect gradually moving away from the bearing area of the bearing，and when the rolling element rolls in or out of the damage pit，the load borne by the rolling body itself is reduced，and the impact caused by it is also reduced.The impact on bearing vibration becomes smaller.

5 Test verification

5.1 Test conditions

In this test，an NF308 cylindrical roller bearing is used as the test bearing.Specific bearing parameters：inner diameter d＝40 mm，outer diameter D＝90 mm，width B＝23 mm，basic dynamic load rating Cr＝76.2 kN，static load C0＝50.2 kN.60CST turbine oil is used as bearing lubricant.Fig.17 is a BVT-5 type bearing vibration measuring instrument，and Fig.18 is a bearing outer ring machined by an electric spark cutting machine.

Fig.17 BVT-5 bearing vibration measuring instrument

Fig.18 Surface defect diagram of bearing raceway

5.2 Test method

The test was completed on a BVT-5 type bearing vibration（speed）measuring instrument.The inner ring of the bearing is fixed on the mandrel of the testing machine to rotate together with the mandrel，while the outer ring is fixed under the action of the bracket.The spindle speed is 1 800 r／min，and the radial load that can be applied is between 150～300 N.So，the test scheme can only be compared with the simulation data under a bearing speed of 1 800 r／min.The specific research methods are as follows：

1）Generate rectangular defects of different sizes on the surface of the bearing outer ring raceway by using the electric spark cutting method；

2）Use 1500-mesh metallographic sandpaper to remove surface residues that may be left on the edges of the defects during processing.

3）Radial load is applied during the test according to the specific test conditions.

4）By adjusting the test conditions such as bearing position and radial loading，the bearing vibration signal is collected using a data acquisition card.The sampling frequency is 1 024 Hz and the number of sampling points is 20 480.Each working condition is repeated three times.The data collected by the data acquisition card is processed by MATLAB and compared with the results of the simulation.

5.3 Test results and analysis

Figs.19 and 20 show the vibration speed signals of normal bearings and damaged bearings and their corresponding spectrum diagrams.Table 4.shows the comparison between the theoretical calculations and the test acquisition signals.

Fig.19 Vibration signal diagram of normal bearing

Fig.20 Vibration signal diagram of damaged bearing

Table 4 Comparison between theoretical calculation and experimental results

It can be seen from the bearing vibration acceleration diagram and the spectrum diagram that when the bearing is defective，the bearing vibration speed and amplitude at the characteristic frequency in the spectrum diagram obviously increase，and the frequency of rotation of the main shaft and the appearance of the characteristic frequency of the bearing outer ring fault can be clearly seen in the spectrum diagram.

Fig.21 shows the change in the vibration signal spectrum of the test bearing outer ring when the position angle of the local defect of the bearing outer ring raceway is changed from 0°to 60°.Among them，the solid line indicates the simulation data，and the dotted line indicates the experimental data.

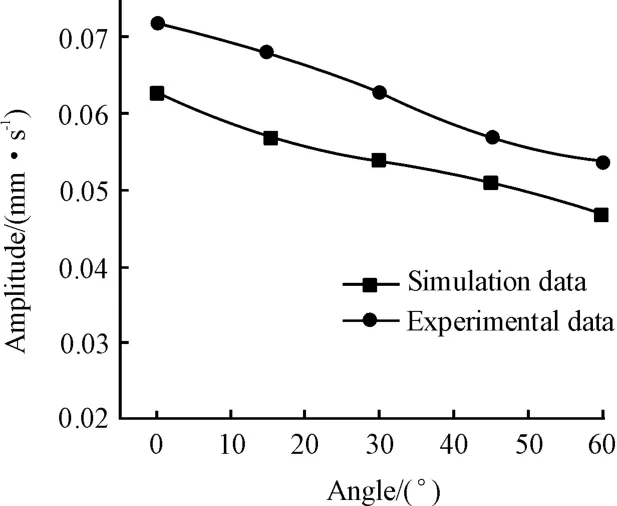
Fig.21 Spectrum change diagram of bearing vibration signal under different radial forces

The comparison between the test and simulation shows that the vibration response of the test bearing gradually decreases with the increase in the local defect position angle.In addition，the test data is slightly larger than the simulation data.The reason is that the signal collected from the test is larger than the actual value due to the influence of the vibration of the testing machine and the self-processing error of the bearing during the test.However，the data trends obtained from the simulation and the test are basically the same，and the errors are relatively small.The simulation results are basically consistent with the test results.

6 Conclusion

In this paper，a multi-body dynamic model is used to study the influence of local defects of the bearing outer ring on the vibration response of bearing dynamic system in time domain and frequency domain.According to the time domain and frequency domain analysis results of the bearing outer ring vibration response，it is shown that the size and shape of local defects will affect the bearing vibration.And when the size of the defects is similar，the change in defect size has little effect on the results of the bearing vibration signal in time domain，but has a great effect on the peak value at fault characteristic frequency in bearing frequency domain analysis.The main conclusions are as follows：

1）With the increase in local defect size，the vibration response of the bearing gradually increases；

2）With the change in the local defect position of the bearing，the vibration response of the bearing gradually decreases when it is away from the bearing area；

3）By comparison，the vibration response of the rectangular defect is the largest，triangular defect the second，and circular defect the smallest.

4）The relationship between the vibration response of cylindrical roller bearing and external load，size and location of local defects was obtained through experiment，and compared with the simulation results to verify the reasonableness of the dynamic analysis.