粗糙表面微凸体对液黏传动的影响*
李 虎 崔建中 孟利民 马如宏
(1.安徽理工大学机械工程学院 安徽淮南 232001;2.盐城工学院机械工程学院 江苏盐城 224002)
液黏调速离合器利用液黏传动技术,在牛顿内摩擦定律的基础上,依靠主、被动摩擦片之间的油膜剪切作用来进行转矩的传递,具有调速灵敏度高、能够实现无极调速、过载保护等特点,能满足一些大功率机电设备的柔性传动要求。因此,被广泛用于风机、水泵等通用设备中,来达到提高传动效率、减少能源消耗的目的。
迄今为止,有大量关于离合器的接合过程的研究[1]。基于改进的平均流量模型和G-T模型,杨夏等人[2]和李阳明等[3]对湿式离合器的接合过程进行动力学建模,分析了摩擦副工作参数对传递转矩的影响。钱灿荣[4]基于分形理论的M-B模型,研究了湿式离合器摩擦力与微凸体接触面积、分形参数之间的作用机制。YAGI等[5]探讨了等效摩擦因数对一组湿式纸基摩擦副传递转矩的影响规律,得到了表面粗糙度与离合器传递转矩间的关系。刘强等人[6]依据G-W模型建立了液黏传递过程中的微凸体接触模型,分析了混合摩擦阶段下摩擦副的摩擦特性。杨辰龙[7]引用KE粗糙接触理论,研究了不同工况参数对离合器结合特性的影响规律。LI等[8-9]通过引入材料接触系数与摩擦副表面形貌参数,对摩擦副的转矩方程进行修正,并通过理论计算与实验结果的对比,验证了修正后模型的正确性。石光林等[10]将摩擦因数引入到赫兹接触理论之中,得到了离合器摩擦副的摩擦因数对接触特性的影响规律。
总结已有研究成果发现:首先,绝大部分关于液黏传动过程中粗糙表面微凸体接触的研究都建立在如G-T模型、G-W模型等统计学模型的基础上,不能反映粗糙表面微凸体的多重尺度特性;其次,针对分形理论中的M-B模型研究只考虑了微凸体的弹性变形与塑性变形,忽略了微凸体的弹塑性变形过程。因此,本文作者以液黏传动过程的微凸体为研究对象,考虑分形理论中微凸体的弹性变形、弹塑性变形及塑性变形3种变形,对液黏调速离合器混合摩擦与边界摩擦阶段下的微凸体承载过程进行分析与建模。
1 微凸体承载模型
1.1 粗糙表面分形特征
与建立在统计学模型基础之上的传统粗糙表面表征方法不同,采用分形参数表征的粗糙表面轮廓曲线具有尺度无关性,即不受限于采样长度等。同时,分形参数也能反映出轮廓曲线的粗糙程度与不规则性,因此 ,在研究一些较为复杂或是不规则的表面时,采用分形参数对表面轮廓曲线进行表征更加合适。
可用W-M函数来生成具有分性特征的粗糙表面轮廓曲线,如图1所示。
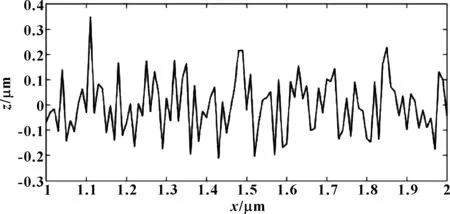
图1 W-M粗糙表面分形轮廓曲线Fig 1 Fractal contour curve of W-M rough surface
W-M函数[11]为
(1)
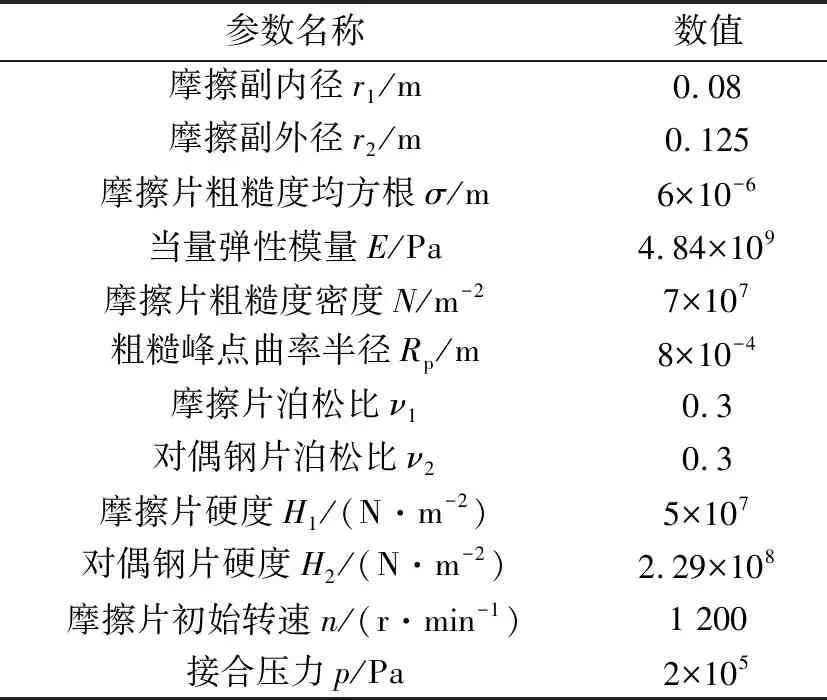
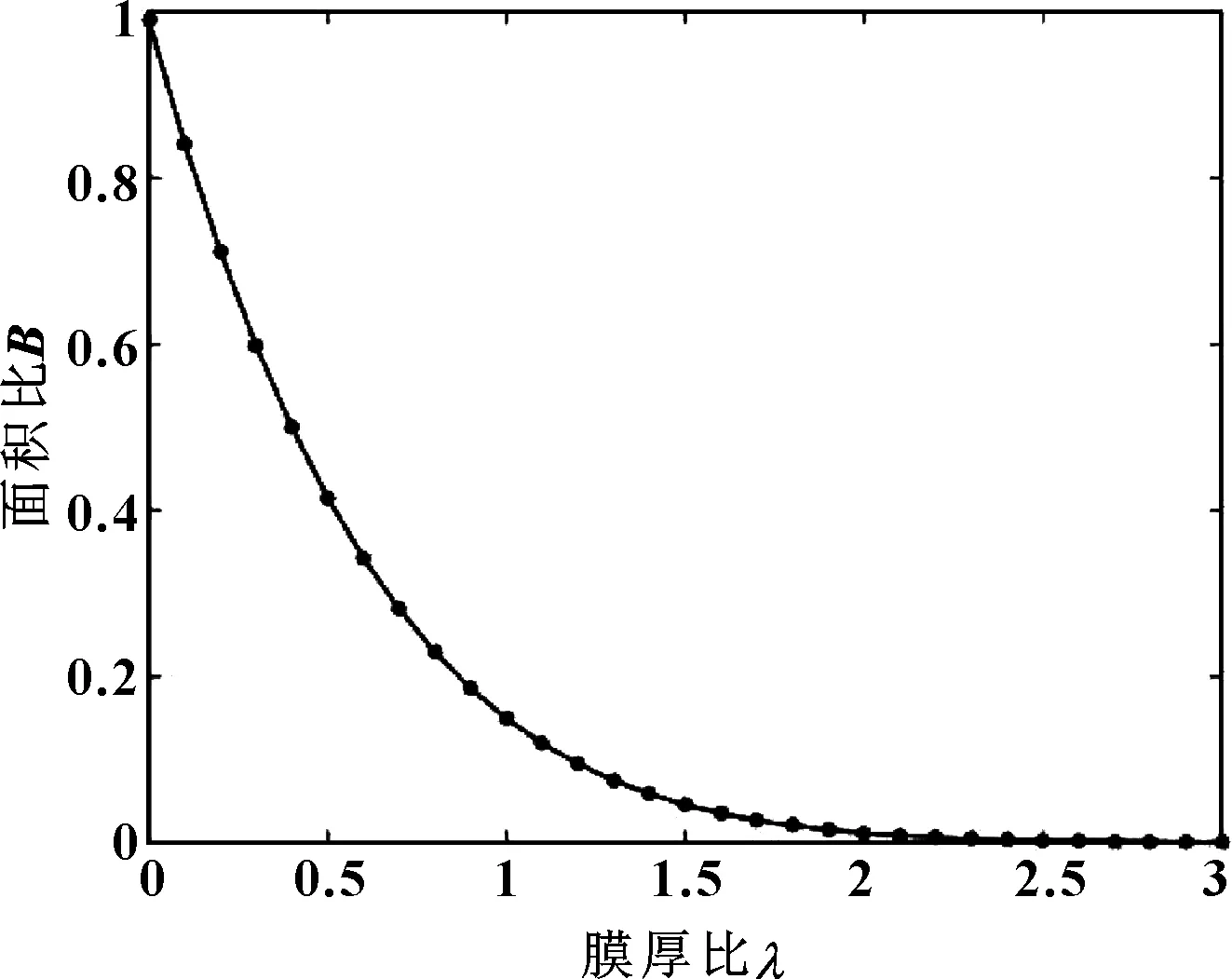
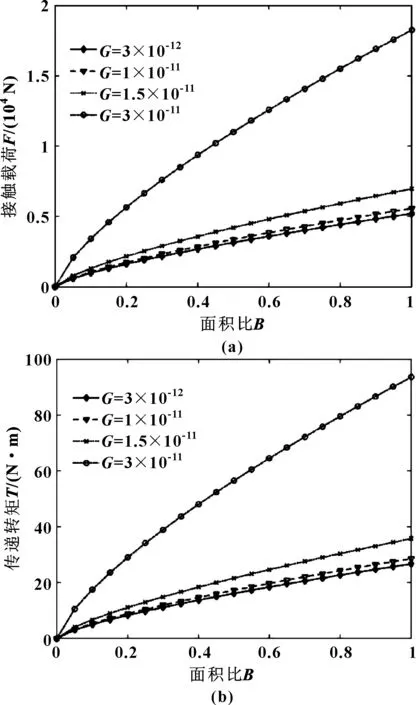
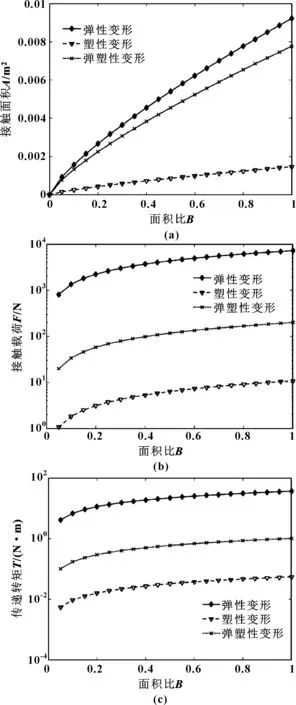
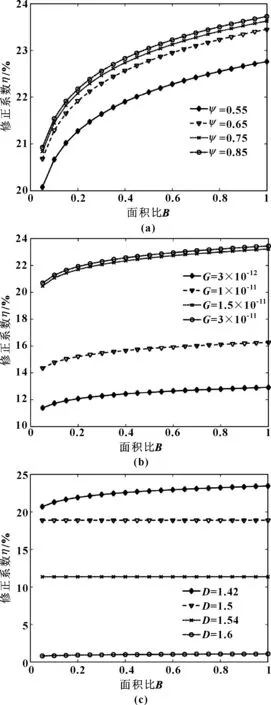
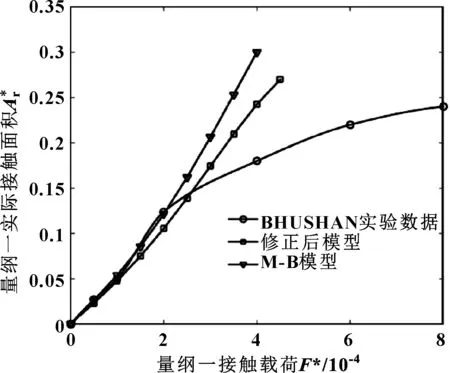
式中:z(x)是随机表面的轮廓高度;x是分形表面位移坐标;G是尺度系数;D是分形维数(1 图2是液黏调速离合器主、被动摩擦片两表面接触变形示意图,将其中一个摩擦片的表面理想为没有微凸体特征的光滑平面。首先分析单个微凸体的变形与受力情况。 图2 粗糙表面与光滑平面示意Fig 2 The schematic of rough surface with smooth surface 当单个微凸体发生变形时,微凸体顶端变形量δ为 δ=G(D-1)a(2-D)/2 (2) 式中:a是接触点的接触面积。 在M-B模型中,微凸体只发生弹性变形与塑性变形,因此,当单个微凸体由弹性变形转变为塑性变形时,微凸体顶端的临界变形量[12]为 (3) (4) (5) 式中:E1、E2分别是主、被动摩擦片摩擦材料的弹性模量;E是两摩擦片材料的当量弹性模量;ν1、ν2分别是主、被动摩擦片摩擦材料的泊松比;H是摩擦材料较软的摩擦片的材料硬度;R是微凸体曲率半径。 由式(2)、式(3)和式(5)可得,此时微凸体的临界接触面积为 (6) 在实际情况中,微凸体弹性变形转变为塑性变形并不是一个突变的过程,在这两种变形之间还存在一个过渡的过程——弹塑性变形。当微凸体从弹性变形转变为弹塑性变形时,微凸体顶端临界变形量[13]为 (7) 式中:K是材料系数,由文献[12]得K=0.454+0.41ν;ν是摩擦材料较软的摩擦片的泊松比。 在弹性变形阶段,由于实际的临界接触面面积为弹性临界面积的1/2,由式(2)、式(5)和式(7)可得,单个微凸体实际的临界接触面积是: (8) 当单个微凸体转变为塑性变形时,微凸体顶端临界变形量约为发生临界弹性变形时微凸体顶端临界变形量的110倍[14],即 (9) 由式(2)、式(5)和式(9)得单个微凸体实际的临界接触面积为 (10) 由M-B模型得:当a≥a1时,微凸体发生弹性变形。根据赫兹理论,此时接触点顶端变形量δ与载荷pe分别为 δ=a/(πR) (11) (12) 由式(5)、式(11)和式(12)得弹性变形时接触点载荷pe为 (13) 当a≤a2时,微凸体发生塑性变形,此时接触点载荷pp为 pp=Ha=Kσya (14) 当a2≤a≤a1时,微凸体处于弹塑性变形状态,此时接触点载荷pep[13]为 (15) 式中:HG为等效弹塑性指数;σy为材料屈服极限。 当一粗糙表面与一平面发生接触时,可用海洋岛屿面积分布函数来表征此时微凸体接触点的面积分布,微凸体接触点的面积分布规律[12]为 (16) 由式(8)、式(10)和式(16)可得,微凸体各变形阶段的实际接触面积分别为 弹性变形: (17) 弹塑性变形: (18) 塑性变形: (19) 因此,在整个接触区域内,实际接触面积为 (20) 假设面积比B定义为实际接触面积Ar与摩擦副总接触面积A的比值,面积比B[15]可表示为 (21) (22) (23) 式中:N是摩擦片粗糙度密度;Rp是微凸峰峰点曲率半径;σ是摩擦片粗糙度均方根;λ是油膜厚度与摩擦片粗糙度均方根的比值即膜厚比;ψ是有效面积系数;r1是摩擦副内径;r2是摩擦副外径;wl是粗糙表面的最低频率,由取样长度决定;wh是粗糙表面的最高频率,由观测仪器的分辨率决定。 在已有M-B模型中,均假设微凸体只发生弹性与塑性变形,因此,接触区域内的总接触载荷F′由弹性接触载荷F′e和塑性接触载荷F′p组成: F′=F′e+F′p (24) (25) (26) 当考虑微凸体的弹塑性变形时,接触区域内的总接触载荷F由弹性接触载荷Fe、弹塑性接触载荷Fep与塑性接触载荷Fp共同承担: F=Fe+Fep+Fp (27) (28) (29) (30) 由式(28)可知,当D=1.5时,Fe分母为0,此时将D=1.5+ξ代入式(28),ξ为一趋近于无穷小的量,由求解精度决定。 当摩擦副间微凸体开始接触后,微凸体和油膜共同承担液黏传动转矩,此时,由微凸体接触而产生的传递转矩[6]为 (31) 式中:f是微凸体摩擦因数,其与接合压力p的关系[16]为 f=0.073-0.155 7p+0.233p2-0.159 5p3+0.037 9p4 (32) 进行仿真分析时所用到的基本参数如表1所示,通过仿真分析并将该模型与原有的M-B模型进行对比,得到了液黏传动过程中有效面积系数、分形维数和尺度系数对微凸体接触的总接触载荷、传递转矩以及两模型修正系数的影响;也获得了微凸体变形过程中各阶段的面积、承受载荷与传递转矩的大小以及弹塑性变形对接触载荷与传递转矩的影响。 表1 基本参数 图3示出了主、被动摩擦片上的面积比B与膜厚比λ的关系。在液黏传动过程中,随着主、被动摩擦片之间油膜厚度的减小,发生接触的微凸体数目逐渐增多,引起实际接触面积的增大。因此,随着膜厚比的减小,面积比逐渐增加。由图可知,当1<λ<3时,液黏调速离合器处于混合摩擦阶段,此时,摩擦片表面的微凸体开始接触,面积比由0逐渐增加;当0<λ<1时,液黏调速离合器处于边界摩擦阶段,摩擦副间的油膜厚度极小,微凸体接触占主导地位,因此,面积比快速增大。 图3 面积比B与膜厚比λ间的关系Fig 3 Relation between area ratio B and film thickness ratio λ 图4描述了当有效面积系数ψ不同时,微凸体的总接触载荷与传递转矩随面积比B的变化规律。当微凸体发生接触后,微凸体的接触载荷以及传递转矩均随面积比的增大而增大。随着传动过程的进行,摩擦副间的油膜厚度逐渐减小导致油膜承担的外部载荷与传递转矩减少,所以,微凸体承担的接触载荷与传递转矩均需增大来平衡外部载荷与传递转矩;当0 当有效面积系数ψ从0.55增大至0.85时,微凸体的总接触载荷及传递转矩均增大。有效面积系数为摩擦片表面去除沟槽的面积与整个摩擦片面积的比值,因此,摩擦副的总接触面积会随着有效面积系数的增大而增大,同时,这也会引起微凸体间实际接触面积的增大,从而使得接触载荷与传递转矩增大。 图4 有效面积系数ψ对接触载荷(a)、传递转矩 (b)的影响(D=1.54,G=1.5×10-11)Fig 4 Influence of effective area coefficient ψ on contact load (a) and transmission torque (b)(D=1.54,G=1.5×10-11) 由图5可知,当其他条件保持固定时,随着尺度系数G的增大,微凸体的接触载荷与传递转矩均呈现显著的增大。尺度系数是与分形表面粗糙程度相关的系数,尺度系数的变化会对分形表面上各微凸体的高度产生影响,摩擦副表面的尺度系数越大,摩擦副表面越粗糙。随着面积比的增大,整个接触区域内弹性变形区域与弹塑性变形区域的面积会增加,而弹性变形区域与弹塑性变形区域能够承担的接触载荷与传递的转矩较大,因此,随着尺度系数的增大,微凸体接触载荷与传递转矩均有较为显著的增大。 图5 尺度系数G对接触载荷(a)、传递转矩 (b)的影响(ψ=0.65,D=1.54)Fig 5 Influence of fractal roughness parameter G on contact load (a) and transmission torque (b)(ψ=0.65,D=1.54) 图6显示了分形维数D对微凸体总接触载荷与传递转矩的影响规律。可看出,分形维数对微凸体接触载荷与传递转矩的影响较为复杂,分形维数的变化改变了随机表面的轮廓曲线复杂程度,从而影响了摩擦副表面的接触特性。当D=1.5时,微凸体的接触载荷与传递转矩最小,并且随面积比的变化最为缓慢;当D>1.5或D<1.5时,随着分形维数的增大,微凸体总接触载荷与传递转矩均增大。 图6 分形维数D对接触载荷(a)、传递转矩 (b)的影响(ψ=0.65,G=1.5×10-11)Fig 6 Influence of fractal dimension D on contact load (a) and transmission torque (b)(ψ=0.65,G=1.5×10-11) 图7示出了在整个接触区域内,微凸体弹性变形区域、弹塑性变形区域以及塑性变形区域的面积、接触载荷与传递转矩随面积比的变化规律。可知,在微凸体接触的过程中,弹性变形区域的面积、接触载荷及传递转矩均占主导地位,其次是弹塑性变形区域,而塑性变形区域的面积、接触载荷及传递转矩最小。这是因为:当微凸体开始接触时,在接触压力的作用下,面积较小的微凸峰率先发生塑性变形,形成了新的面积较大的微凸峰。随着油膜厚度的减小,微凸峰面积逐渐扩大,而面积较大的微凸峰在接触压力的作用下会发生弹性变形与弹塑性变形。因此,在整个接触范围内,弹性变形区域的面积最大,塑性变形区域的面积最小。由于面积较小的微凸峰率先发生塑性变形,此时,微凸体开始承担外部载荷,微凸体的接触载荷较小,并且塑性变形区域的面积也较小,所以塑性变形区域的接触载荷以及传递转矩最小。 图7 微凸体各变形阶段的接触面积(a)、接触载荷(b)与 传递转矩(c)(ψ=0.65,D=1.54,G=1.5×10-11)Fig 7 Contact area (a),contact load (b) and transmission torque (c) of each stage of the asperity deformation (ψ=0.65,D=1.54,G=1.5×10-11) 图8所示是M-B模型与考虑微凸体弹塑性变形后的修正模型得到的微凸体接触载荷与传递转矩的对比。在其他条件相同的情况下,无论是接触载荷还是传递转矩,M-B模型的计算结果均大于修正后模型的计算结果。当使用M-B模型时,由于不考虑微凸体的弹塑性变形,原本发生弹塑性变形的区域大部分被视为塑性变形,小部分被视为弹性变形。当微凸体发生塑性变形时,同等面积上受到的力要大于弹塑性 变形所受到的力,所以当考虑弹塑性变形时,微凸体的总接触载荷与传递转矩均有所下降。 图8 M-B模型与修正后模型计算的接触载荷(a)、传递 转矩(b)对比(ψ=0.65,D=1.54,G=1.5×10-11)Fig 8 Comparison of contact load (a) and transmission torque (b) by M-B model and the modified model (ψ=0.65,D=1.54,G=1.5×10-11) 图9(a)示出了有效面积系数ψ对修正系数的影响。当有效面积系数增大时,摩擦副的总接触面积增大,这使得微凸体的实际接触面积增大,因此,修正系数也随之增大。图9(b)示出了尺度系数G对修正系数的影响。尺度系数的增大改变了分形表面上各微凸体的高度,导致了整个接触区域内弹性变形区域以及弹塑性变形区域的面积的增加;并且,在M-B模型中,原本应该发生弹塑性变形的区域被视为弹性变形以及弹塑性变形,弹性变形与弹塑性变形对粗糙表面承载特性的影响大于塑性变形,因此,随着尺度系数的增大,修正系数也在增大。图9(c)示出了分形维数D对修正系数的影响。分形维数影响粗糙表面的复杂程度,分形维数越大,微凸体越小,粗糙表面越细化,较小的微凸峰易于发生塑性变形,而塑性变形区域承担的接触载荷与传递转矩在微凸体的总接触载荷与传递转矩中所占比例较小,因此,分形维数的增大导致了修正系数的减小。 图9 有效面积系数ψ (a)、尺度系数G (b)与 分形维数D (c)对修正系数η的影响Fig 9 Influence of effective area coefficient ψ (a),fractal roughness G (b),fractal dimension D (c) on correction factor η 图10 修正后模型与实验数据、M-B模型对比分析 (ψ=0.65,D=1.49,G*=10-10)Fig 10 Comparison of the results of the modified model, experimental data and M-B model(ψ=0.65,D=1.49,G*=10-10) (1)在考虑微凸体弹塑性变形的基础上,对M-B模型进行修正,运用修正后的模型建立了液黏调速离合器传动过程中混合摩擦和边界摩擦两阶段下的微凸体承载模型。研究了微凸体的接触载荷与传递转矩随面积比的变化规律。为后续提高液黏调速离合器的传动效率以及减少边界摩擦时间提供了依据。 (2)微凸体的接触载荷与传递转矩均随面积比的增大而增大。适当地增大摩擦片的有效面积系数与尺度系数,能够提高微凸体的接触载荷与传递转矩。当分形维数为1.5时,微凸体的接触载荷与传递转矩最小。 (3)修正后模型的微凸体接触载荷与传递转矩均小于M-B模型的微凸体接触载荷与传递转矩。两模型间修正系数的范围在25%以内,并且随着有效面积系数与尺度系数的增大而增大,随着分形维数的增大而减小。 (4)在整个接触区域内,弹性变形区域的面积、接触载荷与传递转矩均占主导地位,其次是弹塑性变形区域,塑性变形区域的面积、接触载荷与传递转矩最小。1.2 单个微凸体的分形接触
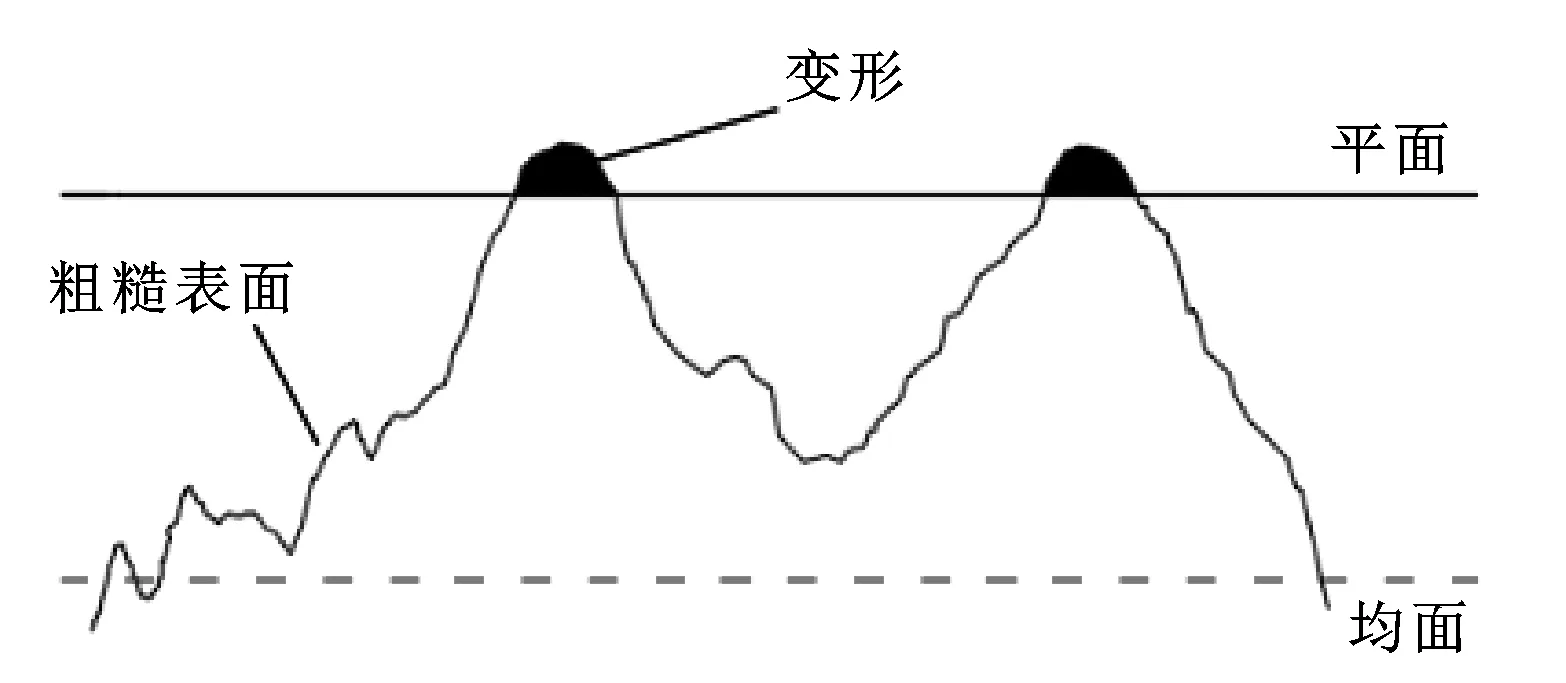
1.3 微凸体实际总接触面积

1.4 微凸体总接触载荷

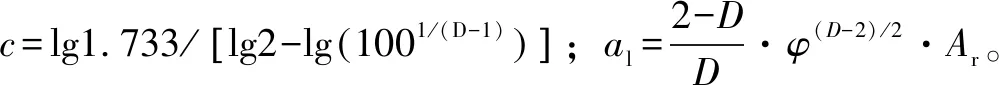
1.5 微凸体总传递转矩
2 数值仿真分析结果及讨论
2.1 有效面积系数的影响

2.2 尺度系数的影响
2.3 分形维数的影响

2.4 弹塑性变形的影响

2.5 与实验数据的比较
3 结论

