基于生本课堂理念的小学数学高阶思维培养

（龙岩市实验小学，福建 龙岩 364000）

所谓“高阶思维”，指的是发生在较高认知水平层次上的心智活动或者认知能力，包含创新能力、问题求解能力、决策力和批判性思维能力。培养学生高阶思维，需要教师遵循生本课堂理念，也就是以学生的发展为本，培养学生独立自主的学习能力，因此，在教学中，应将课堂还给学生，为学生提供分析、探究、延伸、评价的机会。在生本课堂理念下，教师需要在课堂留白，为学生创造自主思考的时间和机会；利用小组合作，激活学生创造性思维；寻求知识间的关联，培养综合求知能力；将评价交给学生，引导学生交流心得，［1］以培养学生的高阶思维。

一、精心设问，培养问题求解能力

在传统的课堂上，教师注重讲授，注重知识的灌输，学生没有思考的时间和机会，只能对教师所传授的知识进行记忆和全盘接受。而在生本课堂理念下，教师不再是课堂的中心，而是成为学生的伙伴，与学生一起组建“学习共同体”，为学生留白，给学生更多思考的时间和空间。［2］通过精心设问，引导学生分析思考，培养问题求解能力，使学生形成解题认知和对问题举一反三的能力。

例题1 用9 个自然数能排成一个横行、竖行、斜行相加和均为15 的魔术方阵（图1），那么你能找出9个连续的自然数，排成一个横行、竖行、斜行相加和均为18 的方阵吗？请填写图2。

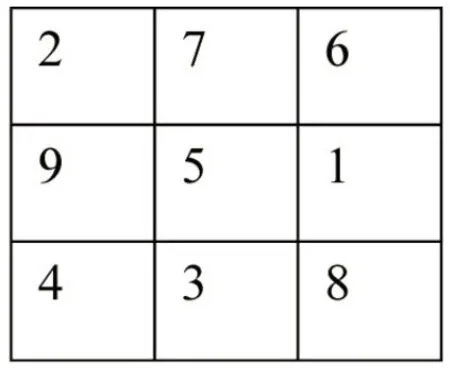
图1

图2

如果图2 中已知几个数字，求出其他数字相对比较简单；但是在完全空白的图中填入9 个数字，使其横行、竖行、斜行相加和均为18，则具有一定的难度。针对这类题型，教师可以给学生做拓展，不是直接教给思路，而是引导学生思考其中的规律和解题方法。比如，以口诀的方法揭示其中的规律：“二、四为肩，六、八为足。上九下一，左七右三。”另外，还有口诀：“一居上行正中央，依次斜填切莫忘；上出框时向下放，右出框时向左放；排重便在下格填，右上排重一个样。”通过设问并分析问题，提升学生的问题求解能力，有利于学生自主学习和解决问题，培养高阶思维能力。

二、合作学习，激发创造性思维

创造性思维，是一种具有开创意义的思维活动，即开拓人类认识新领域、开创人类认识新成果的思维活动，是高阶思维的一种体现。在培养学生创造性思维的过程中，可利用合作学习这一方式。在生本课堂理念下，教师积极组织小组合作学习活动，提前计划合作学习的时间、地点、人数、活动内容、分工等，在合作中及时巡视、发现问题，引发学生的创造性思维。以《梯形的面积》教学为例，设计以下几个环节：

1.梯度问题，合作突破难点。将学生在学习过程中所呈现出的难点作为合作的主题，为学生设置问题，问题要有一定的思维梯度，使学生能够进行创造性的思考。例如，在教学《梯形的面积》时，教师没有直接引入面积公式，而是提出问题：如何推导梯形的面积公式？然后让学生小组合作探究，在组内交流、讨论。

2.自主思考，形成独到看法。小组合作学习要在学生独立思考分析的基础上展开讨论。教师要鼓励学生大胆剖析问题，明确自己的思路，再与同组同学进行讨论。在小组合作推导梯形面积公式时，每个学生都有独特的设想，教师可要求学生先自己观察梯形，思考如何推导。［3］有的学生将梯形转化为三角形和平行四边形（图3），也有的将梯形转化为平行四边形（图4）。

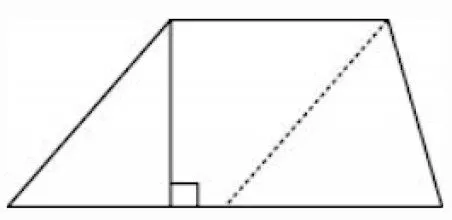
图3

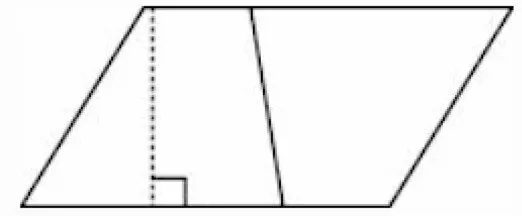
图4

3.思维碰撞，构建知识体系。对于某一个问题，学生经过一定的思考后获得认识，这些认识可能是片面的，也可能是错误的。在小组内讨论和交流，是一个思维逐渐丰富、多元的过程。倾听他人的思路，对比自己的思考，在交流中碰撞出火花，能够激活高阶思维，形成相对完善的解答，逐渐构建知识体系。

三、对比关联，提升综合求知能力

知识之间是相互关联的。培养学生高阶思维，必须让学生寻找知识的脉络、来源和走向，提升学生综合求知能力，调动知识储备进行对比联想，延伸知识与邻近区域的应用，寻找解决问题的最佳路径。

例题2 李伯伯想要用20 根1 米长的木条围成一个长方形的栅栏用来种花，如何才能使他围成的栅栏面积最大呢？

解题思路通常分成三种：如何围？能够围成几种栅栏？最大的是哪一种？确立这三个解题步骤之后，引导学生寻找相关的知识脉络：这道题用到哪些知识点？学生联系到长方形的长、宽、周长、面积等内容。这道题本质上是已知长方形周长求面积的题目，学生通过对比联想，进行综合考虑，最终确立解决方案（见表1）。

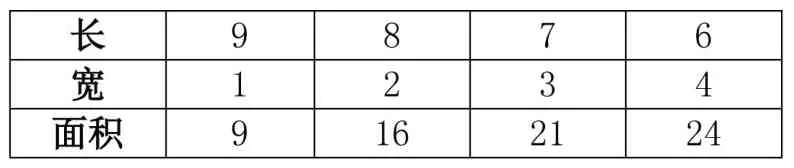
表1

由例题2 可知，长方形的周长：（长+宽）x2=20 米，因此长+宽=10 米，据此可列表格（见表2）：

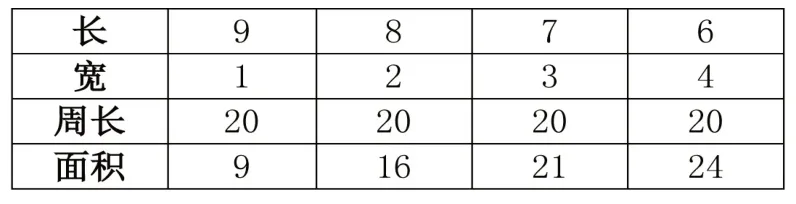
表2

由此可见，围成的长方形的长与宽越接近，它的面积就越大。学生通过对案例的了解，对长方形长、宽、周长、面积等的对照，进行对比关联，提升综合求知能力。

四、评价、反思，发展批判性思维

批判性思维是通过一定的标准评价思维，进而改善思维，是合理的、反思性的思维。在课堂评价过程中，对于一些问题，教师不必急于评价，而是引导学生反思、质疑，让学生之间就合作的内容、学习的情况、答案和解题思路等进行评价。在评价中，学生回顾所学内容，反思解题思路，通过对他人的评价，不断反思自己的问题所在，以发展批判性思维能力。

例题3

140－50

140－75

140－32.5

140－x

问：x 在这里可以表示几？

生1：x 可以表示自然数。

教师并没有急于回答，而是让其他学生对这个答案进行评价和质疑。

生2：x 必须要小于140。

生3：x 不只是小于140 的自然数，因为有个140-32.5，所以x 也可以是小数。

师：那么应该怎样说？

生：140 以内的所有数。

学生一开始并没有给出最准确的答案，教师没有急于点评，而是把评价权交给学生，让学生思考答案的准确性。学生经过不断补充、完善后，得到最终的答案。完成这道题后，引导学生探讨：再次遇到这类题型时，应该如何解答才能确保准确？让学生交流、补充，有利于今后的解题思路更加明晰。