基于一题多解的数学建模教学——以人教版第十一册第六单元“浓度问题”为例

（厦门大学附属实验小学，福建 漳州 363123）

数学模型一般是指对特定的问题用数学语言、符号或图形等形式来刻画、描述、反映的数学结构。数学模型有效地反映了思维的过程，是将思维过程用语言符号外化的结果，学生对数学模型的理解、把握与建构的能力，在很大程度上反映了其数学思维能力及数学观念。一题多解是在解决一道题时，从不同思维角度、方法和知识模块入手，通过解题过程，让学生体会不同知识点的交汇和融会贯通，从本质上看是把数学模块系统化、连贯化、整体化。教师要引导学生多角度思考、解决问题，渗透模型思想，训练模型思维，让学生在触类旁通的过程中建立不同的解题模型。

一、寻求等量关系，建立解题模型

《义务教育数学课程标准（2011 年版）》指出：“模型思想的建立，是学生体会和理解数学与外部世界联系的基本途径，建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果，并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识。”数学模型思想所体现的过程，就是在具体情境中，抽象出数学问题，分析和解决问题的过程。［1］教学中，要针对具体问题，联系生活实际，进行必要的信息分析，合理的简化，在反复提炼中建构数学模型。

以人教版第十一册第六单元百分数中的“浓度问题”为例，“把含盐量30%与5%的盐水混合，得到20%的盐水4 千克，求这两种浓度的盐水分别是多少千克？”学生分析数量关系，简化出解决问题的关键信息：总盐量不变，即第一种盐水中盐的质量+第二种盐水中盐的质量=混合后盐的总质量。引导学生运用学过的方程，用这个基本模型解决此类问题：设其中一个量为x，则另一个量为（4-x），列出的方程为30%x+5%（4-x）=4×20%。解方程后，反思：“解法对吗？符合题意吗？该解法的优缺点在哪里？能够推广吗？还有其他解法吗？”学生的模型思维能力得到强化和提高。此类浓度问题的实质是溶质质量相等，大致的解题思路就是抓住溶液质量与百分比的乘积等于溶质质量这一原理，再通过等量关系列出方程。让学生经历寻找实际问题中数量之间的相等关系，正确列出等量关系式，整个解题过程条理清晰，同一类型问题解题模型的建立也就水到渠成了。

二、整合新旧知识，体会模型应用

整合新旧知识并进行类比推理时，重在沟通新旧知识间的联系。先大胆猜想，再在直观的事例中具体分析，不断联系所要解决的问题和已有的知识结构，引导学生将之前所掌握的解题方法迁移到新的问题解决中来，建立新的解题模型。在观察、比较中区分问题属性的异同，并找出它们类似的特征，从而加深对新解法的理解。［2］

上述浓度问题，学生在尝试运用算术解法解答时遇到困难，教师可引导学生观察方程解法中解方程的过程，设疑唤醒学生原有的知识：浓度5%的盐水不是4 千克，为什么解方程过程中出现了4×5%？在解决哪类问题时，运用到了哪种方法？你有什么猜想？学生在猜想是否把4 千克盐水看成都是浓度5%的盐水的过程中，联想到“鸡兔同笼”问题中的“假设法”，用假设法解释浓度问题，将模型思想方法与自己以往的知识相联系，将两种问题整合在同一解题模型中。

假设混合后的4 千克盐水浓度都是5%，那么应该有盐：4×5%=0.2（千克），实际有（4×20%=0.8）千克的盐，比实际少算了：0.8-0.2=0.6（千克）。这是因为学生把浓度30%的盐水都看成了浓度5%的盐水，也就是浓度30%的盐水每千克盐水中所含的盐的百分比少算了25%，正好多了0.6 千克。运用对应数量÷对应分率，可以得到含盐量30%的盐水质量，列式为：0.6÷（30%-5%）=2.4（千克），则浓度为5%的盐水有：4-2.4=1.6（千克）。学生联系“鸡兔同笼”问题中的“列表法”，尝试同相同方法解决浓度问题（见表1）。

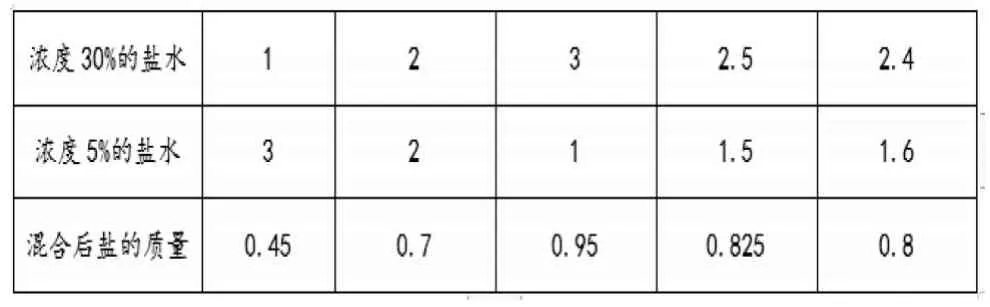
表1

从表1 中可以看出，每调整1 千克的溶液，溶质相差（0.7-0.45）千克，混合后盐的质量是0.8 千克，比0.7千克多了0.1 千克，所以还需要调整0.1÷（0.7-0.45）=0.4（千克），2+0.4=2.4（千克）。

对比列表法在“鸡兔同笼”问题中的运用，学生发现：鸡和兔的只数都是整数，用列表法较容易算出总只数；浓度问题中的盐水质量可能是小数，调整时要考虑到小数因素，需要推导出每次调整引起的数据变化，结合计算得出最后的结论。学生在新旧知识的整合中明确解题思路，在转化的过程中化“生”为“熟”，化难为易，运用假设的数学思想方法，归纳出解题模型：较大浓度盐水=（盐的总质量-溶液总质量×较小浓度）÷浓度差；较小浓度盐水=（溶液总质量×较大浓度-盐的总质量）÷浓度差；在运用列表的数学方法中存同求异，体会模型的变化，建立相应的解题结构。

三、联想创新，重构新模型

对一个问题多角度的理解，能训练学生思维的广阔性和灵活性。同样是一道习题，一个知识点，不同的理念，不同的方法，会有不同的效率和价值。［3］在一定的简化层次下，很多看起来完全不同的实际问题，可能有相同或相似的数学模型。此时，如果能引导学生展开联想，启发学生提出新思路、新设想，充分挖掘学生的创新思维能力，在创新过程中实现新的解题建模，则有利于推动学生思维的发展。

例如，学生结合课外学习所得，用图示介绍解决混合浓度问题的另一种方法——十字交叉法：先写出混合前的两种浓度和混合后的浓度，交叉算出混合前与混合后的浓度差，再算出两个浓度差的比值，最后把总质量根据这个比值按比例分配求出原来两种盐水的质量（如图1）。

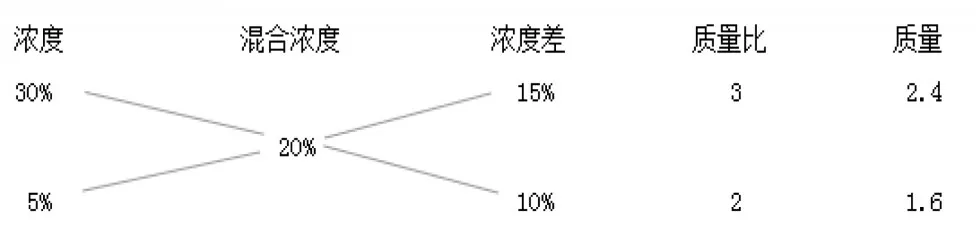
图1

在理解“十字交叉法”解题模型的过程中，学生不知道为什么交叉的浓度差的比就是两种盐水的质量比，教师引导学生采用假设法说明理由：假设两种盐水的浓度都是20%，则第一种盐水中多了10%的盐，这10%的盐要补到第二种盐水中，所对应的就是第二种盐水的质量，所以才要交叉求出浓度差。学生联想到用比例解决问题，创造出比例解题模型：

先分别求出浓度差：

30%-20%=10% 20%-5%=15%

再交叉算出浓度差的比：15%：10%=3：2

最后按比例分配分别算出两种溶液：

在本环节模型思维拓展的过程中，教师注重引导学生发现知识、问题与方法的关联性，归纳外在特点和内在联系，调整知识结构，促使学生创新实践，学生在理解解题模型的过程中，发现数量中的对应关系，创造出新的解题模型。当学生对具体的生活问题经历了一定的探索过程之后，便会发现数量之间的关系，生活问题便转化为数学问题，综合性地用数学模型解决问题，形成不同的解题策略。