正交各向异性钛制圆柱壳接管结构临界失稳压力研究
张晋武,贺小华
(南京工业大学 机械与动力工程学院,南京 211816)
0 引言
钛是一种典型的正交各向异性材料,其具有抗腐蚀、低密度、比强度高等优良的材料性能,在航空航天、军事、深海工程及压力容器等领域有着广泛的应用。包括JB/T 4745—2002《钛制焊接容器》、GB/T 150—2011《压力容器》等在内的国内外标准,依旧是将钛材作为各向同性材料进行处理,虽然这种处理方式在实际工程应用中具有较大的便利性,但也会因其产生一些误差和不确定性。
外压容器在石油化工、压力容器等领域有着普遍的应用,圆柱壳接管结构是其最常见的结构之一。失稳是外压容器失效的主要形式,临界失稳压力则是外压容器稳定性研究的重要参数。文献[1]基于经典Levy-Timoshenko法,考虑材料弹-塑性及几何缺陷等因素,对外压薄壁圆柱壳与圆环的临界压力公式进行了改进;文献[2]基于正交试验设计方法,对外压圆柱壳接管结构临界失稳压力进行有限元模拟,进一步通过多因素方差分析得到各结构参数的显著度;文献[3]基于有限元非线性分析,对外压圆柱壳接管结构的稳定性作了系统性研究,得到了各结构参数对临界失稳压力的影响规律;文献[4]将碳纤维复合材料作为各向异性材料,通过采用有限元模拟、试验验证和理论公式对碳纤维复合材料圆筒的稳定性进行分析,验证了有限元模拟的准确可靠性。文献[5]从壳体稳定性基本理论出发,推导了适合工程计算的正交各向异性壳体的临界外压公式;文献[6]采用有限元数值模拟,对正交各向异性锥壳稳定性进行了系统性研究,结果表明正交各向异性锥壳临界失稳压力变化规律与各向同性锥壳基本相同,相同参数下,正交各向异性锥壳临界失稳压力普遍高于各向同性锥壳15%~23%。
本文对正交各向异性钛制圆柱壳接管结构临界失稳压力进行有限元非线性分析,比较正交各向异性与各向同性圆柱壳接管结构临界失稳压力,探讨各结构参数对正交各向异性圆柱壳接管结构临界失稳压力的影响;进一步对正交各向异性钛制圆柱壳接管结构临界失稳压力进行回归分析,得到回归方程,为正交各向异性钛制圆柱壳接管结构外压稳定性研究及工程应用提供借鉴。
1 有限元分析与计算方案
基于有限元软件ANSYS,采用几何-材料非线性的屈曲分析方法,对钛制圆柱壳径向开孔接管结构(简称圆柱壳接管)进行数值模拟,以得到载荷-位移曲线,采用双切线准则获得其临界失稳压力,进而对其稳定性进行系统研究。
1.1 TA2正交各向异性材料参数
圆柱壳接管结构材料为工业纯钛TA2[7],通过MTS880材料试验机、DRA-107A应变仪等实验器械测定以及小冲孔试验[8-10],获得TA2各向异性材料力学性能参数[11-12],如表1所示。表1中,r为板材厚度方向,θ为板材宽度方向,z为板材轧制方向。根据文献[6]中研究结果,取母线方向与轧制方向一致,可以获得最优的承载能力。

表1 TA2材料参数
1.2 有限元计算方案
针对圆柱壳接管结构,保持筒体壁厚δe不变,其值为10 mm,通过改变其他4个无量纲参数(径厚比D/δe、接管与筒体厚度比δet/δe、开孔率ρ、长径比L/D)建立模型进行数值模拟。计算模型结构参数如表2所示,采用全因素分析方法,正交各向异性和各向同性模型各为144个。

表2 有限元模型结构参数
1.3 单元类型与边界条件
有限元模拟中,选用Shell 181壳单元,其计算精度已在文献[6]中得到证实。筒体两端采用简支约束,即在柱坐标系下,筒体一端约束环向位移,另一端约束环向和轴向位移,接管端面约束环向位移。由于模型结构、约束条件以及所施加载荷均为对称,分析模型建立1/2对称结构,施加对称约束。
2 正交各向异性与各向同性外压圆柱壳及开孔接管结构临界失稳压力
由于加工制造、运输等众多因素,壳体不可避免会产生初始几何缺陷[13]。因此,在ANSYS非线性数值模拟中,基于“一致缺陷模态法”[14],对模型施加10%厚度的初始几何偏差。通过时间历程后处理器提取模拟结果中位移最大点的载荷-位移曲线,根据双切线准则[15]获得相应的临界失稳压力。各向同性圆柱壳及开孔接管结构计算模型中,材料性能取轧制方向数据;各向异性材料的力学性能依照表1中数据设置。
2.1 圆柱壳结构临界失稳压力
为比较正交各向异性与各向同性圆柱壳临界失稳压力,引入比值系数K1(正交各向异性与各向同性圆柱壳临界失稳压力之比)。不同径厚比D/δe、长径比L/D下,外压圆柱壳的临界失稳压力Pcr以及比值系数K1如图1(图中,iso表示各向同性材料,orth表示正交各向异性材料)所示。

图1 圆柱壳结构临界失稳压力Pcr及比值K1
由图1可以看出,正交各向异性与各向同性圆柱壳的临界失稳压力Pcr变化规律基本相同。相同参数下,正交各向异性圆柱壳临界失稳压力Pcr均大于各向同性圆柱壳。当L/D=2.5时(短圆筒),K1=1.107~1.122;当L/D=Lcr/D时(临界长度圆筒),K1=1.093~1.102;当L/D=30时(长圆筒),K1=1.08~1.087。随着长径比L/D的增大,正交各向异性材料对圆柱壳外压稳定性的增强效应有所降低。
2.2 圆柱壳接管结构临界失稳压力
为比较正交各向异性与各向同性圆柱壳接管结构临界失稳压力,引入比值系数K2(正交各向异性与各向同性圆柱壳接管结构临界失稳压力之比)。不同结构参数下圆柱壳接管结构临界失稳压力Pcr以及比值K2如图2~5所示。
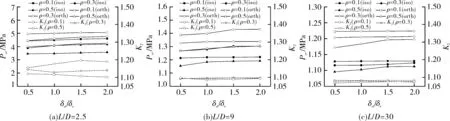
图2 圆柱壳接管结构临界失稳压力Pcr及比值K2(D/δe=60)
由图2~5可以看出,相同参数下,正交各向异性圆柱壳接管结构临界失稳压力均大于各向同性圆柱壳接管结构,比值系数K2皆大于1,其最大值为1.195 4。当L/D=2.5时,K2=1.076~1.195 4;当L/D=Lcr/D时,K2=1.085 6~1.114 3;当L/D=30时,K2=1.069 2~1.108 3。随着长径比的增大,正交各向异性材料对圆柱壳接管结构外压稳定性增强效应有所降低。

图3 圆柱壳接管结构临界失稳压力Pcr及比值K2(D/δe=80)

图4 圆柱壳接管结构临界失稳压力Pcr及比值K2(D/δe=150)

图5 圆柱壳接管结构临界失稳压力Pcr及比值K2(D/δe=200)
正交各向异性与各向同性圆柱壳接管结构临界失稳压力Pcr与结构参数的变化规律基本相同。临界失稳压力Pcr随径厚比D/δe增大显著减小;临界失稳压力Pcr随长径比L/D增大显著降低,至临界长径比后无显著下降;临界失稳压力Pcr随开孔率ρ增大逐渐下降,D/δe或L/D越小,ρ对Pcr的影响程度越显著;临界失稳压力Pcr随厚度比δet/δe增大逐渐增大,但δet/δe的增大对Pcr的增强作用较为有限,当ρ较小时,δet/δe对Pcr的增强效应较小;随着ρ的增大,δet/δe对Pcr的增强效应随之增大。
3 正交各向异性圆柱壳接管结构与正交各向异性圆柱壳临界失稳压力的比较
为探讨正交各向异性材料开孔接管对圆柱壳的影响,引入比值系数K3(正交各向异性圆柱壳接管结构与正交各向异性圆柱壳临界失稳压力之比)。图6~9示出了K3与各结构参数之间的关系,以下讨论各结构参数对K3的影响规律。
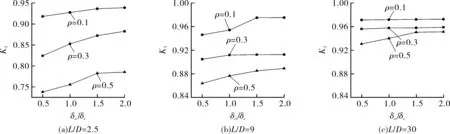
图6 圆柱壳接管结构与圆柱壳结构临界失稳压力比值K3(D/δe=60)

图7 圆柱壳接管结构与圆柱壳结构临界失稳压力比值K3(D/δe=80)

图8 圆柱壳接管结构与圆柱壳结构临界失稳压力比值K3(D/δe=150)

图9 圆柱壳接管结构与圆柱壳结构临界失稳压力比值K3(D/δe=200)
对于开孔率ρ,当ρ=0.1时,K3=0.917 9~1.002 7;当ρ=0.3时,K3=0.824 1~0.995 9;当ρ=0.5时,K3=0.738 0~0.980 0。表明在小开孔(ρ=0.1)下,开孔接管对筒体结构Pcr无明显的削弱;随着ρ的增大,削弱系数K3逐渐降低。不同结构参数下,开孔率ρ对K3的影响程度有所差异。由图6~9可以看出,随着δet/δe,D/δe,L/D的减小,开孔率ρ对圆柱壳Pcr的削弱效应随之增大。本文计算参数范围内,当ρ=0.5,D/δe=60,L/D=2.5,δet/δe=0.5时,K3最小达到0.738 0。在文献[3]中,相同结构参数下,此比值为0.501 1,由此表明,相比于各向同性材料,正交各向异性材料开孔接管对圆柱壳临界失稳压力的削弱有所降低。对于接管厚度比δet/δe,相同参数下,K3随着δet/δe的增大逐渐增大;随着ρ的增大,δet/δe对K3的影响逐渐增强,当δet/δe增至1.5及2.0时,K3变化趋于缓慢,也即当接管厚度比增至一定值后,接管对筒体失稳临界压力的增强效应不再明显。
对于径厚比D/δe,相同参数下,K3随着D/δe的增大逐渐增大;对于长径比L/D,相同参数下,K3随着L/D的增大逐渐增大,至临界长径比后变化不显著;随着D/δe增大,L/D对K3的影响有所降低。
4 正交各向异性圆柱壳接管结构临界失稳压力回归分析
4.1 回归方程模型的确定
上节分析可知,外压作用下的圆柱壳接管结构,结构参数D/δe,L/D,ρ和δet/δe均对临界失稳压力Pcr有不同程度的影响。通过对试验数据进行多因素方差分析,各因素对临界失稳压力影响由大到小依次为:D/δe,L/D,ρ,δet/δe,与文献[2]一致。D/δe与L/D是其主要影响因素,因此,为了方便实际工程应用,基于JB/T 4745—2002《钛制焊接容器》的外压圆柱壳临界压力图算法,将正交各向异性钛制圆柱壳接管结构临界失稳压力的回归公式定为:

式中 f(ρ,δet/δe)——关于开孔结构参数ρ与δet/δe的函数;
Pcrs——基于JB/T 4745—2002计算得到的钛制各向同性圆柱壳临界失稳压力(取安全系数为3.0),MPa。
运用Origin软件对本文有限元数值模拟结果进行回归分析,经过多种回归模型精度比较,最终所选取的回归模型如式(2)所示。

式中 Z0,B,C,D,E,F——系数。
4.2 Origin回归分析结果
根据式(2)的回归模型,得到回归方程如下:

由于系数B数量级比之其他参数过小,可省略,即简化为:

进一步改写为:
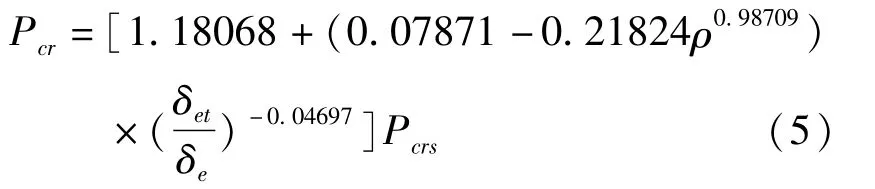
式中,60≤D/δe≤200,2.5≤LD/≤30,0.1≤ρ≤0.5,0.5≤δet/δe≤2.0。
4.3 回归方程的验证
通过将回归方程计算得到的所有模型临界失稳压力与本文有限元数值模拟结果相比较,最大误差为±15%,最小误差为0.04%,平均误差为8.35%。为减小篇幅,选取L16(42×32)正交试验中的16个模型,其误差结果如表3所示,误差结果在工程可接受范围内。
为进一步验证回归方程的准确性和适用性,另选取3组本文未计算的有限元模型,分别为短圆筒(L/D=4)、临界长度圆筒(L/D=15)、长圆筒(L/D=20)。模型结构参数及计算结果如表4所示,最大误差5.89%,结果表明,前文拟合的回归方程(公式(5))可靠、准确。

表3 公式(5)临界失稳压力解与有限元解的比较(1)

表4 公式(5)临界失稳压力解与有限元解的比较(2)
5 结论
采用有限元非线性分析方法,针对正交各向异性钛制圆柱壳接管结构,探讨不同结构参数对其临界失稳压力的影响,并分别与各向同性圆柱壳接管结构、正交各向异性圆柱壳结构进行比较。得到以下结论。
(1)钛制圆柱壳及开孔接管结构,正交各向异性材料临界失稳压力变化规律与各向同性材料基本相同,且各向异性材料临界失稳压力普遍高于各向同性材料约8%~19%,随着长径比的增大,正交各向异性材料对圆柱壳及圆柱壳接管结构外压稳定性增强效应逐渐降低,研究结果为正交各向异性钛制外压容器的轻量化设计提供理论依据。
(2)开孔接管结构对正交各向异性圆柱壳的外压稳定性具有削弱作用,各结构参数对临界失稳压力削弱系数K3具有不同的影响程度。随着δet/δe,D/δe,L/D的减小,开孔率ρ对圆柱壳Pcr的削弱效应随之增大,本文计算参数范围内,临界失稳压力最大削弱系数为0.738 0。相较于各向同性材料,正交各向异性材料开孔接管对圆柱壳临界失稳压力的削弱有所降低。
(3)对正交各向异性钛制圆柱壳接管结构临界失稳压力进行了非线性回归分析,得到其临界失稳压力回归方程,为工程实际应用提供参考。

