铁路隧道救援站通风优化设计研究

黄超，余朝阳

（川藏铁路有限公司，四川 成都610045）

0 引言

我国铁路尤其是高速铁路正在快速发展，铁路建设过程中长大隧道的规模与数量也大幅度增加。众所周知，隧道内空间狭小且密闭，列车内更是人员密集地，而动车组的窗户基本无法快速直接打开，一旦发生火灾危险性更大［1-3］。隧道内发生火灾后急需进行通风，目前隧道的通风设计计算多采用二维通风网络计算，仅考虑了线性问题，未考虑风流过程中空间在横断面上对风速形成的影响。因此，以某单洞双线隧道救援站为例，探讨通过利用二维通风网络计算结果以及三维数值模拟计算对二维通风网络线性结果进行验证，为隧道结构通风优化设计提供建议。

1 工程概况

某隧道为单洞双线隧道，全长约23 km，根据规范要求隧道内设计了救援站。为实现防灾救援，在该段隧道左右两侧各设置1条辅助导坑，同时设置横通道用于连接正洞和辅助导坑，左右两侧各设置11条，间隔50 m。救援站左侧救援通道直接与通向隧道外的辅助导坑相连，右侧救援通道利用新建下穿正洞的联络通道与辅助导坑相连。救援站范围隧道正洞拱部上方设置排烟平导，排烟平导通过正洞拱顶的竖井与正洞相接，竖井间距约为100 m，共设置6个，最终排烟平导通过约500 m长的排烟斜井接出洞外。救援站布置见图1。

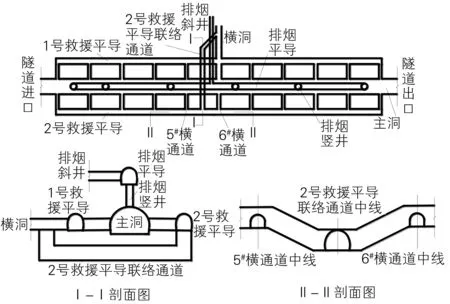
图1 救援站布置示意图

2 模拟计算

假设右线行驶的列车在隧道内发生火灾，并停靠在救援站右侧，根据《铁路隧道防灾疏散救援工程设计规范》［4］要求，在隧道救援站内发生火灾后根据列车行进方向开启对应一侧的救援疏散通道，同时对隧道内进行通风排烟，并保证每道防护门风速不低于2 m/s。

2.1 二维通风网络计算

为满足要求，利用二维通风网络程序经过多次试算得出隧道主洞、横洞的需风量与排烟斜井的排风量（试算时未考虑自然风），计算结果所得边界条件见图2［5］：隧道进口方向送风风速为0.17 m/s、出口方向送风风速为0.18 m/s、横洞送风风速为8.24 m/s、排烟斜井抽风风速为6.29 m/s。

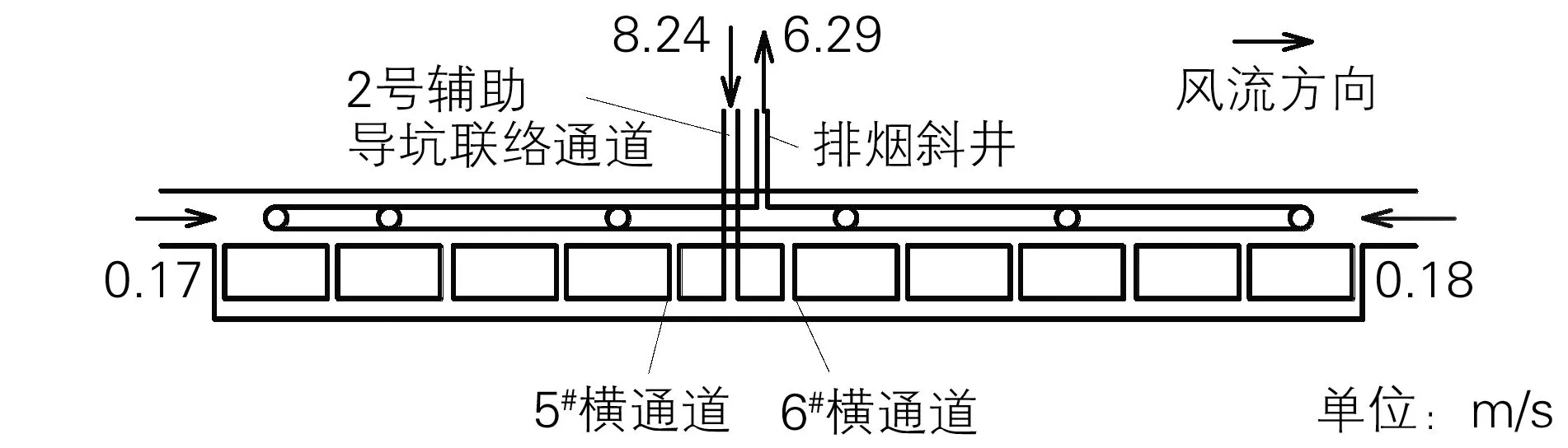
图2 通风网络程序计算所需风速

2.2 三维数值模拟计算

2.2.1 三维数值模拟条件

三维数值计算利用火灾数值模拟软件FDS（Fire Dynamics Simulation）对隧道火灾进行动态模拟。FDS中默认的燃烧模型为混合分数（mixture fraction）燃烧模式；FDS对于辐射换热过程，使用类似于有限体积的方法求解非散射灰体辐射换热方程［3］。

NIST开展了系统实验来验证FDS的火灾模拟预测能力。所有全尺寸试验结果均表明FDS在一定程度上能相对完美地进行火灾模拟。

通过对国内外相关火灾热释放速率及有关列车的实体火灾试验统计数据调研［6-13］以及Helbing等［14-16］研究结果分析，设定发生火灾时的最大热释放速率为15 MW［17］。

计算中做以下假定［3］：

（1）隧道火灾前，隧道内风流和温度处于相对均匀的状态；

（2）机械通风引起的风流以及燃烧产生的烟气均视为理想气体；

（3）烟气产生后不产生二次化学反应；

（4）隧道衬砌干燥、无渗透；

（5）忽略小型阻碍物、壁面设施和人员运动对风流的影响作用；

（6）忽略燃烧过程中隧道内氧含量对火源的热释放速率以及产烟量的影响。

假定围护结构材料为钢筋混凝土，实体边界定为热厚边界条件，并且假定实体外面温度与设定的环境温度相同，设定为20℃，并保持恒定不变，进入计算区域的新风温度也保持20℃。

利用火灾动力学模拟软件FDS按照全尺寸建立模型（见图3），由于在右线发生火灾时，左线横通道全部处于关闭状态，故在建立模型时只建立了风流流经的部分（正洞、右线横通道、右线2号救援平导、排烟竖井以及排烟斜井）。计算模型从列车发生火灾并停靠在救援站内时开始计算，同时开启风机和横通道门。边界条件根据前文计算结果进行设定。

图3 FDS三维建模模型图

2.2.2 原方案模拟

根据FDS计算结果得出：在作为主进风口的2号救援平导联络通道侧的5#横通道门处风速相当不稳定，而且在模拟计算25 min过程中大部分时间风速达不到2 m/s；同时6#横通道门处风速远远不能达到要求，模拟过程中各处横通道防护门处风速见图4。

图4 各横通道门处风速图

5#和6#横通道中线对应平导内风速分布云图见图5和图6。

利用FDS软件查看平导内风速分布云图，可以看到5#、6#横通道中线对应平导内断面上风速分布相当不均匀，在横通道门侧风速很小，而在远离横通道侧墙壁附近风速可达8 m/s。这种分布造成分风中风流很难进入5#和6#横通道，故需调整原方案。

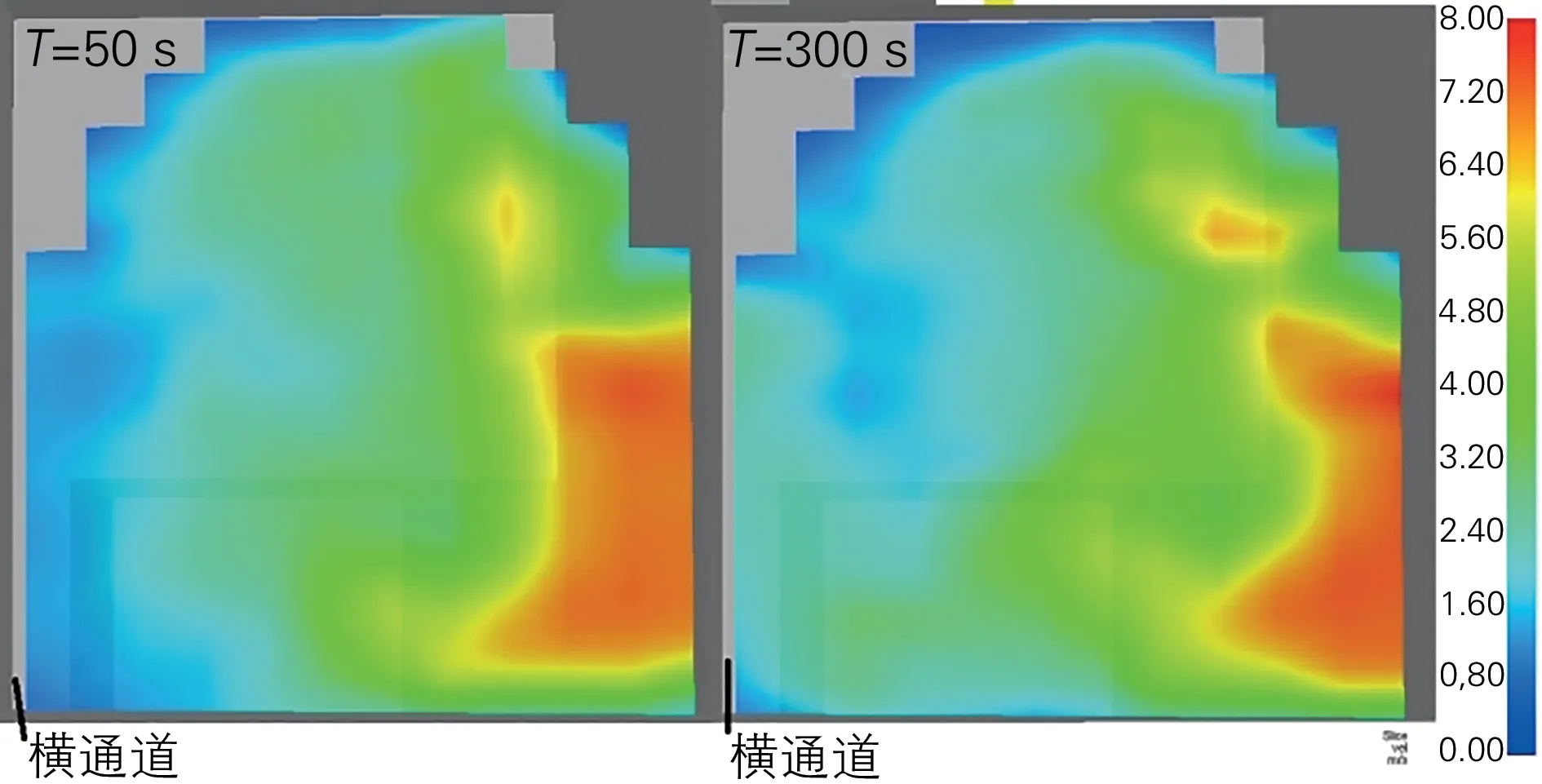
图5 5#横通道中线对应平导内风速分布云图

图6 6#横通道中线对应平导内风速分布云图

2.2.3 调整方案模拟

调整方案首先考虑将横通道间距加大，布置在风速分布相对均匀的地方。规范规定横通道间距最大为60 m，故将5#横通道向隧道进口方向移动5 m，6#横通道向隧道出口方向移动5 m，5#横通道和6#横通道间调整为60 m。计算结果显示5#、6#横通道中线对应平导内断面上风速分布相较移动之前分布差距有所缩小，但仍不均匀，在横通道门侧风速很小，而在远离横通道侧墙壁附近风速可达6 m/s。移动之后5#横通道和6#横通道风速依然达不到要求，甚至影响到7#横通道处风速，使其降低很多。

继续考虑将横通道间距加大，布置在风速分布相对均匀的地方，同时将进风口与平导连接段至5#横通道和6#横通道之间的斜坡部分扩大断面形成喇叭口向平导内送风。修改方案后局部平面图和模型图见图7。

计算结果显示在调整方案修改为喇叭形进风口后，在5#横通道和6#横通道中线对应平导内风速分布相对比较均匀，有利于风流向横通道内（见图8和图9）。

虽然6#横通道门处风速最小，但整个模拟过程中其平均风速约为2.3 m/s，各横通道们风速达到规范要求的2 m/s以上。整个模拟过程中5#横通道门处平均风速约为2.6 m/s，模拟过程中各处横通道防护门处风速见图10。

图7 修改方案后局部平面图和模型图

图8 方案调整后5#横通道中线对应平导内风速分布云图

图9 方案调整后6#横通道中线对应平导内风速分布云图

通过二维和三维计算结果可见：风流具有空间各向异性，在一定情况下不能简单地将其简化为二维空间进行计算。风流具有各向异性，在横断面上分布不一定是均匀的，计算中不能单纯地取其平均值作为断面风速。

3 结论与建议

（1）建议将该隧道救援站的5#和6#横通道间距加大为60 m，并且在联络通道与5#和6#横通道之间加宽断面，以实现喇叭形进风口向平导内送风，使得风流在2号辅助导坑横断面上较均匀分布。

图10 方案调整后各横通道门处风速图

（2）二维通风网络计算仅考虑了线性问题，认为节点上的风速是均匀分布的，未考虑空间性对风速在横断面上分布造成的影响；在隧道通风计算中，特定情况下不能简单将其简化为二维空间进行计算。

（3）建议实际工程中在利用二维通风网络计算出结果后，应通过三维数值模拟进行验证，以便对结构进行优化。