钢铁物流下的卡车排队等待时间预测*

梁 爽 蔡 鹏

（华东师范大学数据科学与工程学院 上海 200062）

1 引言

由于缺乏合理的排队规则，同时因为钢厂业务流程逻辑复杂，原料运输车辆到达钢厂停车场后，很难通过常规手段预估入厂排队等待时间。准确等待时间的缺少使得司机不得不随时呆在车内待命。这种情况既增加了物流成本，也降低了司机的满意度。图1展示了卡车排队卸货的业务流程。

卡车首先进入停车场并按货物品种取得排队号。经过一段时间等待该车被叫号并准备入厂，入厂之后进行卸货工作，卸货完成即可离开厂房。这个过程中，关键的时间信息被实时地记录到钢铁物流信息平台。我们的目标就是预测卡车开始排队至被叫号所花费的时间（既车辆等待时间）。目前大多数钢厂采用排队号乘以固定时间这种依靠经验、粗粒度的预测方法。这种方法忽视了厂内卸货能力、停车场内车辆已等待时间等因素，预测结果对司机参考意义不大。

图1 卡车排队卸货过程

钢铁物流场景下的等待时间预测与一般场景有一定区别。机场出租车等待时间预测［1］考虑机场乘客到达率、天气情况、机场内出租车数量等，银行排队等待时间预测［2］考虑排队号，服务窗口数、业务类型等。这些场景稳定且逻辑相对简单。然而钢铁物流场景下几十种原料运输车辆并行工作，车辆的等待时间受整个工厂状况影响，并且厂内工人数、机器数等变化大，厂区的工作效率也因这些因素动态变化，很不稳定。

时间预测作为一个挑战性的问题，已经在很多应用领域被广泛地研究［3］。常用的高效时间预测模型主要有以下几种：时空模型［4～5］、线性回归模型［6］，神经网络模型［7～9］、支持向量机模型［10～12］、卡尔曼 滤 波 模 型［11～12］、最 近 邻 回 归 模 型（K-Nearest Neighbors，KNN）［1，13］等。然而，由于缺少必要的数据，很少有钢铁物流领域等待时间预测相关的研究。

但随着钢铁物流信息平台的建设，平台产生且不断增加的数据给我们提供了开展研究的契机。我们融合了厂内外排队信息、厂房卸货信息等多个来源的数据建立了初始数据集。我们需要应对两个挑战：1）如何从众多信息中生成有价值的特征；2）如何构建适合钢铁物流这样复杂场景的模型。

由于钢铁物流的复杂性，卡尔曼滤波模型很难构建出其状态方程及观测方程，同时因为钢厂效率的不稳定，时空模型也不适合钢铁物流场景。本文提出一种基于长短期记忆网络［14］（Long Short-Term Memory，LSTM）与线性网络（Linear Network）的组合模型，利用LSTM模型从历史数据中充分获取先验知识，再将先验知识与当前车辆的实时信息结合后利用Linear模型进行较为准确的等待时间预测。在日照钢铁集团真实生产环境下，我们使用Auto-sklearn［15］训练模型来模拟线性回归、支持向量机等方法，并与LSTM-Linear模型对比。

2 钢铁物流数据分析

我们融合了来自京创智汇钢铁物流信息平台的三组真实数据用于卡车等待时间预测，包括厂外卡车排队信息、厂内卡车信息、厂房卸货能力日志。

2.1 排队数据

融合的数据集包括每一辆卡车所运输货物的品种、排队开始时间、叫号时间、入厂时间、出厂时间，车辆所属公司、货物重量、司机信息以及此刻厂房内仓库的卸货能力等。通过融合的数据集中的时间信息，能够清晰地掌握每辆车所处的状态以及各个状态下的车辆流量。

如图2所示，我们统计了2019年7月至2019年10月这四个月来近八万辆卡车的信息，近40种原料主要分为废钢、煤炭、焦炭3个品类。可以看到各个品种之间的特性差异明显，四个月来有些品种只有几十辆车，而有的多达近16000辆；从等待时间来说，有的排队开始即被叫号，而有的等待近10小时。相对来说，3个品类下的品种之间特性更近似。因此下文的实验部分在这3个品类上进行区分。

图2 四个月来各原料品种平均等待时间及车辆数

2.2 特征生成

我们在融合的数据集中找到影响原料运输车辆等待时间的重要因素。表1展示了对一卡车最终生成的7维特征。

表1 由数据分析生成的特征

我们选择一个月破碎废钢的数据为例进行分析。对排队等待时间影响最大是车辆在队列中的排队号。原料运输车辆绝大部分遵循先到先入厂的原则，显然排队号大的车辆应当等待时间更长。如图3（a），大体上排队号与等待时间呈正相关关系。但从图3（b）中，我们发现就算排队号都为15，车辆的等待时间依旧差异很大，这也说明了还存在一些因素影响等待时间。同时将车辆按照等待时间从小到大排序，当前车辆排队号之前的车辆已等待时间越长，当前车辆可能等待时间越短。从图3（c）和图3（d）可看出车辆等待时间与正处于叫号未入厂阶段内的车辆数及这些车辆已等待时间之间呈正相关关系。显然，车辆数越多，等待时间理应更长；同时从实际业务中了解到，车辆被叫号之后即应入厂，如果没有及时入厂，说明厂内状况并不适合车辆入厂，所以出现了图3（d）中的情况，平均已等待时间越长，当前车辆的等待时间可能越长。

图3（e）展示了厂内车辆数与等待时间的关系。绝大部分破碎废钢车辆排队开始时厂内同品种车辆数在5～45之间，一定程度看出等待时间相对稳定（在厂车辆数在50以上的情况很少）。同时我们对工厂压块进行分析，如图3（f），车辆数与等待时间却呈正相关，这种情况也间接说明了钢铁物流的复杂性，不同品种之间既有车辆到达率、等待时间的差异，厂内的工作模式上也存在一定区别。图3（h）展示了距当前车辆排队开始时间最近的10辆同品种已出厂车辆平均在厂时间与当前车辆等待时间的关系。钢厂在一定时间范围内效率是相对稳定的，最近已出厂车辆的在厂时间能够很好反映最近一段时间内厂内的卸货效率。结合图3（g）、3（h），在日照钢厂的实际工作环境下，我们可以根据最近出厂车辆在厂区所花费时间近似了解到厂区的工作效率，推断在厂内的车辆还需多久完成卸货工作，并以此预估仍在厂外等待的车辆需要多久可以入厂。

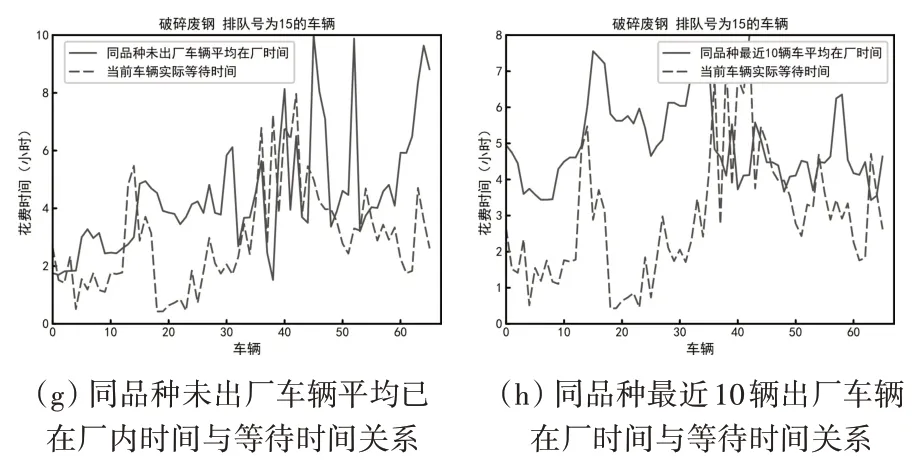
图3 各个特征与等待时间关系

综合以上分析，可以看出钢铁物流场景下的等待时间预测相对于一般场景更为复杂。首先由于缺少必要的数据，很难对钢厂完整状况定量地表示，其次等待时间受到的影响因素较多，各个特征与等待时间之间也并不完全是线性的关系。我们在实际工作过程中通过反复地分析数据，表1所示的7个特征明显影响等待时间。同时，也在这精心选择的7个特征基础上，我们开展了下文模型构建的工作。

3 等待时间预测模型构建

本文提出的钢铁物流场景下的卡车等待时间预测模型由两部分构成：第一部分针对数据量较多（车辆数较多）的品种构建LSTM-linear组合模型，利用LSTM模型，从历史数据中获得对现阶段预测有帮助的先验知识，再利用线性模型，根据当前车辆的实时信息结合先验知识来预测等待时间；第二部分针对数据量很少不足以建模的品种采用KNN回归进行预测。

下面从平台现用方法的弊端、本文提出的等待时间预测模型两方面进行详细说明。

3.1 信息平台现用方法弊端

目前京创智汇钢铁物流信息平台利用线性回归（岭回归）模型实现等待时间预测功能。模型的输入为101维，包括采用独热编码的品种类别、排队号、离当前车辆排队开始时间最近的同品种未叫号20辆车的已等待时间（不足补0）等。这种方法存在明显弊端：1）岭回归模型本身是一个线性回归模型，高达百维的输入可能会降低输入之中有效特征的重要性；2）所有品种糅合在一起，只用一个模型进行预测。假设在很短的一段时间内接连来了两辆运输废钢的车辆，依据岭回归模型的输入对两辆车生成特征，它们的特征向量在排队号的数值相差1，其余特征值区别很小。向量标准化后利用岭回归模型进行预测（y为预测结果，f为标准化后向量，w，b分别为线性模型权重和偏置）：

同时假设在很短的一段时间内接连来了两辆运输煤炭的车辆，抽取特征，两个向量也只在排队号的数值相差1，其余特征值区别很小，利用模型进行预测：

计算这两个品种车辆等待时间的差值（σ为标准化操作中排队号列的标准差）：

然而从图2我们看出废钢、煤炭之间的等待时间差异是明显的，只使用单一的岭回归模型在面对上述情形时显然出现错误，不同品种车辆之间的等待时间差值不应是近似的。

3.2 模型构建

构建单一模型存在一定弊端，所以我们考虑对各个品种单独建模。然而，从图2中看出有不少品种四个月来车辆数较少，数据量很难达到训练模型的要求。所以，对于数据量小于1000的品种我们采取KNN回归的方法利用同品种车辆历史等待时间来预测车辆的等待时间（KNN回归计算基于表1所示的特征）。数据量较多的品种通过建立LSTM-Linear模型进行预测。图4展示了运输车辆的等待时间预测过程。

图4 车辆等待时间预测过程

LSTM是一种能够处理序列变化数据的神经网络。内部门结构的设计使其具备控制信息传递的能力。上一次计算得来的输出传递给下一次的计算，携带了上一次的“记忆”之后，本次计算会在上一次计算的基础上更好的预测，适合排队这样具有时序特点的场景。

在平台现用方法中，忽略了一个重要信息：离当前车辆排队开始时间最近的那些同品种已被叫号车辆的等待时间。这些最新的准确的等待时间对于当前车辆的预测是已知的，同时能很好反映最近厂房内外的状况，利用这些时间能够更好地预测当前车辆的等待时间。我们使用LSTM模型处理这些时序数据，输入最近被叫号车辆的信息，输出对当前车辆的预测。但是，已有准确等待时间的车辆与当前车辆之间存在一段距离，排队号即为距离的长度。如果单纯地用LSTM进行预测，排队中车辆的预测结果势必会近似。所以我们将已叫号车辆的信息与当前车辆实时信息相关联，使用LSTM模型从已叫号车辆的信息中获得对现阶段预测有帮助的先验知识，再利用Linear模型根据实时的厂内外信息输出对当前车辆的预测结果。

图5 LSTM-Linear组合模型示意图

经过多次调试，图5展示了最终LSTM-Linear模型的结构。首先我们将距离当前车辆排队开始时间最近的5辆同品种已被叫号的车分别进行特征工程，生成表1所示的7维向量。最重要的是将这些车的真实等待时间与其特征向量拼接，形成8维的向量，之后将这5个8维向量按排队开始时间顺序拼接作为LSTM模型的输入。设置LSTM模型时间步长为5（与输入五辆车的时间序列保持一致），神经元个数为10的单层网络。之后将LSTM最后一个时间步的输出与3个神经元全连接，我们希望这3个神经元能够从历史数据中带来先验知识，最终的效果也佐证了这个观点。接下来，生成当前车辆的7维特征向量，并将先验知识与当前车辆的特征拼接成10维向量，全连接至1个神经元输出作为预测结果。使用LSTM-Linear模型，我们将历史数据中的信息与实时信息紧密结合，有效提升了预测精度。

4 实验

4.1 评价指标

为了确定预测结果的精度，我们利用三个指标来对预测结果进行评估：误差在半小时以内占比（Error Of Half An Hour，EOHH）、误差在一小时以内占比（Error Of An Hour，EOH）、误差在两小时以内占比（Error Of Two Hours，EOTH）。以EOHH为例，公式如下（I为指示函数，N为总样本数），EOH、EOTH类似。

4.2 实验数据、方法及结果

利用滑动窗口的方式，实验训练集选用钢铁物流信息平台2019年7月25至2019年8月24日近18000条数据，测试集选用2019年8月25至2019年8月30日的3104条数据。为了证明本文所提出的等待时间预测模型的有效性，与平台现用方法（ridge回归），KNN回归［1］，以及利用Auto-sklearn［15］训练出的模型进行比较。Auto-sklearn作为现在流行的自动化机器学习方法，能够自动的进行模型筛选、超参数调节等工作。其中回归模块包含梯度提升决策树、随机森林、支持向量机、高斯过程等多种高效的回归模型。利用Auto-sklearn，我们近似地将一般用于等待时间预测方法应用到钢铁物流场景下。因为废钢、煤炭、焦炭三个品类特性区别明显，因此实验结果依据三个评价指标在三个品类上进行区分。

图6中结果表明本文方法的预测精度在各个品类、各个评价指标上明显优于平台现用方法和KNN回归，只在少部分指标上略低于Auto-sklearn的方法。四种方法在煤炭的预测上精度都较高，因为煤炭的等待时间大多在两个小时以下，同时煤炭等待时间的数值较稳定，所以相对比较容易预测，参考意义最大的EOHH指标本文方法相比平台现用方法有12.8%的提升。废钢的平均等待时间为5个多小时，由于数值波动较大，各个方法EOHH指标较低，因为半小时的误差只占5小时平均等待时间的10%，对于模型预测难度较大。但本文方法在三个指标上相比现用方法分别有33.3%、51.6%、61.2%提升；相比于KNN回归有50%、62.1%、64.6%的提升；相比于Auto-sklearn预测精度分别有9%、11.9%、9.7%的优势。焦炭平均等待时间大概4个小时，但数值波动很大，各个方法预测精度差距不大，但相比于平台现用方法，本文方法在三项指标上依旧有18.5%、21.7%、13.5%的提升。

通过分析，平台现用方法由于仅使用单一线性模型导致预测精度较低。Auto-sklearn训练过拟合严重，钢厂本身也缺少严格的规则，过拟合导致模型泛化能力变弱。规则的缺少也导致KNN回归效果较差。本文方法针对不同品种定制化模型，同时LSTM-Linear模型将历史数据中先验知识与实时信息相结合，利用线性模型输出，减少过拟合，预测精度更高。

4.3 特征重要性

为了评估表1中的特征对等待时间预测的重要程度，我们在破碎废钢上进行了实验。训练集为2019年7月25至2019年8月24日的1924条数据，测试集为2019年8月25日至2019年8月30日的225条数据，测试集的统计量见表2。

图6 各个品类评价指标结果

表2 破碎废钢测试集数据量及统计量

从破碎废钢的统计量看出，等待时间的分布离散程度高，标准差大，侧面反映了预测的难度。我们把LSTM模型的输出称为先验知识，将表1中的特征及先验知识依次加入Linear模型，并对测试集进行三个指标的评估。

很明显排队号对等待时间起到了很大的影响，排队号大小很大程度上决定了等待时间长短。可以认为排队号确定了卡车等待的基准时间，其余表示厂房工作状况的特征影响基准时间的浮动。如果厂房内效率高，等待时间在基准时间的基础上也会有所减小。同时，在加入先验知识之后，模型预测的精度明显提升，说明LSTM模型确实能够从历史数据中带来先验知识帮助现阶段的预测。

表3 特征重要性

5 结语

钢铁物流复杂的业务逻辑使得准确预测卡车排队等待时间变得困难，也因为钢铁物流的特殊性使得卡车等待时间预测区别于一般场景下的等待时间预测。本文详细描述了钢铁物流原料运输车辆的业务流程和数据分析过程，并提出了一种基于LSTM-Linear组合时间预测模型。利用LSTM模型从历史数据中获得先验知识，再结合卡车实时信息通过Linear模型进行高精度的预测。在日照钢铁集团真实的场景下，本文方法的预测精度相比平台现用方法、KNN回归、Auto-sklearn自动构建的模型优势明显。更加精准的等待时间提升了司机的满意度，也有效减少了物流成本。

在以后的研究中，随着物流信息平台进一步完善，我们可以获得更多有用的信息，同时通过合理地选择历史数据训练模型，从而进一步提高预测精度。