小学高段学生数感水平测试问卷编制研究

赵雨晴 吴敏霞 巩子坤

【摘   要】数感是重要的数学核心概念，是小学数学教学中应重点关注的内容之一。基于相关成果、专家意见和学生特点，编制了评估小学4～6年级学生数感水平的问卷。通过两次大规模样本测试，采用探索性因素分析、验证性因素分析等方法，对问卷题目进行修订。最终形成的问卷包含数的意义、数的大小、数与运算、数与估计四个维度。该问卷的信效度良好，可以作为评估小学4～6年级学生数感水平的有效工具。

【关键词】4～6年级学生;数感;问卷编制

一、引言

Tobias Dantzig 在1954年首次提出“数感”（Number sense）这一概念，他认为数感是对微小数量变化的一种直觉感受[1]。2001年，我国在《全日制义务教育数学课程標准（实验稿）》中首次明确提出要培养儿童的数感，随后在《义务教育数学课程标准（2011年版）》中将数感列为十大核心概念之一。由此，数感的内涵、发展规律和培养方法等逐渐成为研究的热点[2-3]。全面考察小学生数感水平的发展特点及其影响因素，可以为小学生数感的培养提供指导。

近年来，针对如何培养学生数感而开展的研究数不胜数，许多数学教育学者都尝试建立有效的测评方法以了解儿童的数感发展，并将其作为一个重要研究方向[4]。Clements[5]、Griffin等人[6]、Malofeeva等人[7]基于儿童数感发展理论设计量表，测评学前以及特定年龄儿童的数感发展状况。张树东等[8]研究4～6岁儿童的数感特点，张丽锦等[9]对一年级儿童的数感展开研究。

本研究基于已有文献，对数感内涵进行再认识，确定其维度并给出操作性定义;编制问卷对学生进行测试，征求专家意见后修改问卷，再次进行大规模样本测试，通过对收集到的数据进行分析，最终形成一套“小学4～6年级数感水平调查问卷”。

二、问卷编制过程与方法

（一）问卷维度及其操作性定义

Sowder[10]认为，有数感的人应当能较好地连接数与运算的概念;能利用数的相对与绝对大小比较数的大小;能以估算的形式判断结果的合理性;掌握心算的方法。马云鹏、史炳星[11]认为，在中小学数学教学中，数感主要是指学生具有应用数字表示具体数据和数量关系的能力;具有选择适当的方法进行计算的经验;能依据数据进行推论，并对数据和推论的精确性和可靠性进行检验。数学教育工作者Der-Ching Yang对数感的组成成分进行了如下分类：理解数的意义;辨别数的相对大小;恰当地运用基准量;理解运算对数的影响;恰当运用不同的解题策略得出结果，并能判断结果的合理性。

由此可见，目前数学教育领域普遍认为“数感”是对数的概念、数与运算、数字关系和数字模式的理解，以及运用数学知识解决问题的能力。结合以往研究和课标要求，进行文献梳理后，与数学教育专家及小学优秀教研员多次探讨小学阶段数感的内涵，归纳出以下四个重要维度：数的意义、数的大小、数与运算、数与估计。由此，建构了数感的维度以及各个维度的含义和操作性定义（如表1）。

（二）问卷题目的建立

根据问卷题目编制的注意事项[12-14]，分析每份问卷的题项。考虑到小学4～6年级学生相比低段学生，在思维方式方面出现了较大变化，形象思维开始向抽象思维和逻辑思维过渡[15]，并且已经学习了用字母表示数，因此改编现有问卷题目时，以字母代替图形符号，形成了含有44道题目的初始问卷（记为问卷一，见表2）。题型均为选择题和填空题，每空记为1题（如第1题，该填空题有2空，记为2题），另外数与运算和运算结果估计的题目还需学生填写选择的理由。

（三）被试选取与问卷回收

整个问卷的编制过程一共进行了三次测试，测试后的分析以及问卷修订详见下文“预调查问卷的分析与修订”。第一次发放问卷（问卷一）的对象为杭州市G区某小学五年级学生4人，测试后对学生进行访谈，了解学生对题目的理解情况。

第二次发放问卷（问卷二）用于问卷修订过程中的探索性因素分析。选取杭州市X区某小学的四、五、六年级学生作为样本，总样本量为385人，回收有效问卷377份，有效率为97.9%。

第三次发放问卷（问卷三，见附录）用于问卷修订过程中的验证性因素分析。选取杭州市G区某小学的四、五、六年级学生作为样本，总样本量为442人，回收有效问卷434份，有效率为98.2%。

（四）数据分析

问卷中每题正确记1分，错误记0分。另外数与运算以及运算结果估计的题目需要填写选择的理由，答案正确但理由不合理记为1分，答案正确且理由合理记为2分，其余情况记为0分。利用 SPSS 22.0对数据进行项目分析、相关分析、探索性因素分析，利用 AMOS 24.0 对数据进行验证性因素分析。

三、预调查问卷的分析与修订

（一）问卷试测

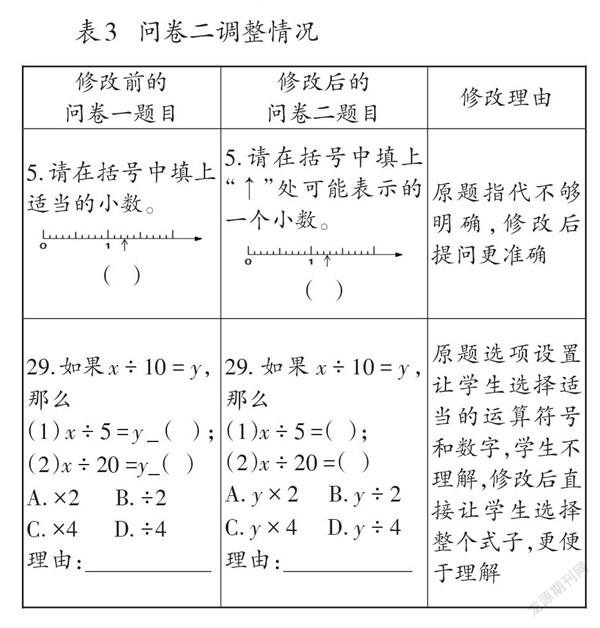
第一次测试（问卷一）的目的是避免学生因生字生词而读不懂题目，导致无法作答或作答错误。测试后通过访谈了解学生对题目的理解情况，在不改变题意的情况下，为便于学生理解，修改了其中3题的提问方式（详见表3），并将问卷中出现的所有图按顺序进行编号，形成问卷二。

（二）项目分析

第二次测试（问卷二）后，回收问卷，录入数据。

采用相关系数法，考察问卷中每道题与总分的相关性，最终发现，每道题目与总分均相关。采用临界比率法（CR）对被测学生的得分进行差异性检验[16]，即计算每份问卷总分后，按总分从高到低排序，前27%（102人）为高分组，后27%（102人）为低分组，对两组进行独立样本t检验，删除不具有高低分组显著性差异的2道题目（第3、12题）。

3.在五位数35698中，减去5个千后，得到的数是_____。

12.下图中，涂颜色的圆占了全部圆的（     ）。

A.[46]      B.[610]       C.[410]      D.[64]

（三）探索性因素分析

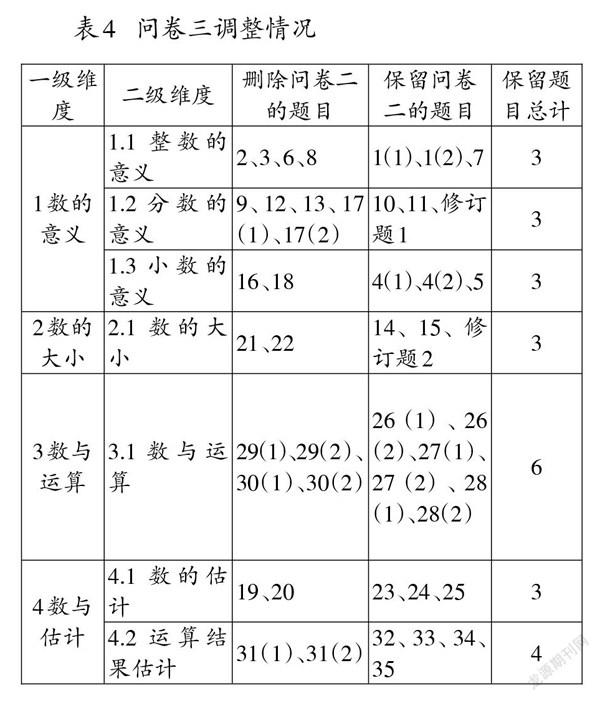
基于项目分析，对数据进行探索性因素分析。首先对问卷结构进行检验，发现问卷的KMO值为0.868，Bartlett球形度检验显著（p=0.000<0.05），表明适合做因子分析。选择主成分分析法和最大方差旋转法进行分析，检验问卷维度以及相应题目。筛选问卷中的题目时主要遵循如下原则[17]：（1）保留因子特征值大于1的题目;（2）保留因子载荷值至少在0.4以上的题目;（3）删除在两个以及两个以上的因子载荷值均大于0.4的题目。最后共计删除21道题目（详见表4），保留23道题目。

在探索性因素分析后，问卷的7个二级维度作为主成分被保留，但是其中“1.2分数的意义”和“2.1数的大小”只剩2题，按照问卷编制要求，每个子维度下至少包含3题，因此在这两个维度下各修订1题（见附录第6题，第9题），形成问卷三，共25题（详见表4与附录）。

四、问卷的检验

（一）验证性因素分析

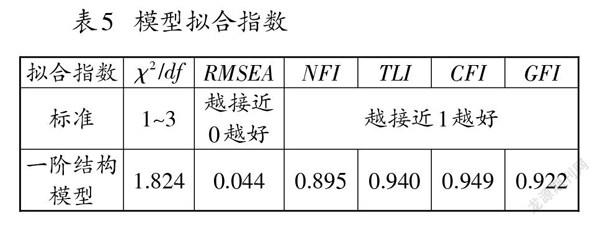
第三次测试（问卷三）后，回收问卷，录入数据，对数据进行验证性因素分析，检验实际数据模型与理论模型的拟合程度，如表5所示[18]。

第一步，进行一阶两两相关模型验证因素分析。根据分析结果，通过残差进行修正，综合考虑各项指标，一阶因子的模型拟合程度较好，一阶因子概念之间存在高度相关性，可进行下一步[19]。

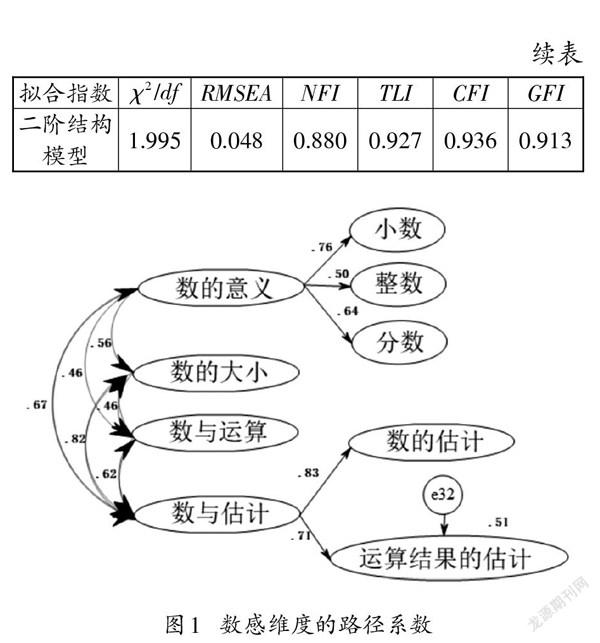
第二步，进行二阶两两相关模型验证因素分析。评价指标同第一步，综合考虑各项指标，模型拟合程度较好。最终的维度路径系数见图1。

（二）问卷的信度和效度分析

1.信度分析

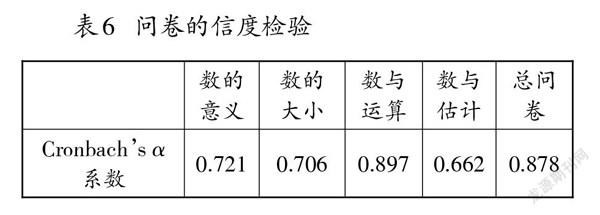
为了评估问卷的一致性、可靠性和有效性，采用Cronbach’s [α]系数计算问卷的内部一致性，对问卷进行信度检验。分别计算数的意义、数的大小、数与运算、数与估计4个维度以及总问卷的内部一致性信度（[α]系数），各项指标均达到标准（见表6），表明问卷的信度良好。

2.效度分析

（1）内容效度：检验问卷实际测试的内容与所要测试内容之间的吻合程度[20]。目前，应用最广泛的指标是内容效度指数（CVI）[21]。在问卷形成后，邀请4位专家（2位高校教师，2位教研员）对问卷题目与相应维度的关联性进行打分。采用4等级评分：1=不相关，2=弱相关，3=较强相关，4=非常相关。打分完成后计算Kappa值（K*，0.60～0.74 为良好，大于 0.74 为优秀），结果如表7所示。

进一步计算问卷的内容效度值（S-CVI），结果显示S-CVI/UA（被所有专家均评为3分或4分的题项数量占全部题项数量的百分比）为 0.80，S-CVI/Ave（问卷所有条目I-CVI的平均数）为 0.95。根据S-CVI/UA不低于 0.80，S-CVI/Ave应达到0.90的标准，本问卷的内容效度达到标准。

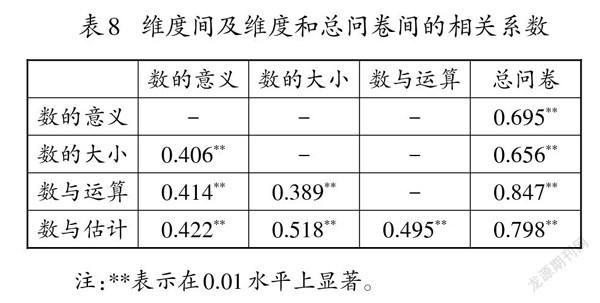
（2）结构效度：以验证性因素分析的结果和问卷各维度间、各维度与总问卷间的相关系数作为检验指标[22]。在二阶模型拟合指数中，[RMSEA]的值小于0.05，[TLI]与[CFI]的值大于0.9，这时拟合的模型是一个“好模型”[23]，结构效度达到要求。问卷各维度间、各维度与总问卷间的相关系数如表8所示，各维度之间存在着显著的中度相关，相关系数在 0.389～0.518之间，各维度与总问卷之间存在中高度显著相关，相关系数在0.656～0.847之间。分析表明，问卷所确立的4个一级维度之间有相对独立性，各个维度与问卷整体相关性较大，因而问卷的结构效度较好。

五、讨论

本次编制的“小学4～6年级数感水平调查问卷”在维度上沿用了研究者先前编制的“小学1年级数感水平调查问卷”[24]和“小学2-3年级数感水平调查问卷”[25]，但相比之下，本次问卷编制过程更严谨，具有科学性，主要体现在以下方面。

（一）大样本选取

本次问卷编制过程中进行探索性、验证性因素分析时选取的样本量均在400人左右，流程为：基于对大样本数据的探索性因素分析，对问卷进行修订;再进行大样本测试，对问卷进行验证性因素分析。

（二）问卷编制过程具有严谨性、科学性

本次问卷编制过程共进行三次测试。初始问卷包含44道题目，先经过试测，修改了2道题的提问方式，保证学生在测试过程中不会因为不理解题意而发生错误。第二次大规模测试后对结果进行项目分析和探索性因素分析，修订题目，形成结构合理的最终版本测试问卷，共包含25道题目。为了检验最终问卷的信度和效度，进行第三次大规模测试，对数据结果进行验证性因素分析和信效度检验。本次问卷编制过程参照王光明等[26]编制问卷的方法，具有严谨性、科学性。

（三）问卷题目设计合理，结构完整，一脉相承

针对小学生数感的发展与特征，郭民[27]依据数感阶段的划分以及数感的构成要素设计了一套问卷用于测试2～6年级的所有学生，而本研究依据小学1～6年级学生的不同水平，设计了三套问卷。“小学1年级数感水平调查问卷”包括数字运算、数字意义、数字表示、数字关系、数字估计、问题情境六个维度，而“小学2～3年级数感水平调查问卷”在维度上有所调整。经过探索性因素分析，确定问卷结构包括数的意义、数的大小、数与运算、数与估计四个维度，因此“小学4～6年级数感水平調查问卷”沿用了这四个维度，使系列问卷一脉相承，具有系统性。本问卷含25道题目，数量合理，学生能在一课时内完成。

六、结论

“小学4～6年级数感水平调查问卷”的编制过程具有严谨性、科学性，问卷具有良好的信效度，可作为评估4～6年级小学生数感水平的有效工具。

参考文献：

[1] DANTZIG T.Number： The language of science[M].New York： Macmillan，1954：4-5.

[2] 郑婷.数感的内涵、价值与培养策略[J].小学数学教育，2019（10）：20-22.

[3] 周卫. 小学阶段数感培养的策略研究[D].上海：上海师范大学，2012.

[4]赵振国.3～6岁儿童数感发展的研究[J].心理发展与教育，2008（4）：8-12.

[5]CLEMENTS D H. Training effects on the development and generalization of Piagetian logical operations and knowledge of number[J]. Journal of Educational Psychology， 1984， 76（5）：766-776.

[6]GRIFFIN S A， CASE R， SIEGLER R S. Rightstart： Providing the central conceptual prerequisites for first formal learning of arithmetic to students at risk for school failure[J]. Classroom lesson：Integrating cognitive theory and classroom practice， 1994：25-49.

[7]MALOFEEVA E ， DAY J ， SACO X ， et al. Construction and Evaluation of a Number Sense Test With Head Start Children[J]. Journal of Educational Psychology， 2004， 96（4）：648-659.

[8]张树东，夏学楠，张文秀.4～6岁儿童数感发展研究[J].中国特殊教育，2018（12）：82-89.

[9]张丽锦，毕远，梁熠，等.小学一年级数感不良儿童的筛查与动态干预[J].心理学报，2016，48（7）：804-817.

[10]SOWDER J T. Estimation and number sense[J]. Handbook of research on mathematics teaching and learning： A project of the National Council of Teachers of Mathematics， 1992：371-389.

[11] 马云鹏，史炳星. 认识数感与发展数感[J]. 数学教育学报，2004，11（2）：46-49.

[12] 赵必华，顾海根.心理量表编制中的若干问题及题解[J].心理科学，2010，33（6）：1467-1469.

[13] 郑日昌.心理测量与测验[M].北京：中国人民大学出版社，2008：107-120.

[14] KLINE P. A handbook of test construction：introduction to psychometric design [M]. New York： Routledg， 2015： 116-121.

[15] 趙志明.探究小学高段数学如何开展创新教学[J].课程教育研究，2020（12）：136-137.

[16] 王光明，廖晶，黄倩，等.高中生数学学习策略调查问卷的编制[J].数学教育学报，2015，24（5）：25-36.

[17] 王光明，刘丹.初中生数学学习策略调查问卷的设计与编制[J].数学教育学报，2017，26（3）：19-24.

[18] 余晓娟，林子植，徐章韬.结构方程模型在数学教育研究中的应用[J].教育测量与评价，2019（4）：18-24.

[19] 王光明，佘文娟，王兆云.高中生数学元认知水平调查问卷的设计与编制[J].心理与行为研究，2016，14（2）：152-161.

[20] 史静琤，莫显昆，孙振球.量表编制中内容效度指数的应用[J].中南大学学报（医学版），2012，37（2）：49-52.

[21] Hambleton R K ， Swaminathan H ， Algina J ， et al. Criterion-Referenced Testing and Measurement： A Review of Technical Issues and Developments[J]. Review of Educational Research， 1978， 48（1）：1-47.

[22] 侯杰泰，温忠麟，成子娟.结构方程模型及其应用[M].北京：教育科学出版社，2004：45.

[23] 崔宝蕊，李健，王光明.初中生数学元认知水平调查问卷的设计与编制[J].数学教育学报，2018，27（3）：45-51.

[24] 俞飞丹. 基于脑电的一年级学生数感研究[D].杭州：杭州师范大学，2017.

[25] 滕林林. 基于ERP的低段学生数感发展研究[D].杭州：杭州师范大学，2018.

[26] 王光明，宋金锦，王兆云. 高中生数学学习非智力特征调查问卷的编制[J]. 数学教育学报，2015（3）：17-27.

[27] 郭民. 小学生数感的发展与特征研究[D].长春：东北师范大学，2009.

附录：问卷三

亲爱的小朋友：欢迎参加小测试。请你仔细看题目，按照要求认真回答。选择题都只有一个正确答案。测试结果只用来做研究，与你的数学成绩无关。

1.请在括号中填上“↑”处可能表示的一个小数。

<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼1_1.jpg>（     ）

2. 1.57里面有15个（    ），7个（    ）。

3. 4367是由43个（    ）和67个（    ）组成的。

4.小华在用计算器计算369070+430102时，因为按错了键，计算结果多出了30000，他出错的原因可能是（     ）。

A.将369070中的6按成了3

B.将430102中的3按成了6

C.将369070中的3按成了6

D.将430102中的3按成了9

5.下面（     ）图形中的阴影部分的面积占总面积的[13]。

A.<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼2.jpg>    B.<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼3.jpg>  C.<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼4.jpg>

6.在下图中涂颜色的圆占全部圆的[15]的是（   ）。

A.①和②        B.①和③

C.②和③        D.①②和③

<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼5.jpg><Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼6.jpg><Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼7.jpg>

图①                    图②                     图③

7.在下图中涂颜色的圆占全部圆的[14]的是（   ）。

A.④和⑤        B.④和⑥

C.⑤和⑥        D.④⑤和⑥

<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼8.jpg><Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼9.jpg><Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼10.jpg>

图④                  图⑤                   图⑥

8.把[57]，58%，0.57，[35] 四个数，从小到大排列是（   ）。

A.[35]，0.57，58%，[57]                         B.[35]，0.57，[57]， 58%

C.0.57，[35]，[57]，58%        D.0.57，58%，[35]，[57]

9.把[89]，48%，0.49，[25] 四個数，从小到大排列是（   ）。

A.[89]，0.49，48%，[25]        B.0.49，[25]，48%，[89]

C.[25]，48% ，0.49，[89]       D.[25]，0.49，[89]，48%

10.把[113]，131%，1.3三个数，从小到大排列是（    ）。

A.1.3，131%，[113]            B.131%，1.3，[113]

C.1.3，[113]，131%            D.131%，[113]，1.3

11.小李和小华带了一样多的钱出门，小李花了[13]，小华花了30%。请问，谁剩下的钱多（   ）。

A.小李              B.小华

C.一样多           D.无法比较

12.小明今天走了10179步，他每天坚持走差不多的步数，那么他走1亿步大约需要（   ）。

A.3个月     B.30个月     C.3年     D.30年

13. 如图⑦，有一个正方形的花园，绕它的周围走一圈。假设你从O点出发，顺着箭头方向走，大约走了整个路程的[13]后，你的位置大约在哪里（   ）。<Z：＼2021年教师类小学版＼2021年小学数学＼小学数学2021-12＼小学数学2021第12期内芯＼Image＼11.jpg>

图⑦          A              B              C       ;      D

14.如果[a]+59=321，那么

（1）[a]+20+（    ）=321;（2）[a]-20+（    ）=321。

A.39         B.59         C.79         D. 99

理由：

15.如果[b]×10=[c]，那么

（1）[b]×（   ）=[c]×3;（2）[b]×（   ）=[c]÷2。

A.5              B.10              C.20               D. 30

理由：

16.如果[m]-[n]=60，那么

（1）（[m]+20）-[n]=（   ）;（2）[m]-（[n]+20）=（   ）。

A. 20              B. 40             C. 60              D.80

理由：

17.有甲、乙、丙三個数，甲=99×399，乙=398×99，丙=399×101，下列对甲、乙、丙三个数的大小顺序的叙述，哪一个是正确的（   ）。

A.甲=乙=丙      B.甲>乙>丙

C.乙>甲>丙      D.丙>甲>乙

理由：

18.[a]，[b]，[c]都是非零自然数，且[b>c]，那么[a-b+c]和[a+b-c]谁更大（   ）。

A.[a-b+c]      B.[a+b-c]

C.一样大      D.无法比较

理由：

19.[x]，[y]，[z]都是非零自然数，且[y>z]，那么[x÷y×z]和[x×y÷z]谁更大（   ）。

A.[x×y÷z]      B.[x÷y×z]

C.一样大      D.无法比较

理由：

20.[m]，[n]，[s]，[t]都是非零自然数，且[m÷1.1=n÷0.9=s÷34=t÷65]，那么最小的数是（   ）。

A.[m]           B.[n]            C.[s]           D.[t]

理由：

（1.浙江省杭州长河中学   310053

2.浙江省杭州市余杭区良渚杭行路小学   311101

3.杭州师范大学经亨颐教育学院   311121）