京沪高铁隧道背景下列车车体动态气密性当量泄漏面积阈值特征
万有财, 李 明, 张 雷, 刘 斌, 梅元贵
(1.兰州交通大学 甘肃省轨道交通力学应用工程实验室,兰州 730070;2.中车唐山机车车辆有限公司,河北 唐山 064099)
高速列车通过隧道诱发车外剧烈压力波动,车外压力波动通过车门、车窗、空调通风口以及地板穿线孔等部件不规则长度各异的缝隙传入车内,引起司乘人员耳感不适问题[1-2]。为保证车内人员压力舒适性,除采取加大了隧道净空面积措施外,在列车方面采取了气密性车体和加装了压力保护装置。用来描述列车气密性的常用物理量是时间常数和当量泄漏面积两个气密参数。目前各国采用静态时间常数来规定高速列车的气密性:日本和法国等规定车内压力由4 000 Pa降至1 000 Pa的时间必须大于50 s;德国和意大利规定车内压力由3 600 Pa降至1 350 Pa的时间必须大于18 s;中国规定[3]车内压力由4 000 Pa降至1 000 Pa的时间必须大于40 s(速度等级在200 km/h~250 km/h)和50 s(速度等级在250 km/h~350 km/h)。时间常数虽能以车内压力泄压时间的长短简洁地表示车体气密性的好坏,但物理意义并不直接明了,对优化列车各部件的气密性、空调通风和压力保护技术系统的比选和设计缺乏一定的定量指导价值。气密性车体会较大幅度的提高列车制造和维护成本,根据压力舒适性要求,确定车体气密性值,对合理设计和运营维护列车有直接的指导意义。
列车通过隧道引起的压力波要比明线交会压力波要剧烈得多,是评价和考核耳感舒适性问题的主要工程场景。国内外学者针对列车通过隧道时车外压力波问题主要利用实车试验、模型试验和数值仿真等技术展开研究[4-5]。尤其是一维流动模型特征线数值模拟方法被得到广泛应用:Vardy[6-7]基于一维可压缩非定常等熵流动模型发展起来的Thermo Tun[8]商业软件;Woods等[9-11]采用一维可压缩非定常不等熵流动模型研究压力波。针对车内压力:Yamamoto[12]根据车内外空气质量交换实际特征和质量守恒定律,提出“当量泄漏面积”表示车体气密性方法,并给出考虑列车通风实际特点的车内压力计算模型;Klingel[13]考虑车体压缩性采用细长孔泄漏模型,提出“时间常数”表示车体气密性方法,并建立了车内压力计算模型;Sima等[14-15]考虑车体压缩性并结合细长孔和薄壁孔两种不同泄漏模型建立了“C1、C2参数法”计算车内压力;张光鹏等[16]建立“热力学模型”计算车内压力;闫亚光等[17]采用三维数值模拟研究了两列车隧道内交会时,列车速度、列车长度、密封性及隧道内不同会车位置对车内压力变化最大值的影响。上述研究工作从不同角度重点研究了车内外压力,但未对列车的气密性阈值展开研究。
Nam[18]未考虑车体压缩性采用时间常数评价了列车气密性;Sima等[19]利用实车试验测得的车内外压力数据采用试凑法得出了动态时间常数和泄漏面积值;余南阳等[20]以京沪线为背景,利用时间常数研究车内压力及舒适性特征;李国清等[21]采用静态试验采用当量泄漏面积对高速综合检测列车车体密封进行了评估;许良中等[22]基于实车试验测得的车内外压力,分析了单车明线工况下车体动态时间常数随时间的变化关系,针对旅客耳感不适问题提出了改进措施;梅元贵采用时间常数针对特长隧道耳感不适问题进行了研究,建议在特长隧道条件下采用多时间间隔压力变化阈值来评价耳感舒适性;史宪明等[23]采用一维特征线法,以时间常数表征动车组气密性能,研究了不满足车内压力舒适性标准的隧道长度区间;张芯茹等[24-25]等基于压力舒适性标准,采用数值模拟方法研究了列车的动态气密时间常数阈值。
从国内外目前研究看,尽管提出了不同速度等级的高速列车车体气密性的要求,但结合舒适性标准、实际隧道压力波特征等,研究车内压力特征,提出动态当量泄漏面积的阈值要求的成果未见到公开报道。京沪客运专线是我国高速铁路发展的代表,目前商业运营速度已达到350 km/h,本文以京沪客运专线为背景,基于一维可压缩不等熵非定常流动模型的广义黎曼变量特征线法数值模拟得到车外压力;未考虑车体压缩性,选用薄壁孔流动模型,建立车内外压力关系—“当量泄漏面积法”,利用改进欧拉法求解微分方程得到车内压力;基于500 Pa/s、800 Pa/3 s和1 000 Pa/10 s三种车内压力舒适性标准,从动车组编组长度、速度和通过方式三方面对中国某型号标准动车组动态气密性展开研究,给出动车组在不同速度等级下单节车厢动态当量泄漏面积阈值的建议值,为动车组气密性设计提供基础性技术参考。
1 研究方法
本文利用数值模拟方法求解车外压力;基于静态试验数据验证了本文所建立的计算车内压力方法的合理性及程序的准确性;在满足压力舒适性标准的条件下,数值求解动态当量泄漏面积阈值。
1.1 物理模型


图1 等效泄漏模型示意图
1.2 车外压力波数值计算方法
动车组通过隧道所引起的三维流动可简化为一维可压缩非定常流动,考虑到隧道内空气与动车组壁和隧道壁之间存在摩擦和传热,流动是不等熵的,所以本文采用一维可压缩非定常不等熵流动模型[26]来求解车外压力。描述流动的控制方程如下
连续性方程
(1)
动量方程
(2)
能量方程
(κ-1)ρ(q-ξ+uG)
(3)
式中:u、p、κ、ρ和a分别为隧道内空气流速、压力、比热比、密度和声速;F为空气流道横截面面积;G为空气与壁面的摩擦项;q为空气与壁面的传热项;ξ为空气与列车壁面的摩擦功;t为时间。式(1)~式(3)构成了一阶拟线性偏微分方程组,利用广义黎曼变量特征线方法求解。
1.3 车内压力求解方法
列车过隧道车厢内外存在压差,通过车厢泄漏孔存在向内充气和向外漏气两种过程,充气或漏气过程的空气为理想气体的绝热等熵流动,忽略车体变形,利用伯努利方程得到空气流速
(4)
空气的质量流量为
(5)
在绝热充气/漏气过程中,车厢内压力变化率和流入/流出的空气质量流量有以下关系
(6)
结合式(4)~(6),再根据声速公式a2=κ·Rg·T得出计算车内压力式(7),计算车内压力时,初始时刻车内压力值取零时刻的车外压力值,文中在已知车厢外压力的条件下,采用改进的欧拉法求解式(7)得到车内压力
(7)
文中采用数值方法求解车外压力时,选取的时间步长很小,由流场的连续性可知,压力不会突变,故可认为在较短时间内车外压力变化较小,基本保持不变,假设车外压力在Δt(Δt=t2-t1)时间内是几乎不变的,积分式(7)后变形可得当量泄漏面积的计算式
(8)
式(4)~(8)中:Δp=pi-pa,pi和pa分别为车厢内外压力值;a、κ、T、ρ和Rg分别表示空气声速、比热比、温度、密度和气体常数;t为时间;V为每节车厢的内部净空体积;Seq为单节车厢总当量泄漏面积;式(7)中负号表示漏气:pi>pa;正号表示充气:pi 根据车外压力值,结合1.3节介绍的方法可计算得到各个时刻的车内压力值,车内外压力均可看作关于时间t的连续函数。图 2给出了统计任一tk时刻车内不同时间间隔内最大压力变化量的流程图。n表示不同的时间间隔,t1和t2时刻对应的车内压力值分别为p1和p2,假使最终确定出最大压力值为p1,最小压力值为p2。若t1>t2,则每n秒内的最大压力变化量Δp=p1-p2,表示该时间段内车内压力最大值出现在最小值之后;若t1 图2 统计车内不同时间间隔内最大压力变化量流程图 图3给出了车厢当量泄漏面积阈值的估算流程图。由图3可知:已知车外压力,先估算一个当量泄漏面积值,根据车外压力利用式(7)求解得到车内压力;根据求解的车内压力,计算车内不同时间间隔内最大压力变化量,对比车内不同时间间隔内最大压力变化量的最大值是否符合对应车内压力舒适性标准允许的最大值,若符合对应的舒适性标准,则所估算的当量泄漏面积值即为对应的当量泄漏面积阈值,若不符合对应的舒适性标准,循环此过程估算当量泄漏面积直至符合压力舒适性标准。 图3 估算车厢当量泄漏面积阈值流程图 本文采用可压缩不等熵非定常流动模型的广义黎曼变量特征线法源代码程序模拟车外压力,图 4给出了单列CRH400BF动车组通过大西线忻州隧道时,头车中部测点的实车试验结果与一维程序结果对比,纵坐标Δp表示车外压力相对于大压力的相对值,表1给出了实车试验基本参数。数值计算得到的车外压力波动趋势与实车试验结果吻合度良好,头车平直车身中部测点最大正负压值与实车试验的误差分别1.49%和4.47%。计算精度可满足工程需求,说明了本文车外压力数值模拟方法的合理性和程序的准确性。 图4 计算车外压力程序验证 表1 实车试验基本参数 本文利用Sima给出的静态泄压试验数据来验证计算车内压力方法的合理性和程序的准确性。结果如图5所示,纵坐标Δp表示静态泄压实验时车厢内压力相对于车厢外压力的相对值,车厢泄漏面积为16.5 cm2。本文计算结果在12.5 s左右达到最大误差3.4%,与文献试验结果相比,吻合度良好,说明本文车外压力数值模拟方法的合理性和程序的准确性。 图5 计算车内压力程序验证 (1) 计算参数 本文以中国某型号标准动车组为研究对象,动车组和隧道的具体参数见表2,本文研究头/尾车的气密性时,将头/尾车的客室和司机室内的净空体积进行了相加。 表2 动车组与隧道基本参数 京沪线上共有22座隧道,总长度16 km,本文选择了隧道长度大于500 m的10座隧道展开研究,表3给出10座隧道的具体名称和对应长度。 表3 京沪线部分隧道 (2) 舒适性标准 本文研究动车组的最低速度为300 km/h,且京沪线上最长的隧道为2 812 m,16编组动车组全程通过时间不到40 s,所以本文选用UIC中规定的多时间间隔下的三个压力舒适性标准:500 Pa/s、800 Pa/3 s和1 000 Pa/10 s。 为了阐明车内外压力波的形成机理,图 6表示两列16编组动车组以350 km/h的速度在西渴马1号隧道中央等速交会时车内外压力及车内每3 s内最大压力变化量时间历程曲线。满足车内最大压力变化幅值≤800 Pa/3 s时头、尾车当量泄漏面积阈值分别为30.0 cm2和32.6 cm2。 图 6(a)表示头尾车通过隧道诱发的压缩波和膨胀波的轨迹线,车头和车尾鼻尖运行轨迹,黑色实线/划线分别表示车头/尾鼻尖运动轨迹。红色(绿色)实线和短划线分别表示压缩波和膨胀波轨迹线。图 6(b)和(c)中垂直于横坐标的红色(绿色)实线和短划线分别表示压缩波和膨胀波,垂直横坐标的黑色实线和黑色划线分别表示两列动车组头头交会和尾尾交会瞬间。“C”表示压缩波,“E”表示膨胀波,“N”表示车头,“T”表示车尾;例如,“C1N”和C2N分别表示第一列动车组和第二列动车组的车头驶入隧道入口端产生的初始压缩波,“E1N”和E2N分别表示该初始压缩波在隧道端口经过一次反射后形成的膨胀波,“C1N1”和“C2N1”分别表示该初始压缩波在隧道端口经过两次反射后形成的压缩波。图 6(b)和(c)中左侧纵坐标Δp表示车外压力相对于大压力的相对值,文中后续出现的车外压力值均是相对于大气压力的相对值。 由图 6(b)和(c)可知;动车组在隧道内交会的车外压力波动,是压缩波和膨胀波共同作用的结果—车身测点遇压缩波压力升高,车身测点遇膨胀波压力下降。动车组在隧道中央等速交会,头车车外压力呈“先正后负”、尾车呈“先负后正再负”的规律。车外压力波动通过车厢的缝隙传入车内引起车内的压力波动,车内压力波动趋势与车外一样,由于动车组有一定的密封性,使得车内压力的波动幅值明显小于车外的。由图 6(b)和(c)可知:头尾车车内每3 s内最大压力变化量均在18 s左右达到规定的阈值,若车厢泄漏面积大于泄漏面积阈值,车内压力便不能满足800 Pa/3 s压力舒适性标准。 动车组以同一速度通过不同隧道,当车内压力符合同一种舒适性标准时,便会产生不同的当量泄漏面积阈值。本文把同一编组动车组以同一速度通过不同长度隧道时,车内压力符合同一种舒适性标准时产生的当量泄漏面积阈值中最小的称为“当量泄漏面积阈值的最小值”。 (a) 列车运行轨迹图和波反射图 (b) 头车 (c) 尾车 图7表示16编组动车组通过以350 km/h速度通过1 905 m隧道时,头车当量泄漏面积分别取25.2 cm2(符合1 000 Pa/10 s标准时的当量泄漏面积阈值)和87.9 cm2(符合500 Pa/s标准时的当量泄漏面积阈值)时,车内每1 s、3 s和10 s内最大压力变化量时间历程曲线。图中平行于横坐标的三条实线表示500 Pa/s、800 Pa/3 s和1 000 Pa/10 s的阈值。由图7可知:当量泄漏面积为25.2 cm2时,车内每1 s、3 s和10 s的最大压力变化量均分别小于其阈值500 Pa、800 Pa和1 000 Pa;当量泄漏面积为87.9 cm2时,车内每1s的最大压力变化量小于其阈值500 Pa,而车内每3 s和10 s的最大压力变化量均分别大于其阈值800 Pa和1 000 Pa。这说明满足车内压力1 000 Pa/10 s标准时的当量泄漏面积阈值也会满足其它两个标准。 五个流态化反应器串联在一起形成环形系统,当首槽料层含镉达85%以上或尾槽后液镉持续超出0.001g/L,首槽退出,其后反应器作首槽,新并入反应器作尾槽。 (a) 当量泄漏面积Seq=25.2 cm2 (b) 当量泄漏面积Seq=87.9 cm2 图8表示16编组动车组以350 km/h的速度通过692 m、1 097 m、1 504 m和1 905 m四个不同长度隧道,头中尾车内压力符合三种不同舒适性标准时的当量泄漏面积阈值变化曲线,由图 8可知:动车组以350 km/h速度通过同一隧道时,车内压力符合不同舒适性标准的当量泄漏面积阈值不同,且当量泄漏面积阈值按符合500 Pa/s、800 Pa/3 s 和1 000 Pa/10 s标准依次减小。 (a) 头车 (b) 中间车 (c) 尾车 表4统计了16编组动车组以350 km/h速度通过京沪线长度大于500 m的10个隧道,车内压力符合三种不同舒适性标准的当量泄漏面积阈值的最小值。由表 4可知:车内压力符合1 000 Pa/10 s标准时,取得当量泄漏面积阈值的最小值,所以本文后续着重以1 000 Pa/10 s的标准展开研究。 表4 不同舒适性标准下当量泄漏面积阈值的最小值 图9表示8编组和16编组动车组分别以380 km/h的速度通过692 m、1 097 m、1 504 m和1 905 m四个不同长度隧道,头中尾车内压力符合1 000 Pa/10 s标准时的当量泄漏面积阈值变化曲线。由图 9可知:8编组动车组通过692 m、1 097 m和1 504 m三个隧道,车内压力符合1 000 Pa/10 s标准时取得的当量泄漏面积阈值比16编组的小。由图 9(a)可知:8编组和16编组动车组以380 km/h的速度通过1 097 m隧道,车内压力满足1 000 Pa/10 s标准时头车当量泄漏面积阈值均小于45.0 cm2,但8编组的比16编组的小。 (a) 头车 (b) 中间车 (c) 尾车 为分析说明8编组动车组车体当量泄漏面积阈值为何小于16编组的,图10表示8编组和16编组单列动车组以380 km/h的速度通过1 097 m隧道时,头车车外压力和头车(当量泄漏面积为均45.0 cm2)内每10 s内最大压力变化量随时间的变化曲线。由图 10可知:16编组动车组的头车外最大压力峰峰值比8编组的大;当8编组动车组和16遍组动车组的头车当量泄漏面积一样时,8编组动车组头车内每10 s的最大压力变化量的最大负压值却比16编组的大。所以8编组和16编组动车组以380 km/h的速度通过1 097 m隧道,当头车内压力同时满足1 000 Pa/10 s标准时,8编组动车组的头车当量泄漏面积阈值必然要小于16编组的,符合图 9(a)中蓝色点划线变化趋势。 (a) 车外压力 (b) 车内每10 s内最大压力变化量 表5统计了不同编组单列动车组以380 km/h速度通过京沪线长度大于500 m的10个隧道,车内压力符合三种不同舒适性标准的当量泄漏面积阈值的最小值。由表 5可知:16编组动车组符合800 Pa/3 s和1 000 Pa/10 s两个压力舒适性标准时的当量泄漏面积阈值的最小值小于8编组的;而8编组动车组符合500 Pa/s压力舒适性标准时的当量泄漏面积阈值的最小值小于16编组的。 表5 不同编组单列动车组当量泄漏面积阈值的最小值 图11表示16编组动车组以300 km/h、350 km/h、380 km/h和400 km/h四种速度通过2 812 m隧道,车内压力符合1 000 Pa/10 s标准时的当量泄漏面积阈值随车速的变化规律。由图 11可知:当量泄漏面积阈值随着车速的增加而减小;中间车的当量泄漏面积比头尾车的大。以中间车为例,动车组速度从350 km/h增加到400 km/h,动车组速度增加了14.3%,当量泄漏面积阈值从35.6 cm2减小到28.0 cm2,当量泄漏面积阈值反而减小了21.3%;动车组速度为350 km/h时,中间车的当量泄漏面积阈值比头车和尾车的分别大41.3%和94.5%。 图12表示16编组动车组以300 km/h、350 km/h、380 km/h和400 km/h四种速度通过595 m、1 097 m、1 504 m和1 905 m四个不同隧道,车内压力符合1 000 Pa/10 s舒适性标准时,头尾车和中间车当量泄漏面积阈值变化曲线。由图12可知:在符合车内压力舒适性标准的条件下,动车组以不同速度通过同一隧道,车速越高车厢当量泄漏面积阈值越小。 图11 当量泄漏面积阈值随动车组速度变化规律 表6统计了单列16编组动车组以四种不同速度通过京沪线长度大于500 m的10个隧道,车内压力符合三种不同舒适性标准的当量泄漏面积阈值的最小值。由表 6可知:满足三种不同压力舒适性标准的当量泄漏面积阈值的最小值均随着动车组速度的增加而减小。 (a) 头车 (b) 中间车 (c) 尾车 图13表示16编组动车组以400 km/h的速度单列车通过和隧道中央等速交会通过1 097 m、1 504 m、1 905 m和2 812 m四个不同长度隧道,车内压力符合1 000 Pa/10 s标准时,头尾车和中间车当量泄漏面积阈值变化曲线。由图13可知:16编组以400 km/h的速度在四个隧道内中央等速交会时的当量泄漏面积阈值比单列车通过时的小。 表7统计了16编组动车组以四种速度中央等速交会通过京沪线上隧道长度大于900 m的7个隧道,车内压力符合三种不同舒适性标准的当量泄漏面积阈值的最小值。结合表6和表7的统计结果,表 8最终给出了16编组动车组在不同速度等级下以不同方式通过京沪线上部分隧道,车内压力符合不同压力舒适性标准时的当量泄漏面积阈值的建议值。由表 8可知:当量泄漏面积阈值的最小值随着车速的增加而减小,且四种速度下均在符合1 000 Pa/10 s舒适性标准时取得对应最小当量泄漏面积的建议值。 (a) 头车 (b) 中间车 (c) 尾车 表7 16编组动车组以不同速度在隧道中央等速交会当量泄漏面积阈值的最小值 表8 当量泄漏面积建议值 本文选用薄壁孔流动模型,建立“当量泄漏面积法”,基于车内压力舒适度标准,以京沪线隧道为背景,研究了中国某型号标准动车组的单节车厢动态当量泄漏面积气密阈值,得出以下结论: (1) 通过与试验数据对比,说明本文所建立的“当量泄漏面积法”计算车内压力的合理性及程序的准确性。 (2) 单列16编组动组以350 km/h的速度通过隧道长度大于500 m隧道时,当量泄漏面积阈值的最小值按符合500 Pa/s、800 Pa/3 s和1 000 Pa/10 s标准依次减小。 (3) 单列8编组和16编组动车组以380 km/h的速度过通过隧道长度大于500 m隧道时,在满足800 Pa/3 s和1 000 Pa/10 s压力舒适性条件下,16编组的当量泄漏面积阈值的最小值比8编组的小。 (4) 16编组动车组以不同速度通过隧道长度大于500 m隧道时,当量泄漏面积阈值的最小值随着车速的增加而减小。 (5) 16编组动车组以中央等速交会的方式通过隧道长度大于900 m隧道时当量泄漏面积阈值的最小值比单列车通过时的小。 (6) 动车组车速400 km/h,符合1 000 Pa/10 s舒适性标时头/尾车和中间车当量泄漏面积最严格分别为10.3 cm2和18.9 cm2。1.4 统计不同时间间隔内最大压力变化量方法

1.5 车厢当量泄漏面积阈值确定方法

1.6 验 证



2 计算结果及分析
2.1 计算参数及舒适性标准


2.2 车内外压力波形成机理



2.3 舒适性标准的影响特性






2.4 编组长度的影响特性






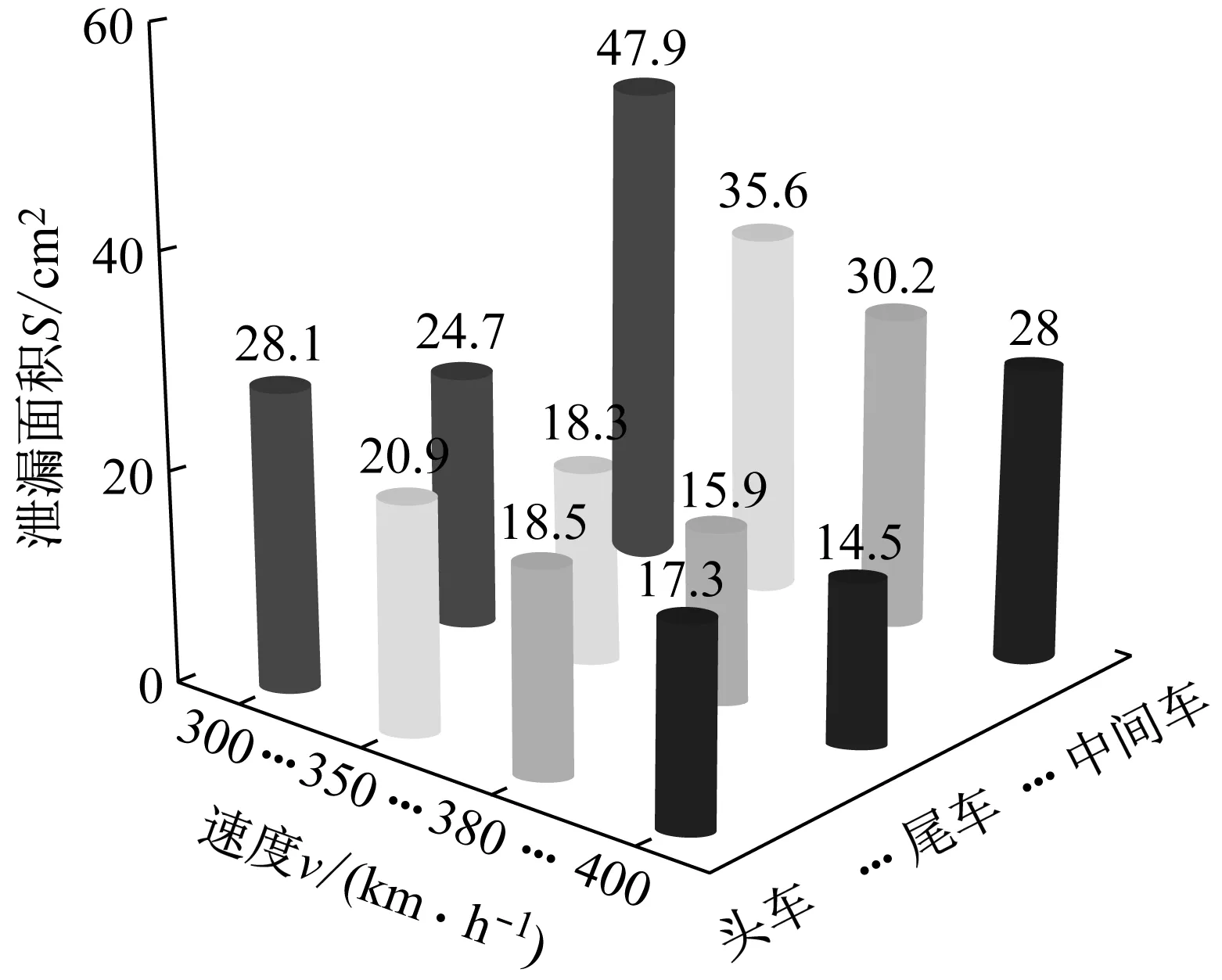
2.5 速度的影响特性



2.6 单列车过隧道与两列车隧道交会对比





3 结 论

