一种新型异形椭圆隧道横断面的性质及优化设计

武 周 虎

(青岛理工大学 环境与市政工程学院，山东 青岛 266033)

0 引 言

随着国内外交通基础设施的快速发展，各种隧道工程建设的规模和数量日益增大。由于缺乏合适的已知曲线方程，现行隧道横断面的内轮廓线除采用单心圆(含椭圆)外，主要由三心圆[1]、四心圆[2]、五心圆[3]等多圆弧拼接而成，还有直壁边墙，既有尖拱，也有坦拱，隧道内轮廓线形状及尺寸可谓种类繁多[4-6]。对于不同的围岩稳定性和山岩压力条件，要使结构支撑的作用力最小，隧道横断面的最佳宽高比应等于地应力比值的平方根[7]；对于公路隧道，还需要根据道路等级、车道数、车型、车速、单/双向行驶等条件确定建筑限界范围，进行隧道横断面形状、开挖、结构和衬砌施工等设计[8,9]。

由于围岩的介质材料和初始地应力场等边界条件是不能改变的客观存在，所以在设计过程中，可通过改变施工步序、支护手段、衬砌参数，及调整洞室断面的几何形状及尺寸等措施，来改善围岩应力分布，确保围岩稳定。隧道横断面形状设计方案不是唯一的，有许多方案可供选择，这就有个优化问题[10]。要科学合理确定各个圆心的位置、半径和圆心角，将建筑限界完全包容在内轮廓线内，使几段圆弧画出来的闭合误差最小，且绘图与优化设计快捷、方便，目前尚缺乏设计与建造的统一标准。仅以四心圆隧道横断面的内轮廓线为例，就有半径r1、r2、r3和圆心角φ1、φ2或切点高度h1、h2共5个独立变量[11]；各种类型隧道横断面几何形状和尺寸的优化设计方法更是繁多复杂[12,13]。由多圆弧或直线段拼接而成的隧道横断面内轮廓线，连接点(切点)处虽然能满足曲线的连续光滑，但其1阶导数不光滑，2阶导数不连续，出现曲率突变现象，受力条件变差[14]。寻求一种科学合理的隧道内轮廓线方程是解决这个问题的根本途径。

笔者基于宽阔河流中心稳定点源条件下的保守物质等浓度线方程，以隧道横断面内轮廓线的最大高度和最大宽度为参数，定义了一种新型Wu’s曲线——异形椭圆，给出了异形椭圆的标准方程；分析了异形椭圆横断面的几何性质及分类，提出了异形椭圆隧道横断面的优化设计方法。研究结果可为异形椭圆隧道横断面设计提供理论支持。

1 异形椭圆方程的由来与标准化

1.1 异形椭圆方程由来

在宽阔河流中心稳定点源条件下，保守物质平面二维对流扩散简化方程的浓度C(x,y)分布如式(1)[15]：

(1)

式中：x为自排放口沿河流流向的纵向坐标；y为垂直于x轴的横向坐标，坐标原点取在河流中心排放点；d为河流的平均水深；U为河流的平均流速；m为单位时间保守物质的排放质量；Ey为横向扩散系数。

武周虎等[16]在保守物质浓度C(x,y)=Ca(常数)条件下，对式(1)进行了数学推演，给出了等浓度线所包围图形的最大长度Ls、最大半宽度bs和最大半宽度对应的纵向坐标Lc分别为：

(2)

(3)

(4)

式中：e为数学常数，e≈2.718；其它符号同前。

令式(1)中浓度C(x,y)=Ca，将分母根号下的纵向坐标x除以Ls，得到归一化纵向坐标(x/Ls)，再乘以式(2)等号右边的纵向最大长度表达式；对式(1)中exp()的横向坐标y除以bs得到归一化横向坐标(y/bs)，再乘以式(3)右边的横向最大半宽度表达式。整理得到保守物质归一化等浓度线(Wu’s曲线)方程[17,18]：

(5)

式(5)反映的是一种由最大长度和最大半宽度所表示的二参数曲线，近似于椭圆形状，但只有单对称轴x。笔者将其定义为“异形椭圆”。该曲线来源于保守物质平面二维对流扩散简化方程求解出来的浓度分布等值线，根据动量、热量和质量传递的相似性原理，可以推断应力与质量扩散之间也存在相似性关系。因此，该曲线极具研究价值。

1.2 标准方程及几何特征分析

将式(5)中的对称轴纵向坐标x改用对称轴纵向坐标z表示，坐标原点设在隧道横断面内轮廓线底部中点处。定义异形椭圆对称轴纵向坐标z向上的最大高度为H=Ls，表示隧道横断面高度；非对称轴横向坐标y方向的最大宽度为W=2bs，表示隧道横断面宽度。则，有异形椭圆隧道横断面内轮廓线的标准方程：

(6)

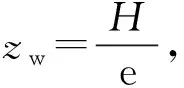
表1及图1分别为异形椭圆式(6)与青岛胶州湾海底隧道(单向3车道)横断面[2]及某高速公路隧道(单向2车道)横断面[5]的参数及内轮廓线对比。

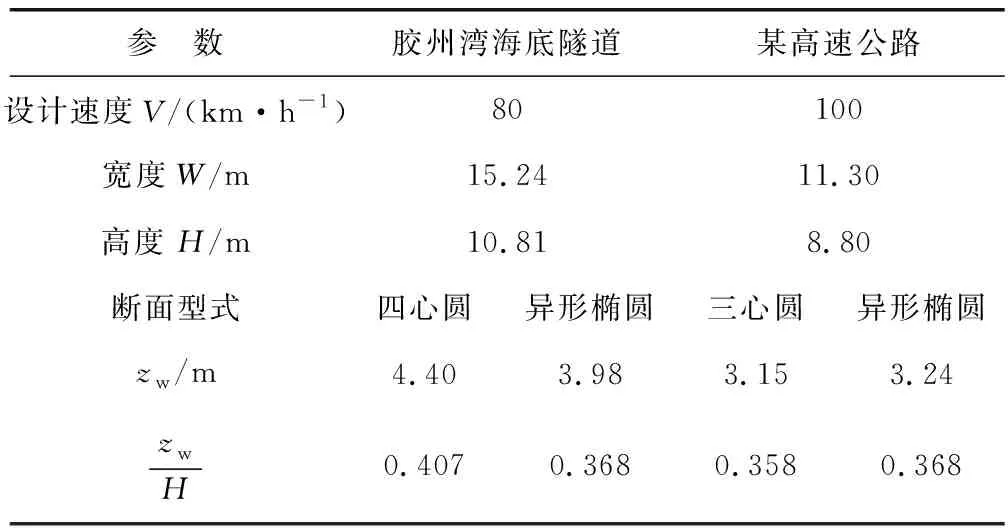
表1 异形椭圆与隧道内轮廓线特性参数Table 1 Characteristic parameters of heteromorphic ellipse and tunnel inner outline

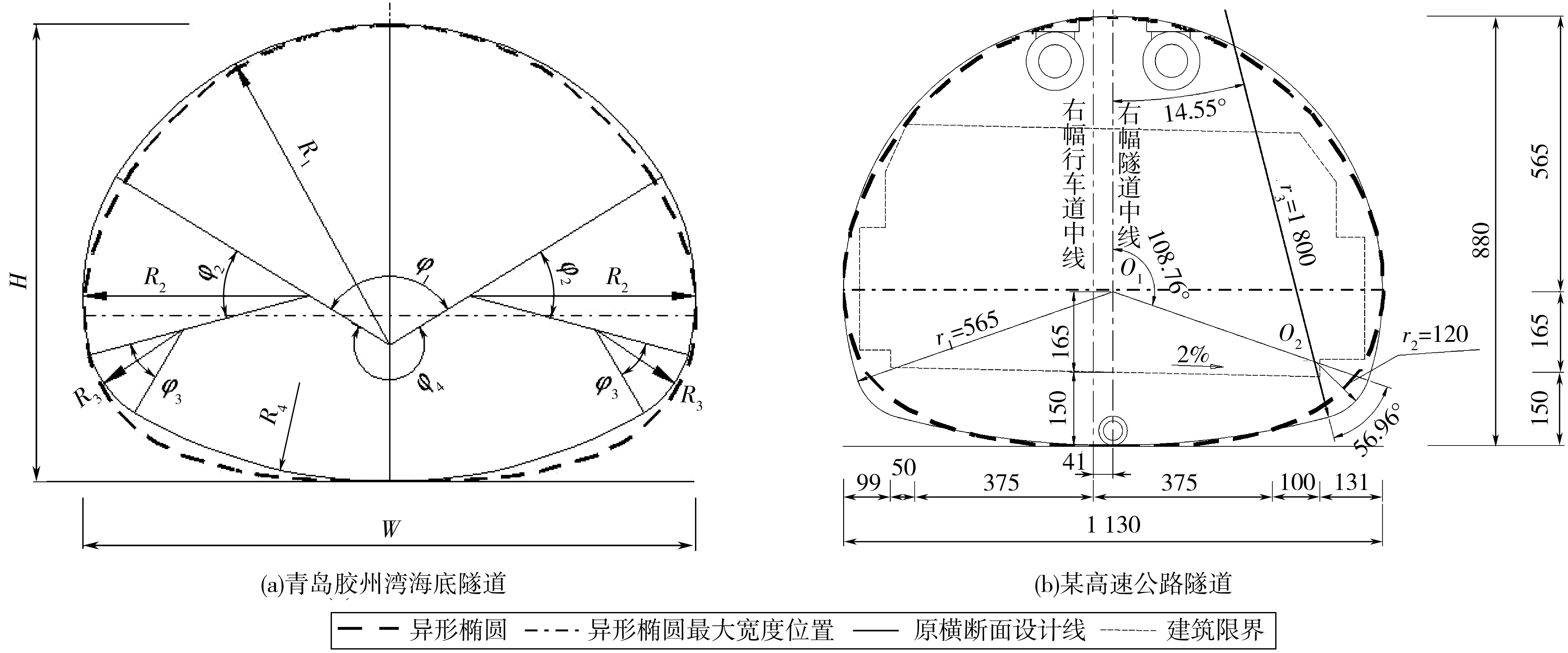
图1 异形椭圆与隧道横断面内轮廓线(单位：cm)Fig. 1 Heteromorphic ellipse and inner outline of tunnel cross-section

由表1及图1可以看出：

1)异形椭圆与青岛胶州湾海底隧道四心圆横断面内轮廓线吻合较好，主要差别出现在隧道横断面的仰拱部位。异形椭圆的仰拱更加平坦，横断面最大宽度相应的纵向位置坐标zw下移，有利于建筑限界的整体布置下移，可以减少路基底下的回填工程量。

2)异形椭圆与某高速公路隧道三心圆横断面内轮廓线吻合较好，主要差别出现在隧道横断面的拱脚部位。

鉴于异形椭圆与三心圆、四心圆隧道横断面内轮廓线吻合较好，笔者创造性提出异形椭圆(即Wu’s曲线)隧道横断面内轮廓线形状。

2 异形椭圆的几何性质

2.1 面 积

将式(6)等号两边开平方根，再同乘以W。由于异形椭圆的单轴对称性，在z∈[0，H]区间上对2y(z)求定积分，则，异形椭圆面积S按式(7)计算：

(7)

进行变量替换，令z/H=ζ，积分上限变为1，则有

(8)

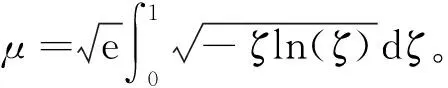
可见，异形椭圆面积等于异形椭圆面积系数、高度和宽度的乘积。

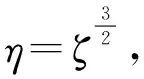
(9)

(10)

2.2 形心坐标

形心即异形椭圆的几何中心。对于密度均匀的实物体，形心与质心重合。对于只有单对称轴的异形椭圆，形心一定在其对称轴上，但需要通过对非对称轴面积矩的计算来确定具体位置。根据总面积矩等于各分面积矩之和的原理，有：

(11)

(12)

(13)

因此，异形椭圆的形心位于对称轴上相对高度坐标z′c=zc/H≈0.465处，该处的高度低于中位线(即异形椭圆半高度)的7.05%。

2.3 压缩系数θ及形状分类

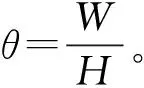
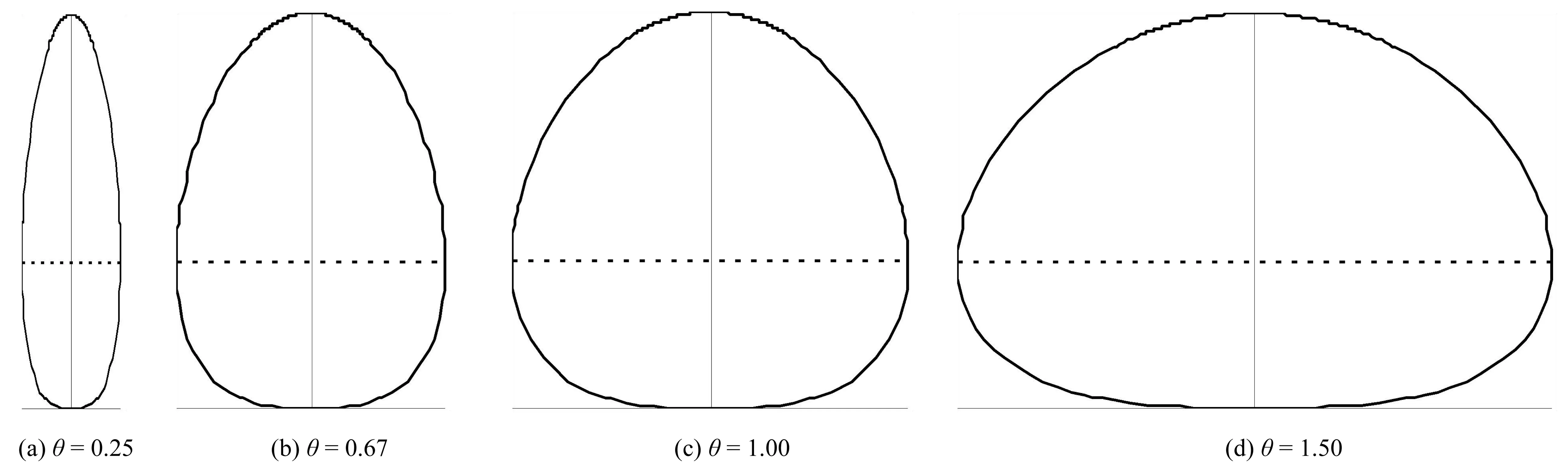
图2 不同压缩系数θ的异形椭圆Fig. 2 Heteromorphic ellipse with different compression coefficient θ

由图2可以看出，当压缩系数θ由小到大变化时，异形椭圆的形状由高瘦向宽胖变化，更像一个自然图形，如：图2(a)形似玉米棒，图2(d)形似面包形状，而图2(b)、(c)形似梨、桃、苹果等形状。由此得到，压缩系数θ可以反映异形椭圆的形状变化特征。因此，可按压缩系数θ对异形椭圆形状进行分类，如表2。

表2 基于压缩系数θ的异形椭圆形状分类Table 2 Shape classification of heteromorphic ellipse based on compression coefficient θ

2.4 周 长

根据高等数学平面曲线弧长的积分定义，异形椭圆的周长L积分式为：

(14)

对式(6)两边求导，整理得到：

(15)

令ζ=z/H，且θ=W/H，将式(15)代入式(14)，得：

(16)

式中：Th为异形椭圆系数。

参照椭圆的周长定理，由式(16)定义异形椭圆的周长定理：异形椭圆的周长L等于异形椭圆系数Th与异形椭圆半宽度W/2和半高度H/2之和的乘积。

由异形椭圆系数的表达式可以看出，异形椭圆系数Th只是压缩系数θ的函数。在[0.01，100]区间上给定一系列θ值，采用数值积分方法，对异形椭圆系数进行数值积分运算，得到一系列相应的Th或θ值，从而可得异形椭圆系数与压缩系数的关系曲线。图3为在相同条件下异形椭圆系数及椭圆系数(摘自数学手册)与压缩系数θ的关系曲线。

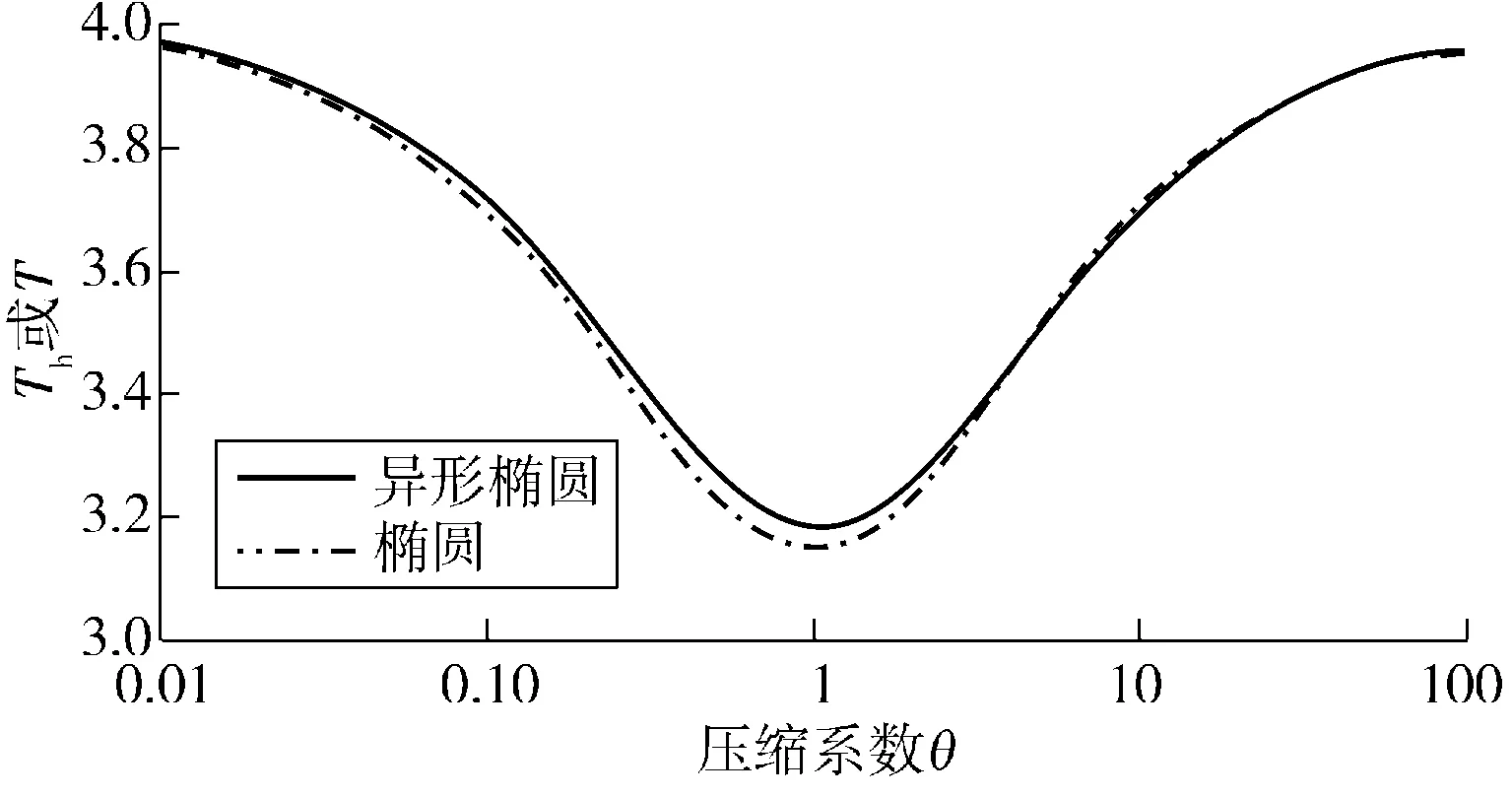
图3 异形椭圆系数Th及椭圆系数T与压缩系数θ的关系曲线Fig. 3 Relation curves of heteromorphic elliptic coefficient Th,elliptic coefficient T and compression coefficient θ

由图3可以看出：

1)椭圆系数T关于对数坐标压缩系数θ=1左右对称，即在宽高比与高宽比相等条件下，椭圆系数相等。

2)在压缩系数θ相同的条件下，异形椭圆系数Th与椭圆系数T存在以下3种关系：①Th>T；②当2种椭圆的θ→ 1时，Th与T的相对差值较大；③当2种椭圆的θ< 0.1或θ> 10时，Th与T的相对差值较小。

3)θ=1时，异形椭圆为标准型，异形椭圆系数Th=3.191 244，椭圆系数T=π，Th比T大1.58%；标准型异形椭圆的面积系数μ异形椭圆/Th=0.249 227，该值仅比圆的面积系数μ圆/π小-0.31%，说明标准型异形椭圆具有周长一定条件下面积近似最大的特点。

4)一个有趣的现象是：异形椭圆系数的最小值Th,min=3.190 820出现在压缩系数θ=1.05处，而不是在θ=1处。当θ< 1.05时，Th随着θ的增大而单调下降；θ>1.05时，Th随着θ的增大单调上升。

2.5 曲率半径ρ

曲率表示曲线在某一点的弯曲程度，曲率越大，曲线的弯曲程度越大。曲率的倒数为曲率半径，异形椭圆的曲率半径ρ与其形状(压缩系数θ)和尺寸大小密切相关。在θ相同条件下，异形椭圆尺寸越大，曲线上相应点的ρ越大，曲线的弯曲程度越小。

(17)

(18)

(19)

曲率半径公式如式(20)：

(20)

考虑到异形椭圆的单轴对称性，绘制出半边y、y′、y″及ρ曲线进行分析，如图4。

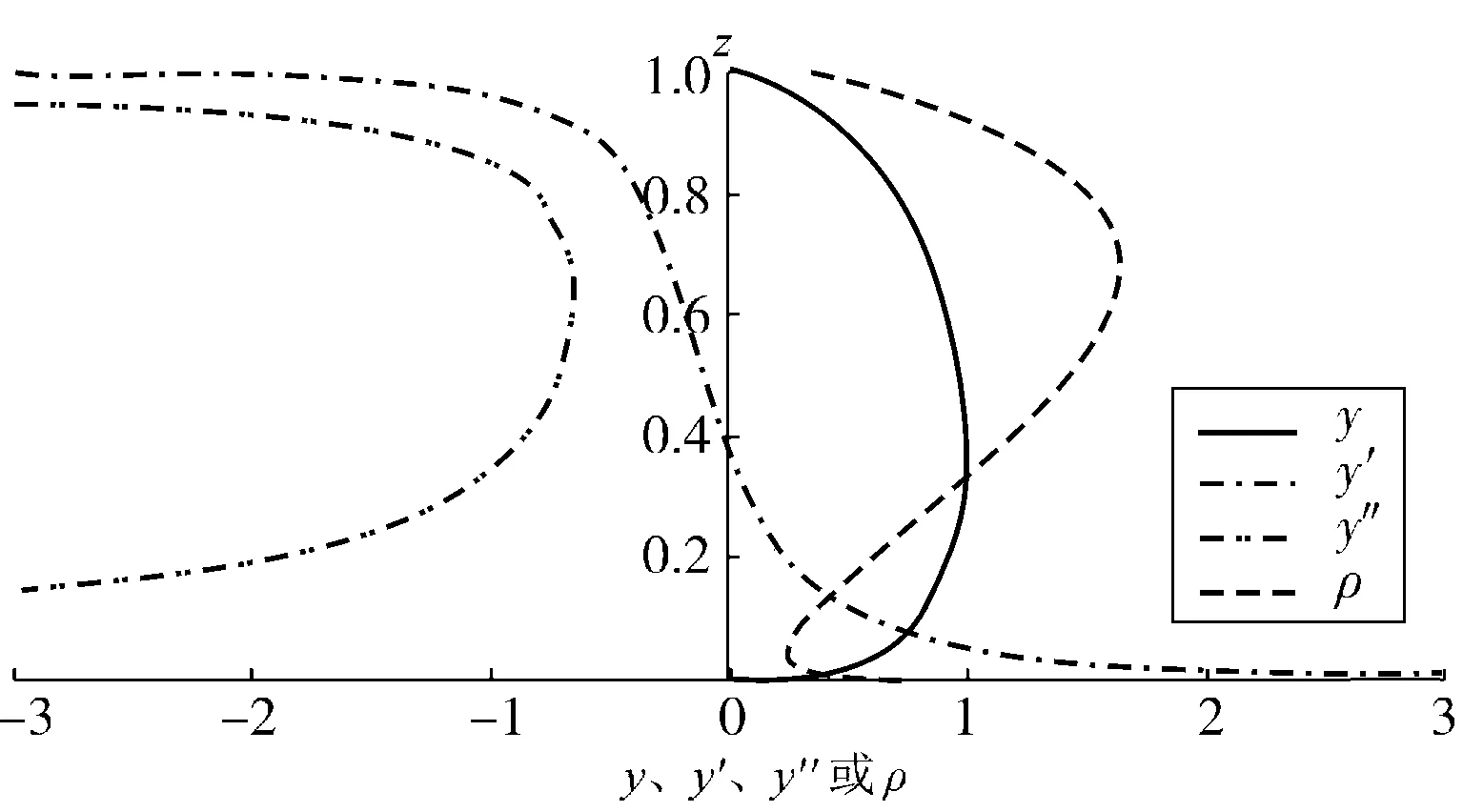
图4 单位标准型异形椭圆半边y、y′、y″和 ρ曲线 Fig. 4 Half curves of unit standard-type heteromorphic ellipse y, y′, y″ and ρ

由图4可以看出：

1)在(0，1)区间上，单位标准型异形椭圆y=f(z)存在1阶、2阶连续导数，表明异形椭圆和1阶导数曲线均为光滑曲线。

2)在[0，1]区间上，单位标准型异形椭圆的ρ是连续变化的，ρ随着z变化的函数曲线呈“2”字形变化，即：当z→0时，ρ→∞；随着z的逐渐增大，ρ迅速减小，当z=0.0427时，ρ达到极小值ρmin=0.248 2；随后，随着z的增大，ρ逐渐增大，当z=0.677 9时，ρ达到极大值ρmax=1.645 7；之后，随着z的增大，ρ再次减小，当z=1.000 0时，ρ=0.339 8。

3)需要注意的是，在异形椭圆压缩系数θ和尺寸大小不同的情况下，曲率半径ρ随着z变化的函数曲线仍然具有“2”字形变化规律，只是ρ的数值和极值点位置发生了改变。

3 异形椭圆横断面的优化设计方法

3.1 建筑限界控制点几何关系

在JTG D 70—2004《公路隧道设计规范》的单向公路隧道建筑限界与控制点详图中，添加坐标系和各控制点编号，取隧道中线与异形椭圆对称轴z重合，车道中线上路面点坐标(z0，y0)，如图5，图中：H0为建筑限界高度；W0为行车道宽度；H1为检修道或人行道空间高度；H2为建筑限界顶角下缘高度；LL、LR为左、右侧向宽度；C为余宽；J(R)为检修道(人行道)宽度；h为检修道或人行道的高度；EL、ER为建筑限界左、右顶角宽度；i为隧道路面横坡；hw为通风机、内装设备等安装所需的隧道中线最小高度。

在图5中隧道横断面建筑限界各控制点编号k=Ⅰ，Ⅱ，Ⅲ，…，n；控制点数n=9。当自然通风量可以满足隧道通风需要时，可不设Ⅸ号控制点，此时控制点数n=8。

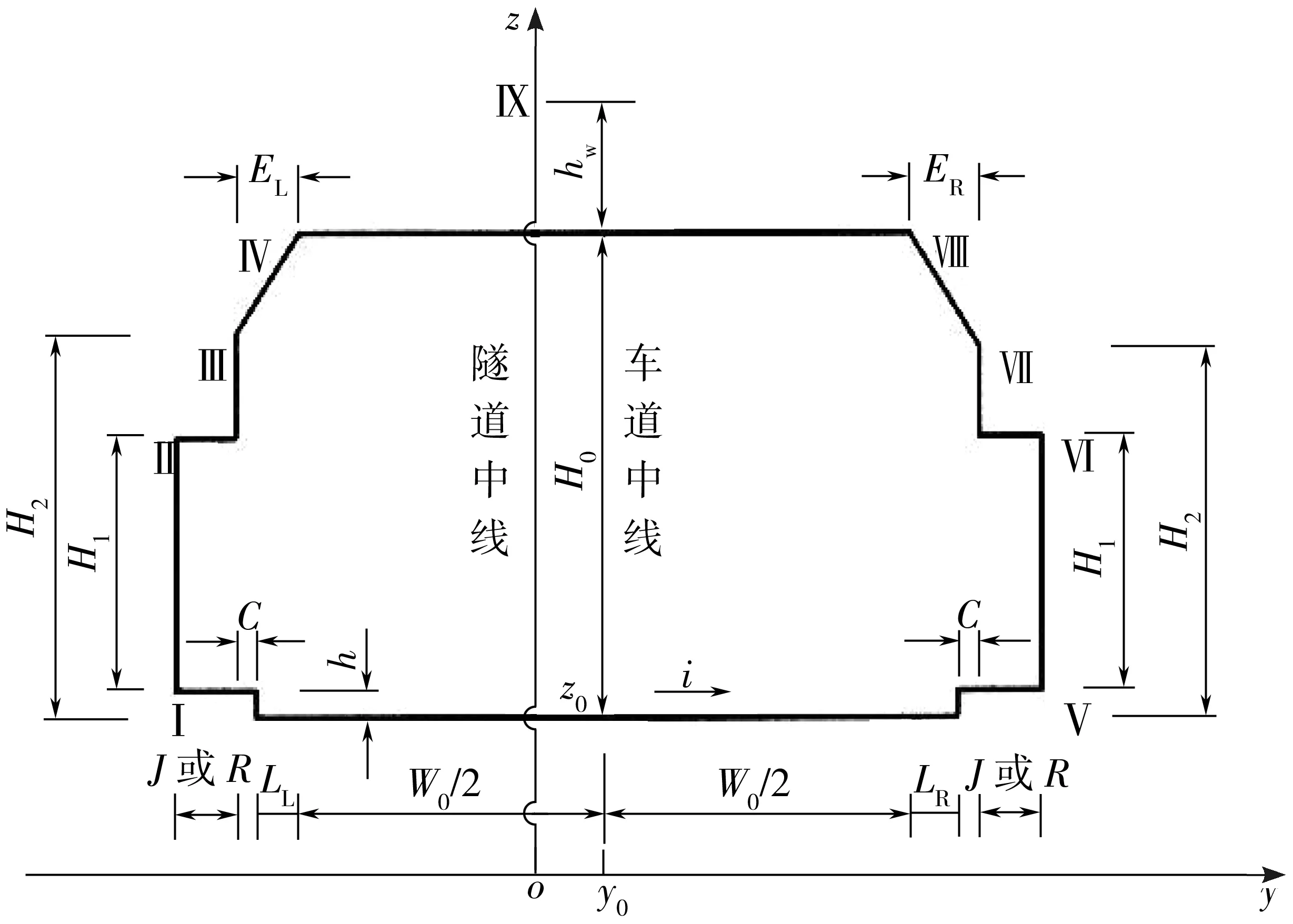
图5 建筑限界与控制点Fig. 5 Construction clearance and control point

3.2 建筑限界控制点坐标表达式

根据图5中隧道建筑限界控制点的几何关系，可推算得到各控制点的坐标表达式，见表3。

转化运作机制还没有有效形成 目前，学校虽然制定了科技成果转化、专利的管理办法，提出科技成果转化实施中，学校和课题组的股份或收益分配比例基本为30:70，但是就目前来看，对科技成果价值进行评估这方面的办法确实存在缺陷。对科技成果价值评估本身的难度很大，评估低了会涉及国有资产流失，评估高了会没有市场。在科技成果转化过程中，科技成果价值评估可以说是一个非常重要且关键的问题，同时是进行有效转化的必要环节。然而关于科技成果价值评估办法，不是随便就可以制定的，而是需要由国有资产管理、计财以及科技等部门来联合进行制定。

表3 建筑限界控制点坐标表达式Table 3 Coordinate expression of construction clearance control points

由表3可以看出，建筑限界各控制点的纵向坐标z和横向坐标y表达式为车道中线上路面点坐标(z0，y0)和几何尺寸的函数。前者路面中线点的坐标由优化计算确定，后者建筑限界的各几何尺寸由道路等级、车道数、车型、车速、单双向行驶等设计条件，根据JTG D 70—2004《公路隧道设计规范》的要求确定。

3.3 约束条件与目标函数

由式(6)变形得到异形椭圆的显函数方程：

(21)

为了达到建筑限界的任何点均在异形椭圆之内的设计要求，异形椭圆至少应将建筑限界完全包容在内，即异形椭圆必须套进隧道横断面建筑限界各控制点。图6为异形椭圆与建筑限界对应控制点示意。

图6 异形椭圆与建筑限界对应控制点示意Fig. 6 Control points corresponding to heteromorphic ellipse and construction clearance

图6中，在纵向坐标z相同的条件下，异形椭圆上与建筑限界对应的控制点编号依次为k′=Ⅰ′、Ⅱ′、…、Ⅸ′)。要达到隧道洞室净空面积最小的目标，就应该使得满足建筑限界的异形椭圆面积最小。

目标函数是评价设计方案好坏的标准。一般而言，目标函数可以表示为问题变量的解析表达式。目标函数可以是一个，也可以是多个，但应尽量使目标函数的数目少一些。对异形椭圆隧道横断面内轮廓线进行优化，可选择满足约束条件的单目标函数优化算法，其约束条件和目标函数的确定如下：

设异形椭圆与建筑限界各对应控制点的水平距离为dk，为确保异形椭圆上对应控制点在建筑限界控制点之外或重合，要求dk≥ 0，即

dk=|f(zk)|-|yk|≥0，(k=Ⅰ，Ⅱ，Ⅲ，…，n)

(22)

以隧道洞室净空面积最小为目标，根据异形椭圆的面积式(8)，可得到目标函数

S=min(μWH)=μmin(WH)

(23)

3.4 优化计算

异形椭圆隧道横断面的优化计算分为3种情形：①控制点数n=9；②控制点数n=8或9，给定隧道横断面宽高比W/H，即异形椭圆的压缩系数θ；③控制点数n=8，给定最大宽度W或最大高度H限定值。针对这3种情形，在对应的给定条件下，同时满足约束条件式(22)，采用目标函数优化算法——传统优化算法或智能优化算法进行异形椭圆隧道设计，设计步骤如下：

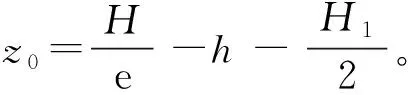
2)运行单目标函数优化算法程序(如MATLAB数学实验室)进行优化计算。

3)根据优化计算结果，即目标函数式(23)的最小值，给出异形椭圆隧道横断面的宽度W和高度H及车道中线上路面点坐标(z0，y0)。

4 设计实例

某双向四车道高速公路穿山隧道工程，采用分离式独立双洞设计方案，设计时速80 km/h[5]。隧道单洞右幅行车道的建筑限界形状如图5，限界尺寸为：H0=500 cm，W0=750 cm，H1=250 cm，H2=400 cm，LL=50 cm，LR=75 cm，C=25cm，J(R)=50 cm，h=35 cm，EL=50 cm，ER=75 cm，i=0.015，hw=200 cm。建筑限界最大范围为1 025 cm× 500 cm，考虑通风机、内装设备等安装所需的隧道中线最小高度，控制点数n=9。

在设计实例中，异形椭圆隧道横断面的优化计算属于3.4优化计算中的情形①，控制点数n=9。

根据表3中控制点坐标表达式进行计算，化简得到该隧道工程建筑限界控制点坐标和由式(21)计算得出的异形椭圆对应控制点坐标函数，如表4。

表4 建筑限界与异形椭圆对应控制点坐标及优化结果Table 4 Coordinate of control point corresponding to the construction clearance and heteromorphic ellipse and optimization results

在表4中，取隧道三心圆横断面[5]的最大宽度和最大高度作为异形椭圆优化计算的初始宽度和高度W=1 100 cm和H=825 cm，有z0=143.500 cm，取y0=0，使优化计算的收敛过程更快。

在约束条件式(22)条件下，运行单目标函数优化算法程序，求目标函数式(23)的最小值。经过优化计算和设计参数取整，最后得到满足约束条件的异形椭圆与建筑限界各对应控制点水平距离ds的优化计算结果见表4(右列)，目标函数最小值为S=728 021 cm2，相应的异形椭圆隧道横断面优化设计参数为最大宽度W=1 110 cm和最大高度H=825 cm，车道中线上路面点坐标(z0=121 cm，y0=-17 cm)。

据此绘制满足设计条件的异形椭圆隧道横断面内轮廓线，见图7，同时绘出三心圆内轮廓线，以进行比较。图中：r1=550 cm，圆心坐标(x1,y1)=(275，0)，圆心角φ1=2×103°45′24″；r2=120 cm，圆心坐标(x2,y2)=(172.7，±417.7)，圆心角为φ2=61°50′53″的两段圆弧；r3=1 800 cm，圆心坐标(x3,y3)=(1 800，0)，圆心角φ3=2×14°23′43″。

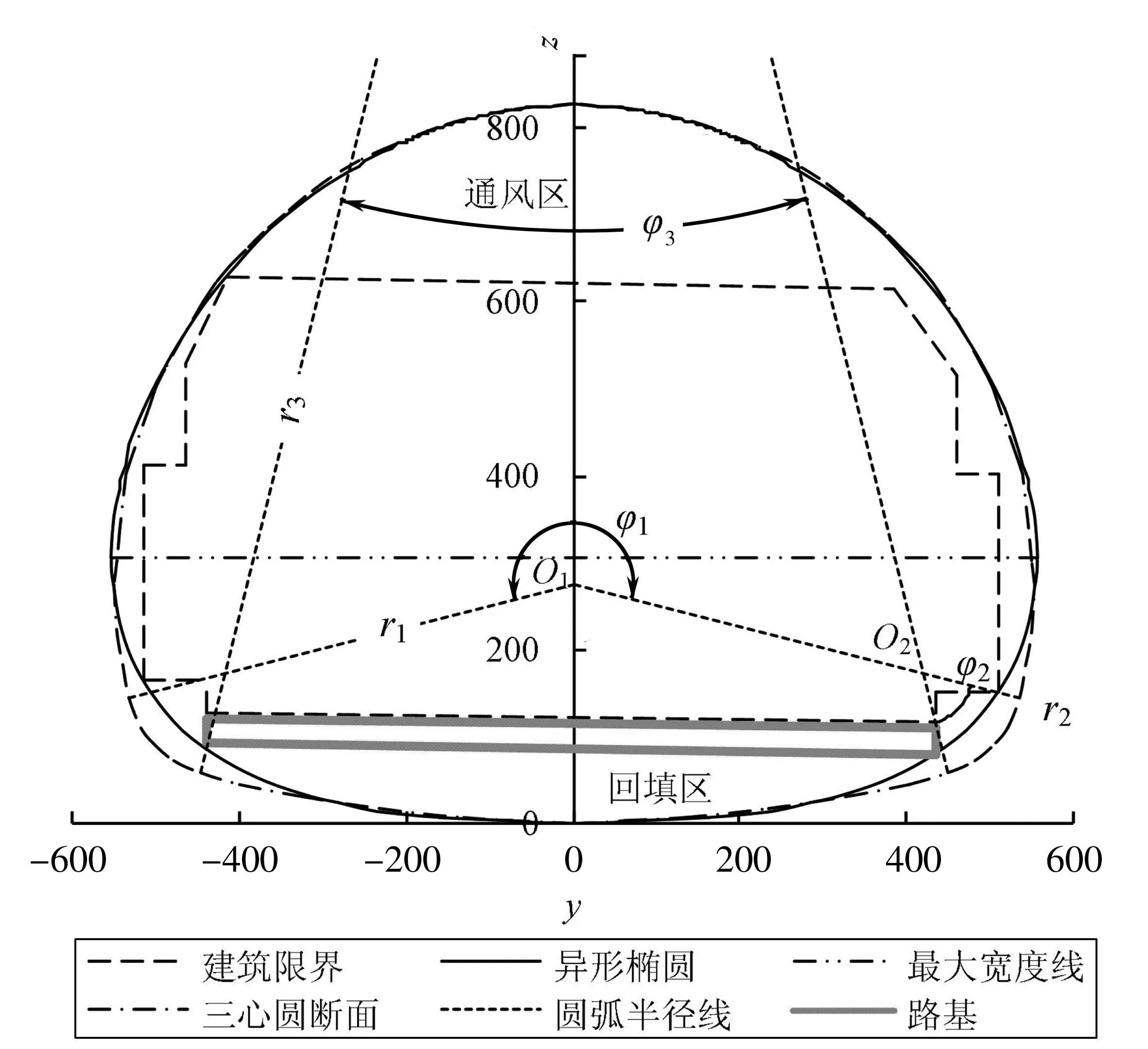
图7 异形椭圆与三心圆隧道横断面(单位:cm)Fig. 7 Tunnel cross-section of heteromorphic ellipse and three centered circle

由图7和表4中的优化结果可知，单洞右幅行车道建筑限界的主要约束为Ⅰ、Ⅳ和Ⅴ号控制点。在设计参数取整后，建筑限界上这3个控制点外侧与异形椭圆对应控制点的水平距离均为1 cm；满足通风机、内装设备等安装所需的隧道中线最小高度的Ⅸ号控制点在z轴上zⅨ=821 cm处，即Ⅸ号控制点顶部与异形椭圆最高点的垂直距离为4 cm。总体来看，经过优化计算所得到的异形椭圆与建筑限界的符合程度高。

将异形椭圆与三心圆隧道横断面进行对比发现：

1)与三心圆相比，异形椭圆横断面内轮廓线的宽度增大10 cm，面积减小12 414 cm2(三心圆面积为740 435 cm2)，高度相同。表明，异形椭圆可节省隧道洞室净空土石方量1.68%。

2)异形椭圆的压缩系数θ=W/H=1.35，由图3可得异形椭圆系数Th=3.20，由式(16)可计算得到异形椭圆的周长L=3 096 cm，而三心圆周长为3 156 cm。表明，异形椭圆可节省隧道洞室支护与衬砌施工材料1.90%。

3)异形椭圆的1阶、2阶连续导数均存在，曲率半径呈现连续变化规律，而三心圆横断面的3个曲率半径在连接点(切点)出现突变现象，受力条件差。

4)由图7可以看出，异形椭圆上部与三心圆横断面大致吻合，下部克服了三心圆横断面的拱脚外凸现象，可节省仰拱开挖和回填工程量。

5)异形椭圆横断面只需要2个设计参数，相比三心圆横断面需要4个独立参数，优化设计更加便捷，且易于掌握和误差控制。

5 结 论

1)基于河流二维对流扩散物质的等浓度线方程，定义了一种新型二参数异形椭圆内轮廓线方程，给出了异形椭圆面积、周长、形心坐标、压缩系数和曲率半径的计算公式；对异形椭圆进行了形状分类：标准型(θ=1)，H型(0<θ<1)，W型(θ>1)。

2)异形椭圆的面积等于异形椭圆面积系数、高度与宽度的乘积；周长等于异形椭圆系数与异形椭圆半高度和半宽度之和的乘积。

3)根据单向公路隧道建筑限界，给出了控制点坐标表达式；按照将建筑限界完全包容在内和隧道洞室净空面积最小的原则，提出了异形椭圆横断面的约束条件、目标函数和优化设计方法。

4)异形椭圆与建筑限界的符合程度高，与三心圆横断面相比，异形椭圆具有设计参数少、曲率半径变化连续、隧道洞室净空面积小、支护与衬砌周长短、仰拱开挖和回填工程量小等优点。