基于位移影响矩阵的高铁站房混凝土框架结构预应力损失计算方法

曾 月,丁 峰,赵一超,卓 彪,刘艳辉

(西南交通大学土木工程学院,成都 610031)

引言

铁路客站是铁路网的重要节点，其健康监测问题已经引起了铁路管理部门和设计部门的重视。2012年，原铁道部发《关于印发<铁路客站雨棚专项整治会议纪要>的通知》(铁鉴函[2012]522号文)中指出“建设司、鉴定中心牵头组织大型客站结构健康监测系统设置标准与工程方案的研究，当前客站工程建设的结构健康监测系统，应在工程设计中尽快明确并实施”；最新颁布实施的TB10621—2014《高速铁路设计规范》[1]第20.2.22条要求：特大型站房结构宜进行整体结构健康监测。

预应力混凝土结构为大跨、超长、重载、防裂等工程难题提供了解决思路和技术方案；高铁主站房一般采用框架结构，受市政地铁和国铁布置及使用功能的影响，结构跨度很大，因此，预应力混凝土结构成为主要采用的设计手段之一；在西南交通大学统计的60个大型站房统计样本中，预应力混凝土楼层所占的结构类型比例为56.7%，如图1所示。

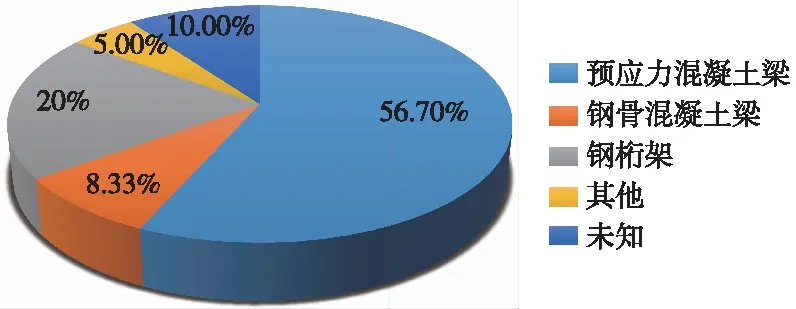
图1 站房结构统计

预应力损失是预应力混凝土结构必须直面的问题。随着时间的推移、环境的改变、结构的损伤老化等因素都会导致初始预加应力的损失，随着预应力损失值的逐步增加，抗力性能指标和安全度逐渐降低，结构可能存在一定的安全隐患和服役风险，需要一定的技术手段对预应力结构的使用功能及承载力状态进行跟踪[2]。针对预应力损失的计算，我国GB50010—2010《混凝土结构设计规范》[3]和JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[4]提出了计算方法和公式，但规范采用分项叠加法进行计算[5]，未考虑混凝土收缩、徐变与钢筋松弛三者的耦合，不能精确计算预应力损失。ACI 209—92[6]、CEB-FIP Model Code 90[7]等设计规范规定了能够预测结构受长期荷载的徐变和收缩模型，但它们只能预测平均值，不能得到即时的变化值[8]。并且，目前“桥建合一”站房结构体系是普遍采用的建筑形式，该类结构建于高架桥上，上部大跨度框架结构与高架桥的桥墩共用一个基础。当列车高速运行通过车站时会引起振动，振动荷载随之传递给上部结构，长期的振动使结构本身产生疲劳破坏[9]。疲劳损失也会使结构产生预应力损失[10]，但现阶段对该观点的研究还不完善，要对其进行理论计算较为困难。

因此，为保证结构的正常使用与安全性，对预应力混凝土结构的预应力损失进行定期检测尤为重要。针对预应力损失检测的问题，国内外很多学者提出了解决方法。一种是有损检测，该方法由曾丁[11]、Vimalanandam.V等[12]提出，利用SSRHT法对预应力混凝土梁中预应力损失进行估算。与之类似的有：用截面法[13]测钢筋的预应力值、打孔法[14]实测构件中的残余应力。但这类方法在现场实测时较为繁琐，且钻孔、切割取样产生的局部高温会影响测量精度，并对构件产生一定的损伤。另一种方法是无损检测，兰春光等[15-19]基于光纤光栅传感技术的特性，设计制作了能自监测预应力状态的智能钢绞线，并应用于实际工程中，但该类钢绞线与普通钢绞线相比，力学性能有所下降，施工较为繁琐，且引线在施工过程中有可能被损坏。孙志伟等人基于灰色预测理论，获得桥梁结构长期竖向预应力损失规律方法[20]，但该方法需长期采集数据，且未考虑桥梁运营过程中车辆荷载等因素导致的荷载不对称对竖向预应力损失的影响。

由于结构的变形易获取，且获取过程对结构无损，因此通过结构的变形来识别预应力损失的方法引起许多研究者的重视。基于影响矩阵法的概念[21]，袁卓亚[22]等提出了将长期变形监测数据用于评估桥梁结构真实预应力的思路，建立了桥梁长期挠度与有效应力间的关系方程，并用实际数据验证了方法的可行性；In Hwan Yang[23]将该方法用来预测PSC箱形预应力混凝土桥上，由混凝土的收缩徐变引起的预应力损失，并指出该方法能合理降低预测的不确定性。刘艳辉[24]以某高铁站房预应力混凝土桁架屋盖为研究对象，建立了桁架结构中观测点变形值与结构预应力损失的关系，提出了基于位移影响矩阵法的单榀桁架预应力损失识别方法。综上所述，该方法可有效便捷地检测预应力的损失，提高测量精度，且对结构无损。但针对不同的结构类型，影响矩阵的参数取值不同。迄今为止，广泛用于高铁站房的预应力混凝土框架结构还未出现一个方便无损且测量准确的方法来检测预应力损失。

本文针对某铁路站房大跨预应力混凝土框架结构(梁采用后张法)，基于影响矩阵法的概念，通过建立有限元模型的方式，提出计算预应力损失的方法。并通过该方法，分析单位预应力损失量取值对预应力损失识别结果的影响，得到建立位移影响矩阵时单位预应力损失量的最佳取值和位移监测点的选取位置。在此基础上研究预应力混凝土框架结构发生预应力损失时主次梁监测点发生位移的规律。

1 预应力损失识别矩阵方程

1.1 位移影响矩阵

构件中预应力钢筋的应力值减小，会引起结构构件的位移发生变化。文献[25]研究表明：以结构构件的变形为基础，引入影响矩阵建立预应力损失与构件变形值的关系，可识别出构件中预应力损失的大小及位置分布。

每根梁中的所有预应力筋发生的损失都一样，将梁中的预应力筋归为一组，依次编号1～m，选取梁跨中位置作为位移监测点并编号1～n。在MIDAS中，计算结构在正常使用条件下未发生损失时各监测点的位移D0=[d10d20…di0…dn0]T；然后计算结构在正常使用条件下发生设定损失时各监测点的位移，Dj=[d1jd2j…dij…dnj]T，将D0分别与Dj依次相减，就得到位移影响矩阵，记作

cij=di0-dij

(2)

其中，cij为编号为j的预应力筋组在发生设定单位预应力损失量时，引起的位移监测点i的位移变化值，1≤i≤n，1≤j≤m；di0为结构在正常使用条件下全部预应力筋组的应力为初始张拉值σcon时，编号i的位移监测点的位移值；dij为结构在正常使用条件下编号为j的预应力筋组发生设定单位预应力损失量，其他预应力筋组未发生预应力损失时，编号为i的位移监测点的位移值。

1.2 识别系数列向量

预应力筋组j实际发生的损失占初始张拉应力的比值为实际损失量，记作Pj%；a%为建立位移影响矩阵时选取的单位预应力损失量。定义识别系数xj=Pj%/a%，由识别系数组成的[X]=[x1x2…xj…xm]T就是识别系数列向量。

1.3 实测位移列向量

记录实测得到结构监测点的位移变化值，得到位移变化列向量[M]=[m1m2…mj…mn]T。

1.4 预应力损失识别过程

选取需要监测损失的梁和位移监测点并编号，根据2.1节计算出设定单位预应力损失量a%对应的位移影响矩阵[C]，与实测数据得到的位移变化列向量[M]，以及识别系数列向量[X]建立关系方程如式(3)所示

[C]n×m[X]m×1=[M]n×1

(3)

求解矩阵方程(3)，得到预应力损失系数列向量[X]=[x1x2…xj…xm]T。

在实际应用中，可能遇到结构的变形观测点数量与结构中预应力筋组编号不等的情况，即m≠n，形成的影响矩阵为奇异矩阵，用常规解联立方程组的方法难以实现结构中预应力损失矩阵具体数值的求解。本文中预应力损失识别矩阵的求解采用最小二乘原理，通过构建式(4)和式(5)辅助函数，并利用MATLAB进行计算，其中令该函数取最小值的解(x1，x2，…，xm)即为结构中的预应力损失识别系数。

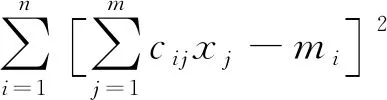
(4)

(k=1，2，…，m)

(5)

得到式(3)的解[X]=[x1x2…xm]T后，由公式(6)计算结构中预应力筋组损失值占初始张拉值的百分比。

Pj%=xj×a%

(6)

2 位移影响矩阵中参数的选取

2.1 位移监测点的选取原则

为确定框架梁中位移监测点的选取原则，以某单榀框架为例，对后张拉梁发生预应力损失时梁上不同位置位移变化进行计算。该预应力混凝土梁采用C40混凝土；预应力筋采用低松弛钢绞线，曲线布筋，直径为15.2 mm，抗拉强度fptk=1 860 MPa，张拉控制应力σcon=0.75fptk=1 395 MPa，采用一端张拉方式进行张拉，普通钢筋为HRB400。对单榀框架中的预应力筋组进行编号如图2所示。

图2 单榀框架结构(单位：mm)

根据工程实践，预应力损失的总和占张拉控制应力的15%～30%。所以在发生预应力损失30%的范围内，假定预应力筋组发生如表1所示的预应力损失，每跨梁均匀布置19个节点，从左到右依次布置，计算各节点的位移变化。各跨跨中的节点编号分别为10，29，48，67，由图3可得，发生预应力损失时，梁跨中位移变化最大，因此宜选取梁跨中位置作为主要位移监测点。

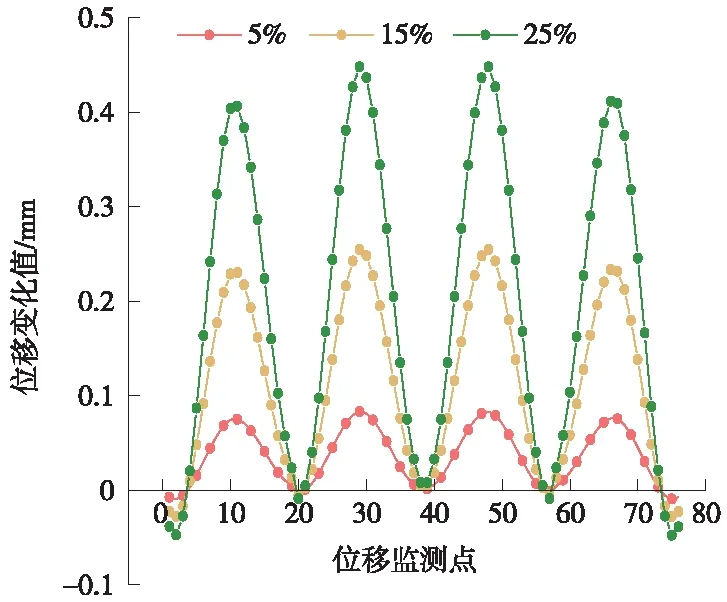
图3 不同工况下框架各节点位移变化

表1 预应力损失工况

2.2 单位预应力损失a%的选取原则

单位预应力损失量a%为预应力筋损失占初始张拉的百分比，是结构中预应力筋损失设定值。预应力框架结构在施工期间和竣工完成后，影响结构中预应力损失的因素较多，各因素对结构中预应力损失的影响大小难以确定。因此将单位预应力损失量作为结构预应力损失大小识别的“度量”，选择合适的单位预应力损失量能有效识别结构的预应力损失。

在框架结构中，主梁、次梁一般均布置预应力筋。主梁按有无次梁分为两类。本节选取如图4所示预应力框架结构，梁截面配筋如图5所示。钢筋和混凝土的材料参数与2.1节单榀框架的相同。

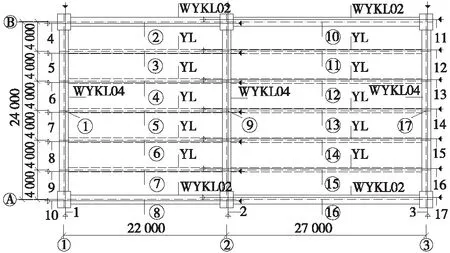
图4 框架平面、预应力筋组编号及观测点编号

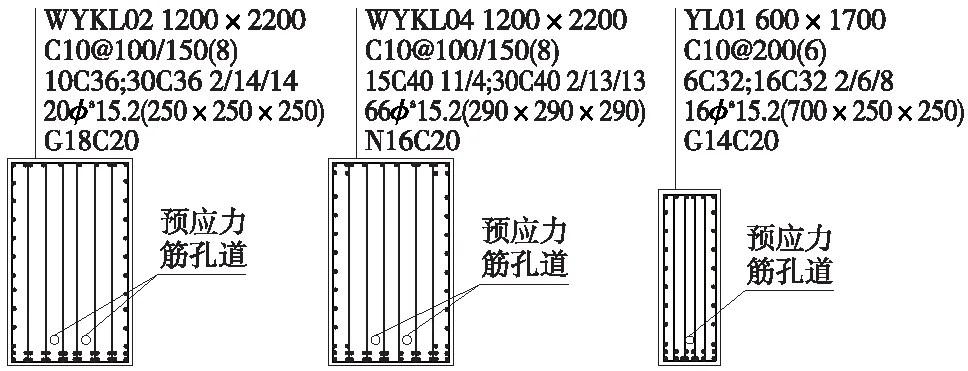
图5 梁截面配筋

将整体框架中的预应力筋组和位移监测点进行编号，如图4所示，预应力筋组编号1～17，监测点选在梁的跨中位置，编号①～。为研究单位预应力损失量a%的取值对影响矩阵识别精度的影响，计算单位预应力损失量分别为5%，15%，25%时的位移矩阵。当单位预应力损失量a%取15%时，参照2.1节的方法即可计算出结构的位移影响矩阵[C]。同理，当单位预应力损失量a%为5%，25%时，得到对应的位移影响矩阵。

[C]=

为研究由a%建立的位移影响矩阵对预应力损失识别结果精度的影响，假设图4中编号为2，3，12，13，14，15，16的预应力钢筋组实际发生如下预应力损失量，而其他组预应力钢筋未发生损失时，计算结构中位移监测点的位移变化值，形成位移变化矩阵。以下3组数据是在30%范围内随机抽取排列组成。

第一组：

[10% 6% 5% 8% 4% 3% 7%]；

第二组：

[12% 15% 14% 19% 18% 11% 13%]；

第三组：

[22% 28% 30% 20% 25% 26% 24%]。

在有限元模型中设定相应构件发生上述预应力损失，计算得出位移监测点的位移变化值作为实际位移变化值，得到实际位移列向量，记作：

M1=[0.160 0 -0.007 0.320 0.549 0.320 -0.007 0 0.917 0 0.450 1.238 1.184 0.752 0.645 0 0.685]T

M2=[0.209 0 0.004 0.416 0.689 0.418 0.005 0 1.168 0 1.329 2.697 3.176 1.888 1.229 0 1.627]T

M3=[0.397 0 0.013 0.791 1.304 0.792 0.014 0 2.211 -0.001 3.001 3.564 5.203 4.194 2.330 -0.001 3.181]T

将位移影响矩阵[C]和监测点位移变化列向量[M]代入公式(3)，利用MATLAB计算出预应力损失识别系数xj，根据公式(6)求出预应力损失量Pj。以实际损失量为横坐标，计算损失量除以实际损失量为纵坐标，将计算数据绘制坐标轴中如图6所示。

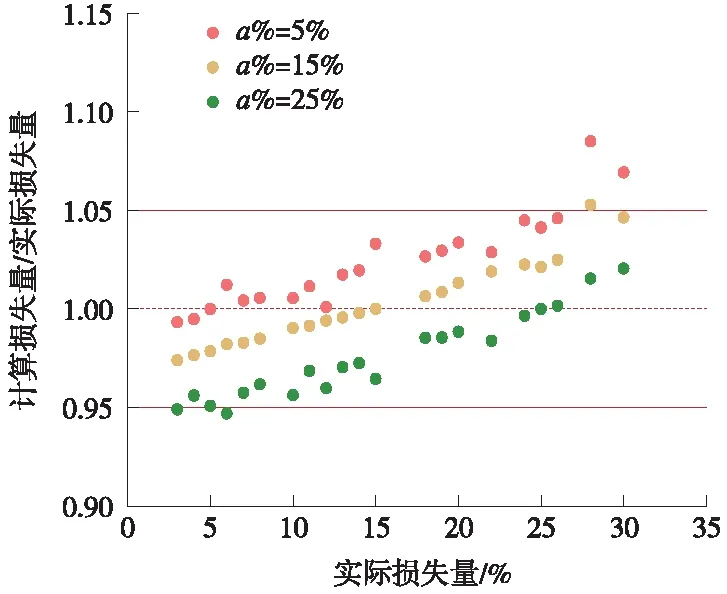
图6 识别数据图

从图6可知，选择的单位预应力损失量a%越接近构件的实际预应力损失量，计算出来的误差越小。当位移矩阵法计算得到的计算损失量与实际损失量比值在0.95～1.05，则认为计算值比较准确。用位于区间[0.95，1.05]内的点数与总点数的比值η来评价a%的准确性，η越大说明使用该a%计算得到的数据越准确。由图6可得：a%=5%时，η=19/21=90%；a%=15%时，η=20/21=95%；a%=25%时，η=20/21=95%。且a%=5%，误差均值0.543，误差方差0.462；a%=15%，误差均值0.218，误差方差0.225；a%=25%，误差均值-0.199，误差方差0.079。综上所述，用位移矩阵法能较精确地计算出预应力损失量，且当a%=25%时，计算得到的预应力损失量更加准确，误差较小，效果好。

3 结构发生预应力损失时梁的变形规律

为研究主梁、次梁分别发生预应力损失时对结构其余梁位移变化的影响规律。选取预应力混凝土框架结构，重新布置位移监测点如图7所示，预应力筋组编号同图4。设定表2工况。

图7 梁位移监测点布置示意

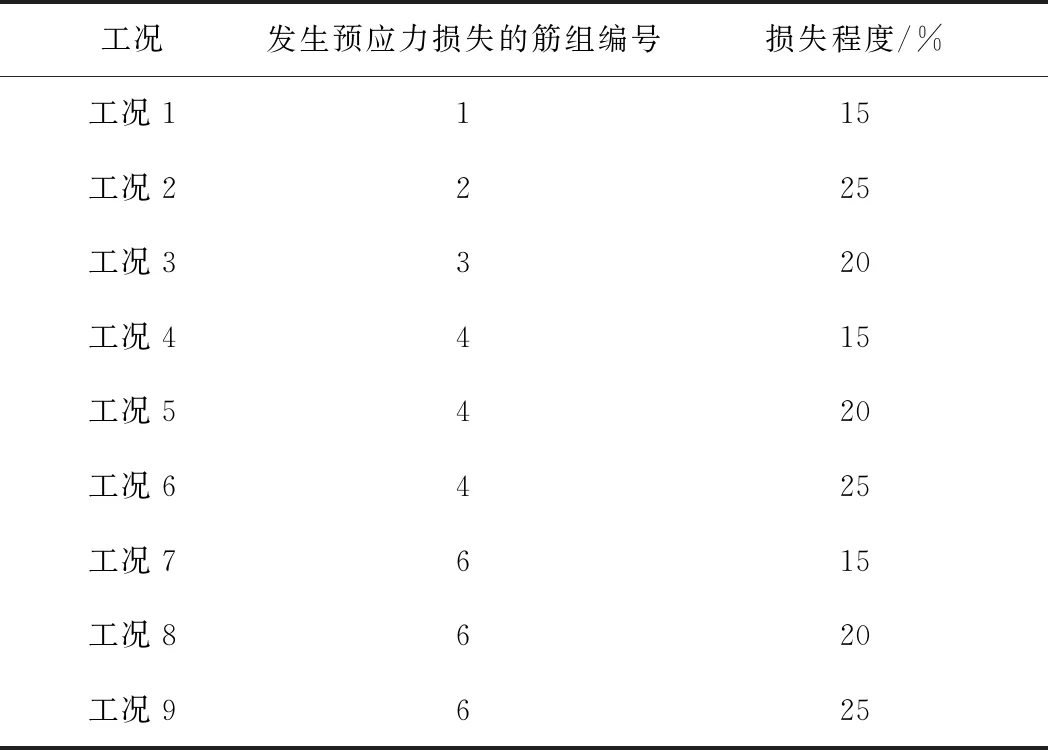
表2 预应力损失工况

各工况下结构位移监测点的位移变化值见图8～图10。

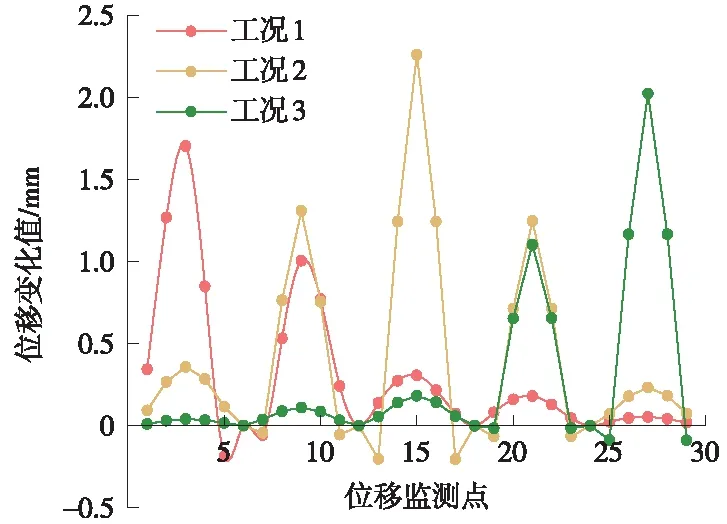
图8 工况1～工况3监测点位移变化曲线

如图8所示，预应力损失发生在主梁上，且该主梁有次梁连接。结果显示，有预应力损失的主梁位移变化最大，与之相连的次梁位移也发生变化，但与之相连的主梁位移不会发生变化。

如图9所示，预应力损失发生在主梁上，且该主梁没有次梁连接的情况下，只会引起该跨上观测点发生明显变化，其他跨内观测点的变化非常小。

图9 工况4～工况6监测点位移变化

由图10所示，仅次梁中发生预应力损失时，并未引起结构中主梁及相邻的次梁挠度值发生变化，只是引起了预应力筋所在位置的梁挠度变化。

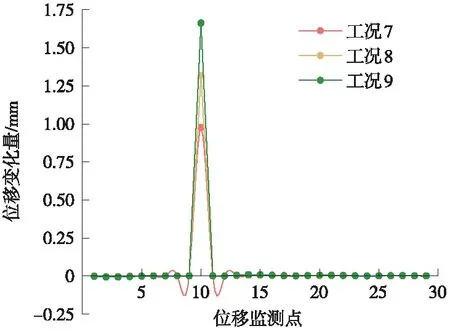
图10 工况7～工况9监测点位移变化曲线

以上主次梁的变形规律解释了位移影响矩阵中第4～第17列中每列只有一个元素不为0的现象。

4 结论

本文基于位移影响矩阵原理，提出了计算大跨预应力混凝土框架结构预应力筋预应力损失程度的方法。并且讨论了位移观测点的选取，分析单位预应力损失量a%对计算结果精度的影响。分析总结框架梁发生预应力损失时主次梁变形的规律。结论如下。

(1)本文提出的基于位移影响矩阵的预应力混凝土框架结构预应力损失计算方法可以用于该结构的预应力损失计算，计算精度较高。

(2)预应力梁发生预应力损失时，梁跨中位移变化最大，梁跨1/2处是最佳位移监测点。

(3)单位预应力损失量a%的取值对结构中预应力损失识别结果具有影响，当单位预应力损失量a%为25%时识别值误差较小，能比较准确地识别结构中发生的预应力损失，结果比较可靠。

(4)结构发生预应力损失时，若损失发生在有次梁连接的主梁上，有预应力损失的主梁和与之连接的次梁均产生位移变化，且该主梁的位移变化最大，但其他主梁位移不受影响；若损失发生在没有次梁连接的主梁上或者发生在次梁上时，只会对该梁本身位移有影响，对其他梁的位移没有影响。