基于瑞典条分法的铁路边坡极限状态设计研究
郭海强,王占盛,李安洪,徐 骏,谢清泉
(中铁二院工程集团有限责任公司,成都 610031)
引言
随着我国高铁“走出去”及“一带一路”倡议的实施,加速推进中国铁路标准与国际接轨的趋势迫在眉睫。铁路路基作为铁路工程重要的一环,必须提高其设计技术标准的科学性,适应国内外工程设计向极限状态设计方向发展的趋势,才能更好地与国际标准接轨[1]。在此过程中,为了配合铁路路基标准建立基于概率论的设计体系,各设计院及高校为路基相关规范的编制或修编开展了大量科研工作[2-10]。在以上科研工作的基础上,Q/CR9127—2018《铁路路基设计规范(极限状态法)》顺利颁布。
在参与修编Q/CR9127—2018《铁路路基设计规范(极限状态法)》过程中,发现在基于瑞典圆弧条分法的铁路边坡(路堤、路堑)稳定性极限状态设计表达式、分项系数及设计验证校准等方面仍需要进一步改善。为此,通过完善铁路路基边坡极限状态设计表达通式及不同设计速度下的路基边坡分项系数计算体系,来解决现行《铁路路基设计规范(极限状态法)》关于路基边坡设计所存在的问题。
1 总安全系数法与极限状态法对比
铁路路基边坡的总安全系数法与极限状态法对比如表1所示。铁路边坡(路堤、路堑)计算力系,如图1所示。

表1 总安全系数法与极限状态法对比[11-12]

图1 圆弧形滑面边坡条分计算示意
通过对比表1,可以发现关于路基边坡的极限状态设计表达式、分项系数及设计验证校准等方面需要进一步改善,具体如下。
1.1 设计表达式
铁路路堤及路堑边坡按照传统总安全系数法设计时,采用统一设计表达式,而按照极限状态法设计时却采用两种设计表达式,不便于使用。并且在路堤边坡的无荷检算时,路堤边坡表达式与路堑边坡相比表达式完全一致,但作用分项系数却不一致。
1.2 分项系数
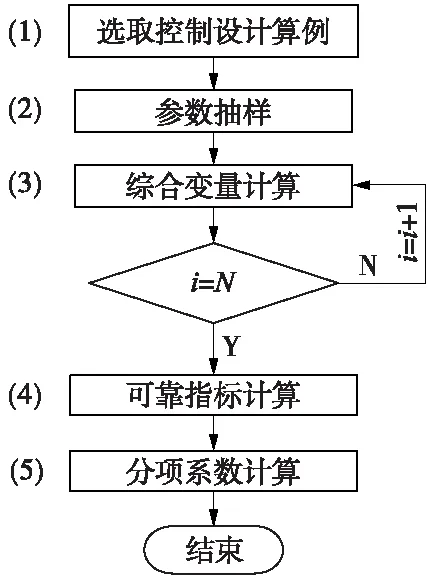
(1)Q/CR9127—2018《铁路路基设计规范(极限状态法)》提出的一般工况下路堤、路堑边坡的分项系数只按照速度250 km/h≤V≤350 km/h,K≥1.3,制定了分项系数,未考虑速度120 km/h (2)一般工况下路堤边坡的分项系数共有5项,分别为γ1,γ2,γ3,γ4,γ5,且均不小于1,若将总安全系数K≥1.3分解到这5项分项系数γi上,则平均每项分项系数γi≈1.05,若将K≥1.20均分,则平均每项分项系数γi≈1.04;若将地震工况下的边坡总安全系数K≥1.15按条文说明中给出的7项分项系数进行分解,则平均每项分项系数γi≈1.02。因此,是否有必要将分项系数分解如此之细,值得研究。 (3)铁路路堤边坡分项系数采用γ1,γ2,γ3,γ4,γ5进行表示,每项分项系数的定义不明确。 Q/CR9127—2018《铁路路基设计规范(极限状态法)》提出的一般工况下路堤、路堑边坡的极限状态设计分项系数,在银西、阳安、大张、哈佳及商合杭高速铁路的路基边坡工点进行了总安全系数法和极限状态法两种方法的试设计对比,发现两种设计方法的设计结果仍存在一定偏差,部分路堑边坡偏差较大。 综上,仍需对Q/CR9127—2018《铁路路基设计规范(极限状态法)》中所提出的一般工况下路堤、路堑边坡的极限状态设计表达式和分项系数体系做进一步理论研究。 为了得到铁路路堤及路堑边坡稳定性极限状态设计表达通式,并减少过多的分项系数,在充分参考Q/CR9127—2018《铁路路基设计规范(极限状态法)》的路堤与地基的整体稳定极限状态设计表达式及DL/T5395—2007《碾压式土石坝设计规范》中的土石坝稳定性极限状态设计表达式[12-13],将基于瑞典圆弧条分法的铁路路堤及路堑边坡稳定性极限状态设计表达通式修改为 (1) 式中γc——黏聚抗力分项系数; γf——摩擦抗力分项系数; γS——重力作用分项系数。 式(1)将边坡土条自重与主可变荷载统一合并,可从形式上将路基边坡及路堑边坡稳定性极限状态设计表达式统一,将分项系数缩减为3项,并且每项分项系数的定义均十分明确。若能够找到同时符合路堤及路堑边坡稳定性的极限状态分项系数,即可完全将铁路路堤及路堑边坡稳定性极限状态设计表达式及分项系数统一。 现有分项系数的计算方法主要包括以下4种。 (1)按分位值法确定理论设计值的方法。 (2)林德(Lind)的0.75线性分离法。 (3)幂级数展开法。 (4)一般分离法。 对于功能简单、可导的情况,可选择按分位值法确定理论设计值的方法确定分项系数,这种方法的分项系数对应于分项目标可靠指标,在概率论意义上的概念比较明确;反之则可在林德的0.75线性分离法、幂级数展开法及一般分离法3种方法中进行选择[14]。其中,当基本变量独立时,一般分离法为普遍适用的方法。Q/CR9127—2018《铁路路基设计规范(极限状态法)》中铁路路堤及路堑边坡分项系数即采用一般分离法获取[4,12]。 但是,当基本变量不独立时,采用一般分离法计算出的分项系数进行设计时会产生偏差,分项系数还需进一步校准。 团队通过研究,基于一般分离法建立了考虑相关性的分项系数计算方法,验证并得到了不同设计状况下的支挡结构极限状态设计分项系数建议值,相关成果已纳入Q/CR9127—2018《铁路路基设计规范(极限状态法)》中,并取得了理想的成果[2-3,6-7]。为此,将该方法进一步应用推广到铁路路基边坡的极限状态分项系数的制定,求取最优分项系数。 以路堑式边坡为例,采用蒙特卡洛法(Monte-Carlo)进行考虑相关性的边坡分项系数计算,计算流程如图2所示。 图2 分项系数计算流程 分项系数计算步骤如下。 (1)选取控制设计算例 在计算分项系数时,首先需选取控制设计的算例,如铁路设计速度为250 km/h≤V≤350 km/h时,选取一组边坡稳定安全系数接近的容许值(K≈1.3)的算例,进行分项系数计算。 采用边坡稳定性分析软件,进行大量工点试算,最终确定一组路堑边坡算例,计算过程从略。满足条件的路堑边坡岩土及边界条件如表2所示。 表2 路堑边坡岩土及边界条件 (2)参数抽样 对路堑边坡稳定性功能函数中的3个关键变量c、φ、γ进行随机抽样,随机变量统计特征如表3所示。 表3 随机变量统计特征[4,14] (3)综合变量计算 根据抽样次数,计算在各组参数组合下的3项综合变量(∑cili,∑Wicosθitanφi,∑Wisinθi)数值。 (4)可靠指标计算 统计各综合变量的统计特征,计算考虑相关性后的可靠指标,计算公式如式(2)所示[6] (2) 式中,μc为黏聚力抗力项均值;μc为摩擦抗力项均值;μS为作用项均值;σc+φ为总抗力标准差;ρc+φ,S为抗力与作用间的相关系数。 (5)计算分项系数 根据综合变量,计算考虑变量相关性后的分项系数,计算公式如式(3)所示[7] (3) 式中,βZ为可靠指标;δc,δφ,δS为综合变量变异系数;Φc,Φφ,ΦS为综合变量分离函数;ρS,c,ρφ,c,ρc,φ,ρS,φ,ρφ,S,ρS,c,ρc,S为各综合变量间的相关系数。 考虑变量相关性后的分项系数计算结果如表4所示。对比发现是否考虑变量相关性,对边坡稳定性的可靠指标及分项系数计算结果影响均较大。采用考虑变量相关性后得到的分项系数,进行极限状态设计与总安全系数法设计验证时,能够有效保证设计结果偏差控制在5%以内。 表4 路基边坡稳定性极限状态设计表达式中分项系数计算 (1)多组分项系数的计算 虽然前节考虑变量相关性后得到的分项系数较不考虑变量相关性的分项系数能够显著减小结果偏差,但是仍有优化空间。团队通过研究,进一步发现可靠指标与分项系数并非一一对应的关系,而是一对多的关系[15]。利用图3多组分项系数的计算程序,读取前节计算得到的3项综合变量文件R_C(∑cili),R_Fai(∑Wicosθitanφi),S_W(∑Wisinθi),可以获得多组满足要求的分项系数。 图3 多组分项系数计算程序界面 (2)寻找最优分项系数 通过以上方法可以得到多组分项系数,但又带来了新的问题,如何才能找到一组最优分项系数能够将路堤、路堑边坡稳定性极限状态设计分项系数统一且最大限度的消除偏差,保证铁路边坡极限状态法设计与总安全系数法设计一致。为此,通过引用单一安全系数法来寻找最优安全系数。 (4) 由式(4)可知,只有将关系式中的ρc消除,才能保证铁路边坡极限状态法设计与总安全系数法设计一致。否则,当确定极限状态分项系数(γc、γf、γS)后,设计验证结果仍会随着ρc的变化,产生一定的偏差。为消除ρc,需令γc=γf,则式(4)可进一步表示为 (5) 最终,在设计速度250 km/h≤V≤350 km/h下,通过在图3计算程序得到的多组分项系数中,选取γc=γf时的分项系数为最优极限状态分项系数。同理,按此方法可获取其他设计速度下的分项系数,结果如表5所示。 表5 不同设计速度下铁路路基边坡极限状态设计分项系数 为验证不同设计速度下,铁路路基边坡极限状态设计表达式及分项系数的合理性,对铁路路基边坡极限状态法进行充分的设计验证校准。 采用本文得到的铁路路基边坡稳定性极限状态设计表达式及分项系数,对大张、哈佳、商合杭高速铁路的试设计工点进行路堤、路堑边坡稳定性设计验证对比。两种方法均采用同一滑面,检算结果如表6所示。由表6可知,采用总安全系数法设计与极限状态法设计均满足稳定性要求。将总安全系数法安全系数除以[K0],得到总安全系数法的归一化值。对比总安全系数法归一化值与极限状态法抗力作用比值可以看出,路堤及路堑边坡稳定性的归一化差别不大,控制在2%以内。 表6 实际边坡稳定性设计结果对比 2.大张高速铁路时速200 km,[K0]=1.25;商合杭高速铁路时速350 km,[K0]=1.30;哈佳高速铁路时速250 km,[K0]=1.30。 由于实际工点的样本量偏少,不能充分校准不同设计速度下的边坡极限状态分项系数。为此,对不同设计速度下的126组铁路路基边坡进行全面的设计验证校准,计算结果偏差如表7所示。由表7可知,采用本文推荐的路基边坡极限状态设计表达式及分项系数,能够很好地消除设计中存在的偏差,并且将最大偏差降到2%以内。 表7 不同设计速度下铁路路基边坡稳定性设计结果对比 此外,需要说明的是,设计结果仍然存在偏差是由于选取分项系数时,对分项系数进行取整造成的;若不对分项系数取整,则可完全消除偏差,与总安全系数法一致。 通过对基于瑞典圆弧条分法的铁路路基边坡极限状态设计方法研究,可以得到以下主要结论。 (1)提出了一般工况下,基于瑞典圆弧法的铁路路堤、路堑边坡的极限状态设计表达通式 (2)提出了一般工况下,不同设计速度下的分项系数:当250 km/h≤V≤350 km/h时,γc=1.15,γφ=1.15,γS=1.15;当120 km/h (3)给出了考虑相关性的铁路路基边坡极限状态设计的分项系数计算方法及步骤。 (4)完善了一般工况下铁路路基边坡的极限状态设计表达式和分项系数计算体系,解决了现行《铁路路基设计规范(极限状态法)》关于路基边坡设计所存在的问题。1.3 设计验证校准
2 铁路路基边坡极限状态设计表达通式

3 分项系数的确定
3.1 现有分项系数计算方法
3.2 考虑相关性的边坡分项系数计算



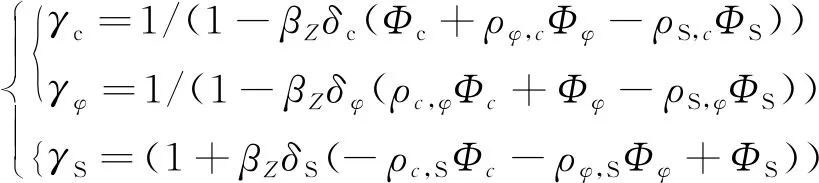

3.3 寻找最优分项系数




4 设计验证校准
4.1 实际边坡工点设计验证校准

4.2 全面设计验证校准

5 结论

