基于代理模型的三立柱半潜平台多目标优化

丘文桢，宋兴宇，张新曙

(上海交通大学 海洋工程国家重点实验室;高新船舶与深海开发装备协同创新中心，上海 200240)

在半潜型平台(SEMI)初始设计阶段，平台主尺度是影响平台水动力性能和建造成本的关键性因素.因此，对半潜平台的水动力特性进行数值预报及对其船体主尺度进行多目标优化是一项极具工程意义的研究工作.半潜平台在极限波浪下的大幅度运动和气隙等问题是平台研发中需要全面考虑的重要部分[1].

2006年，陈新权等[2]以半潜平台的钢材重量为优化目标，对超深水半潜式平台进行单目标优化.2015年，Park等[3]对半潜平台进行了水动力性能计算分析，以平台总重量和垂荡运动作为两个目标进行优化.优化过程通过分配不同的权值将多目标问题转换为单目标问题来求解，最终获得Pareto解集.2016 年，Kim等[4]采用模拟退火法对张力腿(TLP)平台进行多目标全局优化，两个优化目标分别为垂荡运动和平台重量，通过分配目标函数不同的权值来获得最终Pareto解集，优化过程中考虑了张力腿的强度极限和疲劳极限.2017年，Zhang等[5]对传统半潜型平台的多个主尺度参数进行了单参数敏感性分析，发现当平台吃水增加时，平台垂荡运动减小，并且当立柱宽度、浮箱宽度或浮箱高度减小时，平台垂荡运动运动也将减小.2017年，周佳等[6]采用试验设计的方法选取样本点，计算了这些样本点对应不同主尺度半潜平台的水动力性能，以垂荡运动响应作为目标，同时以气隙、稳性、排水量作为约束进行优化设计.2018年，Zhang等[7]选择一座TLP平台主尺度中的吃水、立柱间距、立柱直径及浮箱尺寸作为设计变量，采用非支配排序遗传算法对该TLP平台进行多目标优化，相较TLP平台初始设计，最终得到的优化方案在张力腿最大动态张力和平台总重量两方面性能上得到优化.

目前，设计者主要依据工程经验以及已建造完成的平台资料确定合适的浮体主尺度，不仅耗费大量人力和时间成本，而且容易陷入局部最优的误区，难以达到最优的平台主尺度.因此，本文提出一种新的方法，将代理模型引入优化过程中，将复杂耗时的数值模拟用建立起的代理模型替代，使得优化过程中的每次数值模拟的计算与分析变成简单的函数寻优，优化时间大大减小，优化效率显著提升.

1 多目标优化理论基础

本文以三立柱半潜平台为研究案例，以垂荡运动性能和平台总重量作为两个优化目标，采用粒子群优化研究三立柱半潜平台的优化方案，优化过程中为了提升优化效率建立了径向基函数代理模型，最终得到半潜平台的优化策略，优化整体流程如图1所示.首先，通过全析因方法得到平台样本点，并对样本点对应的半潜平台形式进行数值仿真计算.同时对平台附近的波面升高进行监测，计算平台气隙值.然后，根据数据库建立基于径向基函数的代理模型，通过缺一交叉验证法得到径向基函数中的形参数值，构成完整的代理模型.最后，采用粒子群优化算法，对半潜平台进行多目标优化.

图1 半潜型平台优化整体流程Fig.1 Flowchart of overall optimization process for SEMI

1.1 代理模型的建立

代理模型可以将复杂数值仿真中特定输入与输出的真实映射关系用简单的函数映射关系来替代[8].可用于求解计算量较大的各个领域.通过试验设计法选择合适的样本点，通过样本点(输入)计算原模型的响应(输出)，建立简单的数学关系，将数值模拟的过程用简单的函数计算来代替，计算量很小，能够快速地评估特定的设计方案.因此，本文建立代理模型的函数映射关系来替代数值仿真的真实映射关系，并将代理模型用于之后的半潜平台多目标粒子群优化.代理模型采用缺一交叉验证法对其精度进行交叉验证.

1.2 全析因试验设计法

在有限的试验条件下尽可能减少试验次数，同时尽可能多的获取样本数据信息，需要合适的试验设计策略.在试验设计领域中，主要有两个衡量维度：①因素，指的是试验的设计变量.②因素中的水平，即设计变量的多个变化梯度，两者共同作用对试验结果产生影响[9].因此，这两个维度是设计试验时所需控制与改变的.在半潜平台优化过程问题中，主尺度对平台的水动力性能影响较大，因此将半潜平台立柱与浮箱的几个几何参数作为试验设计的因素，将几何参数设置3～5个梯度，作为因素内的水平.明确了试验设计中两个维度，就可以选取试验样本点.考虑到半潜平台在试验设计中的因素数和水平数，采用全析因试验设计方案所消耗的时间在 1～2天内，是满足构建数据库可行性的时间长度，因此决定采用全析因试验设计.

1.3 径向基函数模型

径向基函数(RBF)具有学习速度快、拟合能力强及形式结构简单的优点，其形参数较少，使得确定形参数过程变得极为方便，并且具有较好的数值稳定性[10].径向基函数法不仅可以处理线性问题而且在非线性问题时，也可获得较高的预测精度，因此在工程中的应用范围非常广.由于径向基函数法方法在处理多变量及非线性问题时突出的优势，本研究也采用径向基函数的方法来构造代理模型.目前，径向基函数构建的代理模型主要分成输入层、隐含层及输出层，如图2所示.输入层xj(j=1,2,…,Q)为第j个样本点的设计变量向量，隐含层gj(j=1,2,…,Q)为第j个样本点对应的径向基函数向量，wj(j=1,2,…,Q)为第j个样本点对应的权值向量，输出层yj(j=1,2,…,Q)为第j个样本点的目标函数向量，Q为数据库中样本点个数.通过计算样本点与预测点之间的欧氏距离r=‖Δx‖(Δx为样本点与预测点之间的向量)，可以将输入的多个变量从多维度空间距离转化为一维距离.输出层是由隐含层中带有权值的径向基函数线性相加得到.

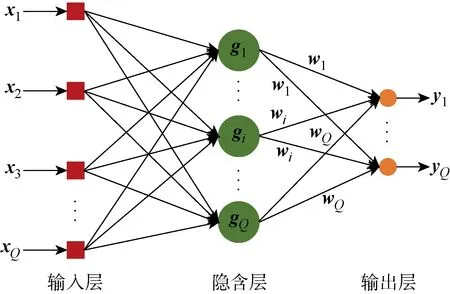
图2 径向基函数原理图Fig.2 Schematic diagram of RBF

基于径向基函数的代理模型建立流程如下：

假设样本点的输入矩阵为X，X及其相对应的输出矩阵Y分别为

(1)

式中：xij为第j个样本点的设计变量xj=[x1jx2j…xMj]T的第i个变量值；yij为第j个样本点的目标函数yj=[y1jy2j…yNj]T的第i个目标值；M为设计变量的维度；N为目标值的维度.

径向基函数可表示为

(2)

j=1,2,…,Q

式中：x=[x1x2…xM]T为插值点的向量；b为形参数.

径向基函数中的形参数b可以通过缺一交叉验证法求得一个最优值，该值使得基于径向基函数的代理模型的预测精度最高.确定b后，通过径向基函数将输入层转到隐含层，构成隐含层矩阵G:

(3)

得到隐含层与输出层之间的权值矩阵：

(4)

即可完成RBF模型的建立：

Y=WG

(5)

1.4 缺一交叉验证法

在构造径向基函数时，需要确定其中的形参数，它对整个代理模型的拟合精度有着十分重要的影响.因此，需要找到合适的形参数，使得代理模型精度达到最高，具体流程如图3所示.

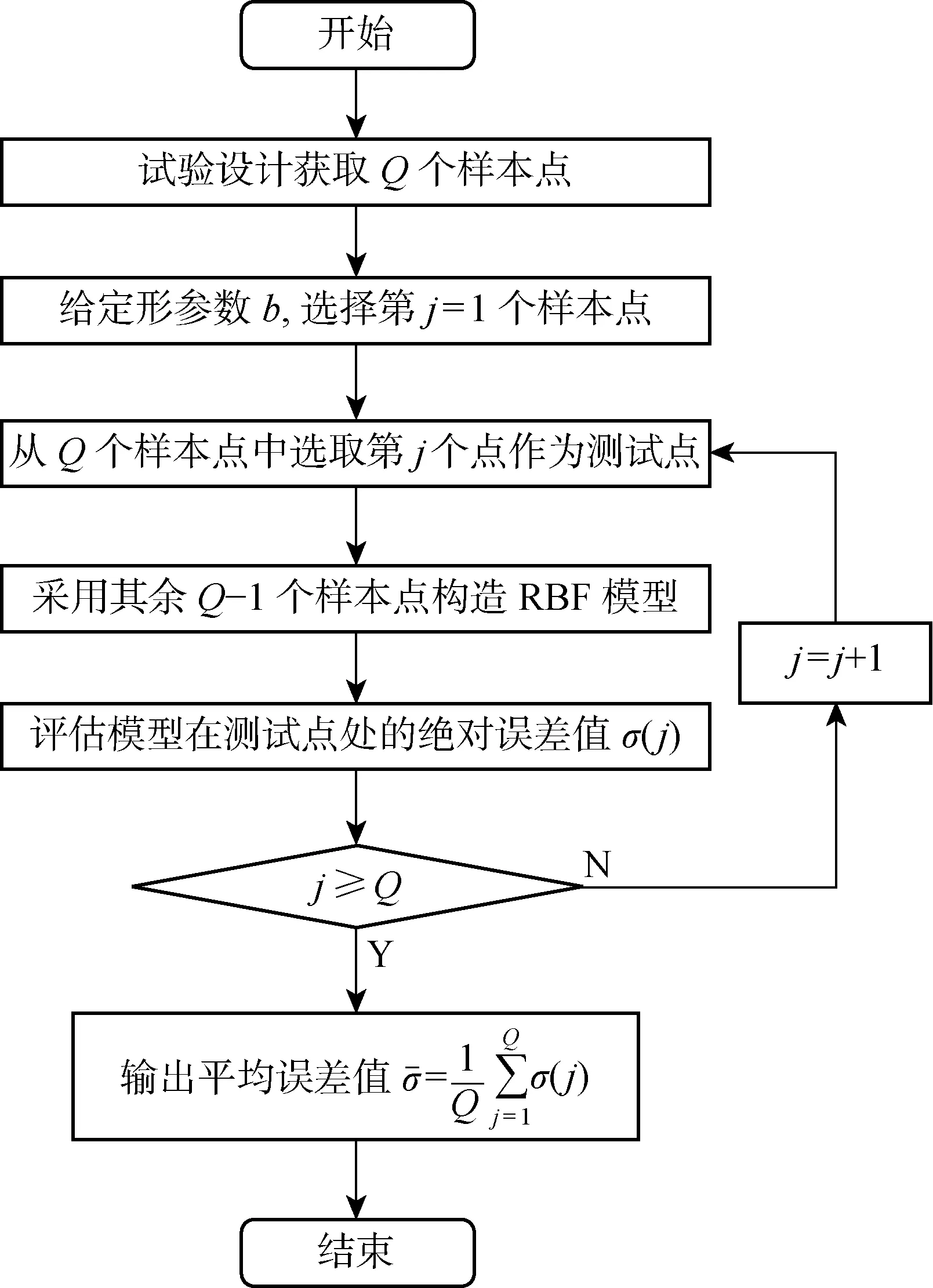
图3 缺一交叉验证法流程图Fig.3 Flowchart of leave-one-out cross validation

通过图中过程可以得到不同形参数与代理模型预测精度之间的关系，并绘制不同形参数与代理模型预测精度之间曲线，找到误差最小情况下的点，该点对应的形参数即为最佳形参数.

2 多目标优化算法的应用

海洋平台设计过程中，通常希望尽可能提高平台质量，又希望可以降低成本，而安全性和经济性往往就是两个矛盾的目标，因此需要在这两个矛盾的目标中找准平衡点，得到优化的设计方案.本文提出一种新的方法，将代理模型引入优化过程中，将复杂耗时的数值模拟用建立起的代理模型替代，使得优化过程中的每次数值模拟的计算与分析变成简单的函数寻优，优化时间大大减小，优化效率显著提升.

本研究采用粒子群优化算法，其主要思想建立在团队与个体间的协作和信息共享之上[11].粒子群优化算法整体流程如图4所示，粒子间通过个体与小团体间的信息共享找到当前小群体内的最佳位置，并和其他小群体进行进一步的比较分析找到全局最佳位置，由此决定粒子下一步的移动方向[12].

图4 粒子群优化算法流程图Fig.4 Flowchart of particle swarm optimization algorithm

Reyes-Sierra等[13]提出了多目标粒子群优化算法(MOPSO)，其原理基于粒子群算法，都是通过粒子间共享信息得到个体历史最优和全局历史最优，进而在个体历史最优和全局历史最优的共同作用下，向下一个方向寻优.但是，多目标粒子群算法与单目标粒子群算法所不同的是存在多个局部或全局最佳粒子的标准，因此多目标粒子群优化中引入了非支配排序和粒子间拥挤距离的概念[14].非支配排序指的是多目标方案的优劣，通过方案间的支配关系来确定，是多目标问题中的排序方法，而拥挤距离是同等级支配关系中的排序依据，指的是粒子与其同优先等级所有粒子之间的欧氏距离，如果拥挤距离较小说明Pareto前沿的粒子之间分布存在过于密集区域，是研究过程中需要避免的.根据以上两个法则，优化过程中可以对所有个体进行排序，多目标粒子群算法可不断更新最优位置，进行不断地迭代寻求最优解集.

3 半潜型平台的多目标优化

采用美国Principle Power的WindFloat基础平台为基础模型，WindFloat平台主要针对5 MW风力机，由3个大型浮筒和若干个斜杆组成，3个浮筒垂直竖起呈三角形分布，浮筒间由斜杆连接.三立柱半潜型平台如图5所示，初始设计半潜型平台主尺度如表1所示.图中及表中：D为吃水，FB 为干舷，CD、CS分别为立柱直径和立柱间距，垂荡板边长为HPL，排水量为Δ.根据给出的半潜型平台主尺度建立面元模型与Morison模型，由于三立柱半潜平台存在一个对称面，因此在建立面元模型时可以仅对平台的二分之一进行建模，如图6所示，可以减少面元数量，节省计算时间，为后续大量样本计算提供便利.

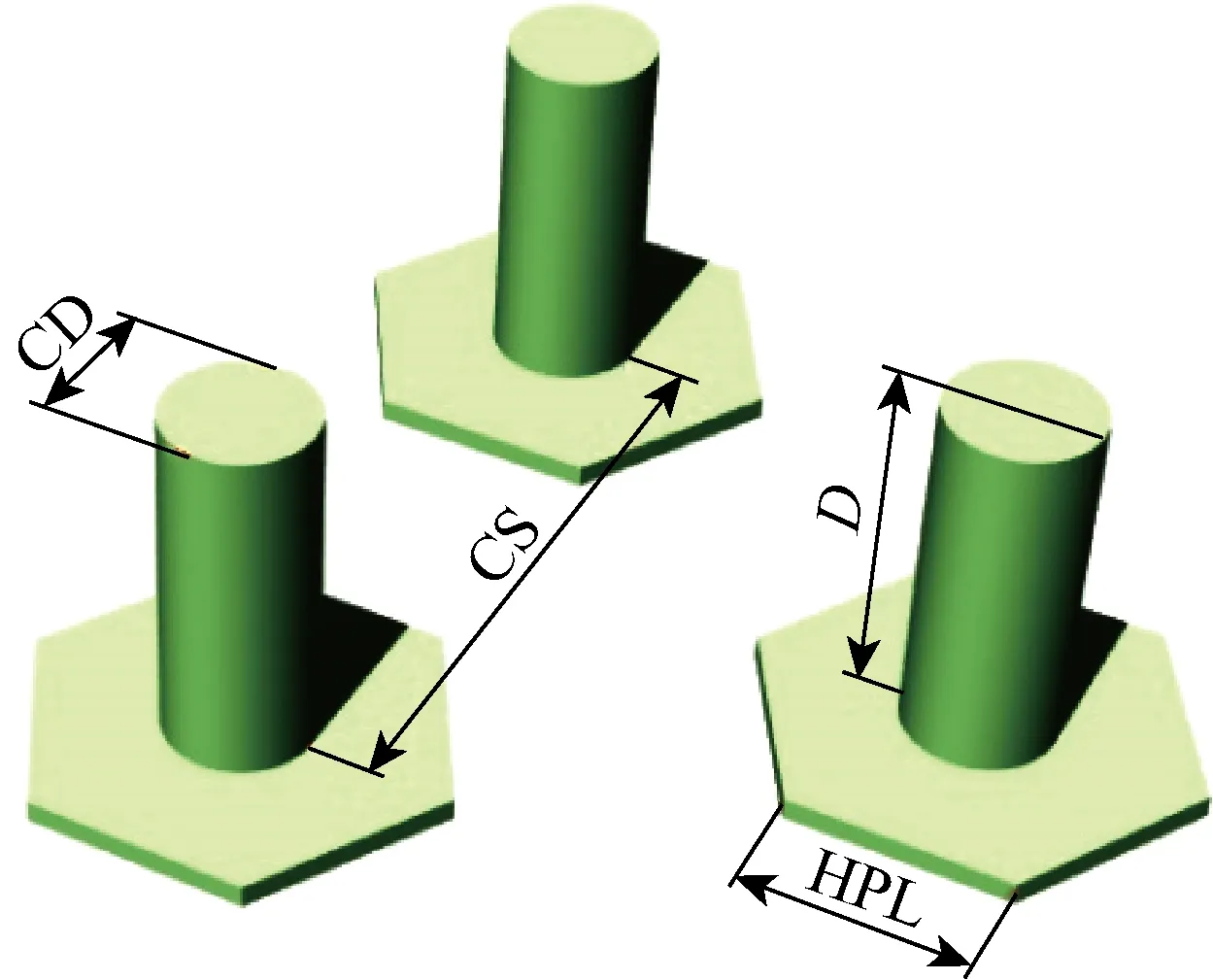
图5 三立柱半潜型平台示意图Fig.5 Sketch of three-column SEMI

表1 初始半潜型平台的主尺度Tab.1 Main particulars of initial SEMI

图6 面元模型Fig.6 Panel model

3.1 平台气隙计算

气隙是平台下甲板下边缘到波浪表面的垂直距离，为了防止波浪对甲板及甲板上设备产生抨击，保证平台在恶劣海况中有足够的气隙十分重要.为预报平台周围自由液面的波面升高情况与最小气隙的发生位置，需要科学合理地布置监测点，考虑到计算效率的问题，适当减少了气隙监测点的布置，具体气隙监测点布置如图7所示.

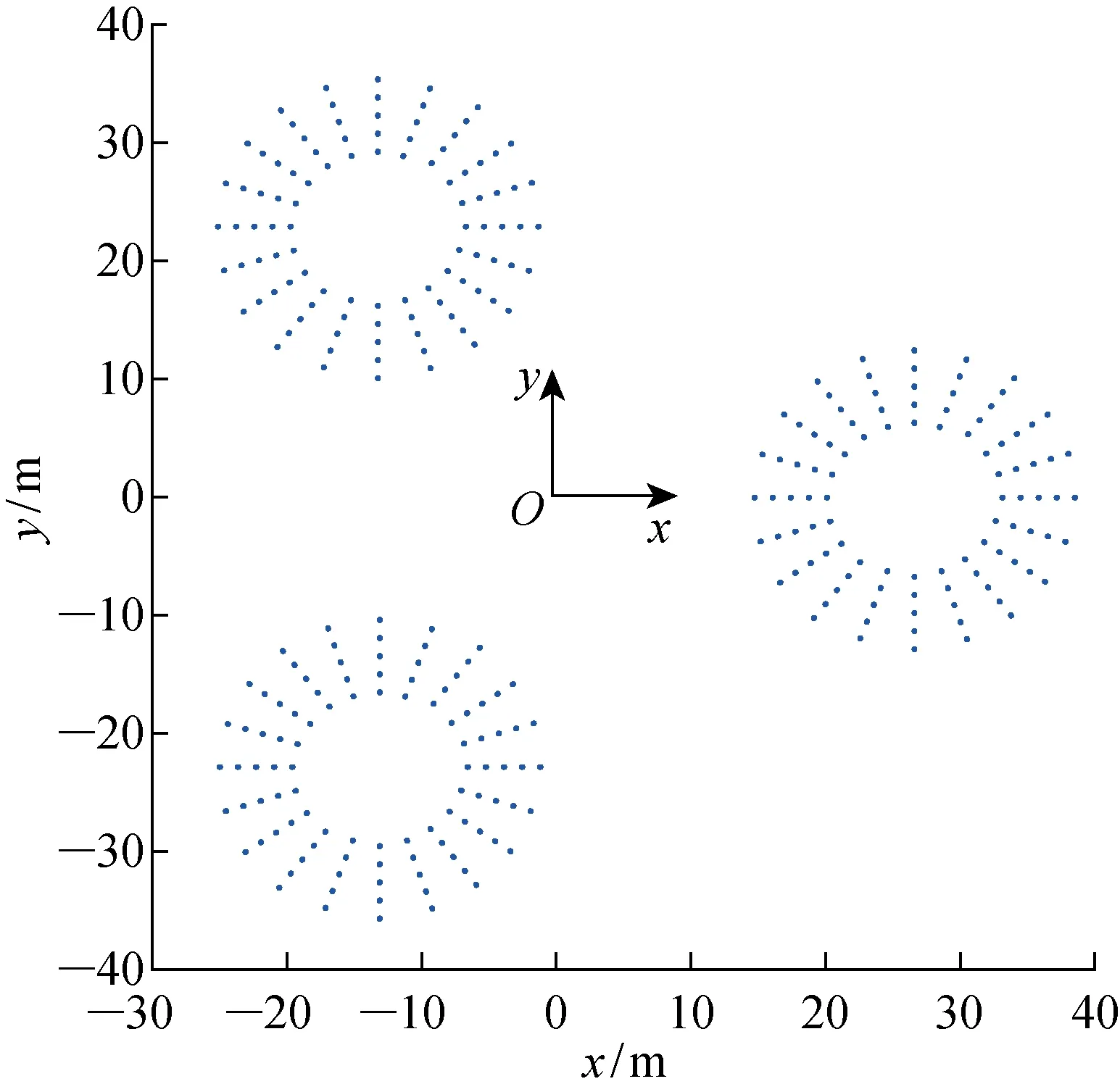
图7 半潜型平台气隙监测点布置图Fig.7 Layout of probes for estimating airgap of SEMI

本研究参考美国石油协会(API)发布的有关墨西哥海域海况风浪谱的2MET文件，本半潜平台的生存海况设定为墨西哥湾百年一遇海况，其主要参数如表2所示.表中：Hs为有义波高，Tp为谱峰周期，γ为谱峰升高因子，σa和σb为峰形参数，t为海况持续时间，f(θ)为方向谱.

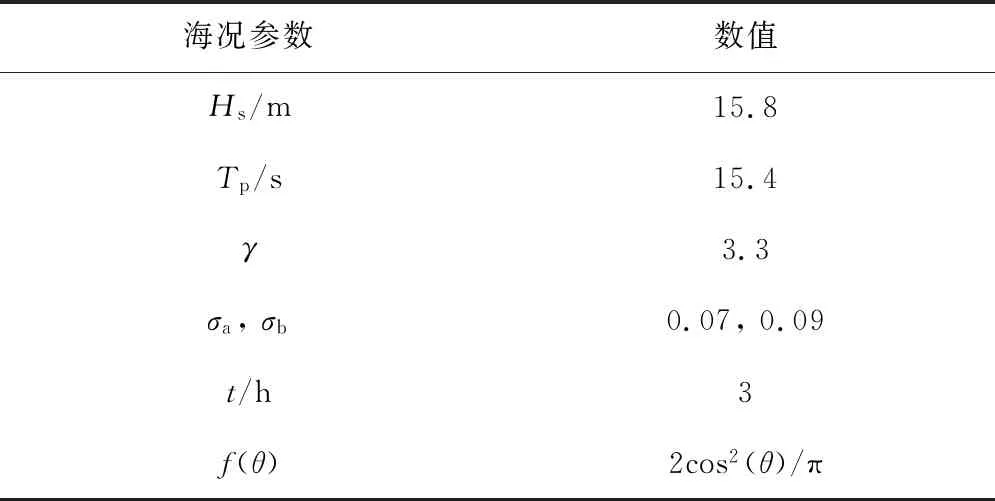
表2 墨西哥湾百年一遇海况(JONSWAP风浪谱)Tab.2 Sea condition of a-hundred-year recurrence period in Gulf of Mexico (JONSWAP wind wave spectrum)

考虑平台运动与波面升高的耦合影响，在绝对波面升高计算结果的基础上，将平台的垂向运动进行耦合，包括横摇、纵摇和垂荡运动，计算每个监测点的相对波面升高.随后用平台的静态气隙减去相对波面升高即为平台的气隙，平台极限气隙云图如图8所示.图中：AG为气隙，Col1、Col2及Col3为3个立柱.

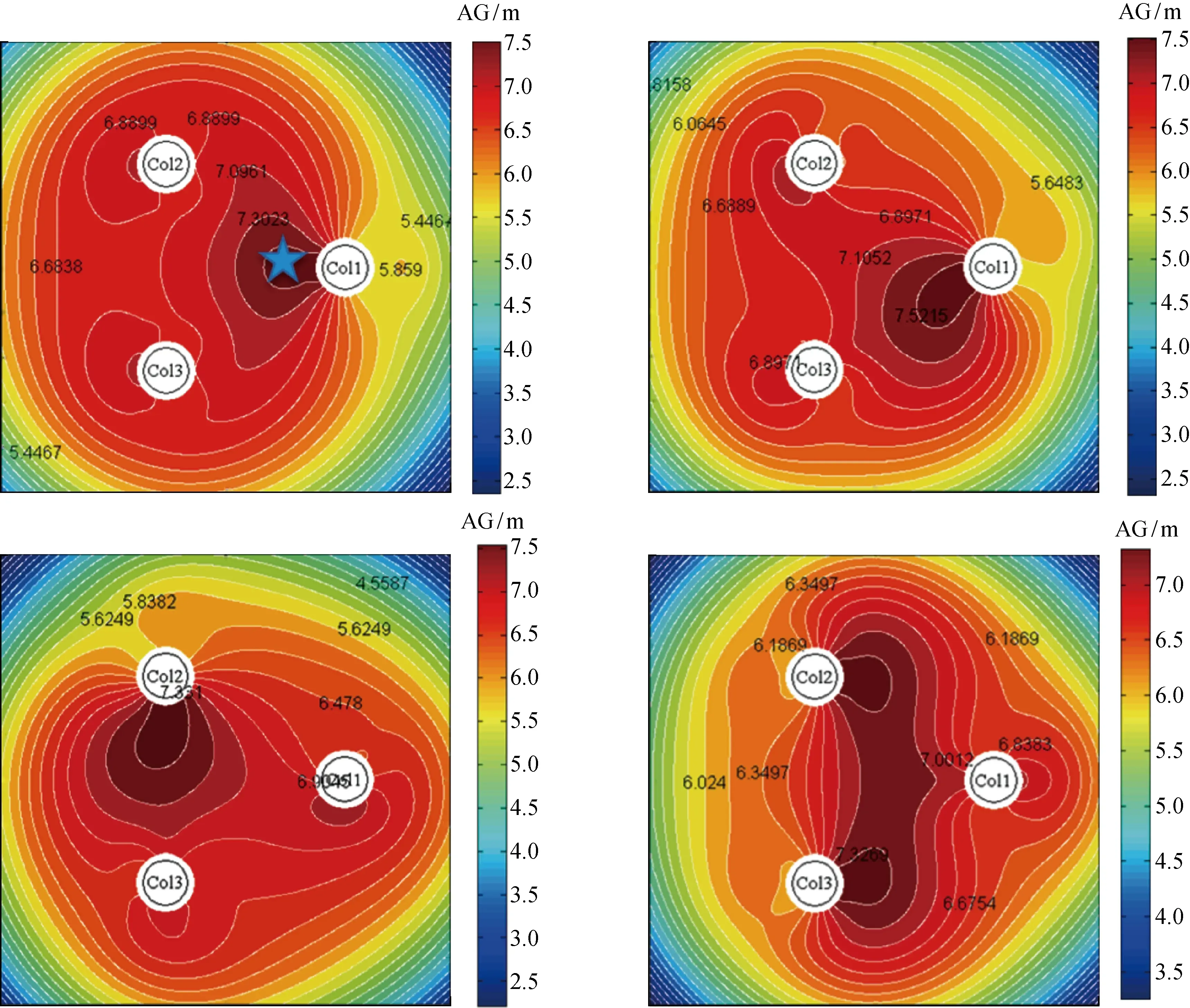
图8 半潜型平台在生存海况下气隙云图Fig.8 Airgap contour of SEMI in survival conditions

3.2 建立代理模型

本研究采用全析因设计法，选取吃水、立柱直径、立柱间距和垂荡板边长作为设计变量，其中吃水和垂荡板边长设置5层梯度，立柱直径和立柱间距设置3层梯度，根据排列组合原理得到共5×5×3×3=225个样本点，具体数值如表3所示.建立每个样本点所代表的模型，进行数值模拟计算得到每个样本点的目标值和约束值，包括最大垂荡运动响应X3,max、最大纵荡运动响应X1,max、最小气隙值AGmin、稳性高度GM和平台重量Wt，计算完所有样本点后，将所有样本数据保存，构建样本数据库.

表3 半潜型平台的全析因试验设计主要参数Tab.3 Main parameters of full factorial design for SEMI

得到样本数据库后，可以通过径向基函数构造代理模型，在构造径向基函数时，需要确定其中的形参数，它对整个代理模型的拟合精度有着十分重要的影响.本研究构建了预测最大垂荡运动响应、预测最大纵荡运动响应、预测平台最小气隙和平台稳性的代理模型.代理模型通过缺一交叉验证法去寻找最优形参数值，可以得到不同形参数与代理模型预测精度之间的关系，将最优形参数代入，进一步验证预测结果.如图9所示，横轴为各样本的数值模拟结果，纵轴为各样本的代理模型预测结果，两者基本一致，验证了最佳形参数下代理模型的预测精度.确定好最佳形参数后，即可构建完整的代理模型.

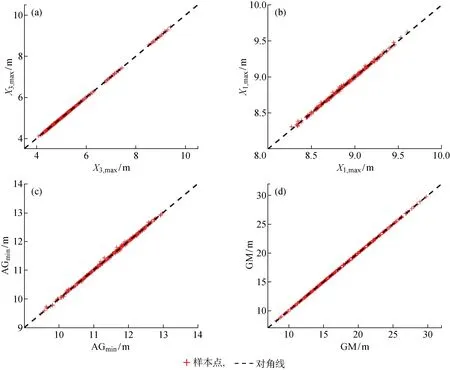
图9 缺一交叉验证法Fig.9 Leave-one-out cross validation method

3.3 单参数敏感性分析

代理模型预测速度快，可进行单参数敏感性分析.最大垂荡运动对半潜平台影响最大，故研究平台垂荡运动对主尺度的敏感性，如图10所示.

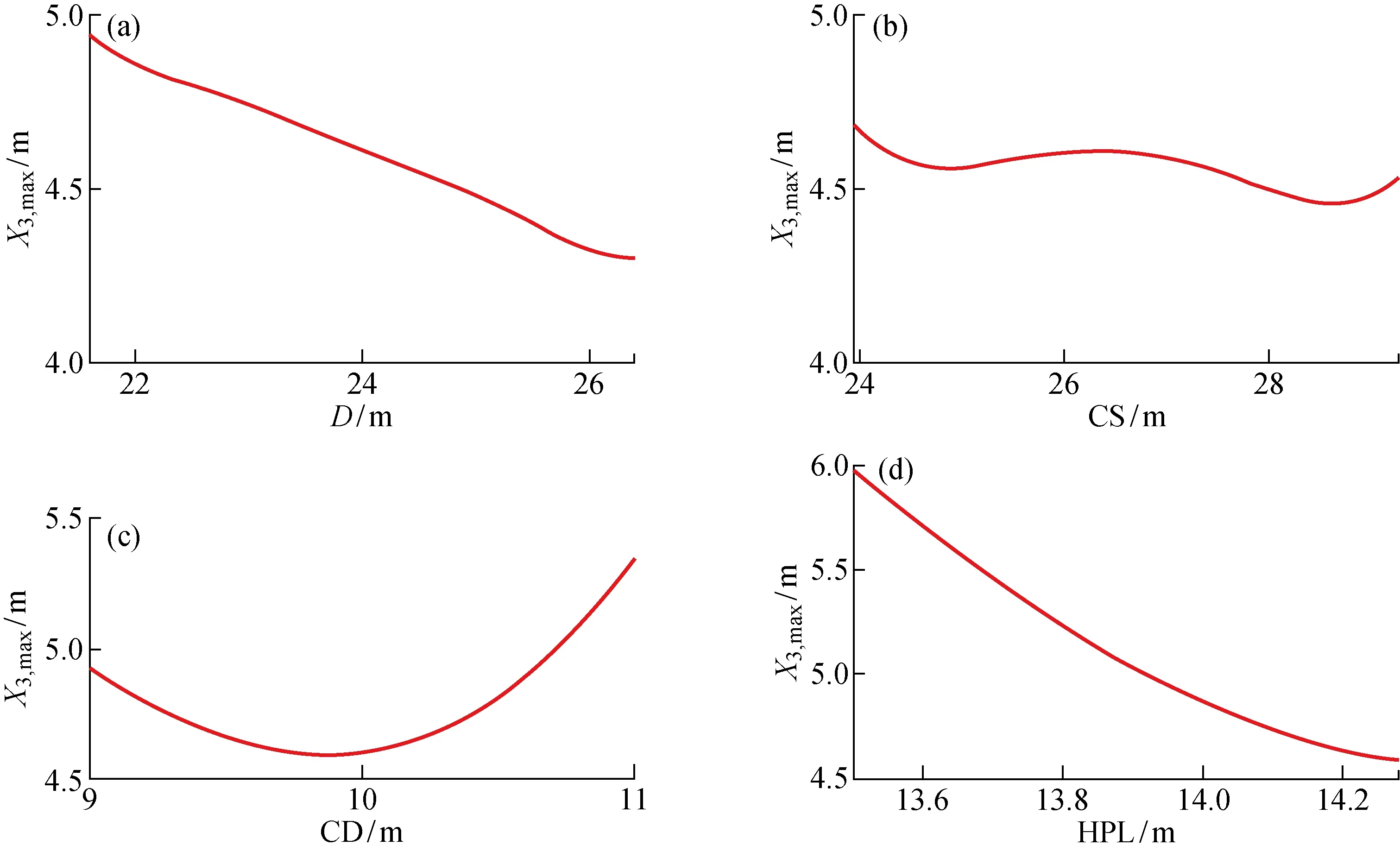
图10 半潜平台主尺度与最大垂荡运动响应关系Fig.10 Correlations between main particulars of SEMI and maximum heave motion response

可以发现，当吃水增加或者垂荡板边长增加而其他变量不变时，最大垂荡运动响应逐渐减小.比较几个参数变化对垂荡运动改变的影响大小，可以发现立柱间距改变对垂荡运动变化影响较小.

3.4 多目标粒子群优化

本研究采用多目标粒子群算法进行半潜平台的优化，将上面建好的代理模型用于多目标粒子群优化的过程中，实现快速智能和自动化寻优.优化区域限定在各个变量的初始值的上下10%区域内.优化过程中，目标函数为：① minX3,max；② minWt.平台需要满足的3个约束条件为：①X1,max<9 m；② AGmin>3.5 m；③ GM>3 m.

通过编写多目标粒子群优化算法，进行半潜平台主尺度寻优，最后获得30个Pareto最优解集.每个解对应一种平台主尺度，因而可以得到30种优化方案，其结果如表4所示.

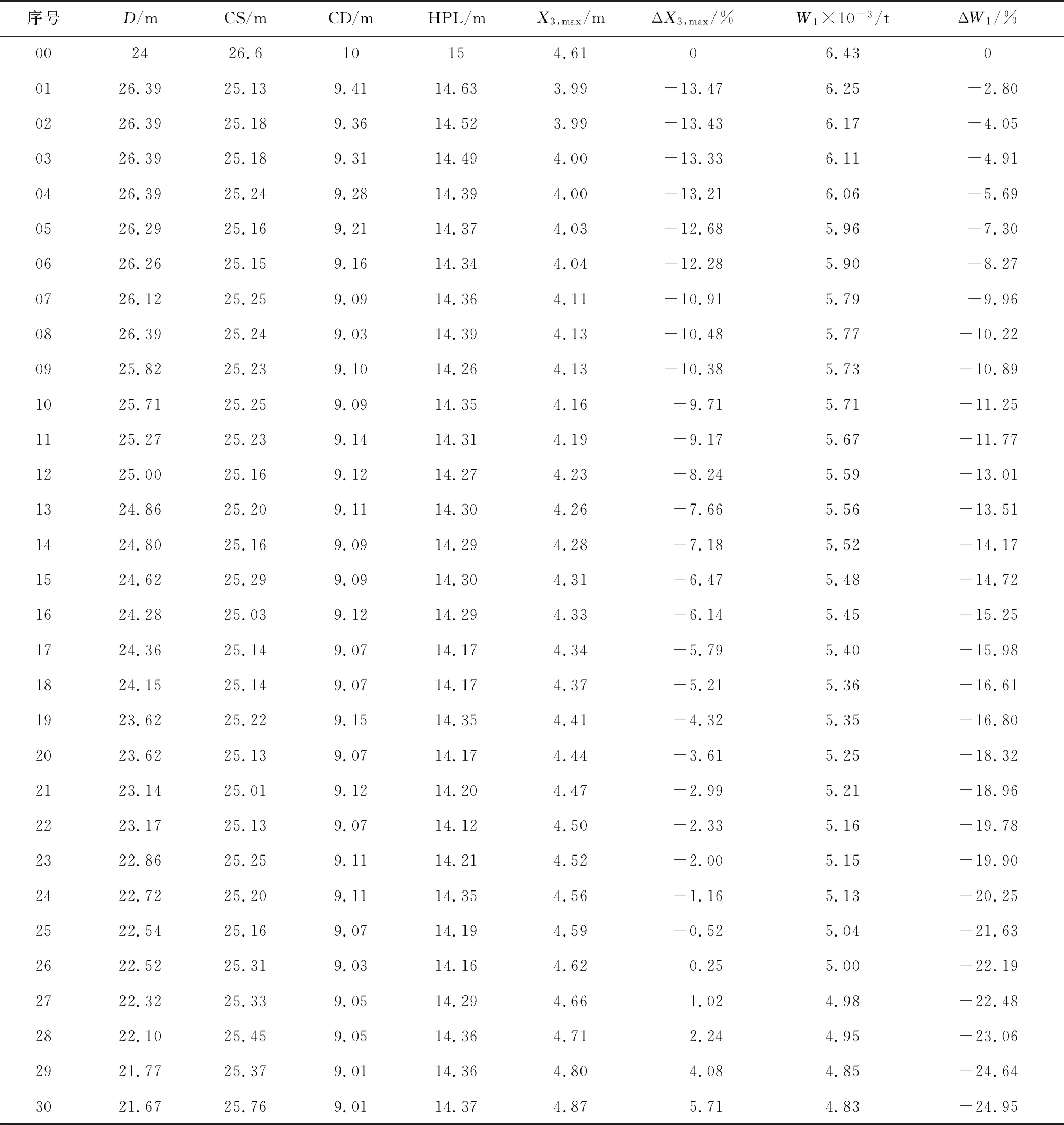
表4 半潜平台多目标粒子群优化Pareto最优解Tab.4 The Pareto-optimal solutions for SEMI obtained by utilizing MOPSO

表中00号为初始设计方案的主尺度，1～30号垂荡运动响应依次上升，总重量依次下降.通过将优化方案和初始方案比较可知，垂荡运动减小最大方案为1号平台主尺度方案，较初始方案减小了13.47%，总重量减小了2.8%.此外，将最大垂荡运动作为横坐标，平台总重量作为纵坐标，绘制30个优化方案和试验设计中建立的样本点于同一幅图中，如图11所示，图中的菱形符号代表初始平台设计的两个目标值，通过这个点的垂直轴和水平轴，将图分成4个区域.如果图中存在点位于左下角的区域，则表示该点代表的设计方案在垂荡运动响应和总重量这两个目标上均比优化之前有所改善，该点设计方案对初始设计是支配关系.在本研究中，位于左下区域的25个Pareto最优解方案在两个目标方面都优于初始设计.另外5个Pareto最优解位于右下区域，对应于表中26～30号设计方案，虽然此方案在最大垂荡运动响应方面较初始设计略差，但在总重量方面相对初始设计提升很大，因而较初始设计也是优化方案.

图11 半潜型平台Pareto最优解Fig.11 Pareto-optimal solutions for SEMI

为了进一步验证代理模型计算所得到的结果准确性，将30个设计方案用SESAM软件进行数值模拟再一次计算，得到30个方案的数值模拟结果，进一步通过下式求代理模型与数值模拟的相对误差百分数：

(6)

式中：X3,s为代理模型计算所得垂荡运动响应值，X3,d为直接数值模拟计算所得垂荡运动响应值.此外，由于平台的总重量是通过平台主尺度进行估计，并非通过代理模型预测，所以在总重量方面不存在误差，以Pareto解集的序号为横坐标，以代理模型与数值模拟的相对误差百分数为纵坐标，将计算结果绘制成图12，发现最大相对误差小于2%，这进一步证实了本代理模型的准确性.

图12 代理模型与数值模拟结果的相对误差Fig.12 Relative error between results of surrogate model and numerical simulation

4 结语

在三立柱风机半潜型平台初始设计阶段，平台主尺度是影响平台水动力性能和建造成本的关键性因素.因此，对半潜型平台的水动力特性进行数值预报及对其船体主尺度进行多目标优化是一项极具工程意义的研究工作.本文提出一种基于代理模型实现多目标快速优化的设计方法，以半潜平台安全性和经济性作为两个优化目标，以平台稳性、气隙高度及水平方向运动性能作为约束条件，采用多目标粒子群优化算法研究半潜平台的优化方案，优化过程中为了提升优化效率建立了径向基函数代理模型.最终得到半潜平台的30个优化方案，并开发出一套完整的平台优化设计程序.

基于代理模型可以快速得到单个设计变量和最大垂荡运动响应之间的关系，即当吃水增加或者垂荡板边长增加而其他变量不变时，最大垂荡运动响应逐渐减小，而立柱间距改变对垂荡运动变化影响较小.基于代理模型和多目标粒子群优化算法可以快速获得半潜平台的Pareto最优解，并且优化方案在满足约束的条件下，大大提升了平台的安全性和经济性.