基于OpenFOAM几何流体体积方法的波浪数值模拟

田 康，张 尧,李金龙，张新曙,3，尤云祥,3

(1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.自然资源部海洋减灾中心， 北京 100194；3.上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240)

在对波浪和结构物相互作用问题进行模拟时，如研究海洋平台立柱的波浪高阶力，船舶在波浪中运动的操纵性、耐波性等问题，为了保证数值结果的可靠性，需对波浪进行准确模拟.此外，在对波浪进行机理性研究时，如波浪非线性、波浪的传播与演化、波浪破碎等，也对波浪模拟提出了很高要求.

波浪模拟需要解决3个关键问题：造波、自由液面捕捉和消波.造波方法主要有3种：速度入口造波[1]、动边界造波[2]和源造波[3].速度入口法又称为边界输入法，即根据波浪理论，在每一时间步指定造波边界上速度场分布；动边界法又名仿物理造波法，即模仿模型试验中的推板造波法，通过边界运动推动计算域内的流体产生波浪；源造波法是一种在计算域内部产生波浪的方法，根据源项添加方式不同，可以分为动量源法和质量源法.

自由液面捕捉方法可以分为拉格朗日法和欧拉法.拉格朗日法从自由面处粒子运动入手，通过描述粒子运动轨迹来刻画自由液面变化，Harlow等[4]在1965年提出的MAC (Mark and Cell)方法就是其中一种代表方法.欧拉法关注自由液面附近某一固定空间区域流体流动变化，代表方法是Hirt 等[5]在1981年提出的流体体积(VOF)方法.根据求解过程的不同，VOF方法可细分为代数VOF方法和几何VOF方法，两者的区别在于：几何VOF方法会对自由液面进行几何重构，然后利用重构的自由液面更新体积分数率分布；代数VOF方法直接对体积分数率输运方程进行求解，不涉及任何几何对象的操作.传统几何VOF方法只适用于结构化网格，在推广到三维非结构化网格时遇到了困难，为了能够将几何VOF方法扩展到三维任意多面体网格，Roenby等[6]于2016年提出了一种新型几何VOF方法——isoAdvector方法.

消波主要有两种思路：出流边界消波和数值消波.出流边界是指采用人工截断边界，让流体自然地流出计算域边界而对计算内的求解没有任何影响，在众多方法中，Sommerfield辐射边界条件的效果最好[7].但是由于该条件在时间空间上是局部的，仅限于频率已知的规则入射波和长波情况[8].目前更为流行的方法是数值消波方法，数值消波方法分为3种：阻尼消波、主动式吸收消波和松弛区方法消波.阻尼消波通过在消波区域对自由边界条件或动量方程添加阻尼耗散项，从而达到消波效果；主动式吸收消波的原理是在水池末端设置推板，通过推板运动制造一个与反射波波幅相同但相位相反的波去抵消反射波，与此同时对入射波的传播没有任何影响；松弛区方法[9]消波是近几年提出的一种新型消波方法，其原理是在计算值和理论值之间合理分配权重，通过解析解与计算流体动力学(CFD)解之间的过渡实现消波.Chen等[10]在用OpenFOAM研究波浪-结构物相互作用问题时，使用了松弛区方法进行消波；此外，Jensen等[11]在对近海结构物多孔介质方程及阻力系数问题进行研究时也用到了松弛区消波方法.

本文研究基于开源流体力学计算平台OpenFOAM对波浪进行数值模拟.利用OpenFOAM已有几何VOF方法求解器InterIsoFoam(内置isoAdvector方法[6])，通过二次开发将InterIsoFoam与松弛区方法(Relaxation Zone Scheme)[12]消波结合，生成新的求解器WaveIsoFoam，对波浪进行模拟.首先采用几何VOF模拟波浪，并进行网格和库朗数收敛性分析，然后将计算结果分别与代数VOF方法及理论值进行了比较和分析，最后分析了松弛区方法中消波区长度和消波权重对波浪模拟的影响.

1 数学模型

在本文波浪模拟问题中，将气液两相视为单一不可压缩连续介质，并考虑流体黏性.控制方程、VOF方法和松弛区消波方法的介绍如下.

1.1 控制方程

在计算域中流体流动同时满足质量守恒定律和动量守恒定律，对应控制方程中连续性方程和Navier-Stokes方程的积分形式如下：

(1)

(2)

式中：V为计算域中任意网格；∂V代表组成网格的面的集合；ni,nj为网格表面对应单位法向量分量，其方向为指向网格外部；ui,uj为流体速度分量；ρ为流体密度；xi,xj,xk为笛卡尔坐标系下3个分量；μ为动力黏度；S为网格单元表面面积；pd为剔除静压之后的压力，总压力p的表达式为p=pd+ρgkxk；重力加速度g=[gigjgk]T=[0 0 -9.81]Tm/s2；源项fσ,i为表面张力，根据连续表面张力理论[13-14]，fσ,i可以用下式进行表达：

(3)

式中：表面张力系数一般取σ=0.078 2 kg/s2[14]；κ为界面曲率；α1为液体体积分数.

1.2 VOF方法

VOF方法通过引入流体体积分数对自由液面进行捕捉.流体体积分数定义为目标流体的体积与网格体积比值，基于这个函数在每个网格体心上的值，可以实现对运动的自由液面捕捉.在本文中，将液体和气体分别用下标1和2表示.两相流体域中单一流体密度ρ，动力黏度μ和运动黏度ν可以用下列公式表达：

ρ=α1ρ1+α2ρ2

(4)

μ=α1μ1+α2μ2

(5)

(6)

式中：ρ1,ρ2分别为液体和气体的密度；μ1,μ2分别为液体和气体的动力黏度；α1,α2分别为液体和气体的体积分数.

1.2.1isoAdvector方法 isoAdvector方法是Roenby等[6]在2016年提出的一种新型几何VOF方法.在每个时间步长内，isoAdvector方法的求解过程可以分为以下两步.

(1) 界面几何重构.当某一个网格单元所包含的液体体积分数在0和1之间时，该网格单元就称为界面网格单元，即自由液面经过这个网格单元.在界面几何重构中，关键是找出每个界面网格单元中，最适合划分液体和气体的平面(Isoface).Isoface需满足的条件为：从该网格单元(母网格单元)划分出的两个子网格单元的几何体积比值应与该网格单元体心所储存的液体体积分数匹配.搜寻最佳划分Isoface的具体方法可以参考文献[6].如图1所示，在相邻时间步长中，母网格内的Isoface会随着流体的输运而向某一方向移动.这些由Isoface所重构的界面将用于下一步体积分数更新.由于在寻找切分Isoface时是单独对每一个网格单元进行计算处理，所以重构界面可能并不连续[6].

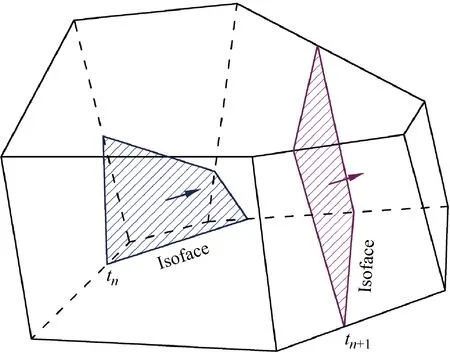
图1 Isoface在任意多面体网格单元中移动示意图Fig.1 Sketch of movement of Isoface within a polyhedral mesh

(2) 体积分数率更新.下一时刻体积分数场可由下式[15]得出：

(7)

(8)

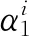
1.2.2代数VOF方法 代数VOF方法需要对体积分数输运方程进行求解，为获取更薄的界面厚度(定义液体体积分数为0.01～0.99的厚度)，在代数VOF方法中引入了人工压缩项.在OpenFOAM中，代数VOF方法采用MULES (Multidimensional Universal Limiter for Explicit Solution) 方法进行求解.MULES方法引入了FCT算法(Flux-corrected Transport Algorithm) 求解体积分数输运方程：

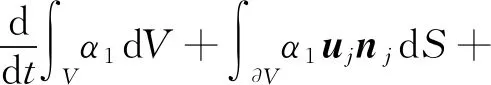
(9)

式中：等号左端最后一项为人工压缩项；uc,j的处理详见文献[15].

1.3 松弛区方法

松弛区方法的原理为：引入权重因子w，对松弛区内流体速度和体积分数进行加权，实现目标解析解和CFD计算解的过渡，从而实现速度入口造波边界和CFD计算域间的过渡，以及CFD计算域与压力出口边界的过渡，对应的表达式如下：

(10)

α=(1-w)αA+wαC

(11)

在入口处的松弛区，w从0以指定形式增长到1，实现解析解到CFD解的过渡；出口处的松弛区，w从1以指定的形式减小到0，实现CFD解到解析解的过渡，达到消波的效果，如图2所示.权重w的基本表达式为

图2 松弛区方法示意图Fig.2 Sketch of relaxation zone scheme

w=1-w*Co/Comax

(12)

式中：Co,Comax分别为局部库朗数和最大库朗数；w*有3种不同的形式，分别对应3种不同类型的权重分布，即指数权重、三阶多项式权重和自由多项式权重，

(13)

w*=-2(1-γ)3+3(1-γ)2

(14)

w*=1-γp

(15)

γ为松弛区域内的局部坐标，坐标位置取决于松弛区域的形状.需要说明的是，在所有情况中，松弛权重w*都是局部坐标γ下的函数，满足w*(γ=1)=0，w*(γ=0)=1；式(13)中指数p一般取3.5；式(15)中指数p一般取为整数.

2 结果与讨论

2.1 计算模型

本文基于OpenFOAM对波浪进行数值模拟.波浪模拟计算域如图3所示，全局笛卡尔坐标系(xi,xj,xk)原点O位于静水面、入口处垂直壁面和中纵剖面三面的相交处，xi轴方向与波浪传播方向一致，xk轴方向垂直向上，xj轴方向满足右手定则.计算域入口处及顶部边界条件为速度入口，出口处边界条件为压力出口；计算域底部为固壁边界条件，前后两侧为对称边界条件.在计算域入口处和出口处均设置了松弛区，其中入口处松弛区长度为两个波长；出口处的松弛区长度设置对消波效果有影响，具体长度选取见后文关于消波问题的分析.在计算域自由液面处沿xi轴均匀分布320个波高监测点，用于获取波浪在数值模拟过程中的空间数据和时历数据.计算域长度为20 m,宽度为1 m，高度为3 m，计算域水深为2.5 m,实际计算水深为5 m.

图3 三维计算域示意图(m)Fig.3 3D sketch of computational domain (m)

本研究数值模拟应用开源软件ESI OpenFOAM-v1812，基于层流理论[16-17]，使用WaveIsoFoam对两相流进行求解.WaveIsoFoam是在interIsoFoam求解器基础上引入松弛区功能修改得到.InterIsoFoam内置了isoAdvector方法对自由液面进行捕捉，因此代表了几何VOF方法求解两相流.

时间离散格式采用二阶Crank-Nicolson方法，对流项采用高分辨率Gauss vanLeer求解，Laplace项采用高斯线性修正方法进行求解；控制方程解耦采用SIMPLE方法，动量方程用Gauss-Seidel方法求解.在每个时间步长内，有两次压力修正，分别应用GAMG求解器和PCG求解器对这两次压力修正时的压力泊松方程进行求解.

2.2 收敛性分析

在实际对波浪相关问题进行模拟研究时，为了尽可能减小由于数值计算产生的误差，同时尽可能提高计算效率，需先进行网格和库朗数收敛性分析.为了探究几何VOF方法在收敛性方面的特性，本文选用了无限水深Stokes五阶波浪进行分析，波浪模拟参数见表1.

表1 Stokes五阶波波浪模拟参数Tab.1 Simulation parameters of Stokes fifth-order waves

2.2.1网格收敛性分析 为了能够较好地模拟波浪传播，需要在自由表面处进行网格加密.一般来说,在横向、纵向和垂向3个方向中，垂向网格密度对波浪模拟的影响尤为明显.因此，在自由液面处，固定垂向网格尺寸与纵向(波浪传播方向)网格尺寸比为1∶2，在垂向选取4组网格H/Δz=6,8,12,16(H为波高，Δz为垂向网格尺寸).图4所示为模拟时间为30 s时不同网格密度下波高的空间分布，图中：xi为沿计算域纵向方向的距离；η为波高.由图可知，当网格密度H/Δz>8时，几何VOF方法能较好地对波浪进行模拟；而当H/Δz<8时，几何VOF方法模拟波浪在波高和相位上随着波浪传播逐渐与理论解产生偏离.因此，在使用几何VOF方法对波浪进行模拟时，单个波高垂向分布网格层数至少应为8层.

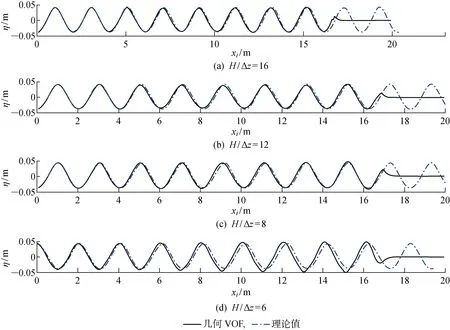
图4 不同网格密度下波高的空间分布Fig.4 Spatial distributions of wave elevations at different mesh densities

2.2.2库朗数收敛性分析 库朗数定义如下：

(16)

式中：Δt为时间步长；|U|为某个网格单元内速度矢量的模，Δx为速度方向网格长度.在计算域网格已划定的情况下，网格长度Δx确定；在同一工况下，固定位置的速度矢量的模|U|也确定.因此，可以用库朗数Co对CFD计算的时间步长Δt进行反映.用于收敛性分析所选取的库朗数Co=0.1,0.2,0.4,1.0，图5为模拟时间为30 s时不同库朗数下波高空间分布.

图5 不同库朗数下波高的空间分布Fig.5 Spatial distributions of wave elevations at different Courant numbers

计算结果显示，不同库朗数下波浪模拟结果均能较好地与理论结果相吻合.即在使用几何VOF方法进行波浪模拟时，选取较大的库朗数或时间步长，也能得到较为满意的结果.

2.3 造波分析

图6为模拟时间为30 s时不同波陡下几何和代数VOF方法波高模拟空间分布，其中波高为H、波长为λ、波陡为δ.图7为模拟时间为30 s时图6对应的波高模拟时历曲线.从图6和图7中可以看出：

图6 不同波陡下几何和代数VOF方法波高模拟空间分布Fig.6 Spatial dstributions of wave elevations by using geometrical and algebraic VOF methods at varied wave steepnesses

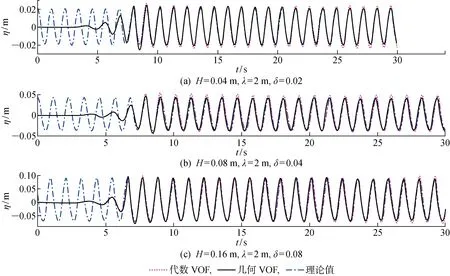
图7 不同波陡下几何和代数VOF方法波高模拟时历曲线Fig.7 Time histories of wave elevations by using geometrical and algebraic VOF method at varied wave steepnesses

(1) 对于波高的空间分布和时历模拟，在不同波陡情况下，相比于代数VOF方法，几何VOF方法都能得到更准确的结果；在相同设置下，代数VOF方法模拟得到的波高则稍大于理论值得到的波高；

(2) 波浪在空间域传播时，无论是几何VOF方法还是代数VOF方法，产生的波浪均会与理论结果产生微小的空间相位差，且随着模拟波浪的波高增大，空间相位差也逐渐累积变大；波浪在时间域中，随着模拟时间增加，模拟结果与理论结果无相位差产生，同时不受模拟波浪波高变化的影响.

图8为模拟时间为30 s时不同波频下几何和代数VOF方法波高模拟空间分布，其中波频用ω表示.比较结果显示，对于不同的波浪频率，几何VOF方法均能给出较好的波浪模拟结果.相比之下代数VOF方法在不同波浪频率情况下模拟波浪的空间相位与理论值吻合较好，但幅值略大于理论值.

图8 不同波频下几何和代数VOF方法波高模拟空间分布Fig.8 Spatial dstributions of wave elevations by using geometrical and algebraic VOF method at varied wave frequencies

几何VOF方法相较于代数VOF能更加精确地模拟波浪，其中最主要的原因在于几何VOF方法在求解体积分数之前对网格进行了重构，使其能够更加精确地自由液面进行捕捉.图9为几何VOF方法和代数VOF方法分别对应的自由液面处液体体积分数分布情况，蓝色部分代表α1=0 (气体)，红色部分代表α1=1 (液体)；黑线α1=0.01，黄线α1=0.99.用液体体积分数为0.01和0.99两个分界之间的厚度以表示自由液面捕捉精度，可以看到几何VOF方法所得的自由液面处液体分布更为集中，即界面厚度比代数VOF方法更小.这体现了几何VOF方法较代数VOF方法有更高的自由液面捕捉精度，即能更好地对波浪进行模拟.

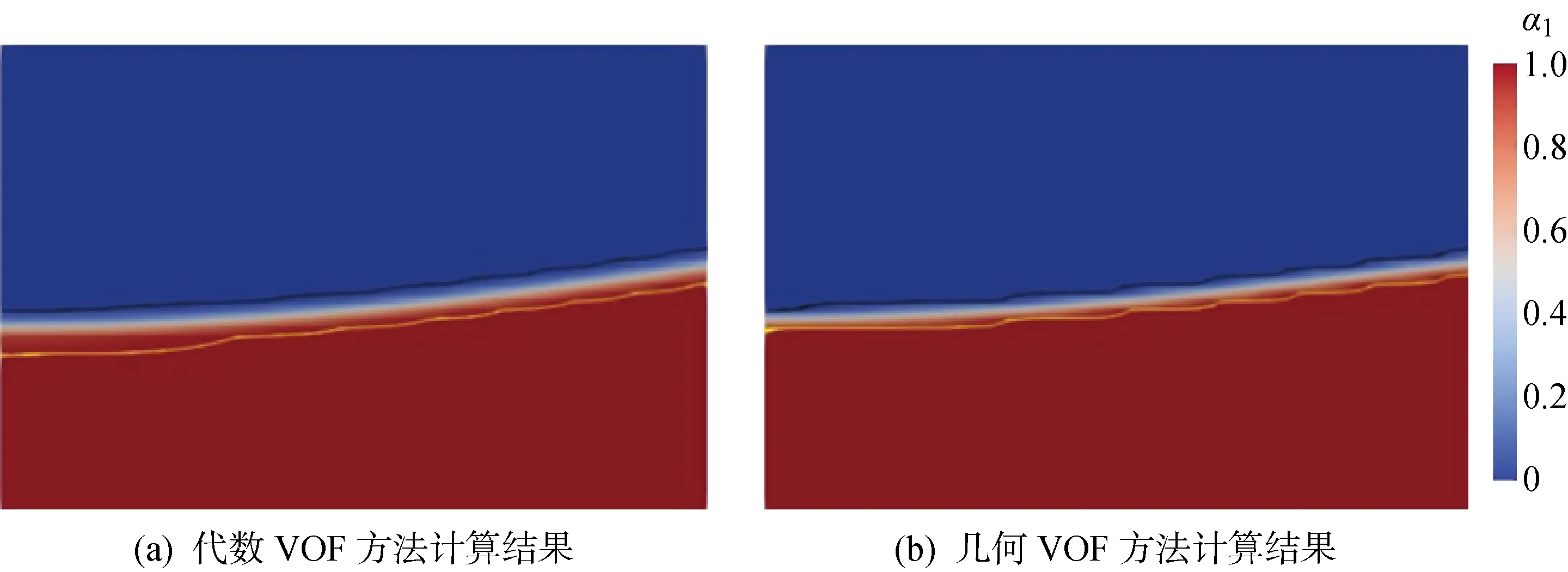
图9 自由液面处液体体积分数α1分布情况Fig.9 Distributions of the liquid volume fraction α1 around free surface

2.4 消波分析

为了能够模拟出质量较高的波浪，除了需要选择合适的网格密度、库朗数和自由液面捕捉方法以外，消波方法的选择也非常重要.若消波效果不好，可能会导致波浪反射从而对入射波造成干扰，使得波浪模拟结果与理论结果发生偏离.

在前面介绍中已经提到，本次研究所采用的消波方法为松弛区方法.在松弛区方法中，消波区长度和消波加权方法会对消波效果有较为明显的影响.因此，在本次研究中，分别对这两个因素进行研究和分析.

2.4.1消波区长度分析 在消波区长度对消波效果影响的研究分析中，选取1倍波长(2 m)、2倍波长(4 m)和3倍波长(6 m)进行模拟计算，消波权重采用指数方法，即式(13).图10为模拟时间为30 s时不同消波区长度(用Lwaz表示)下波高空间分布，两条红色垂向虚线间的距离为波高削减至零所需最短空间长度.

图10 不同消波区长度下波高空间分布 Fig.10 Spatial distributions of wave elevations at different lengths of relaxation zone

从图10中可以看出，随着消波区长度增加，波幅削减至0所需最短空间长度也随之增加，这是由计算解至解析解过渡区域延长所致.但是最短空间长度占总消波区长度比值较小，说明松弛区方法可以快速地对波高进行抑制.

而在波浪反射方面，从图10(a)中看出，当消波区长度为一个波长时，靠近消波区附近的波高模拟结果明显高于理论值，说明波浪反射未得到完全遏制.而2倍和3倍波长的消波区长度，不仅能够实现快速消波，并且能很好地遏制波浪反射.

2.4.2松弛区消波权重分析 松弛区消波方法有3种权重控制流体速度和体积分数率从边界到CFD计算域的过渡，分别是：指数方法(式(13))、三阶多项式方法(式(14))以及自由多项式方法(式(15)).图11为选取消波区长度为2倍波长、模拟时间为30 s时不同消波权重下波高空间分布.比较发现，相比于指数方法进行权重分配，三阶多项式及自由多项式方法，均能在非常短的区域内，将波幅削减至0；但波幅模拟结果都大于理论值，说明两种权重分配方法都不是最佳过渡方式，不能很好地遏制波浪反射.虽然指数方法将波幅削减至0所需最短空间长度略大于后两种方法，但能更充分遏制波浪反射，得到最为精确的波浪模拟结果.综合考虑，在使用松弛区方法进行波浪消波处理时，应当优先选择指数法方法作为权重分配方法.

图11 不同消波权重下波高空间分布Fig.11 Spatial distributions of wave elevations at different weights of wave absorption

3 结论

本次研究基于OpenFOAM，对Stokes五阶波进行了模拟分析，着重研究了几何VOF方法及松弛区方法在波浪模拟中的应用.

在网格和库朗数收敛性分析中发现，若要模拟出较为满意的波浪，在一个波高范围内至少垂向设置8层网格，库朗数可取Co=1.在不同波陡的波浪模拟中，引入了代数VOF方法，将之与几何VOF方法的模拟结果和理论值进行比较发现：两种VOF方法模拟的波浪均会产生较小的空间相位差，而几何VOF能够更好地对波高进行模拟.在不同波频模拟中，几何VOF方法能较好地对不同波频下波高及空间相位进行模拟；代数VOF能较好地对相位进行模拟，而波高结果则略大于理论值.通过对比几何和代数VOF方法下自由液面处液体体积分数分布情况，可知几何VOF之所以较代数VOF方法有更高的波浪模拟精度，是因为几何VOF方法通过网格重构有效减少了伪扩散现象.

在松弛区方法消波的研究中，对消波区长度及权重方法进行了分析.对于消波区长度，较短消波区长度虽足够以波幅削减至0，但不能很好地遏制波浪反射.因此，需要选取适当的消波区长度(2倍波长及以上)，以确保能遏制波浪反射，从而避免对入射波的模拟产生影响.在权重分布的选择上，相比于三阶多项式权重及自由多项式权重，采用指数方法进行权重分配的消波效果最好.