考虑三维圆柱铰间隙碰撞的空间机构柔性多体动力学分析方法

姚廷强, 陈锐搏, 王立华, 刘孝保

(昆明理工大学 机电工程学院,昆明 650093)

高精密空间机构和工业机器人的旋转铰通常由销轴和轴套的相对运动构成，其动态性能对机构系统的运动精度和动力学特性等有着至关重要的影响，其内部的接触分析一直是众多学者关注的问题[1-3]。由于销轴和轴套之间存在径向和轴向的间隙碰撞作用，引起旋转铰内部作用力的变化，造成构件的弹性变形和动态应力的突变，产生振动和噪声，加剧机构运动副的磨损，降低了机构系统的运动精度、工作效率和疲劳寿命。多体系统动力学中关节效应模型的研究备受重视，取得了较大进展，主要对平面多体系统中二维旋转铰内部接触研究，考虑间隙碰撞、润滑和摩擦磨损等关键因素。

Flores等[4-6]开展了平面多刚体系统中旋转铰的间隙碰撞动力学方法研究和试验测试分析，考虑润滑、多间隙、结构参数、工况条件等因素对系统动力学特性的影响分析。Tian等[7]运用绝对节点坐标法，研究平面多柔性体系统中旋转铰的间隙碰撞和摩擦润滑动力学方法。Bai等[8]基于Hertz接触理论，建立含多个旋转铰内部间隙的平面四杆机构多刚体力学模型。Zhao等[9]运用平均雷诺方程描述考虑描述粗糙度的润滑表面之间的油膜特性，建立了考虑间隙和润滑的旋转铰接触力学模型。Zheng等[10]考虑间隙和润滑的旋转铰和球铰接触力学模型，分析间隙、输入转速和冲裁力对多柔性连杆的超精密压力机多体动力学特性的影响。Daniel等[11]研究了滑动轴承的流体动力作用的气穴边界积分方法，分析了含间隙和滑动轴承的平面机构动力学响应特性。Reis等[12]基于Hertz接触理论和库伦摩擦定律，研究含间隙平面曲柄滑块机构的流体润滑动态特性。Li等[13]考虑两个间隙旋转副和连杆的弹性变形，对比分析谐响应驱动下平面曲柄滑块机构的动态响应。Ben Abdallah等[14]运用ADAMS软件建立了含多柔性连杆和多间隙旋转副的平面曲柄滑块机构动力学仿真模型，分析了三种不同旋转副的接触力学模型下的动力学特性。王庚祥等[15]基于连续接触模型，研究空间球面副间隙对新型减振平台动力学性能影响。占甫等[16-17]考虑三维间隙铰的轴向和径向间隙，采用几何构形，构造三维间隙铰节点接触判别条件，数值计算和实验测试了含三维间隙铰节点可展机构的动力学特性。Flores等[18-20]研究了含润滑球铰的空间多刚体机构的动力学特性；建立三维旋转铰的销轴和轴套的连续接触力模型，计算空间双摆的接触-冲击多刚体动力学响应；运用ADINA建立含间隙和润滑的三维圆柱铰接触力学模型，分析了其弹性流体动力润滑特性。Tian等[21-24]采用自然坐标法和绝对节点坐标法，研究了含间隙和润滑的三维圆柱铰和球铰的接触力学模型，对比分析了理想铰、干摩擦铰和流体润滑铰下空间机构的动力学特性。基于Hertz点接触力学模型，Lankarani等[25]考虑两物体表面发生接触时的能量耗散特性，提出两物体表面发生点接触时的的恢复系数非线性弹簧阻尼力学模型。赵刚练等[26]基于空间解析几何与矢量计算，提出圆柱铰的接触分离切换点的判断方法，研究三维圆柱铰的多刚体动力学特性。刘太素等[27]针对空间圆柱铰的轴向和径向接触模式，开展几何和运动分析，提出一种改进的计算潜在接触点位置的方法，研究了圆柱铰系统的多体刚体运动精度和动力学分析。上述多数文献通常采用Lankarani和Nikravesh提出的连续力学模型或迟滞接触模型，处理旋转铰的间隙接触碰撞作用。该模型通常适用于平面旋转铰的圆-圆接触或三维球-球椭圆接触区域的点接触，其不能精确描述三维间隙圆柱铰的圆柱-圆柱接触问题和接触长度问题[28-29]。

在含间隙机构的动力学模型、运动副分离准则、混沌特性、优化设计等方面的基础性工作还不够成熟。考虑三维圆柱铰的间隙碰撞作用、动态接触关系、流体润滑、摩擦磨损等关键因素的空间机构动力学研究还处于探索阶段，尚需系统深入的研究，为复杂工况下高精度多间隙三维圆柱铰-机构系统动力学分析和动态设计提供新方法。

1 三维圆柱铰的接触力学模型

1.1 三维圆柱-圆柱相互作用关系

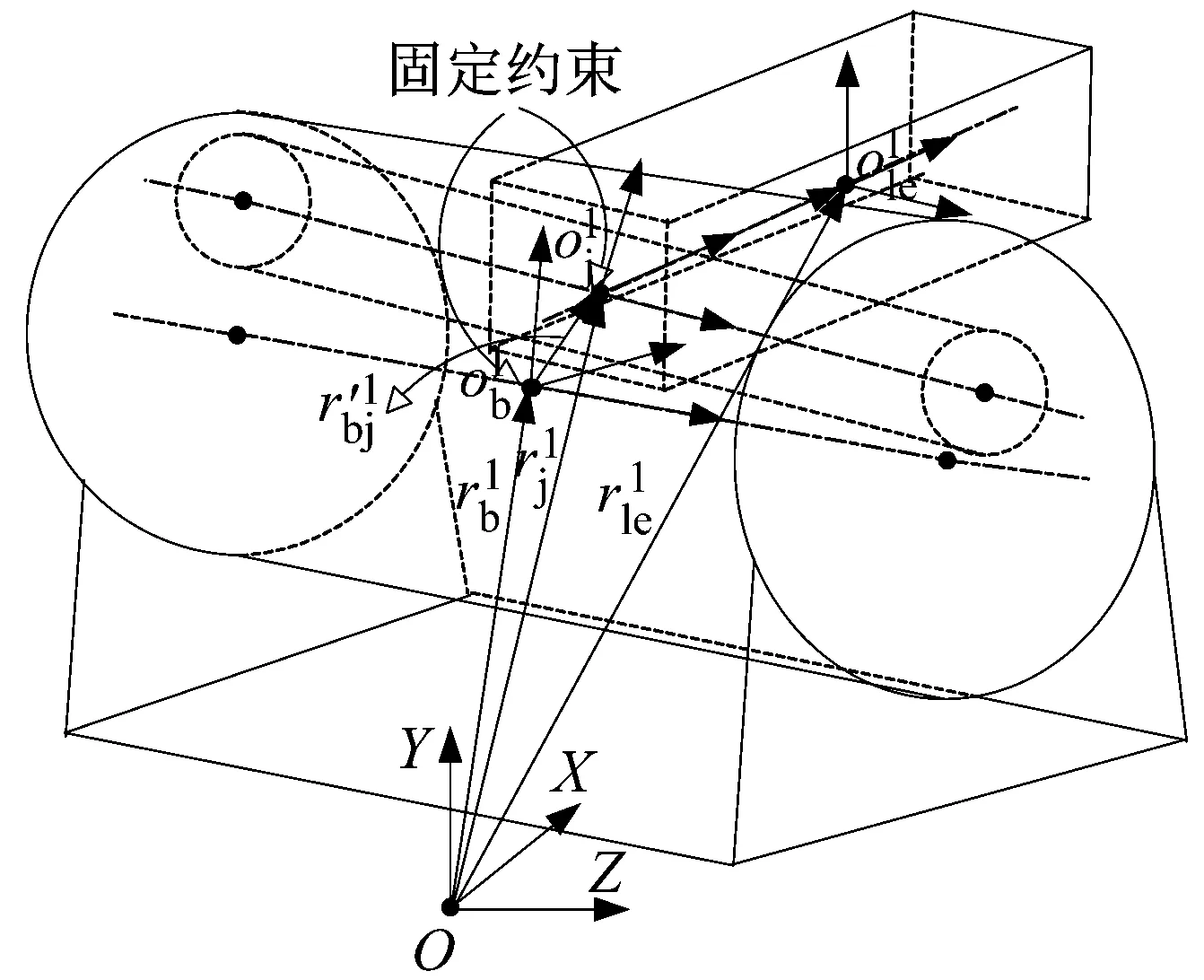
图1和图2为含三维圆柱铰的空间机构模型和三维圆柱铰示意图。工程实际中空间机构的三维圆柱铰通常由圆柱销轴和带圆柱型孔的轴套组成，销轴与轴套之间存在径向间隙和轴向间隙，从而使得实际轴销与轴套在铰接点是三维间隙接触关系。本文忽略销轴和轴套之间的轴向相对移动，采用三维圆柱-圆柱线接触方法模拟三维空间圆柱铰的持续接触、间隙碰撞和摩擦作用。

图1 含三维圆柱铰的空间机构模型

(a) 圆柱-圆柱的三维接触模型

(b) 圆柱铰1

(c) 圆柱铰2

(1a)

含三维圆柱铰的空间机构系统的广义坐标q为

(1b)

图2(a)为圆柱-圆柱的三维接触模型。圆柱滚子的切片法是计算滚子轴承中沿滚子与滚道接触线的负荷分布的一种数值计算法[30-31]。本文采用切片法将销轴沿轴线均匀地切成若干相互独立的薄圆片，假设在负荷作用下计算圆片与轴套的接触变形时，各圆片是相互独立的，没有切应力作用，变形后各圆片的中心仍保持在销轴的中心线上。

要确定销轴表面上P点与轴套的相互作用，首先应确定销轴中心与轴套中心的位置和含有P点的圆片相对于轴套中心的位置。由图2(a)可知，在惯性坐标系下，销轴的位置矢量为

(2)

则销轴中心与轴套中心之间的相对位置为

(3)

将销轴沿着轴线zj方向切片为若干圆片，在销轴体坐标系下的zj方向上圆片k中心的轴向位置为

(4)

(5)

式中,Abj为销轴体坐标系与轴套体坐标系之间的方向变换矩阵。

(6)

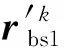
定义Abs为轴套体坐标系到切片方位坐标系的方向变换矩阵，可得Abs=Abs(0,0,φ)。

在销轴体坐标系下圆片k上的P点相对于销轴中心的位置为

(7)

式中,Rj为销轴半径;ϑ为P点在销轴体坐标系xjyj平面内的方位角，确定P点在销轴表面上的角位置。

在切片方位坐标系中P点相对于轴套中心的位置为

(8)

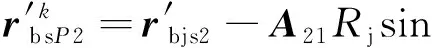
(9)

由于销轴为轴对称几何体，则方位角ϑ为

(10)

因此，销轴圆片k与轴套的接触穿透量δk为

(11)

式中:δk为负值，表示销轴圆片k与轴套发生接触;δk为正值，表示不接触。

1.2 动态接触力

三维圆柱铰内部实质上是销轴和轴套之间的三维圆柱-圆柱动态接触关系，属于三维圆柱体之间的弹性接触问题。精确的三维间隙圆柱-圆柱接触力学模型还处于探索研究阶段。根据Hertz接触理论，圆柱与圆柱的相互作用可以由Hertz线接触关系描述。本文采用圆柱与圆柱的线接触方法，计算圆柱与圆柱的接触变形量，建立圆柱铰的轴销与轴套之间的三维动态间隙接触作用。由于线接触问题的弹性趋近量δ没有准确解，常用Palmgren给出线性趋近量公式描述圆柱-圆柱线接触载荷和接触弹性变形量之间的关系。

(12)

当计算获得两个圆柱体的接触弹性变形量，则接触力为

F=Kδ10/9

(13)

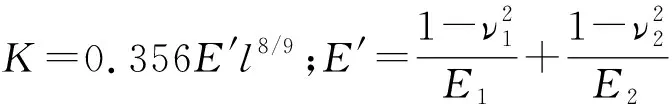
当两圆柱体为钢材料时，接触刚度K为

K=7.86×104l8/9

(14)

因此，基于Hertz线接触力学模型和罚函数法，引入三维圆柱-圆柱接触过程中的耗散阻尼作用，由接触穿透量式(11)，可得销轴圆片k和轴套之间发生接触时的法向接触力显示表达式为

(15)

根据Coulomb摩擦定律，销轴圆片k和轴套之间的摩擦力与法向接触力间的关系为

(16)

图3为销轴与轴套接触过程中摩擦因数与相对速度的关系，则摩擦因数为

(17)

式中:havsin(…)半正弦函数描述了摩擦因数从静摩擦因数μs到动摩擦因数μd的平滑非线性变化；vk为发生Hertz接触作用时接触点P处的相对切向速度；vs和vd分别为静摩擦和动摩擦的临界速度。

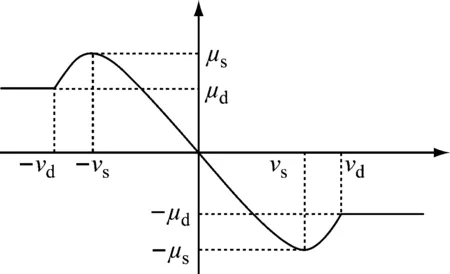
图3 摩擦因数与相对速度关系

2 含三维圆柱铰的空间机构动力学模型

2.1 柔性体的刚性有限元方法

根据刚性有限元方法(Rigid Finite Element Method)[32]，柔性杆件的等效方法是将柔性杆件离散为m个等效刚体单元和m-1个TB(Timoshenko Beam)单元，以TB单元连接等效刚体单元模拟杆件的结构弹性变形和阻尼特性，以等效刚体单元模拟杆件的质量、惯量特性和几何特性。

(18)

由于柔性杆件的TB单元的刚度矩阵仅与TB单元的几何参数和材料属性等因素有关，与外载荷无关。

图4 柔性连杆的等效刚体单元模型

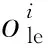
(19)

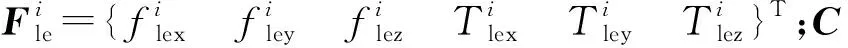
Timoshenko梁单元的刚度矩阵为

(20)

式中:K11=EA/L，K22=12EIzz/L3(1+Py)，K33=12EIyy/L3(1+Pz)，K44=GIxx/L，K55=(4+Pz)EIyy/L(1+Pz)，K66=(4+Py)EIzz/L(1+Py)，K26=-6EIzz/L2(1+Py)，K35=6EIyy/L2(1+Pz)，Py=12EIzzSy/GAL2，Pz=12EIyySz/GAL2;Sy，Sz为Timoshenko梁在y和z方向上的剪切变形修正因子，方形对称截面的梁单元的修正因子通常取值为1.2。

2.2 空间机构多体动力学方程

以图1和图2(b)、(c)所示的双连杆空间机构为例，本文忽略销轴和轴套之间的轴向相对移动，空间机构中的两个圆柱副约束实质上转换为旋转约束，采用销轴与轴套之间的旋转副约束描述。当采用销轴和轴套之间的三维圆柱-圆柱接触作用时，则消除此类旋转副约束。各零部件初始位置的体坐标系均与惯性坐标系的方向一致，且轴套1的体坐标系与惯性坐标系重合，则空间机构系统的约束方程为

(21)

轴套1体坐标系与惯性坐标系重合，则轴套1中心与机架的固定约束方程为

(22)

(23)

当圆柱铰1为理想旋转约束时，销轴1与轴套1初始位置为轴线共线，体坐标系重合，则理想铰1的旋转约束方程为

(24)

当圆柱铰2为理想旋转约束时，销轴2与轴套2初始位置为轴线共线，体坐标系重合，则理想铰2的旋转约束方程为

(25)

(26)

(27)

因此，双连杆空间机构系统的动力学方程为

(28)

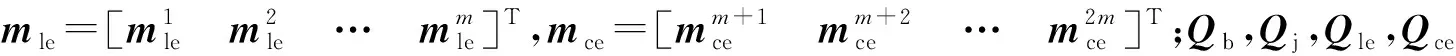
由此可得空间机构系统的一般动力学方程为

(29)

对空间机构系统的微分代数方程组式(28)进行数值计算求解，计算作用在各零件上的作用力和力矩，各瞬时点的位置和运动参数，可得含三维圆柱铰的空间机构的动力学结果。

3 空间机构实例计算及结果分析

3.1 三维间隙圆柱单铰接触对比分析

如图1所示的双连杆空间机构系统，两个连杆采用刚体有限元方法描述为柔性体，连杆与机架、连杆与连杆采用空间圆柱铰连接，详细参数见表1空间机构的结构参数与材料、力学参数所示。

本文忽略圆柱铰的轴向接触作用，假设轴销与轴套无轴向相对位移。为了验证本文提出的三维间隙空间圆柱铰的计算方法，开展圆柱铰的载荷平衡模拟，对比分析圆柱铰:①受一端径向力作用(单点接触作用);②受中心旋转扭矩作用(双点接触作用);③受中心径向力作用(线接触作用);④受中心径向力与扭矩联合作用(混合接触作用);⑤受中心径向力、扭矩和一端径向力作用下(混合接触作用)等5种工况下的接触力。图5～图9分别为在径向间隙1 mm，中心径向力和端部径向力均为-Y方向的1 000 N，中心旋转扭矩为绕X方向的10 N·m作用下，三维间隙圆柱铰的接触力结果。

表1 空间机构的结构参数与材料、力学参数

图5为圆柱铰端部受径向力作用下的单点接触力(①工况)。销轴受载端与轴套之间先发生接触，而在重力和不平衡力作用下，销轴非受载端与轴套后发生接触碰撞。由于存在径向间隙，在非受载端未发生接触碰撞时，销轴与轴套之间发生持续单点接触现象，接触力大小为所施加载荷。销轴非受载端与轴套之间的碰撞力随着接触次数的增加而减小，随后逐渐达到稳定。非受载端的接触碰撞作用对销轴与轴套之间的单点接触力的变化规律有着重要的影响。图6为三维圆柱铰受中心旋转扭矩作用下的双点接触力(②工况)。销轴两端与轴套之间发生持续双点接触现象，且销轴两端部的等效接触法向力相等，作用方向相反，因此销轴受到的接触合力为销轴自身重力。图7为三维圆柱铰受中心径向力作用下的线接触力(③工况)。销轴与轴套之间发生持续线接触现象，且销轴两端部的等效接触法向力相等，作用方向相同，因此销轴受到的接触合力为所施加载荷和销轴自身重力。

图8和图9分别为销轴受不同载荷联合作用下的接触合力和接触法向力(④和⑤工况)。对比分析图7、图8和图9可知，中心旋转扭矩对销轴与轴套之间的接触合力无影响，对销轴两端部的接触法向力有等幅值的增加或减小作用。端部径向力对销轴与轴套之间的接触合力和受载端部的接触法向力都有重要的影响。由于算列中端部径向力和中心径向力方向相同，因此销轴的接触合力和受载端部的接触法向力均以施加载荷1 000 N幅值增大，而非受载端的接触法向力保持不变。计算分析结果表明提出的三维间隙圆柱铰的计算方法能很好的计算模拟圆柱铰的单点、双点和线接触现象，获得较好的接触力计算精度。

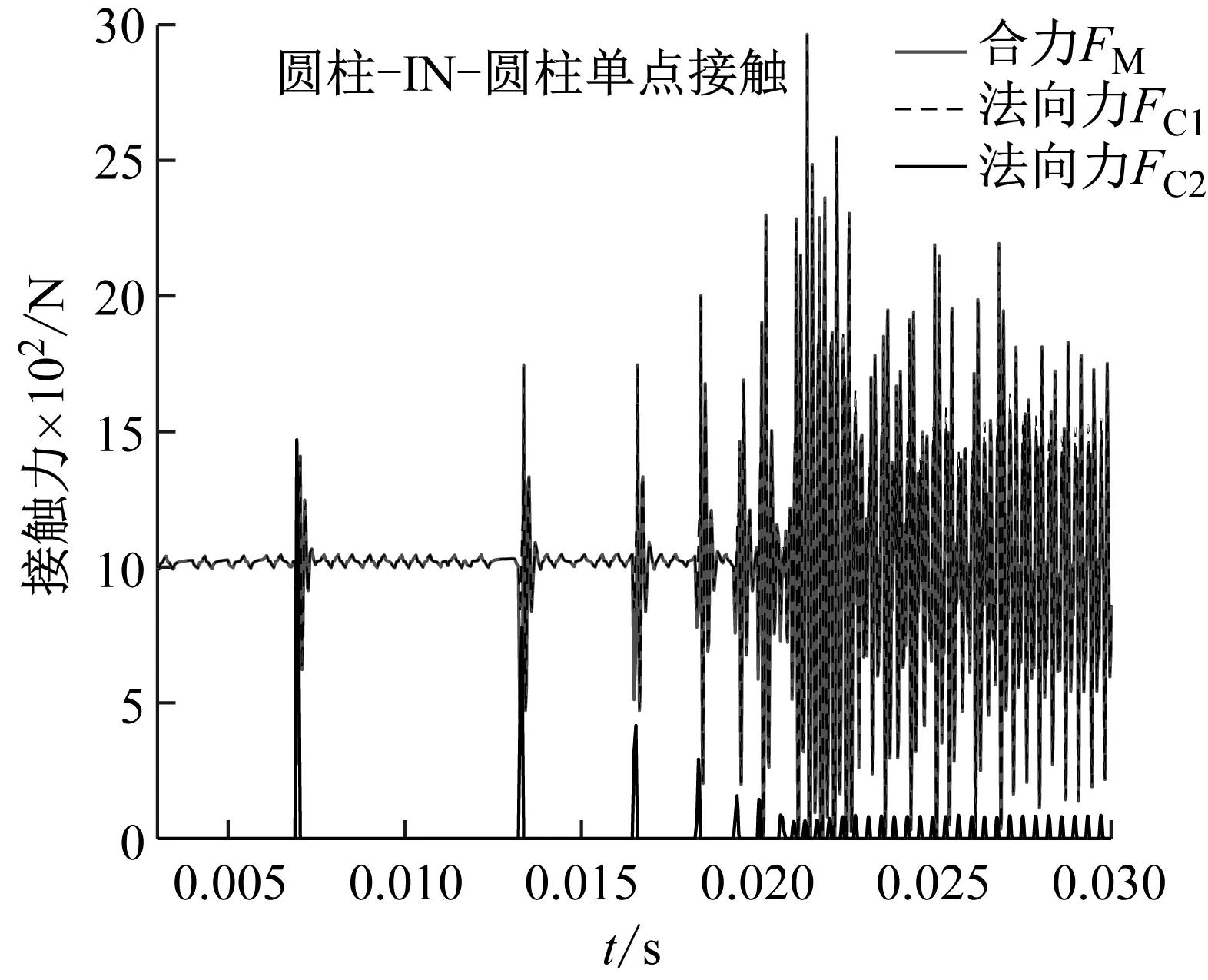
图5 三维圆柱铰一端受径向力作用下的单点接触力

图6 三维圆柱铰受中心旋转扭矩作用下的双点接触力

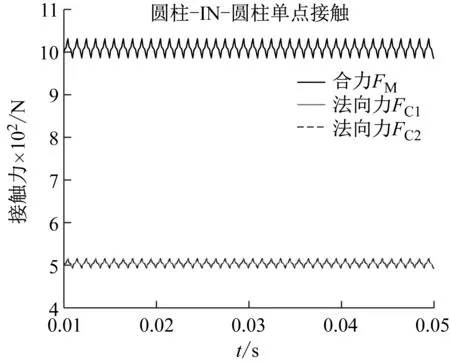
图7 三维圆柱铰受中心径向力作用下的线接触力

3.2 三维间隙圆柱铰内接触作用对系统动态响应的影响

以空间机构仅受重力作用，分别计算3种不同模型下空间机构的动态响应结果：①理想铰为刚性连杆，销轴与轴套位置采用理想的旋转副约束模型；②刚性连杆-圆柱铰为刚性连杆，销轴与轴套位置为实际的三维圆柱-圆柱接触作用模型；③柔性连杆-圆柱铰为柔性连杆，销轴与轴套位置为实际的三维圆柱-圆柱接触作用模型。

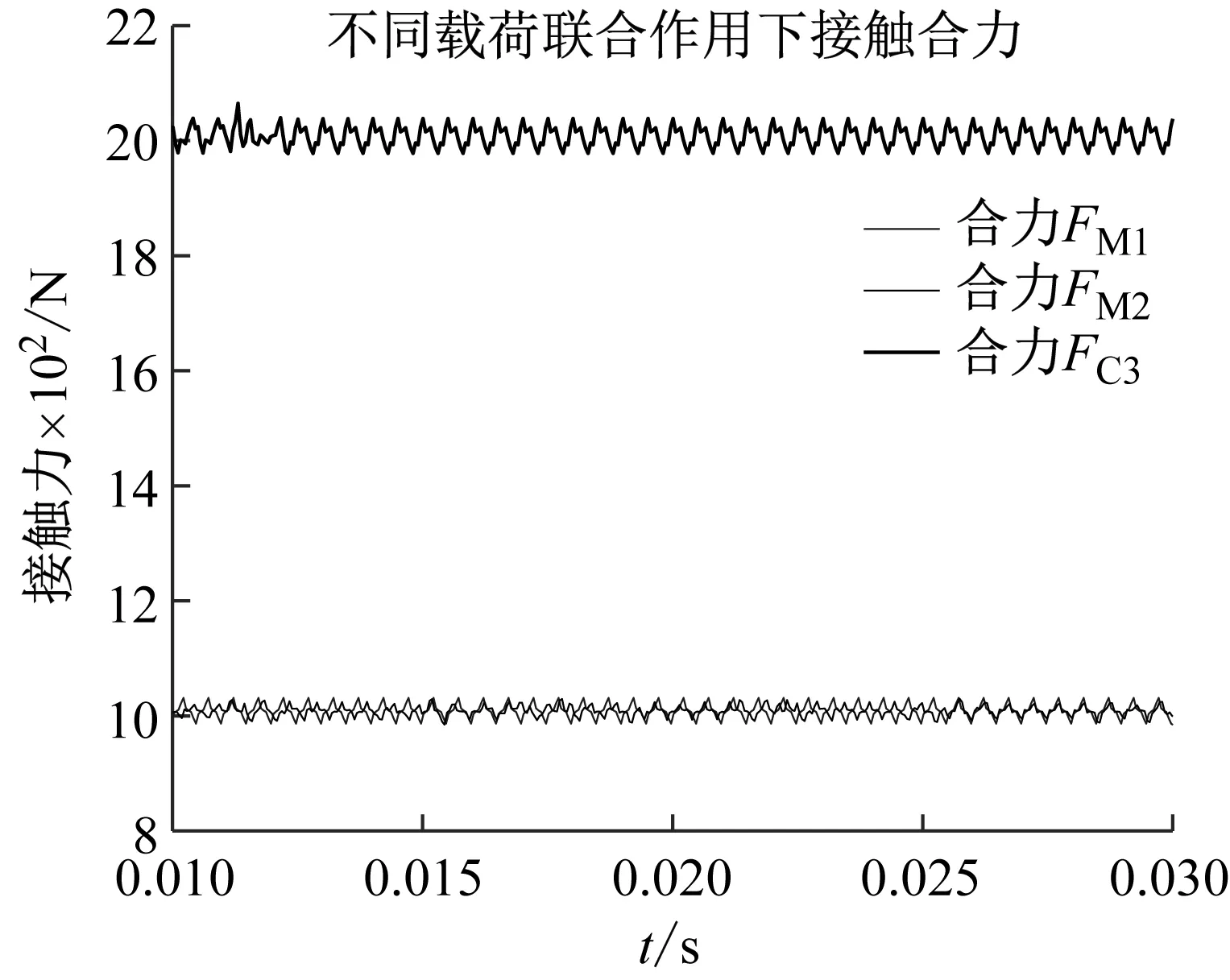
图8 不同载荷联合作用下三维圆柱铰的接触合力

图9 不同载荷联合作用下三维圆柱铰的接触法向力

图10为不同模型下A点的Y向位移，分别计算了理想铰、刚性连杆-无间隙圆柱铰、刚性连杆-有间隙圆柱铰和柔性连杆-有间隙圆柱铰下的A点的Y向位移响应。图11和图12分别为理想铰、刚性连杆-无间隙圆柱铰(圆柱铰无间隙)和柔性连杆-有间隙圆柱铰(圆柱铰有间隙)下A点在X-Y平面和Z-Y平面上的运动轨迹。分析可知，考虑三维圆柱铰动态接触关系的空间机构模型与理想铰的位移或运动轨迹的变化规律总体相似。由于理想铰模型忽略了连杆的弹性变形和三维圆柱铰的间隙碰撞的影响，Y向的位移结果存在一定的误差。刚性连杆-无间隙圆柱铰的Y向位移与理想铰的理论位移结果比较接近，由于三维圆柱铰存在圆柱-圆柱的动态接触，在位移极值波峰波谷位置存在一定的差异。由于三维圆柱铰的间隙碰撞影响，在连杆首次下降和上升过程中刚性连杆-有间隙圆柱铰和柔性连杆-有间隙圆柱铰的Y向位移与理想铰相同，而在位移极值波峰波谷位置和其余下降过程中的Y向位移的差异相对较大。同时考虑连杆的弹性变形和三维圆柱铰的间隙接触碰撞关系，柔性连杆-有间隙圆柱铰模型较为真实地模拟空间机构的动态响应。

图10 不同模型下A点的Y向位移

图11 不同模型下A点在X-Y平面的运动轨迹

图12 不同模型下A点在Z-Y平面的运动轨迹

图13为无间隙圆柱铰下空间机构在圆柱铰位置处的作用力。图14为有间隙双圆柱铰下空间机构在圆柱铰1位置处的作用力。分析可知，由于空间机构仅受重力作用，无间隙时三维圆柱铰的圆柱-圆柱连续接触，无碰撞现象，圆柱铰内的动态接触力与理想铰的约束反力变化规律相同，且幅值也几乎相同，柔性连杆-无间隙圆柱铰模型存在较小的波动差异。有间隙时，三维圆柱铰的圆柱-圆柱存在持续接触和间隙碰撞两种典型的动态接触现象。当圆柱-圆柱存在持续接触作用时，动态接触力的大小及变化规律与理想铰的约束反力相近。当圆柱-圆柱存在间隙碰撞作用时，三维圆柱铰内存在较大幅值的碰撞力，且空间机构在下降过程比上升过程出现间隙碰撞作用的更频繁。首次下降过程中，柔性连杆-圆柱铰比刚性连杆-圆柱铰的碰撞力相对小些，其余下降过程中的碰撞力相对更大。由此可知，忽略连杆的弹性变形和三维圆柱铰的动态间隙接触碰撞作用，将高估空间机构的运动精度，低估其运动副的相互作用力，从而影响空间机构的动态设计和疲劳寿命预测。

图13 不同模型下无间隙圆柱铰的作用力结果

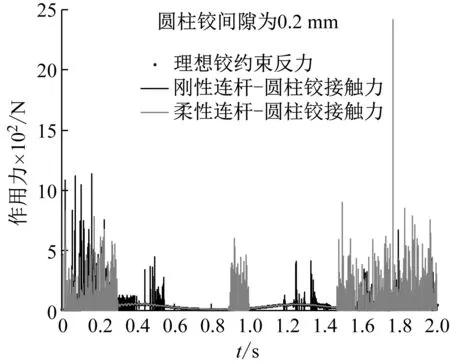
图14 不同模型下有间隙双圆柱铰的作用力结果

图15为不同模型下有间隙圆柱铰的圆柱的左右端的相对运动轨迹。由图1所示，连杆ce位于连杆le的右侧(+Z方向)，连杆不同刚度对三维圆柱铰的左端(-Z方向)的销轴和轴套的相对运动轨迹的影响较小，对右端(+Z方向)的相对运动轨迹的影响较大，左端为部分圆形的周期运动轨迹，右端为不规则的非周期运动轨迹。

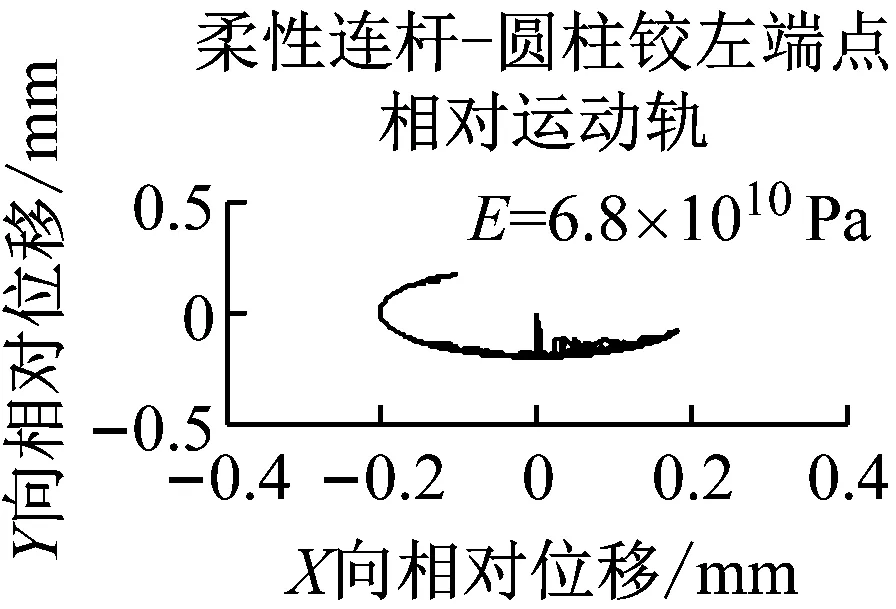
图15 不同模型下有间隙圆柱铰的圆柱端点相对运动轨迹

3.3 三维间隙圆柱铰内摩擦作用对系统动态响应的影响

以图1所示空间机构为例，柔性连杆-圆柱铰模型为柔性连杆，以圆柱铰1位置处的销轴与轴套为实际的圆柱-圆柱接触作用，圆柱铰2位置处为理想的旋转约束，静摩擦和动摩擦的临界速度[33]分别为vs=1.0 mm/s和vd=1.5 mm/s，计算与对比分析无摩擦和干摩擦下含间隙三维圆柱铰内摩擦作用对系统动态特性的影响。

图16和图17分别为不同摩擦作用下三维圆柱铰的接触点处的切向相对速度和摩擦因数的变化规律。分析可知，含间隙三维圆柱铰内无摩擦和有摩擦时接触点处的切向相对速度的周期变化规律具有相似性，近似为半正弦函数规律，在起始阶段和0.4～0.5 s，连杆le经过竖直Y方向运动，存在较明显的冲击波动变化。摩擦因数较大时，连杆le返回经过竖直Y方向，存在较明显的冲击波动变化。摩擦因数在此区域也存在明显冲击波动变化。在切向相对速度经过零点时摩擦因数按照式(16)规律在动摩擦因数和静摩擦因数之间变化，此时较小摩擦因数下波动变化更为明显，变化时间更长。图18和图19分别为不同摩擦作用下三维圆柱铰的接触点处的法向接触力和摩擦力变化规律。无摩擦时法向接触力的整体变化平缓，而在起始阶段和连杆le经过竖直Y方向附近区域，有摩擦时法向接触力和摩擦力的冲击峰值更大，整体变化规律相似，摩擦因数越大时，冲击峰值更大。图20为不同摩擦作用下圆柱铰2的Z方向的旋转约束反力FZ的变化规律。有摩擦时约束反力的变化规律与无摩擦时具有整体相似性和周期性，幅值更大，冲击波动更频繁。图21和图22分别为不同摩擦作用下三维圆柱铰销轴中心的振动位移和角位移的变化规律。有摩擦时销轴中心的位移变化规律整体上与无摩擦时具有相似性，但位移的振动变化更为频繁，在Y方向平动位移和角位移的振动幅值更大。图23为连杆ce的末端A点的空间轨迹变化规律。有摩擦时，末端点A的运动轨迹的变化范围相似，但变化规律和终点坐标的差异较大，含间隙的三维圆柱铰内摩擦对系统末端的运动学与动力学特性有着重要的影响。

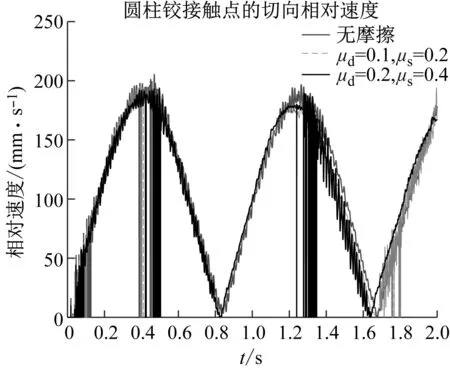
图16 不同摩擦作用下切向相对速度

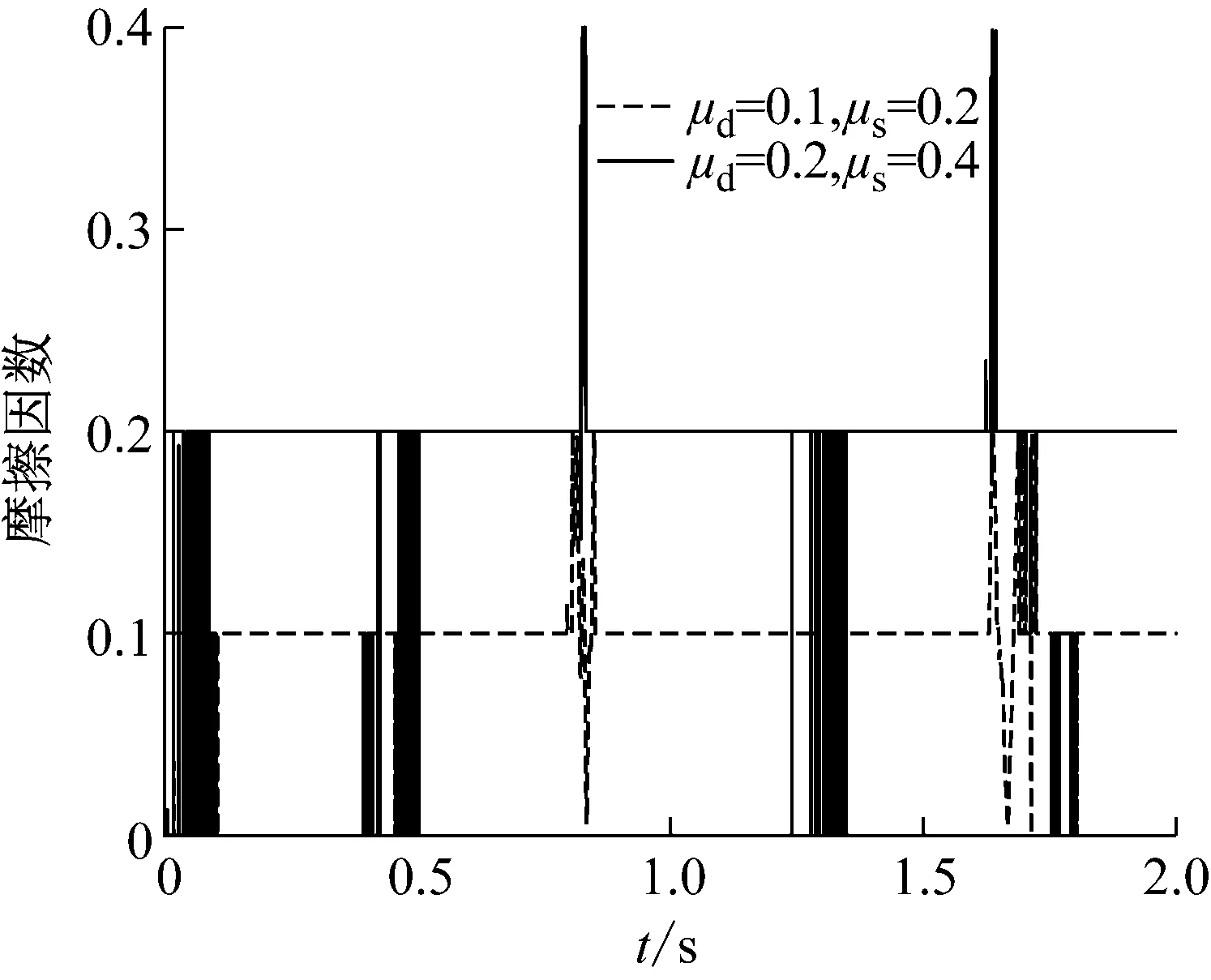
图17 不同摩擦作用下摩擦因数

图18 不同摩擦作用下法向接触力

图19 不同摩擦作用下摩擦力

图20 不同摩擦作用下圆柱铰2的约束反力

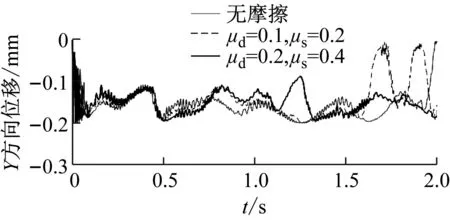
图21 不同摩擦作用下销轴中心的振动位移

4 结 论

关节处的三维圆柱铰的动态性能对高精度空间机〗构系统的动力学特性和运动精度有着至关重要的影响。考虑三维圆柱铰的动态接触关系的空间机构柔性多体动力学模型采用三维圆柱-圆柱线接触方法，能预测持续接触、间隙碰撞状态和摩擦作用，更为真实地模拟空间机构的动态响应特性和运动轨迹。本文仅计算分析单一关节位置处的三维圆柱铰的动力学特性，可以将提出的方法扩展到复杂变工况下高精度、多间隙、多三维圆柱铰-机构系统的空间动力学分析与动态设计。

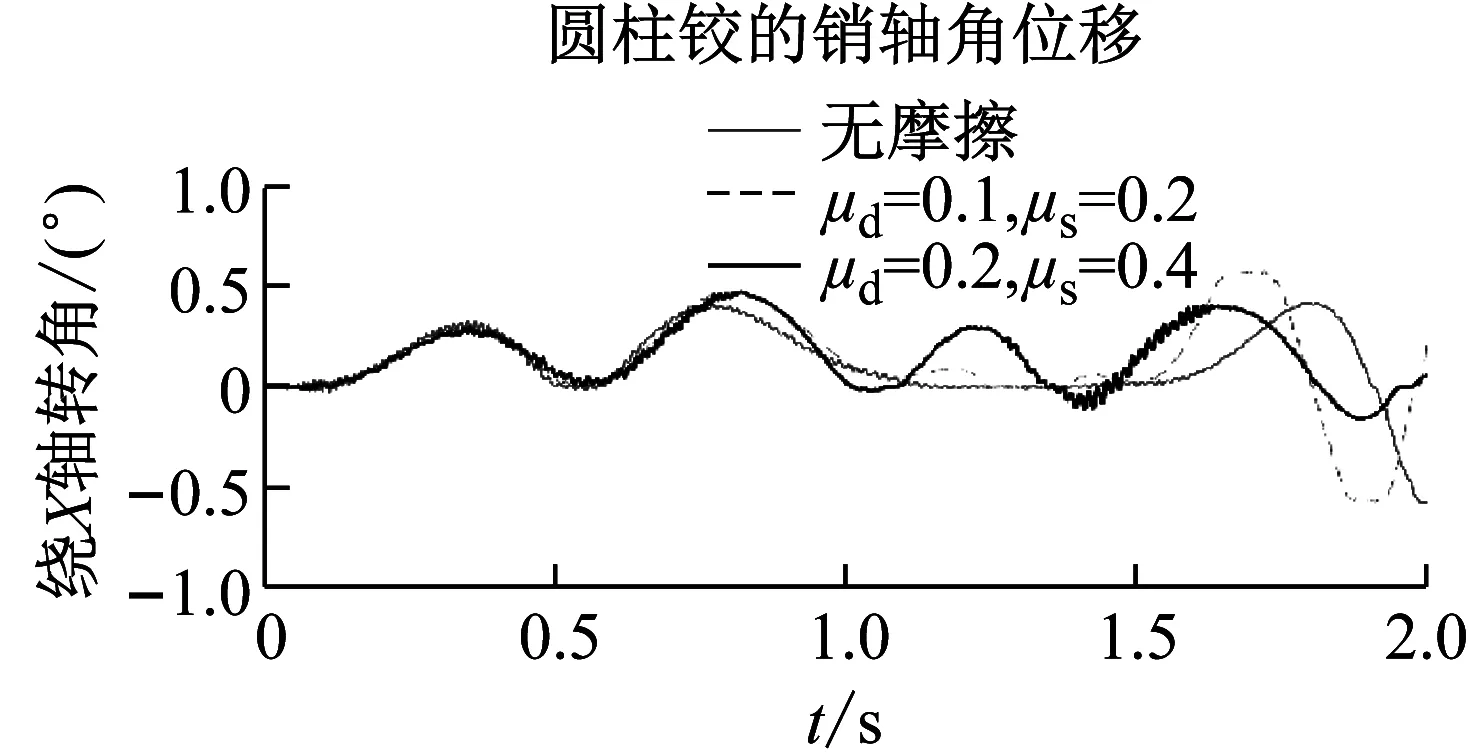
图22 不同摩擦作用下销轴中心的角位移

图23 不同摩擦作用下连杆ce末端A点轨迹

(1) 基于多体动力学方法和刚体有限元方法，采用圆柱-圆柱的线接触方法和切片法，计算圆柱-圆柱的接触变形量和接触力，建立三维圆柱铰的轴销与轴套之间的间隙碰撞作用和三维动态接触关系。计算三维间隙圆柱-圆柱单铰的不同接触状态，验证了接触模型的准确性。采用有限段的等效刚体单元和Timoshenko梁单元，描述柔性连杆的结构弹性变形，提出考虑三维圆柱铰的动态接触关系和间隙碰撞作用的空间机构柔性多体接触动力学方法。

(2) 考虑三维圆柱铰动态接触关系的空间机构模型与理想铰的运动轨迹总体相似。忽略连杆的弹性变形和三维圆柱铰的间隙碰撞作用的理想铰的计算结果与工程实际存在一定的误差。同时考虑连杆的弹性变形和三维圆柱铰的间隙接触碰撞关系，柔性连杆-有间隙圆柱铰模型较为真实地模拟空间机构的动态响应特性。

(3) 仅受重力作用时，无间隙三维圆柱铰的圆柱-圆柱连续接触，无碰撞现象，圆柱铰内的动态接触力与理想铰的约束反力的幅值和变化规律相同。有间隙三维圆柱铰的圆柱-圆柱存在持续接触和间隙碰撞两种典型的动态接触现象。当圆柱-圆柱存在持续接触作用时，动态接触力的幅值及变化规律与理想铰的约束反力相近。当圆柱-圆柱存在间隙碰撞和摩擦作用时，三维圆柱铰内存在较大幅值的碰撞力，且空间机构在下降过程比上升过程出现间隙碰撞作用的更频繁，不同间隙碰撞和摩擦作用对空间机构的系统的动力学特性和运动精度，动态设计和疲劳寿命预测有着重要的影响。