单层和双层足尺度海底管道抗冲击性能分析

谢丽媛, 邵永波, 高旭东

( 西南石油大学 机电工程学院，成都 610500 )

海底管道主要用于海洋中的油气输运，在服役过程中受海浪冲刷而容易产生悬空状态。暴露在海水中的海底管道可能受到重物产生的冲击荷载，如船舶抛锚过程中锚对管道的冲击。冲击载荷会造成管道的弯曲和局部凹陷，严重时会造成管道的破坏。

海底管道是一种钢管构件，目前国内外对钢管抗冲击性能已经做了相关研究。在理论研究方面，Soares等[1]对圆钢管的抗冲击性能进行了研究，提出一种适用于冲击作用下钢管构件的刚塑性分析公式。Jones等[2]提出了一种对管道变形截面进行理想化处理的方法，对圆钢管进行了系统的抗冲击性能分析。Zeinoddini等[3-5]对横向冲击作用下的钢管的抗冲击性能进行了大量的实验研究。目前国内外很多学者使用数值模拟方法对横向冲击作用下的管道抗冲击性能进行研究。杨秀娟等[6-7]采用非线性动态有限元法模拟了海底管道受坠物撞击的过程，求解出了海底管道受坠物撞击时的动力学方程。黄新等[8]发现增大壁厚可以提高抗压强度与承载力。骆吉庆等[9]研究了浅海输气管道坠物碰撞损伤过程中的动力响应规律。杨政龙等[10]研究了深水环境下外界水压对管道碰撞损伤及屈曲失稳的影响，研究表明：落物撞击主要影响管道结构的初始稳定性，同时静水压力会加剧管道的局部凹陷变形。另外，李伟等[11-15]对海底管道抗冲击性能的影响因素进行了研究。针对双层填充管的抗冲击性能，Wang等[16]发现ULCC填充管比空心钢管有更好的抗冲击性能，试件的抗冲击性能和破坏模式由外管和厚度直接决定，同时复合材料层可以有效地限制钢管的局部变形。

针对钢管混凝土的抗冲击性能也有很多学者进行了研究。王宇等[17]研究了双层钢管混凝土组合结构在多次侧向冲击作用下的抗冲击性能，研究发现混凝土层有效限制了结构的凹陷变形。史艳莉等[18]分析了内配圆钢管的圆钢管混凝土构件在横向撞击作用下的动力响应全过程和典型破坏模态，发现提高外钢管的强度和含钢率可以有效地改善该构件的耐撞性能。

虽然国内外很多学者对钢管构件的抗冲击性能进行了研究和分析，但这些研究结果和结论尚不能直接用于海底管道抗冲击性能的评估中，主要原因有两个：①前期对钢管的冲击试验中设计的钢管构件尺寸都较小，与实际中的海底管道足尺度相差较大；②海底管道中除了单层管外，还经常采用双层管，目前尚未对双层管的抗冲击性能进行相关研究。基于上述原因，有必要开展海底管道足尺度试件的抗冲击性能分析，并研究单层管道和双层管道在抗冲击性能上的差异。

1 试验测试及分析

按照渤海海域中实际服役的海底管道设计了4个试件，试件的尺寸和使用的钢材与实际服役的海底管道相同。4个试件中包括3个单层管道(G1，G2和G3)和1个双层管道(G1-D)，双层管道内部有填充物，填充物为聚氨酯弹性体保温材料(SPU)。详细信息如表1和图1中所示。G1-G3是具有不同直径和厚度的单层管道，G1和G1-D的外管完全相同。

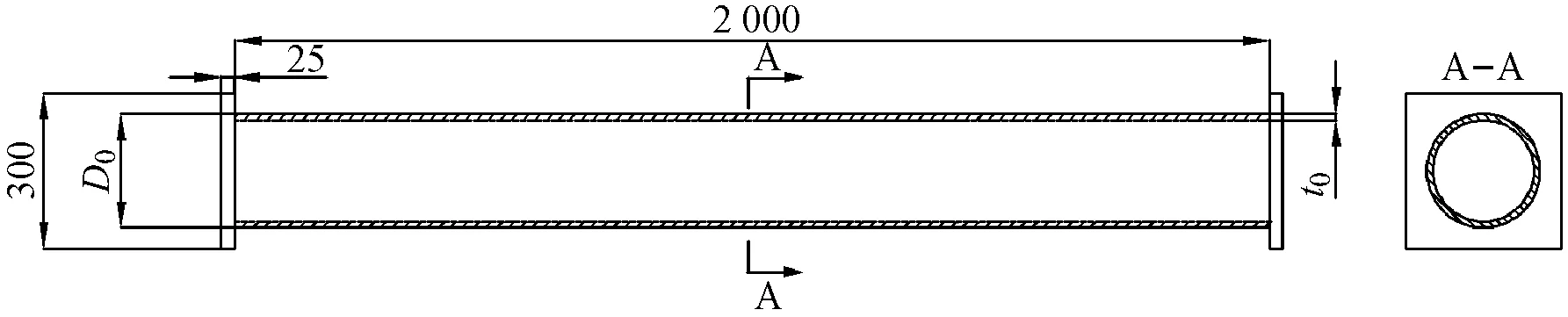
(a) 单层管试件

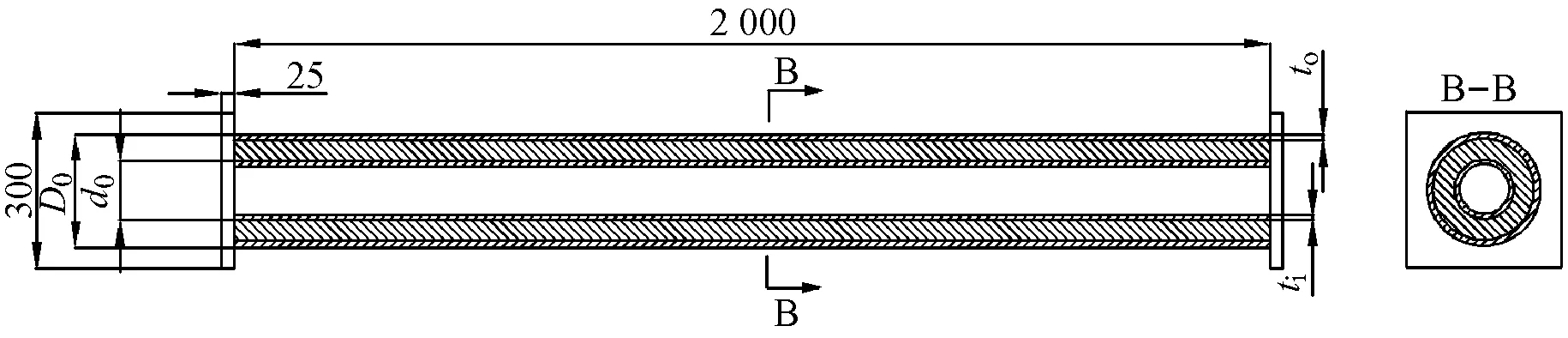
(b) 双层管试件

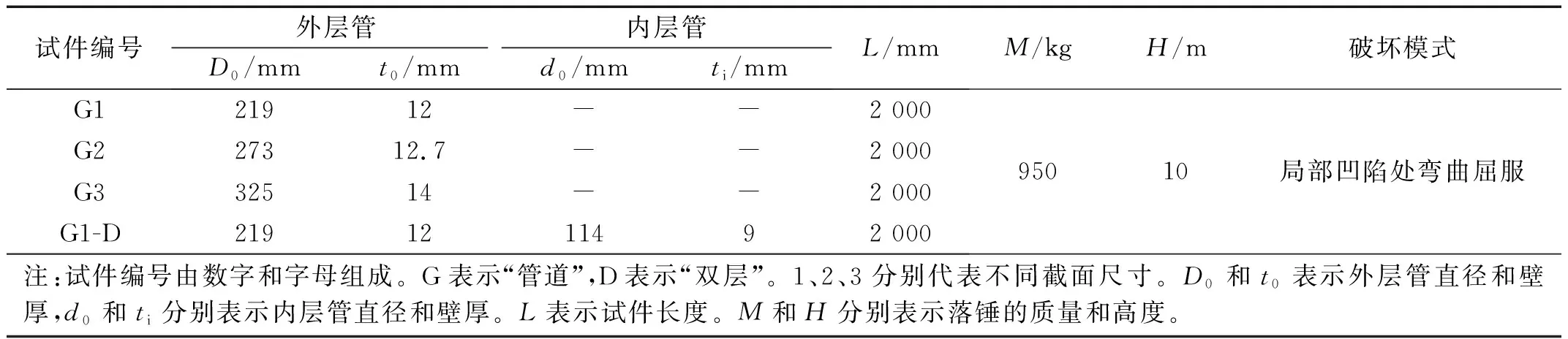
表1 试件尺寸、落锤冲击设置及破坏模式

落锤试验测试之前，首先对管道的材料性能进行测试。通过标准拉伸试件的静力测试，得到了管道材料的弹性模量、屈服强度、断后伸长率、断面收缩率等力学性能测试结果见表2。

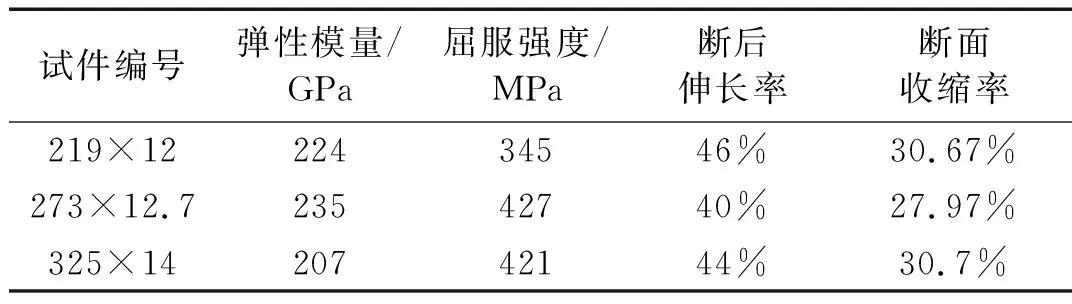
表2 管道材料的力学性能

填充物聚氨酯弹性体(SPU)的力学性能由厂家进行提供，数据见表3。

表3 聚氨酯弹性体(SPU)的力学性能

落锤冲击试验通过超高重型落锤试验机完成，该仪器包括锤头、轨道、提升系统、控制系统及配套夹具等，如图2所示。试件采用渤海胜利油田在役管线，参照API SPEC 5L标准设计了四种受冲击试件，试件尺寸图如图1所示。试验前通过卷扬机将锤头提升到一定高度，确保锤头位置和试件中心对齐后松开落锤，即锤头撞击点始终位于试件的跨中部位。随后落锤在重力作用下沿导轨做自由落体运动，对试件产生撞击。冲击试件管道长度均为2 000 mm，其夹持部位之间的跨度约为1 700 mm。管道水平放置在落锤试验机上，由左右两边的夹具进行固定，一端是固定支撑，另一端为滑动支撑。

落锤试验机配有自动数据采集系统，让落锤自由下落冲击试样，落锤在接近试样前100 mm时经过速度传感器，可计算出落锤的冲击速度及冲击前的加速度，同时给出信号触发高速摄像开始协同拍摄，从而系统自动采集测量数据。

冲击力时程曲线采用压电传感器测量，如图2所示。位移时程曲线由高精度电阻式位移传感器测得，位移传感器分别安装在试件跨中底部U-1和两侧U-2、U-3，如图3所示。应变时程曲线采用BFH120-3AA应变片测量。应变片粘贴位置确定方法：使用有限元分析软件对受动态冲击载荷的海底管道进行模拟，在最大失效位置粘贴应变片。应变片粘贴位置如图3所示：沿试件轴向，应变片分别粘贴在试件中部以及距跨中上、下400 mm处；沿试件环向，每间隔90°粘贴1个应变片，共粘贴10个应变片。为了对不同几何参数和层数的海底管道抗冲击性能进行对比，所有试件加载条件(包括落锤质量M和高度H)均相同，如表1所示。

(a) 试验装置图

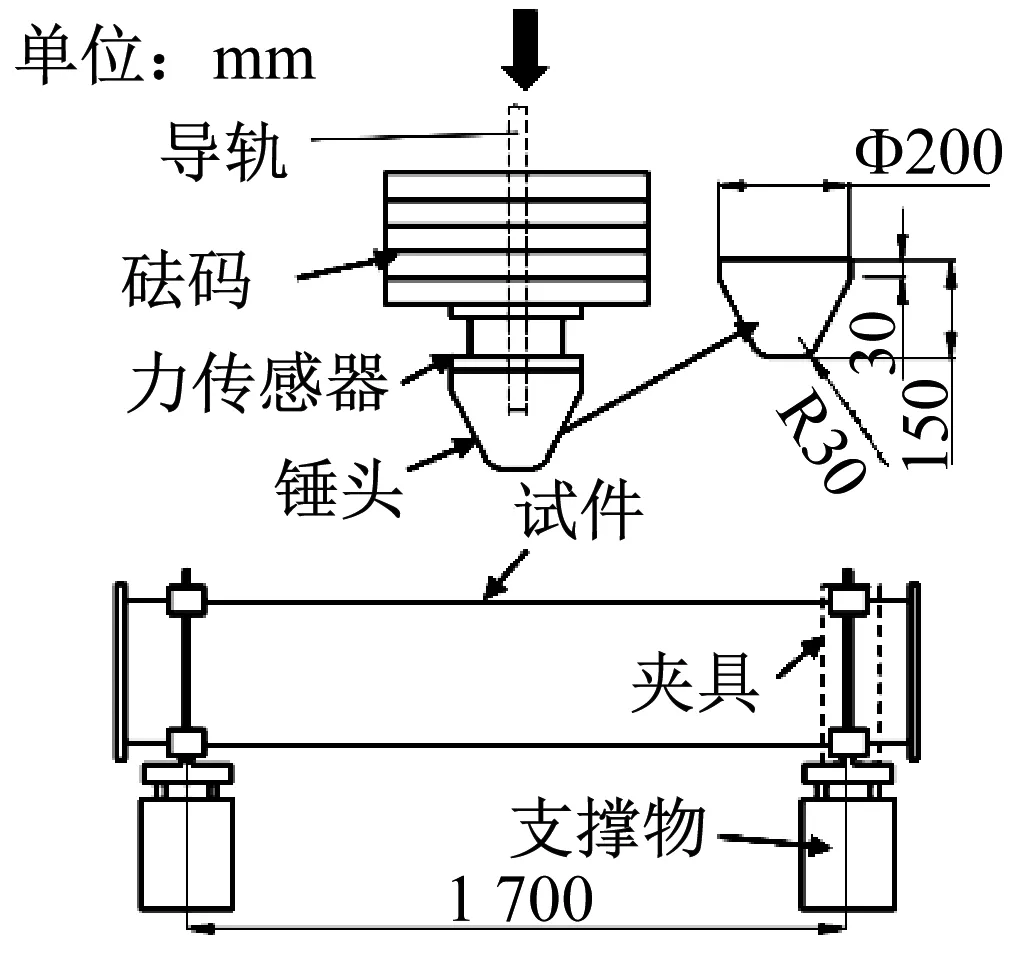
(b) 落锤试验机示意图

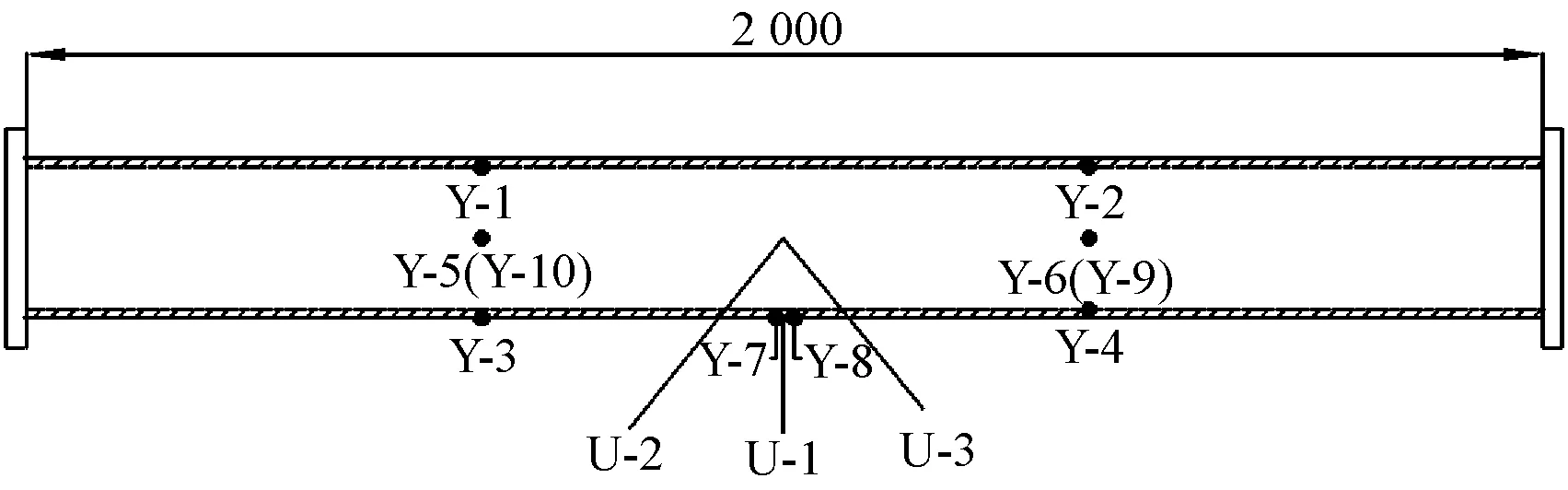
图3 应变片与位移计位置

2 试验结果及分析

2.1 失效过程

试验采用高速摄像机对试件变形进行记录。以G2试件为例，如图4(a)所示，落锤自由落体阶段(0～7 ms)，在这一阶段落锤与试件之间没有发生能量转化，只有落锤将自身的势能转化为动能，产生初始速度。落锤与试件初始接触瞬间(7 ms)，如图4(b)所示，冲击力迅速增大，跨中上表面位移开始增加，出现局部凹陷；跨中下表面位移为0，没有产生整体弯曲变形。随后(7～32 ms)，试件的局部凹陷变形不断扩大，管道弯曲变形逐渐加深，同时试件上白漆逐渐脱落，如图4(c)所示。32 ms时，试件的跨中上下表面位移达到最大，即试件的局部凹陷变形和整体弯曲变形达到最大值，如图4(d)所示。随后(32～42 ms)，试件弹性部分恢复，落锤与试件同步回弹，试件跨中上下表面位移逐渐减小，即局部凹陷变形和整体弯曲变形逐渐减小，如图4(e)所示。42 ms后，如图4(f)所示，位移回弹结束，落锤与试件分离，第一次冲击过程结束。

(a) 0～7 ms

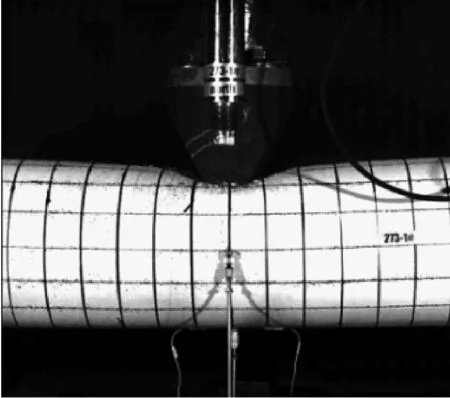
(c) 7～32 ms

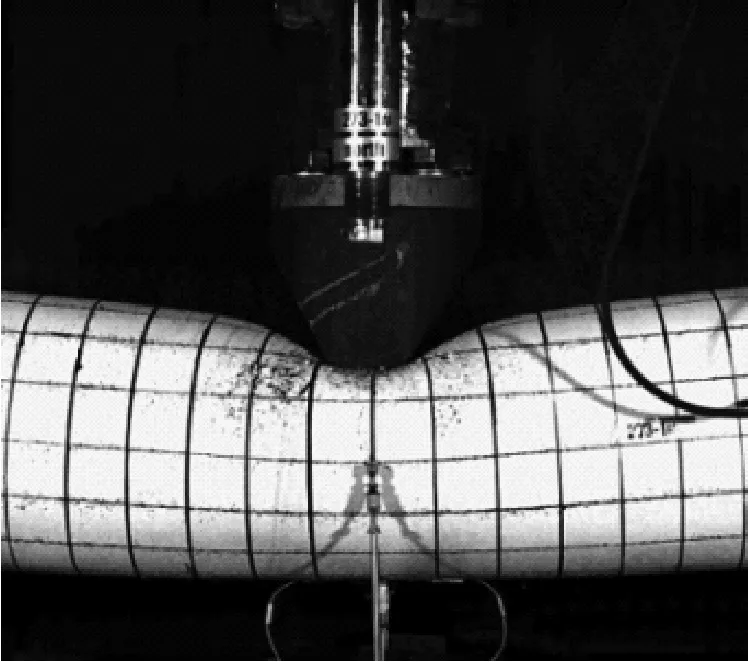
(d) 32 ms

(e) 32～42 ms

(f) 42 ms

(g) 冲击物与凹痕形状对比

试验结果表明，所有试件在受到横向冲击载荷时的破坏形态相似，都是局部凹陷处弯曲屈服。这种破坏模式由冲击接触部位的局部凹陷变形和管道的整体弯曲变形共同形成。如图4(g)所示，试件局部凹陷的凹痕形状与冲击物的形状保持一致，这与文献[15]得出的结论一致，故不再对冲击物形状因素进行分析。

2.2 冲击力时程曲线

图5(a)为单层管道的冲击力时程曲线。冲击力时程曲线可以分为四个阶段：初始阶段、振动阶段，稳定阶段和卸载阶段。以G1试件为例，在初始阶段(AB段)主要特征是冲击力波动较大，在落锤与试件接触瞬间，由于惯性效应产生第一个冲击力尖峰。由于落锤与试件的接触时间非常小，在图中表现为冲击力突然达到最大值。在这一阶段弹性变形为主要变形形式，冲击力时程曲线近似呈现线性增长。振动阶段(BC段)的特征是冲击力产生剧烈振动，由于试件受到横向冲击时会产生轴向收缩，使边界约束产生变化，造成冲击力迅速下降，轴向收缩至一定程度后，冲击力继续增加至冲击力峰值，这一阶段冲击力随时间的增长速度明显不如第一阶段。稳定阶段(CD段)的特征是冲击力变化很小，近似于平台阶段。卸载阶段(DE段)的特征是冲击力迅速降，此时试件弹性逐渐恢复，冲击力减小。当落锤与试件速度降为0时，冲击力卸载为0，冲击过程基本结束。

海底管道在受到横向冲击载荷作用时其冲击力时程曲线都大致经历了初始阶段、振动阶段、稳定阶段和卸载阶段，曲线的变化趋势大致相同。试件G1最大冲击力为578 kN，受冲击时间为53 ms；试件G2最大冲击力为934 kN，受冲击时间为27 ms；试件G3最大冲击力为938 kN，受冲击时间为25 ms。数据表明，随试件径厚比增大，试件的最大冲击力增大，受冲击时间减小，试件的抗冲击性能增大。

图5(b)为双层管道冲击力时程曲线。双层管G1-D的最大冲击力为774 kN，受冲击时间为38 ms。冲击时程曲线趋势与单层管道类似。当双层管受到横向冲击载荷时，落锤首先与外管发生冲击，产生第一个冲击力峰值(F点)。当局部凹陷到达一定值后，落锤与试件内管接触，产生第二个冲击力峰值(G点)。冲击力峰值G点要远大于F点。

图5(c)为单双层管道冲击力时程曲线对比图。与单层管相比，双层管冲击力峰值升高，受冲击时间减小。这是由于内层管使试件刚度增加，导致冲击力峰值增大，受冲击时间减小，抗冲击性能显著提高。

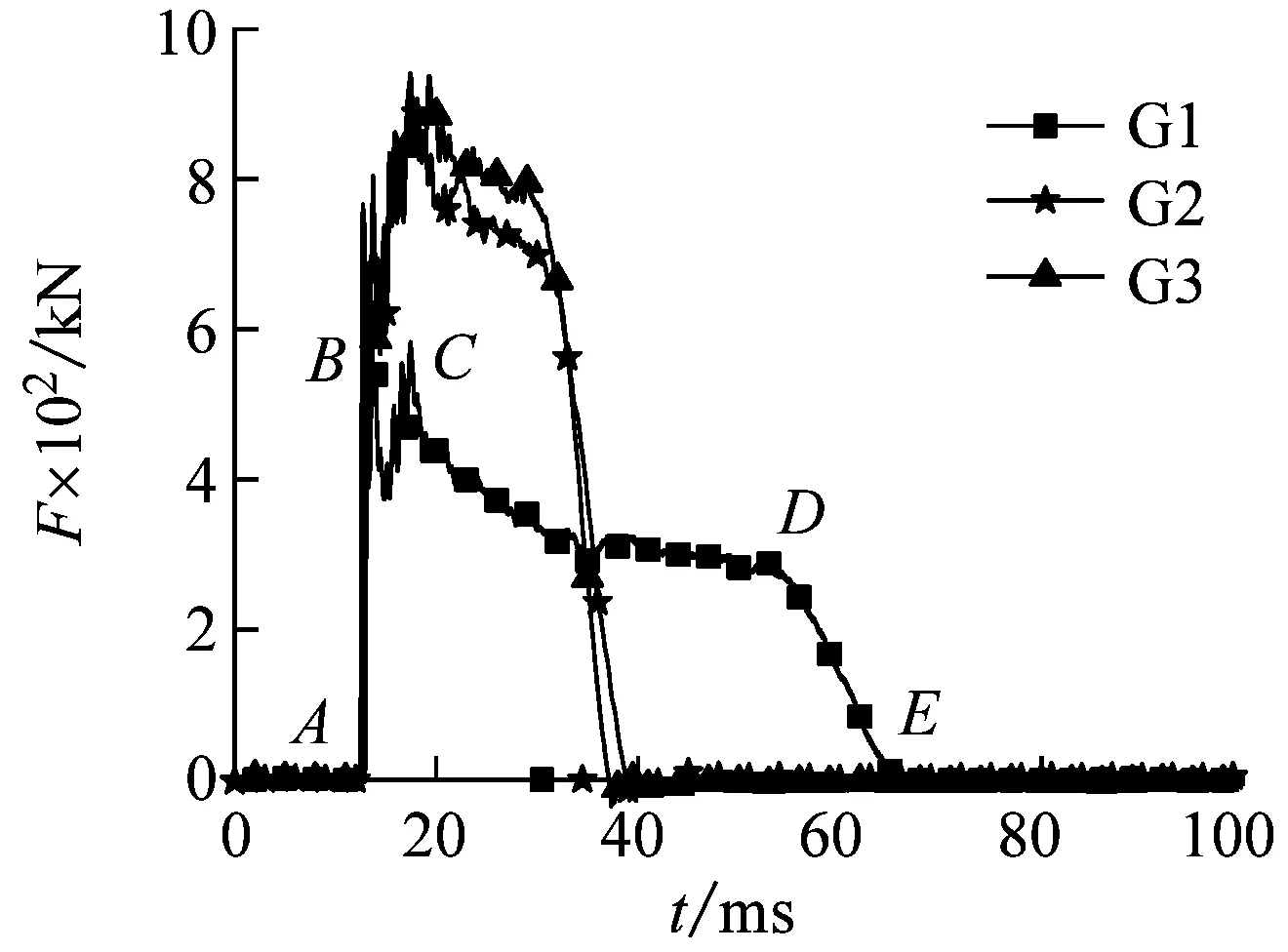
(a) 单层管道冲击力时程曲线

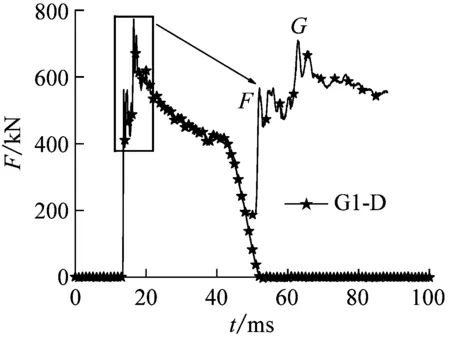
(b) 双层管道冲击力时程曲线

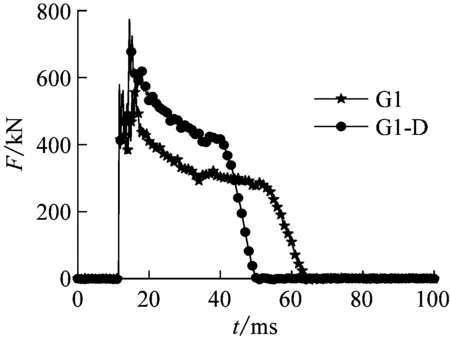
(c) 单双层管道冲击力时程曲线对比

2.3 位移时程曲线

图6(a)和6(b)为单层管道的跨中下表面位移时程曲线(数据由位移计U-1测得)和侧向位移时程曲线(由位移计U-2和U-3检测结果取平均值测得)。可以发现，五条曲线变化趋势基本一致，都经历了迅速增长阶段、回弹阶段、稳定阶段。以G1试件跨中下表面位移为例，在落锤与管道接触瞬间，试件的跨中下表面位移近似呈现线性增长趋势，试件从零增长直至试件变形达到最大158 mm，随后试件弹性部分恢复，落锤与管道进行同步回弹，位移减小。由于管道发生了塑性变形，受冲击结束后试件不可能恢复原状，而是保持在一定值，即试件的跨中下表面残余变形142 mm。值得注意的是，由于试件G3跨中底部位移计U-1脱落，故未测得G3试件跨中底部位移。

单双层管道时程曲线对比如图6(c)和6(d)所示。双层管道与单层管道位移时程曲线类似。试件在冲击初期时，单层管与双层管的局部凹陷与整体弯曲变形同步增加。当位移增大到一定程度时，内层管阻止外层管进一步产生变形，因此双层管受到冲击时产生的位移较小，抗冲击性能更强。

图6(e)为双层管道的冲击力-位移时程曲线。很明显可以看出，落锤冲击双层管时产生了两个冲击力峰值点(A和B)。A和B分别是落锤冲击外层管和内层管产生的冲击力峰值点，它们之间的位移是外层管的壁厚12 mm。

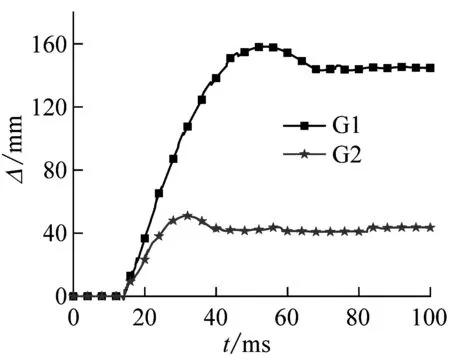
(a) 单层管道跨中下表面位移时程曲线

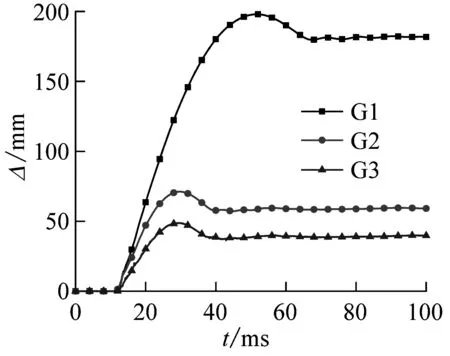
(b) 单层管道侧向位移时程曲线

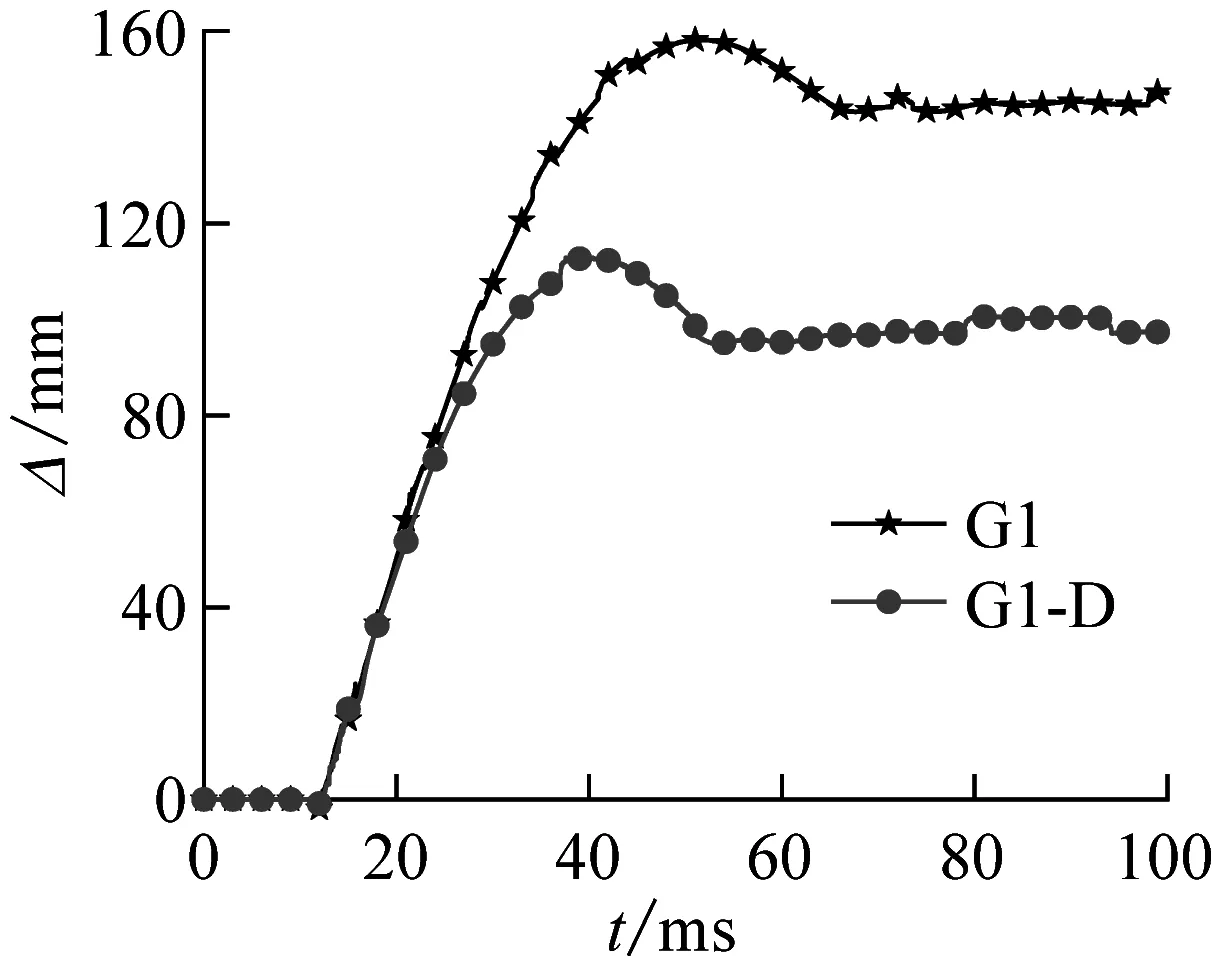
(c) 单双层管道跨中下表面位移时程曲线对比

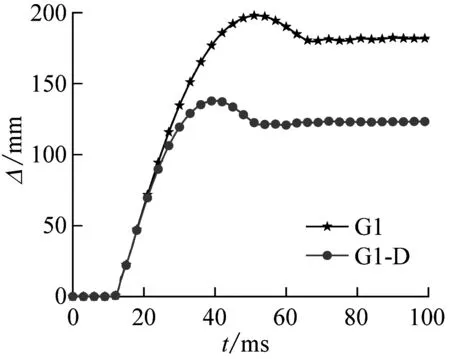
(d) 单双层管道侧向位移时程曲线对比

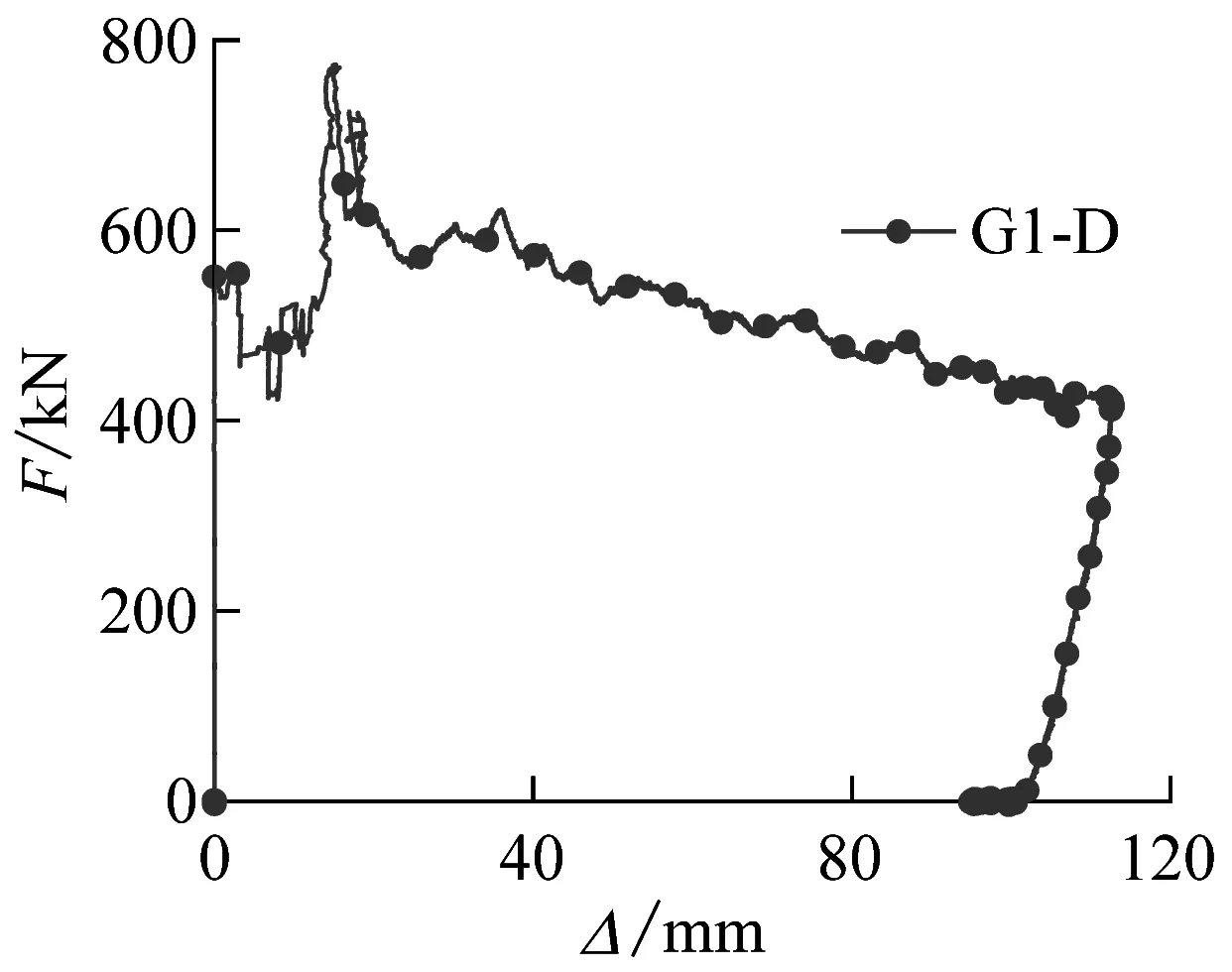
(e) 冲击力-跨中底部位移曲线

2.4 应变时程曲线

钢管表面应变时程曲线如图7所示，图中应变受拉为正，受压为负。值得指出的是由于试件部分位置产生了很大的变形，导致该位置应变片失效，如G1试件编号为Y-7的应变片，G2试件编号为Y-8的应变片，G3试件编号为Y-1的应变片以及G1-D试件编号为Y-7、Y-8的应变片。各测点的变形几乎同时发生，说明试件在瞬间受到很大的冲击能量，变形在很短时间内达到极限，没有明显的传递过程。应变从0迅速增至应变峰值，之后弹性变形部分恢复导致应变减小，由于所有测点的应变都超过了屈服应变，所以受冲击结束后应变不会恢复为0，而是保持一定值，即为残余应变。另外，观察试件底部位移发现应变片Y-3和Y-4达到一定变形程度后会出现平台段，随后试件与落锤分离，应变减小至残余应变。随试件径厚比增加，平台段数值升高，持续时间减小。

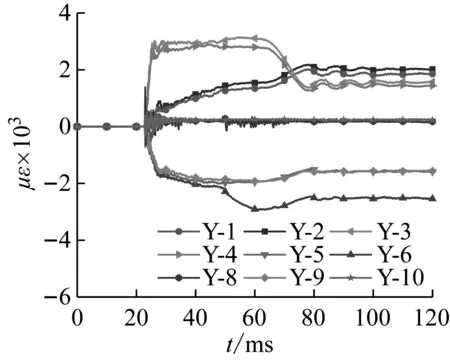
(a) 试件G1

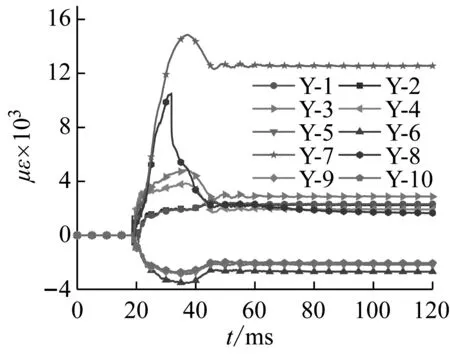
(b) 试件G2

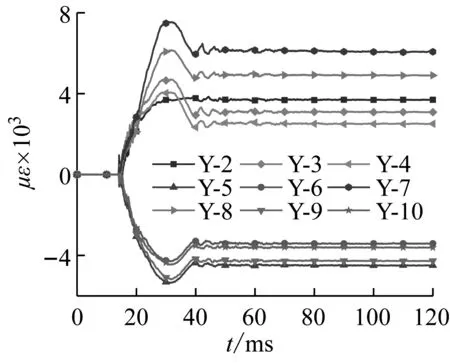
(c) 试件G3

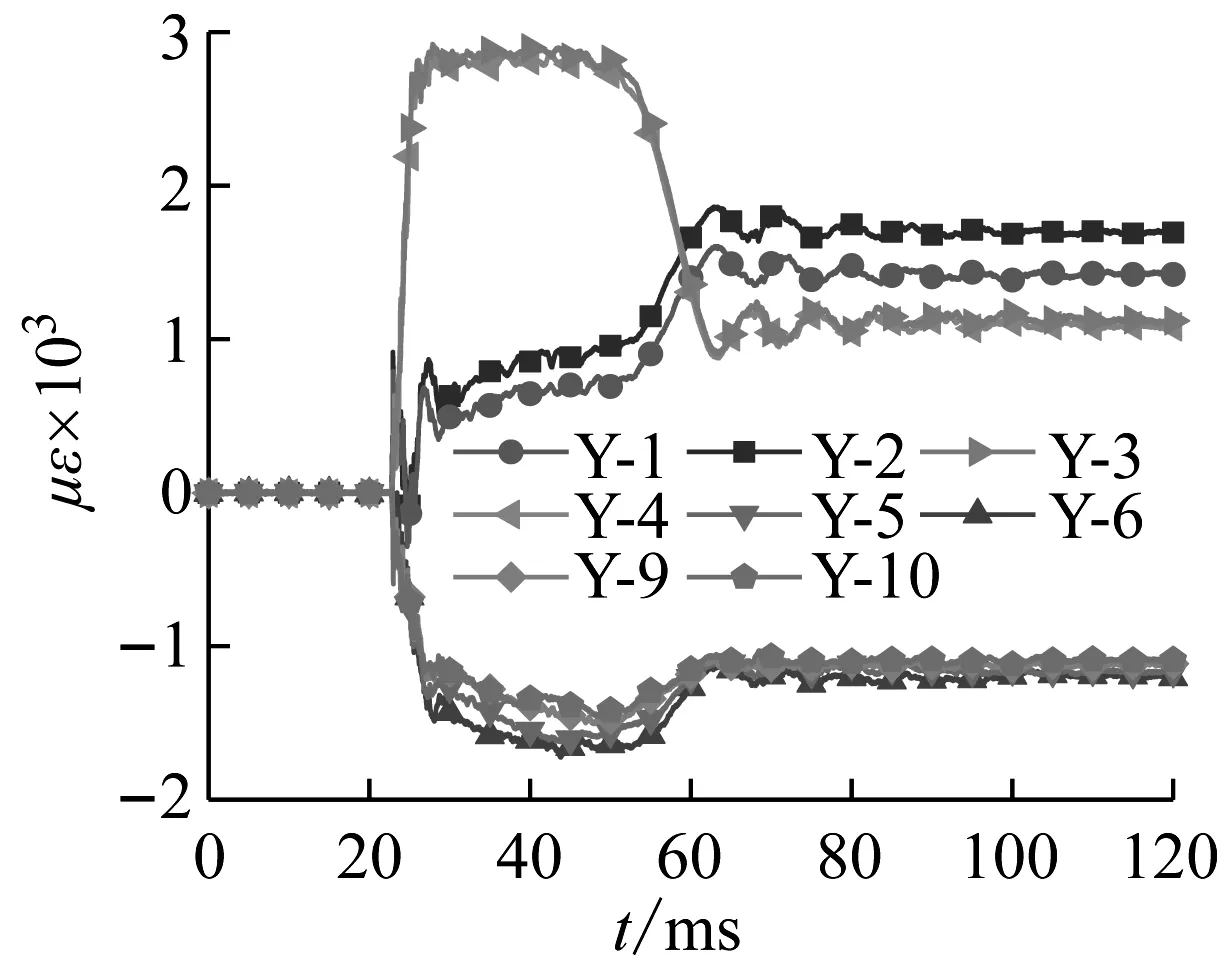
(d) 试件G1-D

应变片Y-1和Y-2测量的是试件上表面应变值，该应变由局部凹陷变形和整体弯曲变形产生，由于局部凹陷的影响使该部位由压应变转变为拉应变。若不考虑测量误差的影响，Y-1和Y-2应变大小不相等可能是由于冲击偏心造成的。Y-5和Y-6应变片测量的是试件下表面的应变值，该应变由整体弯曲变形产生。观察应变时程曲线发现，Y-5和Y-6应变片的应变监测结果大于其他测点的应变，即试件承受动态冲击荷载时跨中下表面在变形最大。

3 有限元分析

3.1 有限元模型建立

利用ABAQUS有限元分析软件，建立了落锤冲击管道的有限元分析模型。有限元模型的示意图如图8所示。由于试验时落锤可以看做是不可发生变形的物体，故可将落锤设置为刚体，并简化到参考点上，在参考点上利用速度场定义初始冲击速度。网格密度的大小影响有限元模型计算的精确度。一般网格密度越大，模型计算的结果就会越接近于真实值，但网格密度过密则会使计算耗时增大。因此要确定合适的网格密度。对受冲击部位的网格进行加密，通过试算确定网格密度，控制网格数量。沙漏效应对模型计算结果的准确度影响很大。伪应变能除以内能是检查沙漏效应的重要指标。当比值较大时，沙漏变形耗散的能量就会很大，导致模拟中能量不守恒。有限元网格划分结果如图8所示，考虑计算效率和精度，受冲击部位网格最小单元尺寸为15，远离冲击部位的网格最小单元尺寸为30，在受冲击部位和远离冲击部位之间采用过渡网格，共60 592个单元和77 179个节点。锤头和试件接触类型采用动态面-面接触，可以很好地滑移接触问题，同时可以输出接触力。在锤头与试件接触时，考虑到二者发生摩擦时的相互作用，取摩擦因数为0.15。其余接触部位采用动态通用接触。

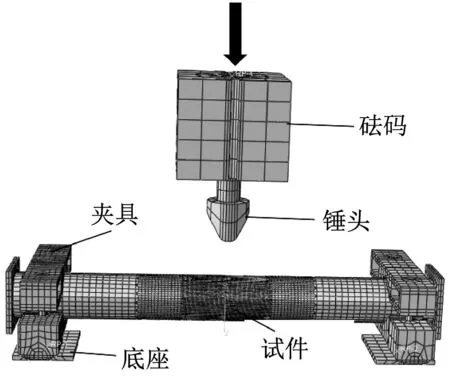
图8 海底管道有限元模型

钢是一种典型的应变速率相关的材料，通常在高速冲击的数值分析中要考虑应变率效应。目前国内外学者主要通过建立动态屈服强度增大系数的表达式来考虑钢的应变率影响。最常用的是由Symonds提出动态屈服强度函数，表达式为

(1)

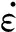
钢的应变率模型采用c-s模型，应变率参数参考文献[19]取值，即D取40.4，n取5。钢的其他材料参数取值使用材料材性分析试验的数据。另外，值得注意的是，聚氨酯弹性体抗冲击性能差，吸能低。因此，在数值模拟中不需要考虑填充材料对抗冲击性能的影响。

3.2 有限元模型验证

图9和图10给出了单双层管受到冲击后的有限元模拟结果与试验结果对比图。试件受到横向冲击后，受冲击部位产生局部凹陷，随后向周围扩展，同时管道整体产生弯曲变形。随试件径厚比减小，局部凹陷变形和整体弯曲变形更加明显，这是由于试件径厚比减小使抗弯刚度增大。与同外径单层管道G1相比，双层管道试件G1-D整体弯曲变形和局部凹陷变形均降低。原因在于在受到一定冲击力后，内层管抑制了管道继续发生变形，导致双层管道抗冲击能力更强。数据表明，有限元软件结果与试验结果基本吻合，因此有限元可以有效地分析管道横向冲击作用下的失效模式。

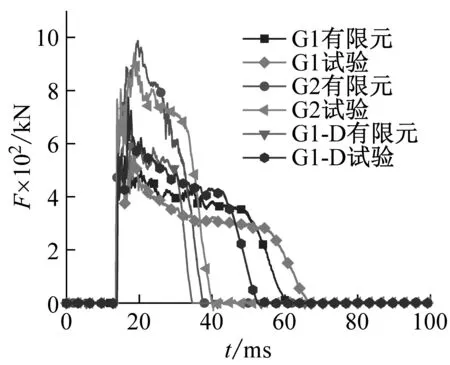
为进一步验证有限元模型的正确性，图11给出了单双层管道抗冲击性能指标的对比图，包括冲击力时程曲线、跨中下表面位移时程曲线、侧向位移时程曲线。在图11(a)冲击力时程曲线可以看到，有限元模拟结果与试验结果曲线趋势基本类似，都经历了初始、振动、稳定和卸载阶段。在卸载阶段，有限元模拟结果与试验结果产生偏差，原因可能是在试验时边界条件具有不稳定性，在落锤冲击管道的瞬间，管道除了发生凹陷变形和弯曲变形以外，还会产生轴向收缩，很难保证受到冲击后的试件依然保持原有的边界条件，这样试件的边界约束就会发生变化，而有限元模拟时能够保证边界条件的稳定性，边界对管道的约束不会发生变化。

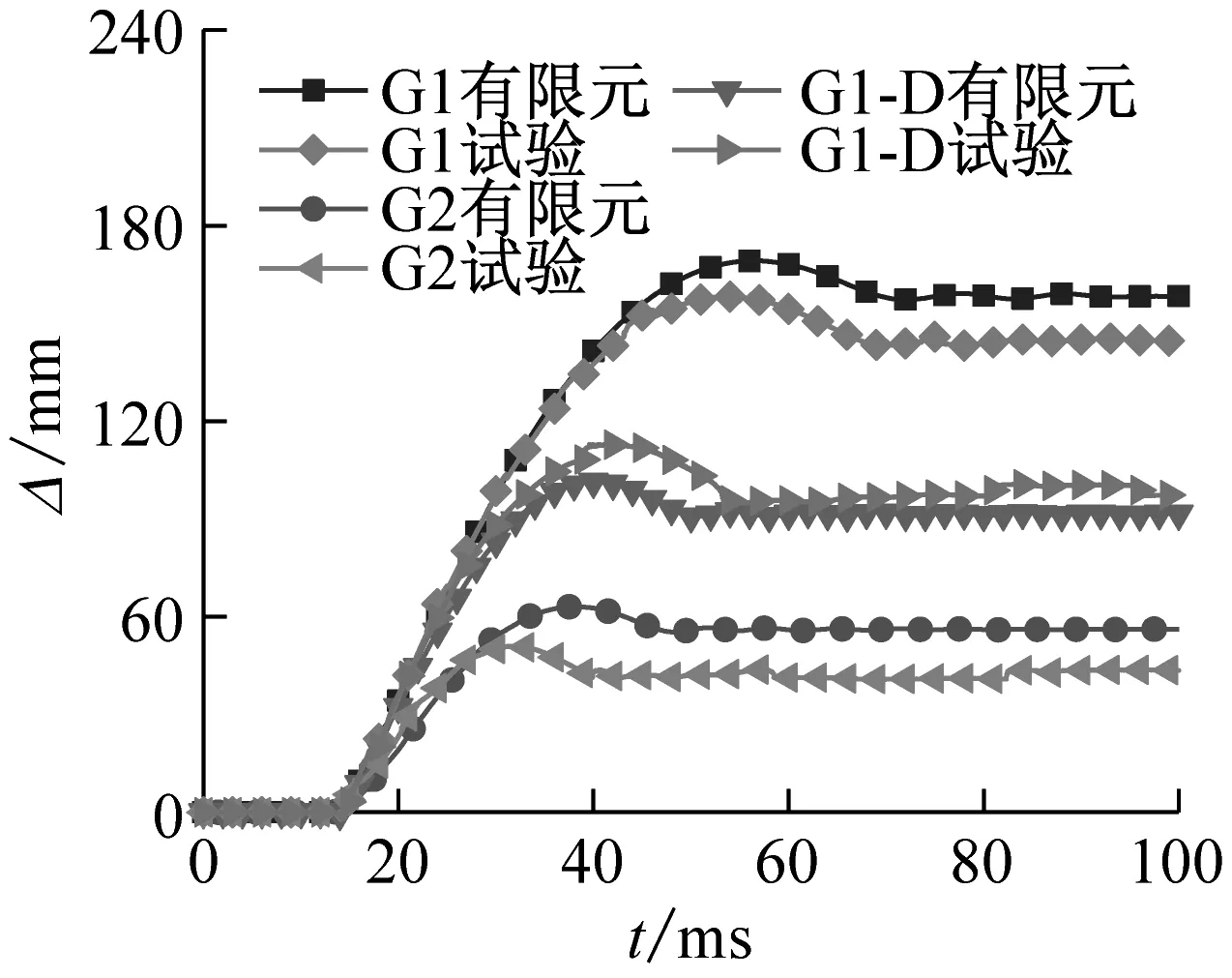
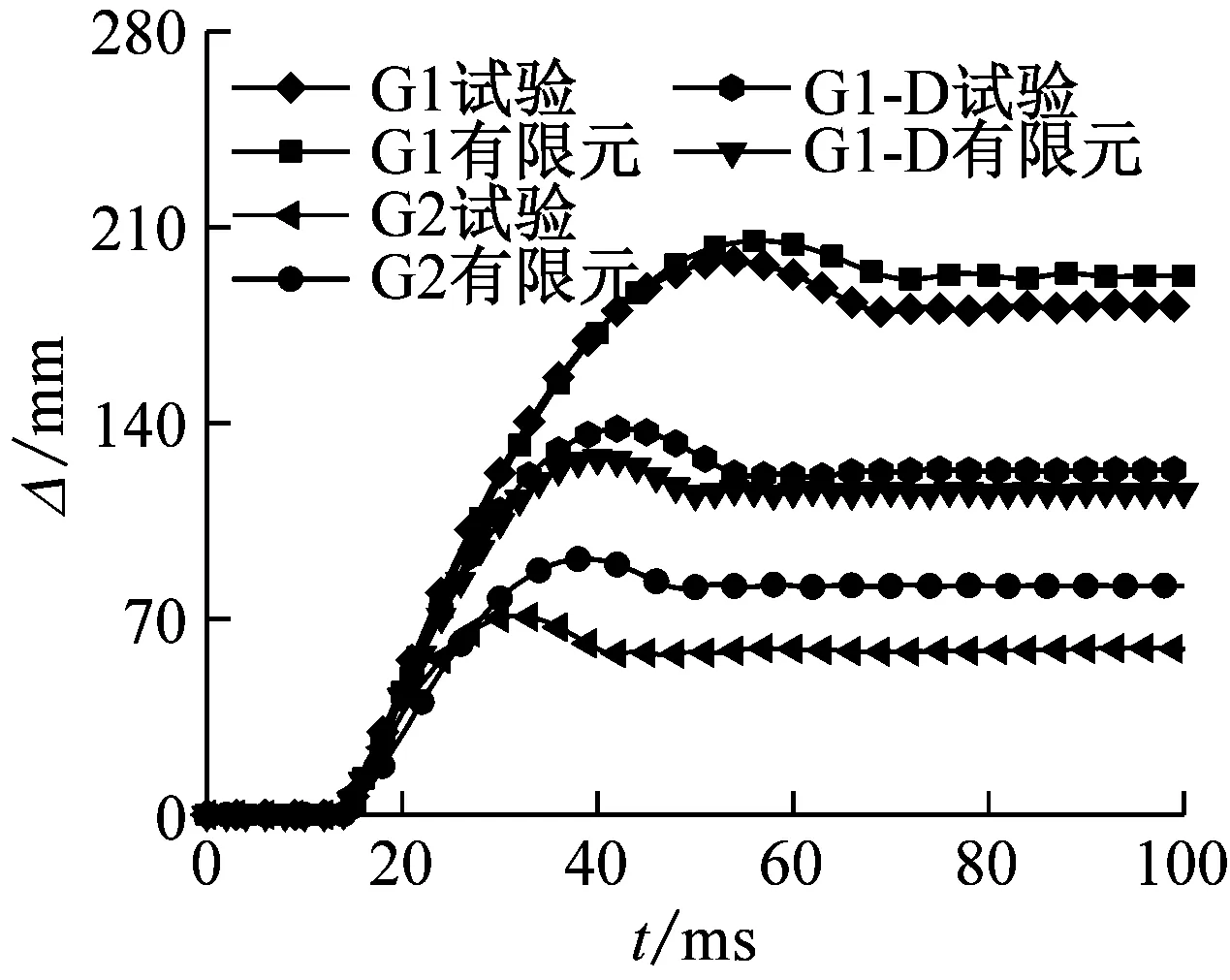
图11(b)和(c)是试件有限元模拟与试验结果的位移时程曲线对比图。有限元模拟结果与试验结果发展趋势基本一致，即试件在横向冲击力作用下，底部位移达到最大值，随后试件开始回弹，直至压头与试件分离。表4列出了有限元模拟结果与试验结果，结果表明所提出的有限元模型可以对试验结果提供合理的预测，值得说明的是，由于试件G3跨中底部位移计脱落，故未测得G3试件的整体弯曲变形。

(a) G1试件有限元结果

(b) G1试件试验结果

(c) G2试件有限元结果

(d) G2试件试验结果

(e) G3试件有限元结果

(f) G3试件试验结果

(a) G1-D试件有限元结果及剖面图

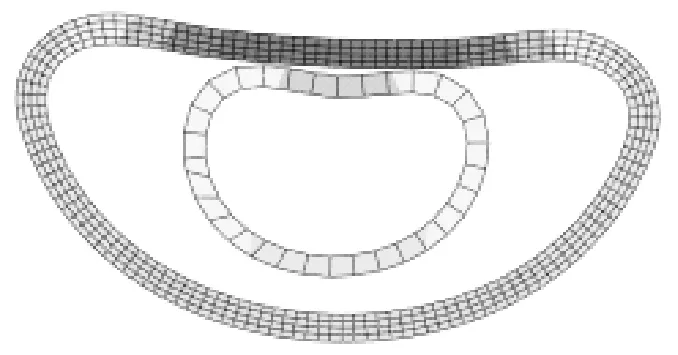
(b) G1-D试件剖面图

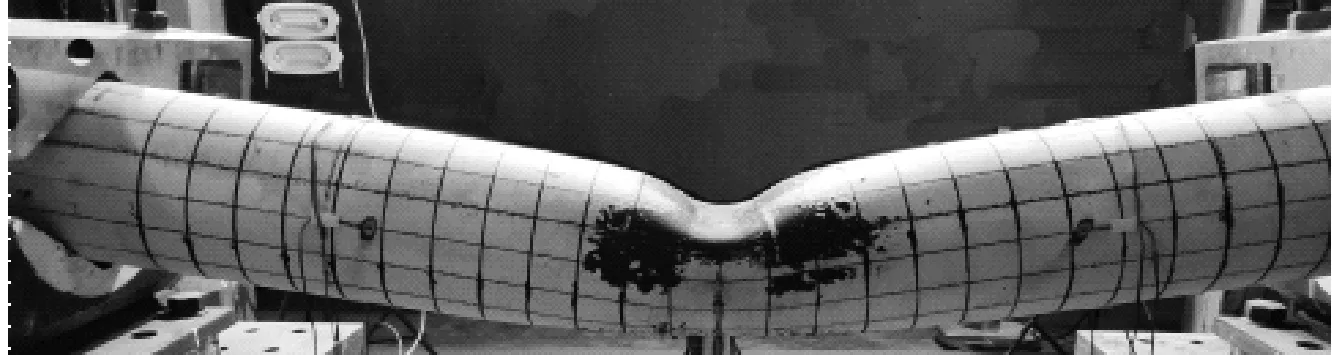
(c) G1-D试件试验结果

(a) 冲击力时程曲线

(b) 跨中下表面位移时程曲线

(c) 侧向位移时程曲线

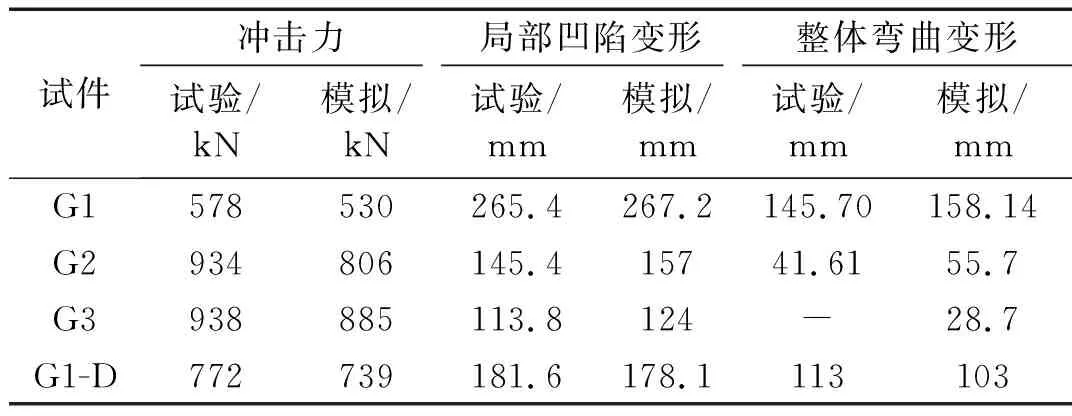
表4 有限元模型与试验结果汇总

4 管道抗冲击性能参数分析

管道抗冲击性能受很多参数影响，选取G1试件和G1-D试件为研究对象对单层和双层管道进行参数分析。表5显示了G1试件参数分析研究的方案，G1-D参数分析方案与G1试件一致。在研究单一参数对试件抗冲击性能影响时，保证其他因素的绝对一致性，本研究对冲击高度、屈服强度、径厚比、长径比四个方面进行分析。对试件的变形特征从最大冲击力、最大跨中变形、残余跨中变形、最大跨中上表面变形、残余跨中上表面变形以及局部变形等方面来进行分析。

4.1 冲击高度影响

为获得冲击高度对抗冲击性能的影响，将冲击高度H改变为9 m、10 m、11 m、12 m、13 m、14 m、15 m。有限元模型中可通过改变冲击速度来模拟不同的冲击高度。落锤对试件施加横向冲击载荷之前做自由落体运动，则落锤与试件接触的初始速度分别取13.28 m/s，14 m/s，14.68 m/s，15.34 m/s，15.96 m/s，16.56 m/s，17.14 m/s。图12显示了单双层管道试件的最大冲击力Fm、最大跨中位移Δmx、跨中残余变形Δrx、最大跨中上表面变形Δms、残余跨中上表面变形Δrs和局部残余变形δr都随冲击高度的变化趋势。显然，当冲击高度增加时，Fm、Δmx、Δrx、Δms、Δrs以及δr均随冲击高度增大。试件的整体弯曲变形和局部凹陷变形随高度增加呈现线性增长趋势，原因在于冲击高度增加使冲击能量增大，从而在其他条件不发生改变时，试件受到的最大冲击力和变形都会增大。对比单双层管道冲击力和位移曲线发现，双层管道的最大冲击力大于单层管道，位移小于单层管道。这是由于双层管道受到一定冲击后，内管产生作用，阻止管道位移进一步增加。

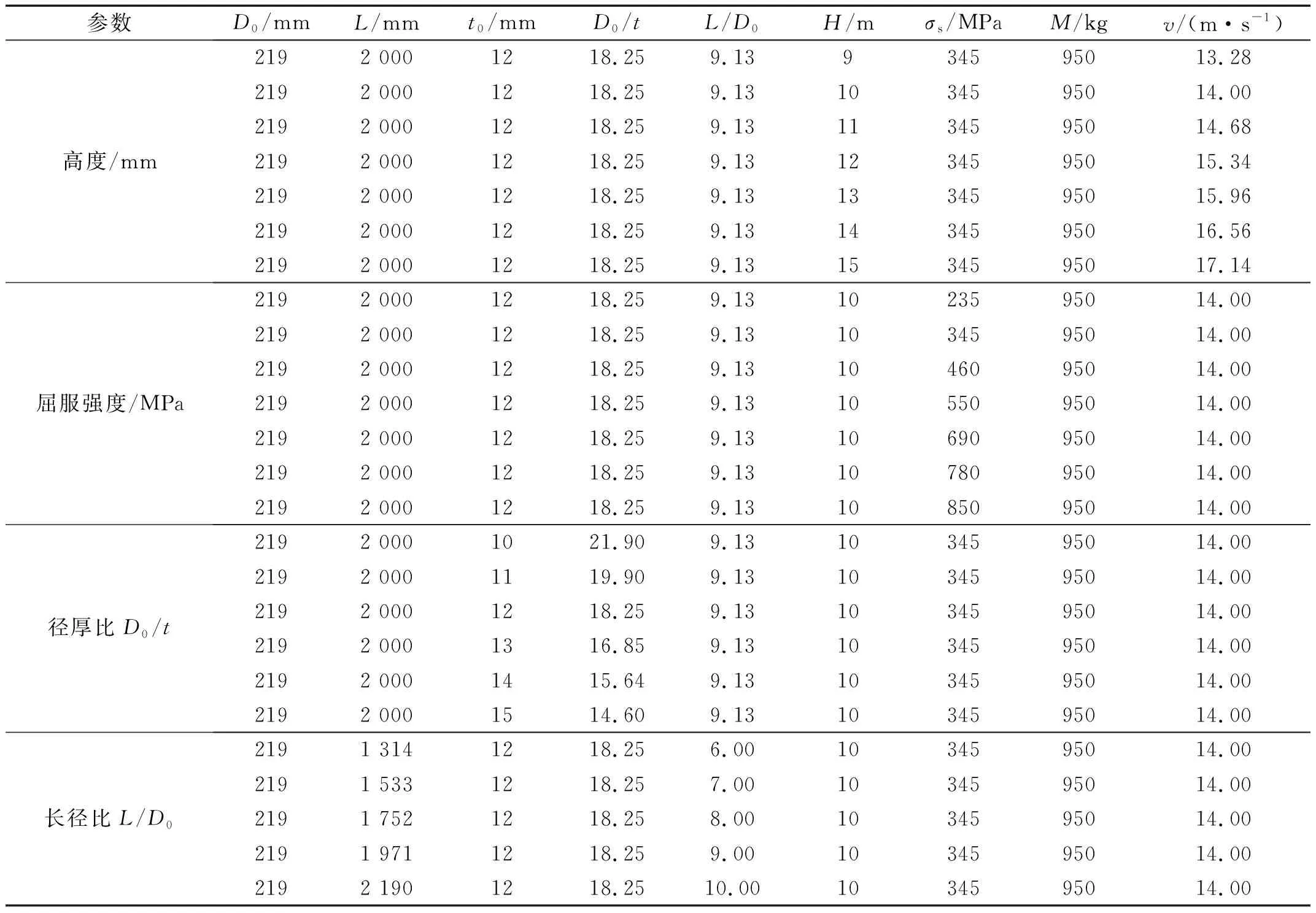
表5 G1试件参数分析表

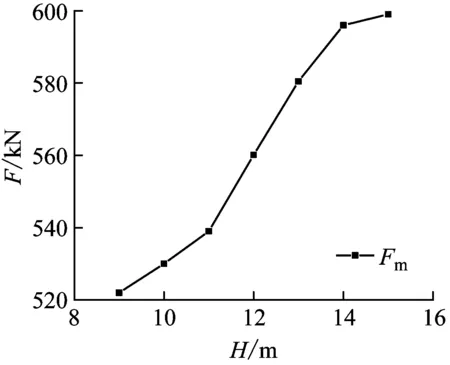
(a) G1冲击力

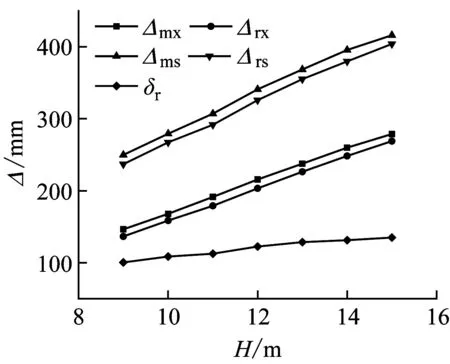
(b) G1跨中位移

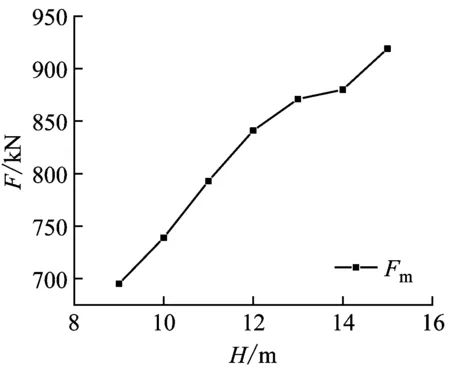
(c) G1-D冲击力

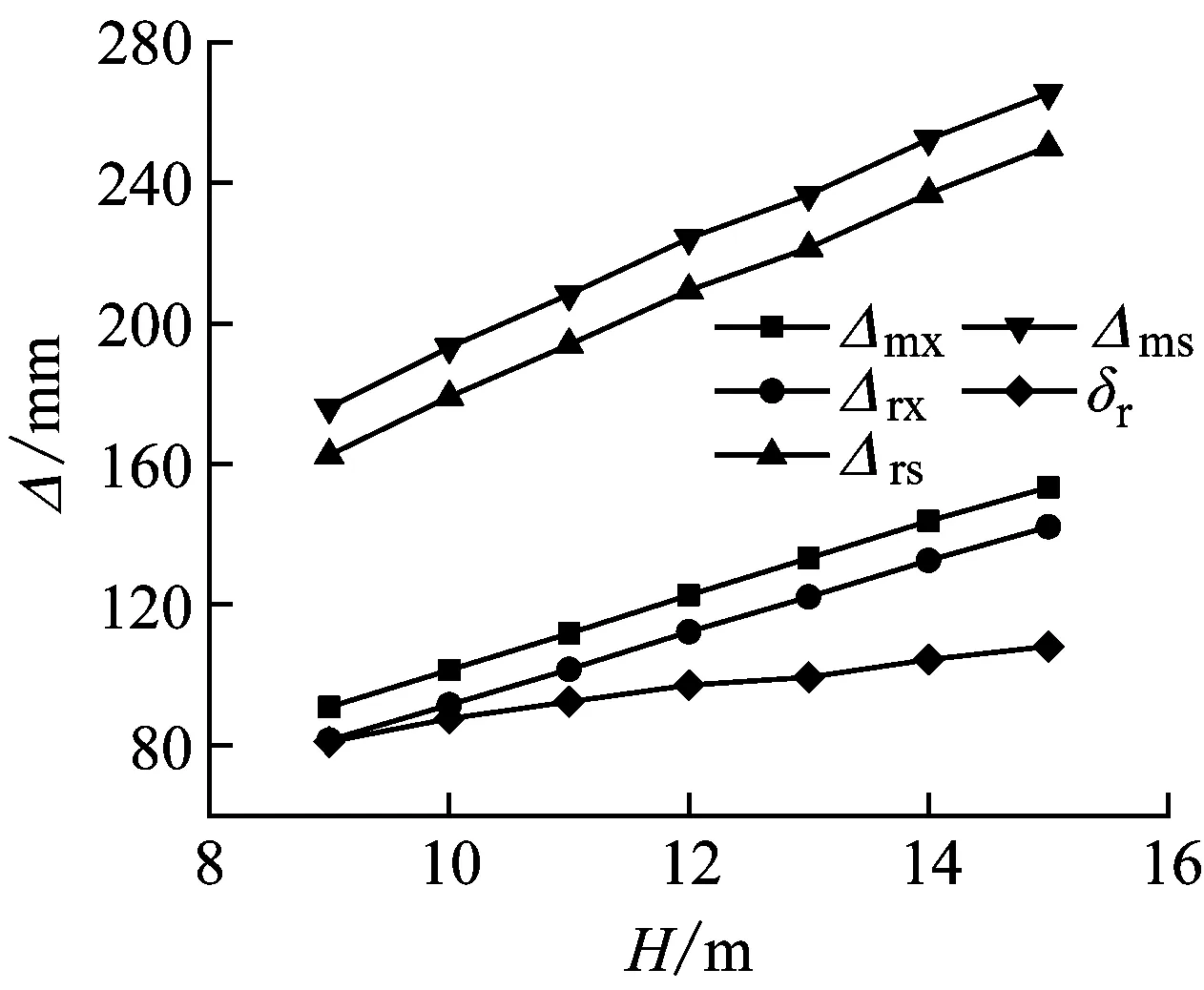
(d) G1-D跨中位移

4.2 屈服强度影响

图13显示了不同屈服应力σs对单双层试件抗冲击性能的影响，屈服应力分别取235 MPa，345 MPa，460 MPa，550 MPa，690 MPa，780 MPa，850 MPa。结果表明：Fm随屈服强度的提高不断增大，这是由于屈服强度增大，试件屈服时荷载提高，从而提高了最大冲击力。Δmx、Δrx、Δms、Δrs以及δr都随屈服强度的提高不断减小。如图13(a～b)所示，当屈服强度从235 MPa增大到550 MPa，即屈服应力增大了315 MPa时，试件的整体弯曲变形降低了138.201 mm，δr降低了46.85 mm；当屈服强度从550 MPa增大到850 MPa，即屈服应力增大了300 MPa时，试件的整体弯曲变形降低了45.614 mm，δr降低了17.54 mm。显然，随屈服强度不断增大，屈服强度对整体弯曲变形和局部凹陷变形的影响都逐渐减小。双层管道变化趋势与单层管道类似。双层管道在相同屈服强度时冲击力大于单层管道，位移小于单层管道。另外，当屈服应力高于550 MPa时，屈服应力增加对冲击力和位移影响较小。结果表明，屈服强度高的材料抵抗冲击载荷的能力更强。

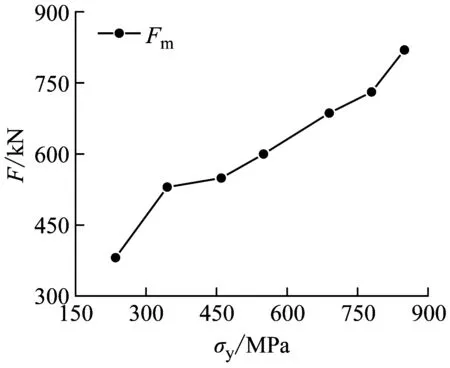
(a) G1冲击力

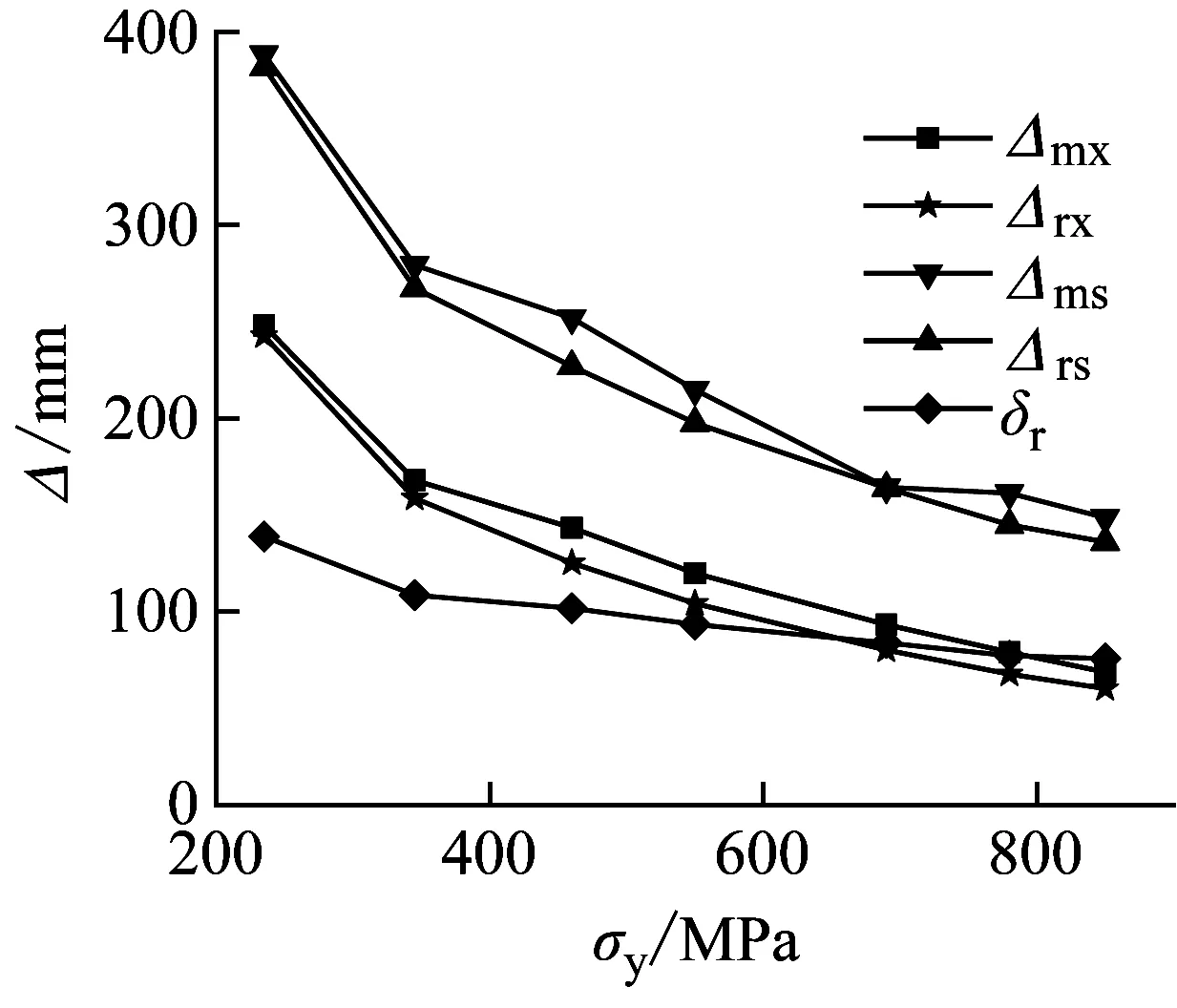
(b) G1跨中位移

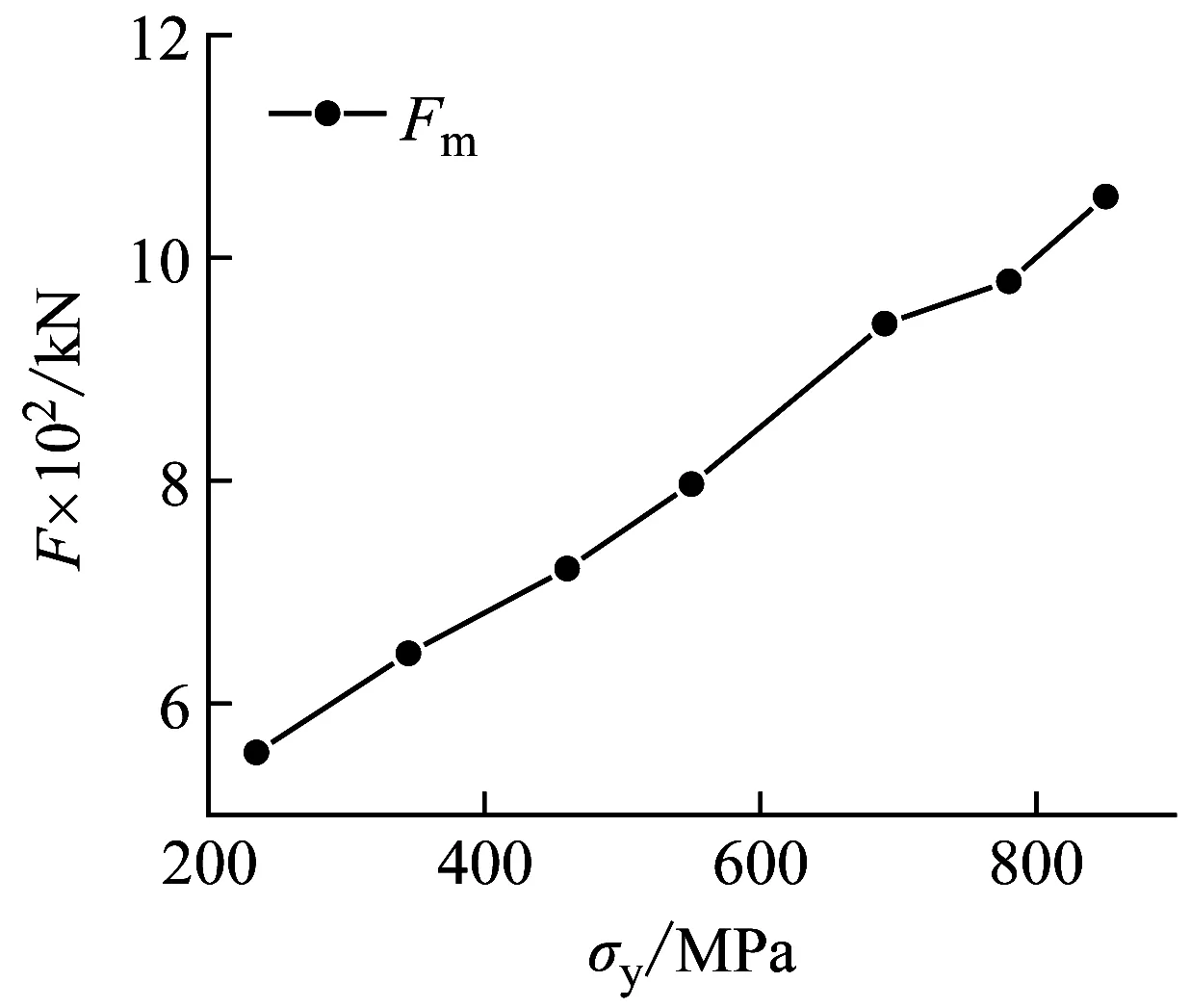
(c) G1-D冲击力

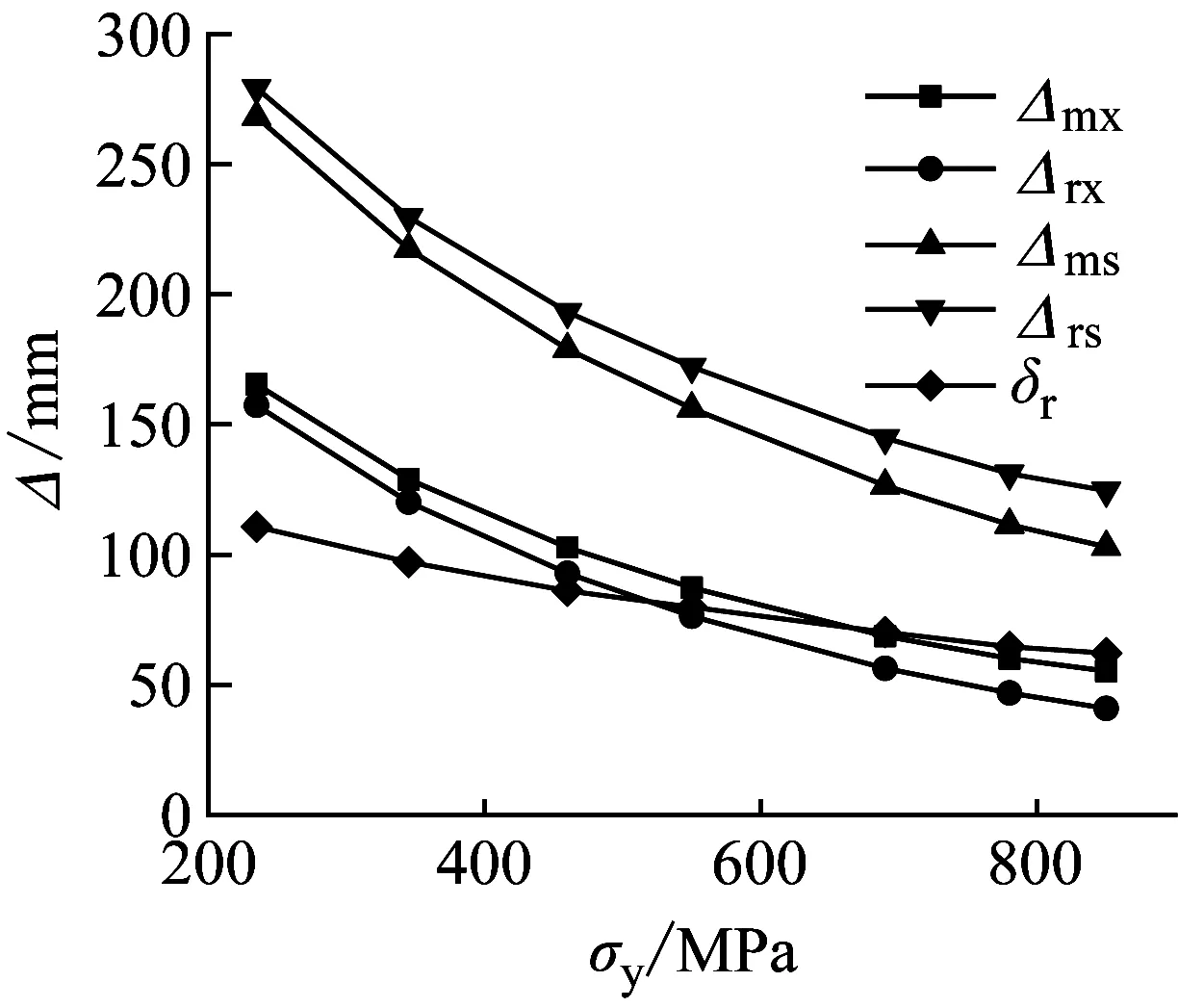
(d) G1-D跨中位移

4.3 径厚比影响(D0/t)

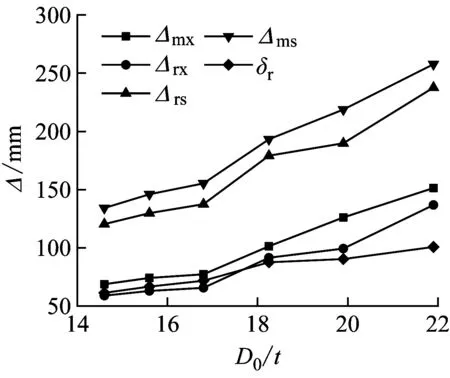
为获得径厚比D0/t对试件抗冲击性能的影响，保持管道直径D0不变，将管道壁厚t0分别取10 mm、11 mm、12 mm、13 mm、14 mm、15 mm进行模拟计算，即径厚比分别取值21.90、19.90、18.25、16.85、15.64、14.60。图14显示了G1和G1-D试件在相同冲击载荷作用下，Fm、Δmx、Δrx、Δms、Δrs以及δr随径厚比的变化趋势。可以看出，当径厚比D0/t增大时，最大冲击力Fm减小，Δmx、Δrx、Δms、Δrs以及δr随D0/t增大而增大。对比单双层管道冲击力和跨中变形，内层管的存在使双层管抗弯刚度增大，造成双层管的最大冲击力增大，位移减小。

4.4 长细比影响(λ)

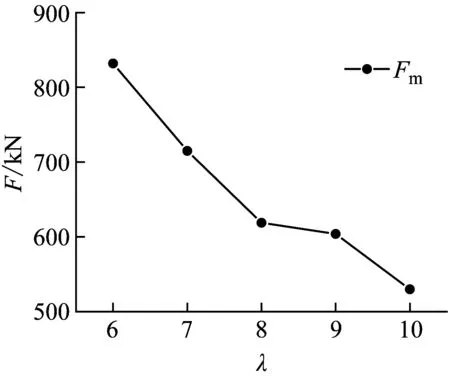
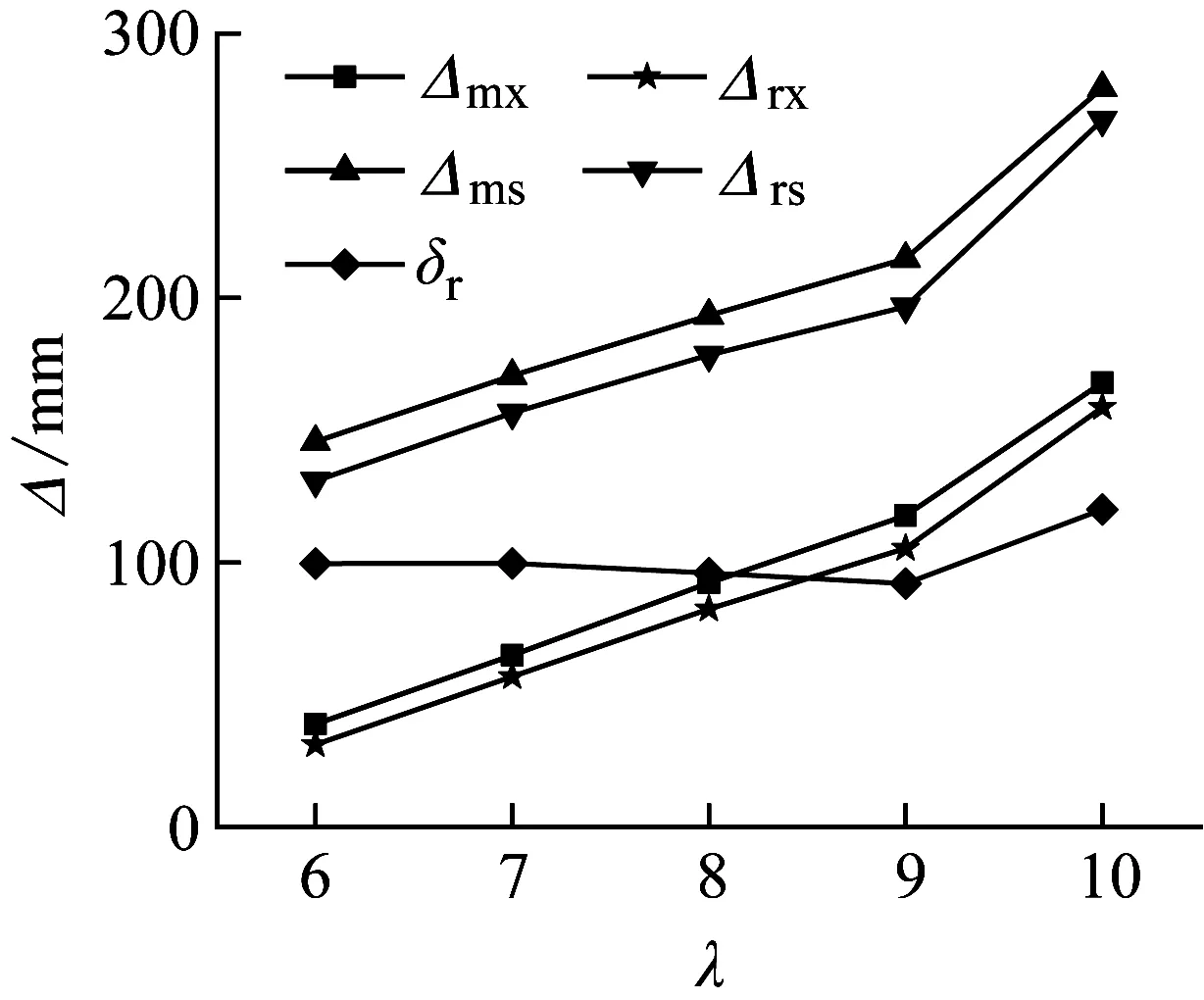
图15显示了不同长径比λ对Fm、Δmx、Δrx、Δms、Δrs和δr的影响。管道直径为219 mm，将管道长度L分别取1 314 mm、1 533 mm、1 752 mm、1 971 mm、2 190 mm，即长径比分别取值为6、7、8、9、10。单双层管道具有相似的变化规律。当试件直径相同，长径比λ增大时，Fm逐渐减小，Δmx、Δrx、Δms和Δrs不断增大。另外，当长细比λ从6增大到10时，局部变形δr在很小范围内波动。如图15(b)所示，当长细比从6增大到10时，即管道长度增大876 mm，单层管道G1的局部变形δr变化范围为102±6 mm，双层管道G1-D的局部变形δr变化范围为79.3±4.2 mm，显然，长细比λ对δr影响较小。这是由于试件的局部变形与横截面刚度直接相关，λ的变化不会影响试件的横截面刚度。当长细比λ增大时，试件的稳定性降低，因此Δmx、Δrx、Δms和Δrs增大。

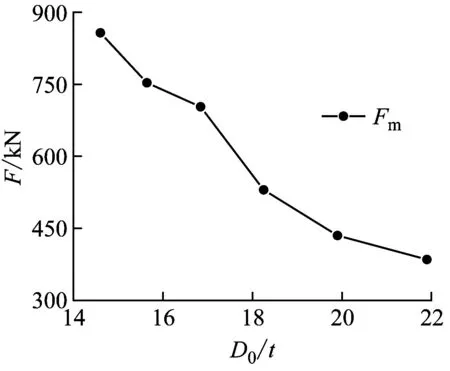
(a) G1冲击力

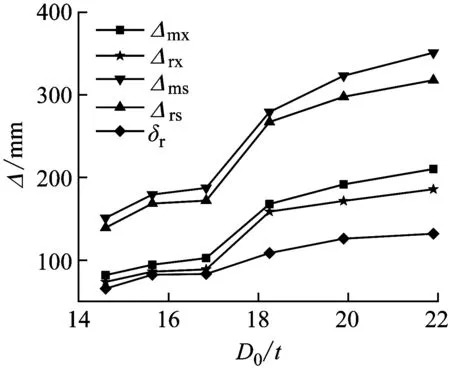
(b) G1跨中位移

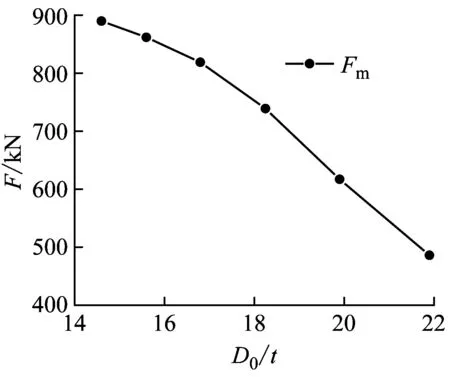
(c) G1-D冲击力

(d) G1-D跨中位移

(a) G1冲击力

(b) G1跨中位移

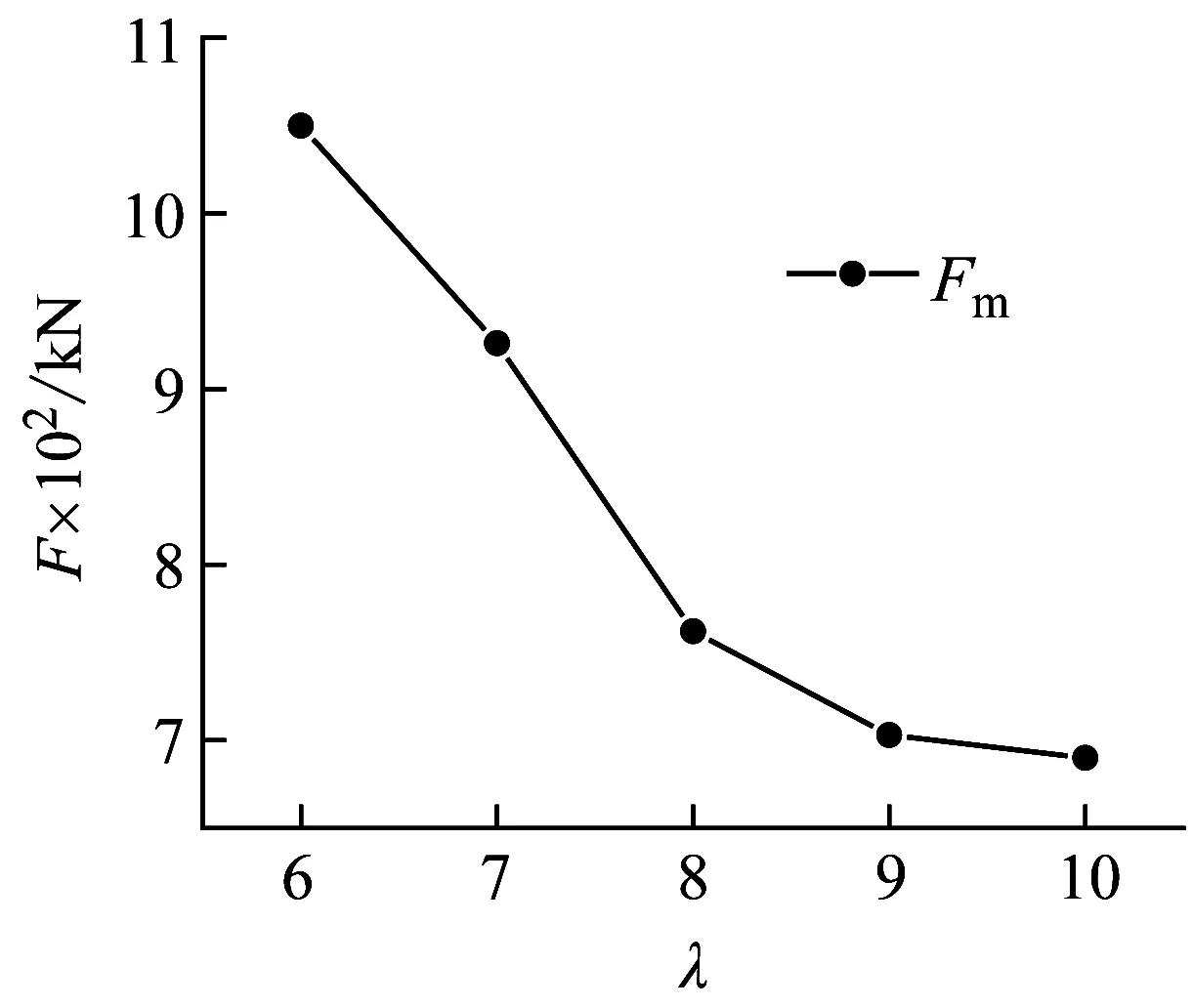
(c) G1-D冲击力

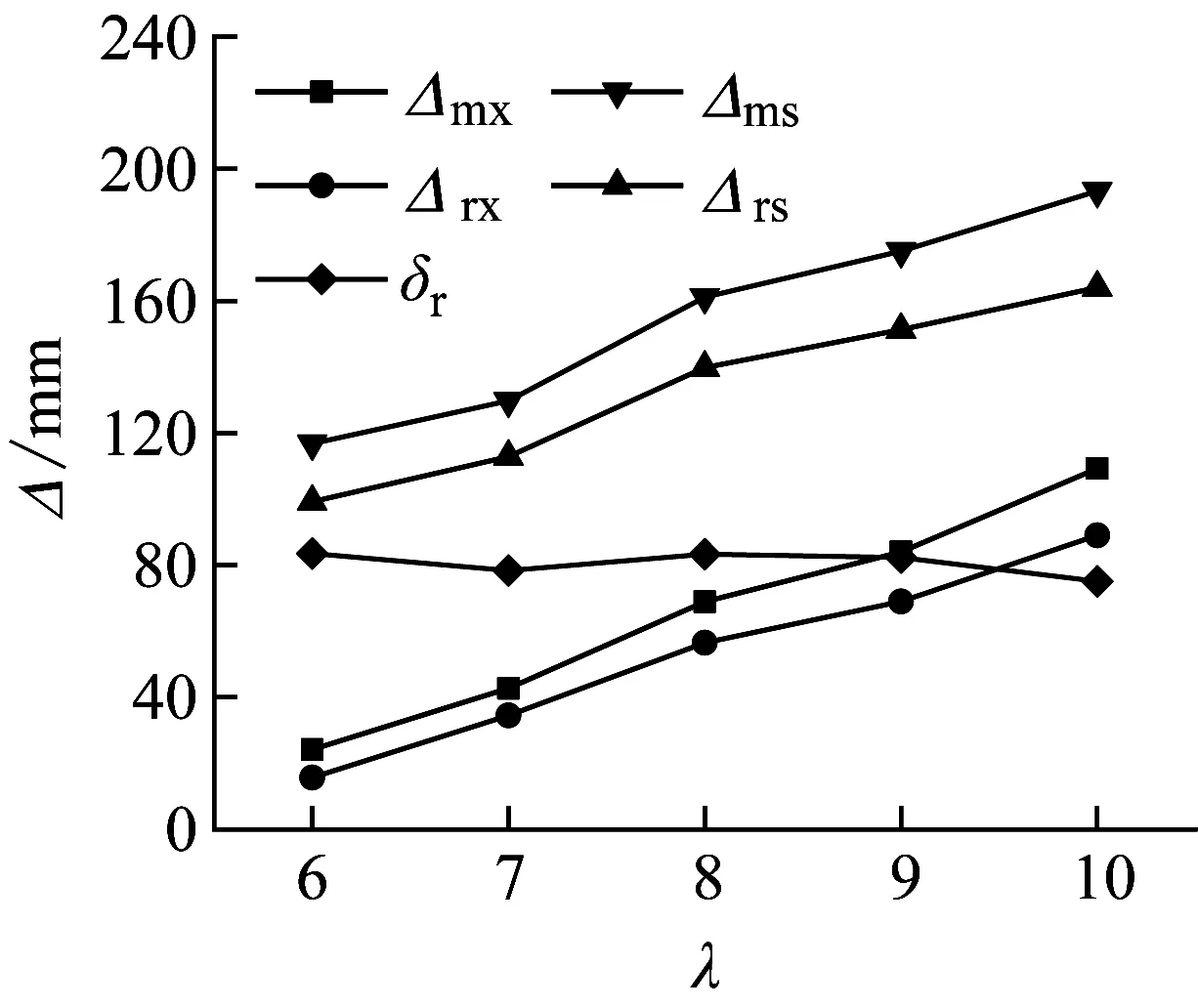
(d) G1-D跨中位移

5 结 论

采用实验和数值模拟相结合的方法，对单层和双层海底管道在横向冲击载荷作用下的抗冲击性能进行了落锤冲击试验，得到了海底管道的破坏模式，分析了管道的冲击力时程曲线、位移时程曲线和应变时程曲线等抗冲击性能参数。建立有限元模型，与试验结果进行对比验证，并进行参数分析，得到以下结论：

(1) 单层和双层海底管道在横向冲击作用下有相同的破坏模式。破坏模式是局部凹陷处弯曲屈服，由管道的整体弯曲变形与冲击凹痕部位的局部弯曲耦合形成。

(2) 对比单双层管道发现，双层海底管道有更好的抗冲击性能。这是由于内层管的存在使双层管抗弯刚度增大，同时内层管会阻止双层海底管道进一步发生变形。

(3) 建立与试验条件相同的有限元模型，可以准确地预测试件在横向冲击载荷作用下的的行为。数值模拟结果表明，试件在横向冲击载荷作用下的抗冲击性能受冲击高度、试件屈服强度、径厚比以及长细比的影响。冲击高度和厚度对抗冲击性能的影响较大。试件长细比影响较小。当采用相同的冲击能量时，屈服强度高的材料抗冲击能力更强。