一种基于多步回溯算法的铣削稳定性预测方法

于福航， 李茂月， 严复钢， 刘献礼， 梁越昇

(1. 哈尔滨理工大学 机械动力工程学院， 哈尔滨 150080；2. 佐治亚理工学院 乔治W.伍德拉夫机械工程学院， 亚特兰大 30318)

薄壁类零件由于其轻便、高效的结构特性被广泛地应用于航空航天、汽车制造和国防领域[1]。然而，薄壁类零件由于其低刚度，弱阻尼等特点往往不利于铣削过程中的稳定切削，甚至引发颤振，最后影响加工工件的表面质量和加工效率等[2]。在薄壁类零件铣削过程中，颤振产生的最主要原因之一就是再生效应[3]。因此，考虑再生效应的薄壁工件铣削颤振预测仍是目前学术界和工业研究的热点问题[4]。

铣削稳定性预测在选择合适的加工参数以实现无颤振加工中起到了重要的作用。最常用的稳定性预测方法就是通过预测稳定性叶瓣图以显示切削深度与主轴转速之间的临界关系，从而在稳定切削区域选择切削参数[5]。早在20世纪，由Tobias等[6]最早提出再生颤振，随后又由Tlusty等[7-8]阐明了自激振动现象。此后，各国学者据此针对铣削稳定性开展了大量的研究工作，并提出了一系列地稳定性预测方法。这些方法主要聚焦于如何更加快速和准确地构建稳定性叶瓣图，可分为频域解析法和时域法。

频域解析方法以Altintas等[9]提出的零阶频域法(单频率法，ZOA)为代表，该方法通过将周期铣削力系数与近似系统进行变换，再根据稳定性判据计算轴向切深临界值，随后Ozturk等[10]将该方法推广到五轴球头刀铣削加工稳定性分析，Altintas团队也通过这种方法分析了不等齿距[11]、变螺旋角[12]等因素对铣削稳定性的影响，但由于忽略了傅里叶级数中的高次项，这种方法的计算精度无法满足小径向切深时的要求[13]。针对这一问题，Merdol等[14]基于已完成的工作，提出了一种多频率法，该方法被开发用于低浸没式铣削，可以同时满足小径向切深和大径向切深的要求，但由于使用了高阶项进行近似，因此计算时间被大大地加长了。

时域法最初由Insperger等[15-16]提出，即半离散法(Semi-Discretization Method,SDM)，该算法是通过对铣削时滞微分方程中延迟项进行离散化处理后进行计算，随后又提出了一种高阶的半离散法[17]来近似周期性时滞系统。Ding等[18]通过提出一种全离散法(Full-Discretization Method，FDM)来预测铣削稳定性，包括一阶全离散法(1stFDM)和二阶全离散法(2ndFDM)，这种方法是通过线性插值对状态项和延迟项进行离散化处理，进而求出近似的数值解的方法。Guo等[19]通过将全离散法中的Euler插值变成Newton插值，提出了一种三阶全离散法，并具有比一阶、二阶全离散法更高的计算精度和更快的计算效率。Li等[20]通过对微分方程的状态项、延迟项、微分项全部离散化，提出了一种完全离散法(CDSEM)。Li等[21]基于完全离散法，提出了一种完全离散化的龙格库塔方法(RKCDM)来预测铣削过程中的稳定性问题。Jiang等[22]基于改进的精确时间积分算法，开发了一种高效的二阶半离散法(2ndSDM)，大大提高了原半离散算法的计算效率。

在随后的研究中，为了在满足一定预测精度的同时提高预测效率，各国学者对铣削稳定性的预测方法逐渐由线性单步法转变为线性多步法。Eksioglu等[23]最早提出将Simpson公式应用于铣削稳定性的求解过程中，随后Zhang等[24]详细地比较了基于Simpson公式的铣削稳定性预测方法(SBM)与其他算法的计算精度和计算效率。Zhang等[25]基于泰勒公式，采用差分法和外推法的思想，提出一种数值微分的铣削稳定性预测方法。智红英等[26]根据隐式Adams公式提出了一种铣削稳定性预测方法，该方法较1stFDM和2ndFDM方法具有收敛速度快的优点，随后智红英等[27]又提出了一种基于Hamming公式的铣削稳定性预测算法，并得到了高于1stFDM和2ndFDM的计算精度。Dai等[28]提出一种显式精细积分法(PIM)来预测铣削过程的稳定性，该方法可以显著降低由差分格式引起离散化误差，从而提高计算精度。

在考虑过程阻尼铣削稳定性预测算法的研究中，Tlusty等[29]最先指出了随着切削速度降低，稳定性边界有所提高，并将其归结为过程阻尼效应的影响。随后，Wu[30]指出过程阻尼主要来源于刀具后刀面压入工件的材料体积，并提出了一种基于压入体积和过程阻尼系数的过程阻尼力模型。Budak等[31]将过程阻尼当作附加阻尼纳入动力学模型中，随后采用简单实验法获取稳定性极限。近两年，Wan等[32]提出了一种通过分离实测铣削力中的静态过程阻尼力直接辨识过程阻尼系数的通用方法。Li等[33]提出了一种考虑过程阻尼效应的二阶半离散法用于预测铣削过程的稳定性。

然而，目前考虑过程阻尼的铣削稳定性预测算法仍然较少，且对于附加过程阻尼力的求解比较耗时。针对这一问题，本文提出考虑过程阻尼效应的一种多步回溯算法，能够有效地提高求解的效率和精度。

1 铣削动力学模型

切削过程颤振发生的原因可分为再生型振动、摩擦型振动和模态耦合型振动等，通常认为再生型振动为颤振发生的主要原因，如图1所示。

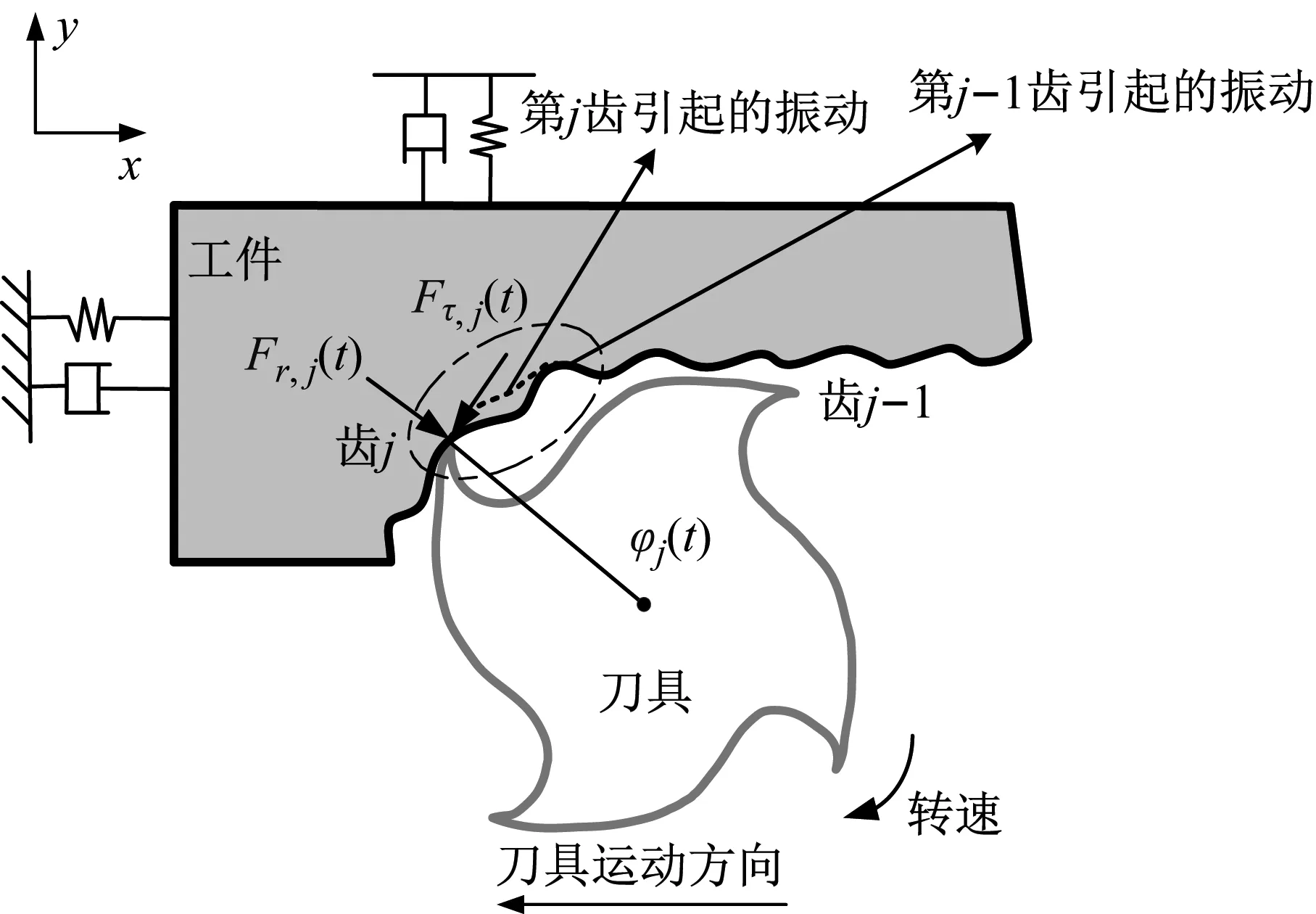
图1 二自由度铣削模型中再生效应示意图

而在低速铣削区域，铣削稳定性极大地受到源于刀具和工件间接触处产生的过程阻尼效应的影响[34]。过程阻尼主要来源于刀具后刀面与工件波纹表面之间的干涉作用，通常被认为是一种能量转移或消散机制，可以有效提高低速铣削的稳定性，如图2所示。

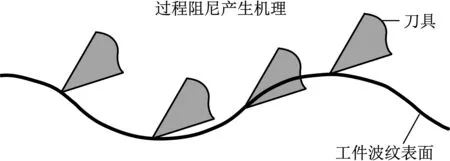
图2 过程阻尼产生机理示意图

Ahmadi等[34]指出，过程阻尼可以用等效黏性阻尼表示为

(1)

式中：Ceq为等效阻尼系数；Ksp为压痕系数；W为刀具后刀面的磨损带宽度；ap为轴向切削深度；切削速度v=πDΩ/60，D表示刀具直径。

通过铣削动力学模型对再生型振动和过程阻尼进行建模，表达式如式(2)所示

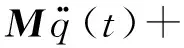
(2)

式中：M、C和K分别是刀具的模态质量、模态阻尼和模态刚度矩阵；ap是切削过程中的轴向切深；t为切削的瞬时时刻；q(t)为刀具模态坐标；H(t)为周期切削力系数矩阵；G(t)为过程阻尼力系数矩阵；T为时滞量且等于刀齿切削周期，T=60/(NΩ)，且N为刀具齿数，Ω为刀具主轴转速，单位为r/min。

通过考虑过程阻尼的铣削模型来预测铣削稳定性，采用刚性刀具-柔性工件系统，以X和Y方向上具有相等的模态参数的双自由度铣削动力学模型为例，可简化为一个两自由度铣削系统，如图1所示。其铣削动力学模型可由式(2)表示为

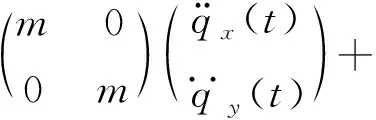
其中，切削力系数表达式为

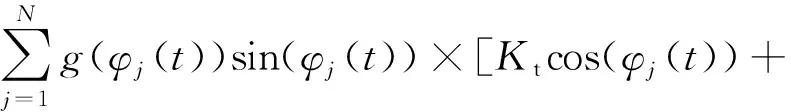
Knsin(φj(t))],

Knsin(φj(t))],

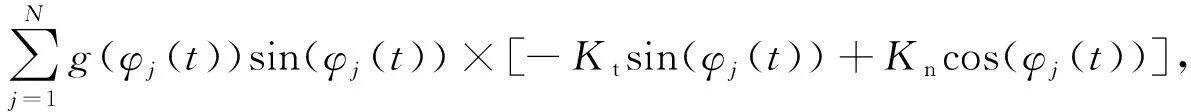
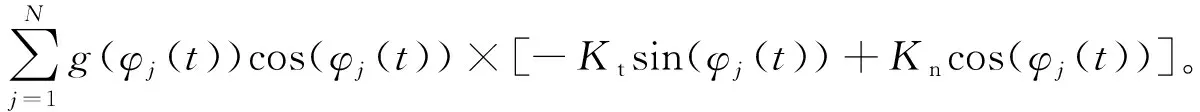
过程阻尼系数表达式为

gxx(t)=

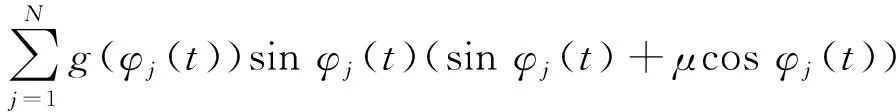
gxy(t)=

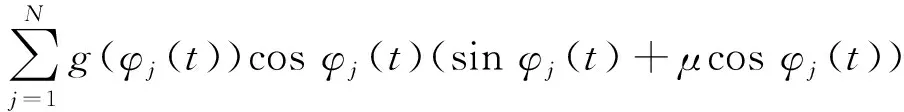
gyx(t)=

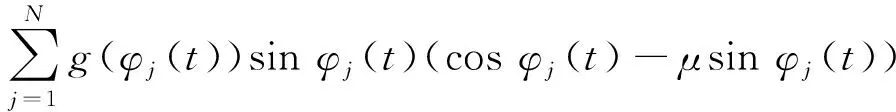
gyy(t)=

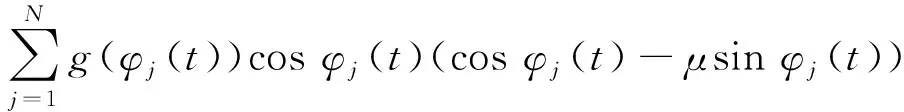
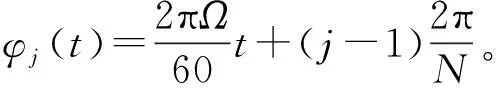
式中：φst是刀具的切入角；φex是刀具的切出角。顺铣时，φst=arccos(2a/D-1)，φex=π；逆铣时，φst=0，φex=arccos(1-2a/D)，其中a/D为径向切深与刀具直径之比。

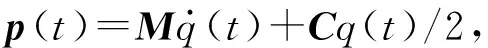
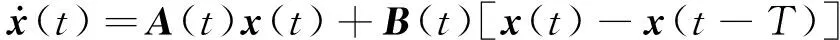
(3)

式中，A(t)和B(t)为由再生效应和过程阻尼效应决定的周期系数矩阵。其中，

(4)

(5)

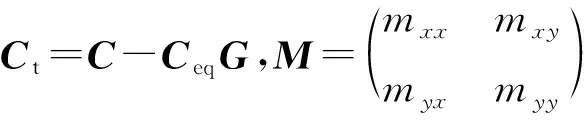
综上，对于考虑再生颤振和过程阻尼的铣削稳定性预测可以转换为对式(3)的求解。

2 一种多步回溯算法

在一些难加工(如钛合金)薄壁件的铣削稳定性加工中，由于材料加工特性的影响，导致其加工的切削速度不易过高，进而在一定程度上限制了铣削加工的主轴转速，而由于低速区域稳定性边界起伏变化比中速和高速区域快的多，即导致同一种算法的一个离散步内(假设均以单位1为离散步长)，高速区域达到精度要求时，在低速区域达不到精度要求，如图3所示。

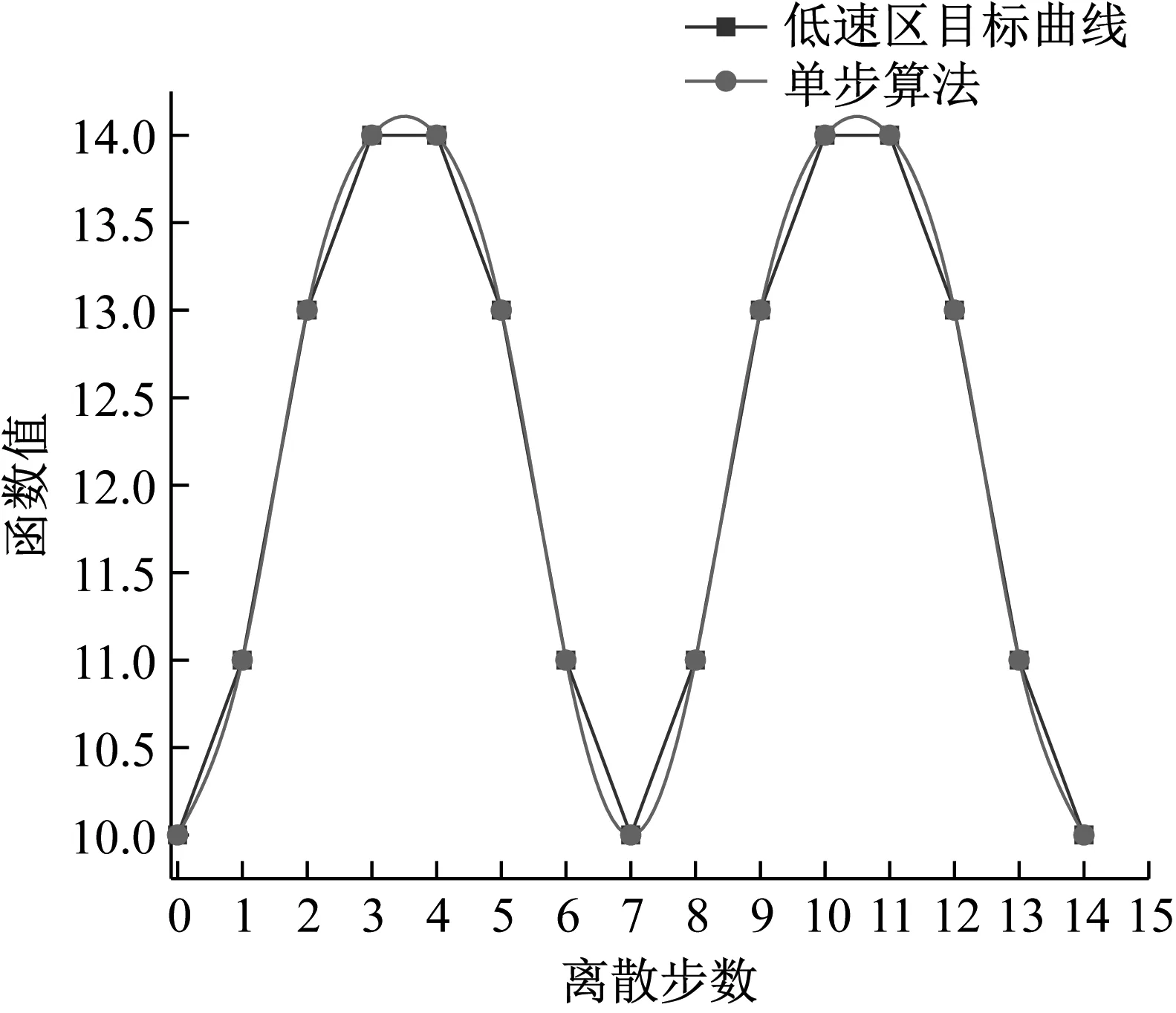
(a) 稳定性边界低速区示意图

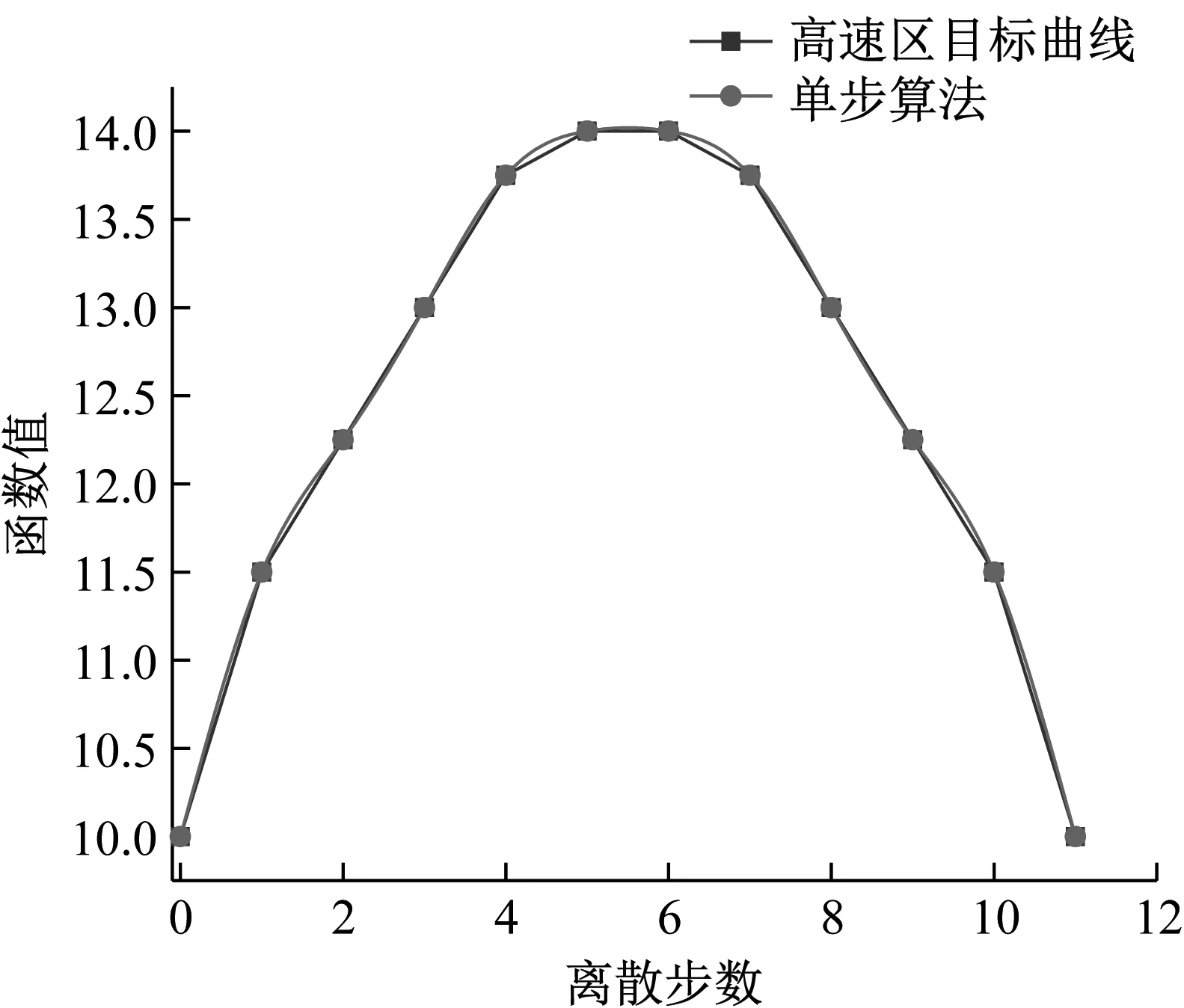
(b) 稳定性边界高速区示意图

本文从这个角度出发，通过采用多步回溯插值算法，在确保算法在全局稳定性预测精度的基础上，提高其在主轴转速低速区间的收敛速度，并以收敛率及计算精度作为算法的评价指标。在全离散法的基础上，对状态方程的时滞项进行多步插值近似，从而提出一种多步回溯算法来预测铣削过程中的稳定性。

设铣削过程的初始时刻为t0，通过状态空间变换方法，式(3)可以解为如下形式

(6)

式中：T为刀齿切削时间周期且等于时滞量；τ为将T等距间隔离散后的每个离散区间。

由于刀齿切削的时间周期T可分为两个阶段，即自由振动阶段t∈[t0,t0+tf]和强迫振动阶段t∈[t0+tf,t0+T]。当刀具处于自由振动阶段，状态值如下所示

x(t)=eA(t-t0)x(t0)

(7)

当刀具处于强迫振动阶段时，即t∈[t0+tf,t0+T]，通过离散化的思想将强迫振动的时间等距分成m个时间区间，且每个时间区间的长度可以表示为τ=(T-tf)/m，则每个区间的时间点为

ti=t0+tf+(i-1)h(i=1，…，m+1)

(8)

当t∈[ti,ti+1]时，代入式(6)，原方程可化为

x(t)=eA(t-ti)x(ti)+

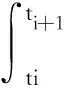
(9)

采用线性多步法的思想对状态量x(t)进行插值计算，由于本文提出的多步回溯算法步数k(k≤4,且k∈N*)取值的不同会影响计算的精度和计算效率，故本节给出不同k取值时算法的计算式，并重点推导回溯步数k=4时算法的计算过程。

当t=t1时，即处于初始时刻时，状态量

x(t1)=x(t0+tf)=eAtfx(t0)=eAtfx(tm+1-T)

(10)

为简化表达式，用Ai+1表示A(ti+1)，则不同回溯步数k的第i个离散点算法计算式可表示为

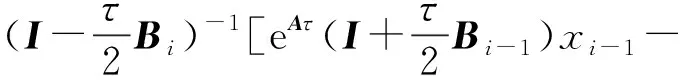
(11)

xi=

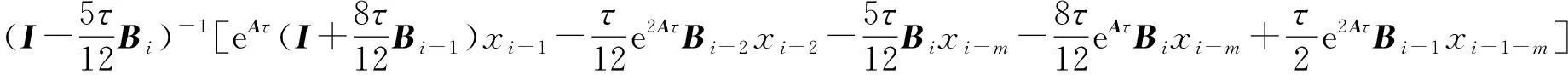
(k=2)

(12)

xi=

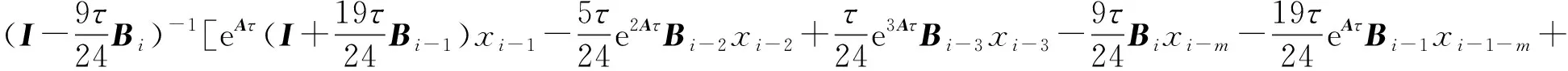
(13)

xi=

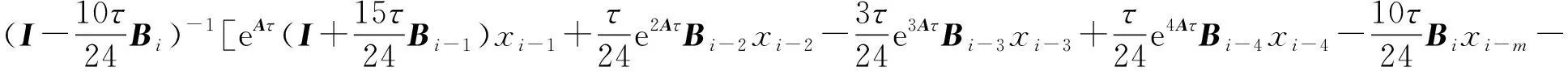
(14)

本文以k=4为例，则式(14)可以被简化为

xi=(I+Fi)-1[(F0+Fi-1)xi-1+Fi-2xi-2+

(15)

其中，F0=eAτ，

式中，

Bi1=Bi+(Bi-1-Bi)/τ，

Bi2=Bi-1+(Bi-2-Bi-1)/τ，

Bi3=Bi-2+(Bi-3-Bi-2)/τ，

Bi4=Bi-3+(Bi-4-Bi-3)/τ。

若式中[I-Fi]-1非奇异，令F=(I+Fi)-1，将式(15)代入到式(3)中可得离散映射为：yi+1=Diyi。

其中，向量yi可以定义为

yi=col(xi,…,xi-1,…,xi-m,…,xi-4-m)

式中，col(xi,…,xi-1,…,xi-m,…,xi-4-m)表示将括号里的列向量xi，…，xi-1，…，xi-4-m等集合成一个矩阵yi。

则Di可以定义为

其中，当k=4时，Di可表示为

综上，在一个切削时间周期内的状态传递矩阵D可以通过Floquet理论构建为

ym=Dm-1，…，D1D0y0=Dy0

(16)

即：D=Dm-1，…，D1D0

(17)

根据李雅普诺夫理论可知，系统的稳定性与状态传递矩阵的特征值有关，据此可获得铣削系统的稳定性叶瓣图。

首先建立考虑过程阻尼效应的铣削动力学模型，通过将过程阻尼力看成是阻尼矩阵的附加项进行求解，并提出一种多步回溯算法计算模型的状态传递矩阵，算法计算流程如图4所示。

其中，eig()表示取特征值，abs()表示取绝对值，max()表示取最大值。

3 算法数值仿真分析

3.1 不同算法收敛率比较

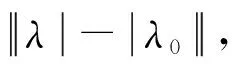
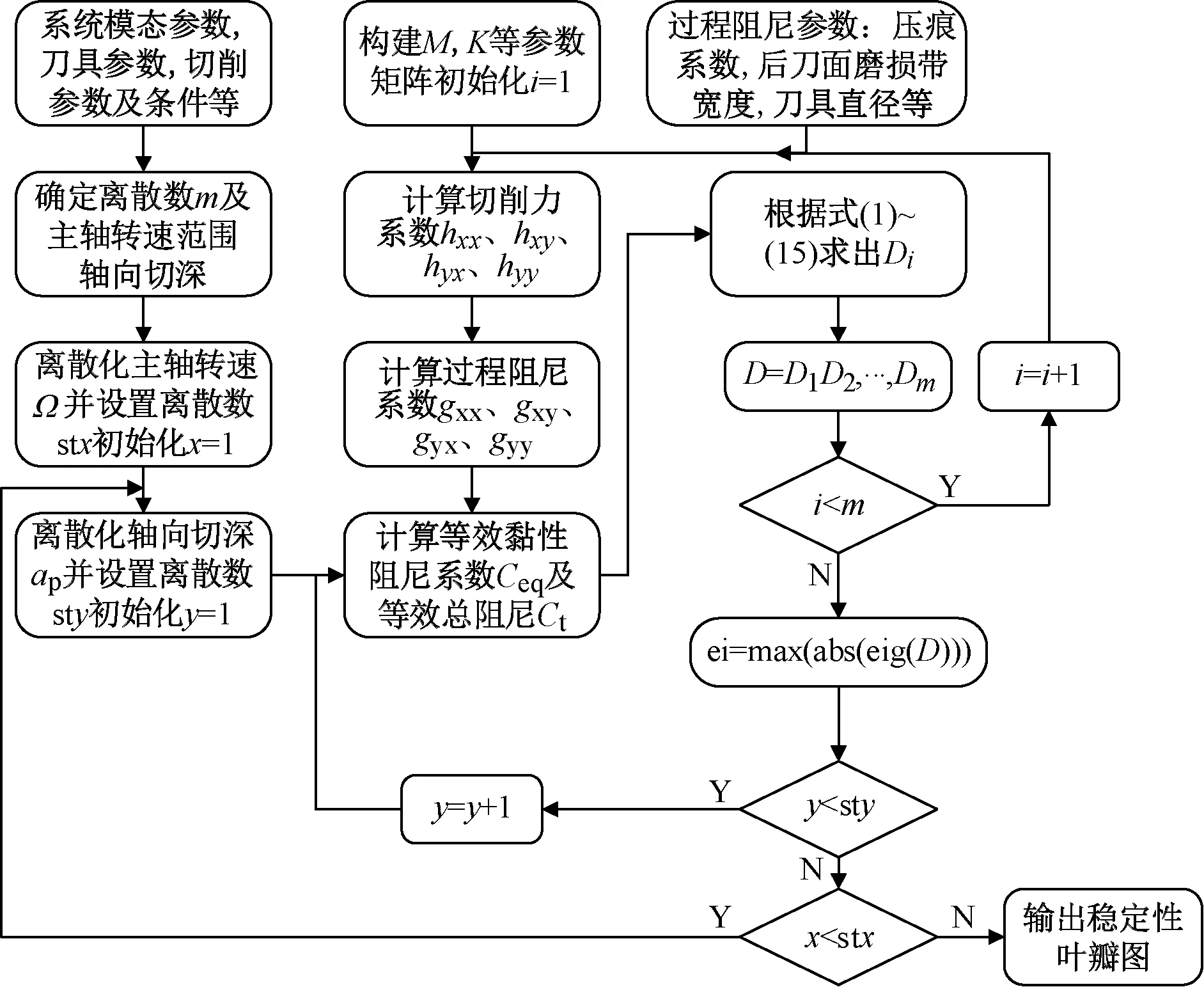
图4 基于多步回溯算法预测铣削稳定性流程图

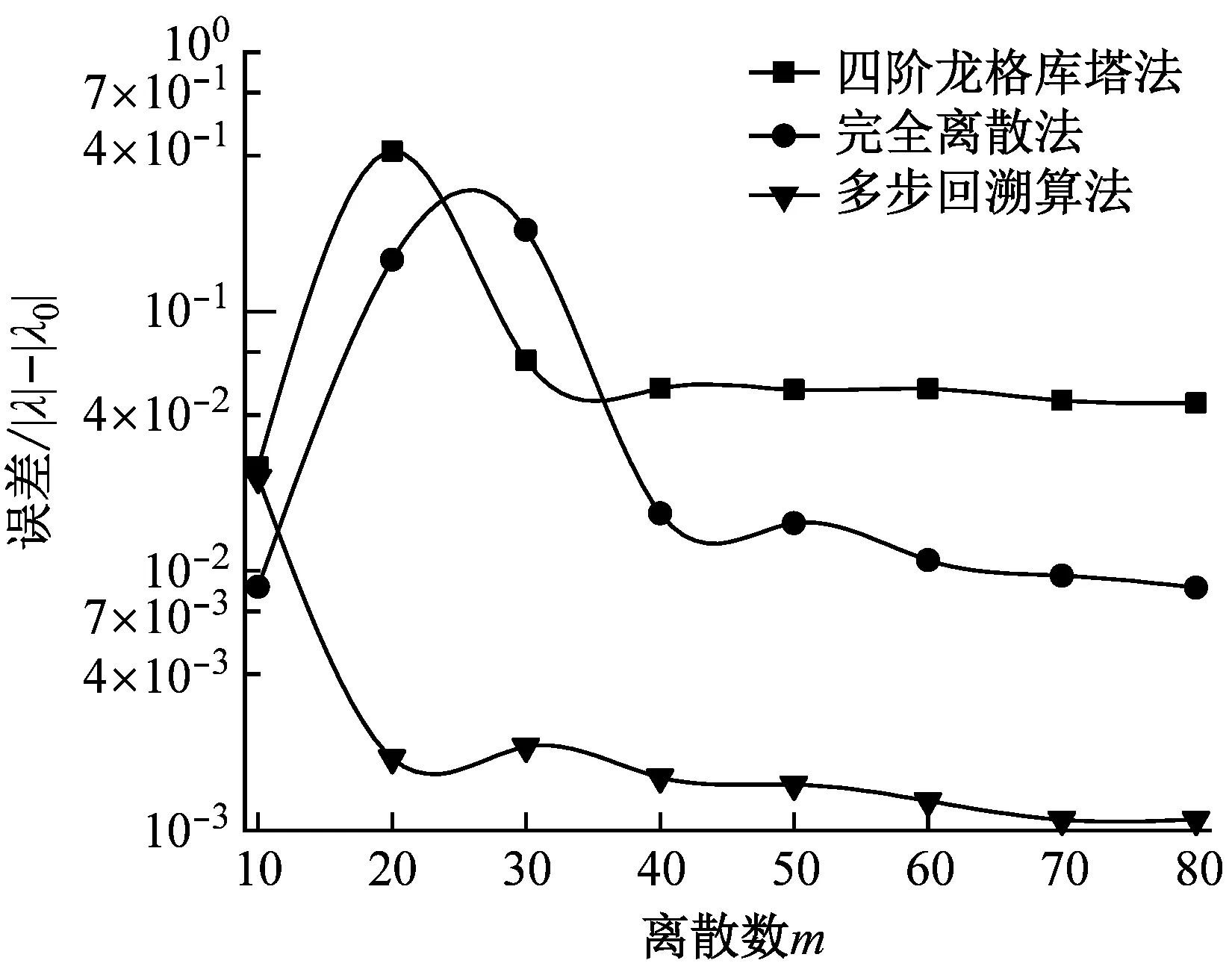
同时，为揭示本文提出算法的收敛率，本节采用双自由度铣削动力学模型进行计算，由于四阶龙格库塔法和完全离散法具有较高的收敛速度，下面选择这两种算法作为参照组与本文提出的算法进行比较，并将加工的系统参数设置为与参考文献[18]中所采用的参数相同。本文所用的具体系统参数及加工参数设置如表1所示。得到不同算法不同离散数m的收敛率曲线如图5所示。

表1 系统参数及加工参数

图5揭示了不同算法之间收敛率的快慢。由图5不难看出，在相同的切削条件下，所提出的多步回溯算法比四阶龙格库塔法和完全离散法具有更高的收敛效率。具体来说，当m=20时，多步回溯算法的收敛率已基本趋于平稳，而图中其它算法的收敛率在m=50时才基本趋于平稳，且误差值较m=20时的多步回溯算法大。

3.2 算法稳定性预测误差分析

在实际预测中，在低速铣削区域，由于过程阻尼的影响常常使得稳定性区域进一步地扩大。常用的具有较高收敛速度的四阶龙格库塔法和完全离散法无法直接进行考虑过程阻尼的铣削动力学方程的求解。故本文选择近两年提出的二阶半离散法作为对照组进行仿真计算，并将参数与参考文献[33]设置相同，实验参数如表2所示，得到稳定性预测叶瓣图如图6所示。

(a) ap=0.6 mm, |λ0|=0.973 4

(b) ap=1.2 mm,|λ0|=0.093 7

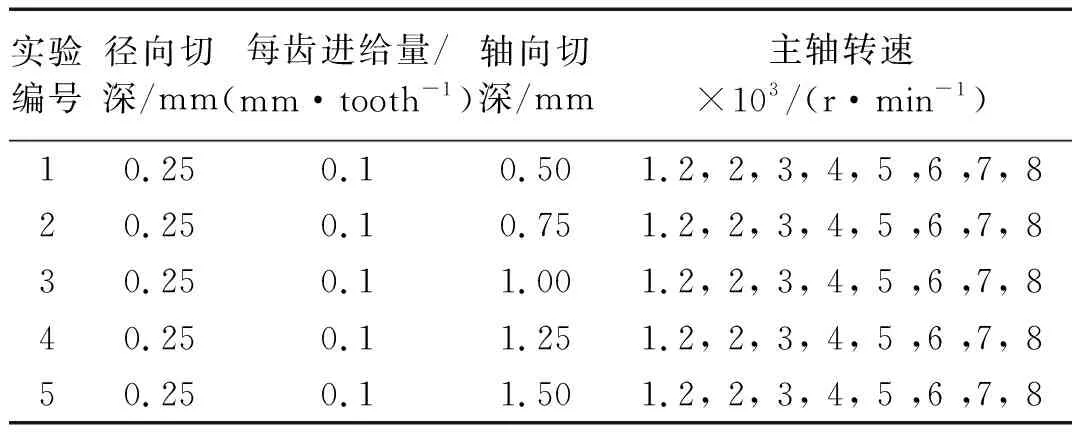
表2 铣削稳定性验证实验参数[33]

图6(a)为引用参考文献[33]二阶半离散法的预测图，图6(b)为本文提出的多步回溯算法的预测图，图中的颤振点、边界点、稳定点均为文献[33]中的实验数据点。计算时间由MATLAB软件在同一台计算机[Intel®Core(TM) i5-3210M 2.50 GHz]上运算得出。

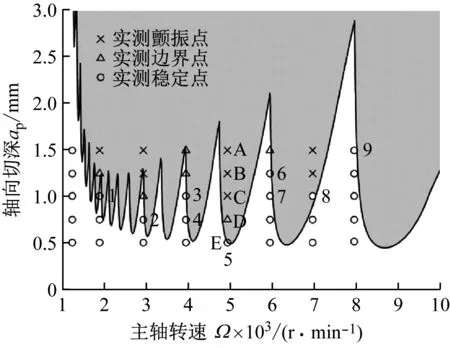
(a) 二阶半离散法[33]m=80,时间t=2 138 s

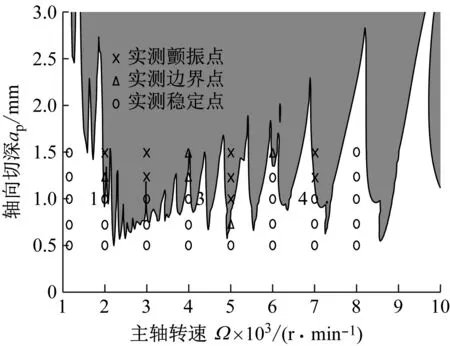
(b) 多步回溯算法m=50,时间t=763 s

为进一步分析所提出算法的预测精度，本文引入了边界预测误差(Boundary Prediction Error, BPE)的概念。边界预测误差为预测边界上出现实测颤振点和稳定点占实测总数的百分比。

边界预测误差的计算如式(18)所示

(18)

式中：Ne为预测边界出现实测非边界点的个数；Nt为实测总点数。

从图6(a)和6(b)中不难看出，文献[33]中的二阶半离散算法的预测边界出现实测非边界点的个数Ne=9，文中提出的多步回溯算法预测边界出现实测非边界点的个数Ne=4。根据式(18)可求出不同算法的BPE，如表3所示。

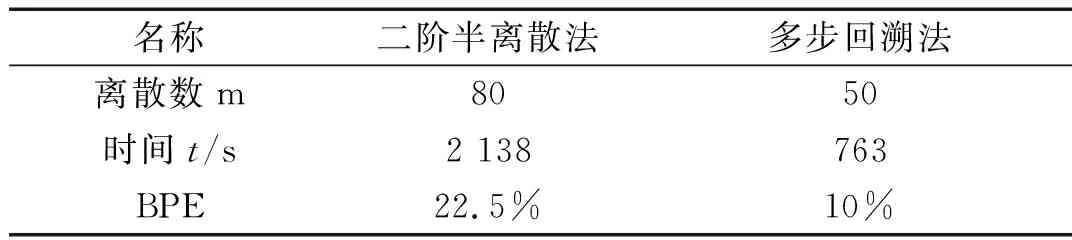
表3 考虑过程阻尼效应不同算法的计算时间及BPE

由表3可知，当多步回溯算法的离散数m=50时，其边界预测误差较二阶半离散法减少了约12.5%，其计算时间也缩短了约64.3%。

4 结 论

本文重点研究了使用基于多步回溯算法对铣削稳定性的预测，并从该研究中得出以下结论：

(1) 将动态铣削系统抽象为具有单个时间延迟的微分方程，通过微分方程理论可导出系统的一般解，并采用根据多步插值的思想对一般解进行离散化，最后采用Floquet理论确定铣削条件的稳定性，最后获得稳定性叶瓣图。

(2) 通过与四阶龙格库塔法和完全离散法在收敛速度与计算精度方面进行比较，结果表明：多步回溯算法可以在确保全局计算精度的前提下，对于低主轴转速铣削区域具有更高的收敛速度，这种特性尤其适合一些铣削速度不高的难加工材料(例如钛合金)的铣削预测。

(3) 通过多步回溯算法与考虑过程阻尼效应的二阶全离散法的比较，结果表明：如果设置小于二阶全离散法(m=80)的离散数，多步回溯算法(m=50)的边界预测误差较二阶半离散法减少了约12.5%，其计算时间也缩短了约64.3%。

综上所述，本文提出的多步回溯算法具有一定地快速收敛及高计算精度等特点，尤其在低速铣削的稳定性预测中具有良好的应用前景。