基于三阶剪切变形理论的压电功能梯度板静力学等几何分析

刘 涛， 李朝东， 汪 超， 蒋雅芬， 刘庆运

(1.上海大学 机电工程与自动化学院，上海 200072； 2.安徽工业大学 机械工程学院，马鞍山 243002； 3.安徽工业大学 创新教育学院，马鞍山 243002)

功能梯度材料(Functionally Graded Material, FGM)[1]是指沿着某方向连续性改变材料结构或组成的材料，如在厚度方向，材质从金属过渡到陶瓷材料。因其独特的力学优势，目前被广泛应用于航空、核能、生物医学、机械等领域[2-4]。同样作为智能材料，压电材料独有的正逆压电效应[5]，使其在结构的健康监测[6]和微机电系统[7]领域中发挥着重要作用。因此，将压电材料与FGM结合以获得性能更加优越的智能结构和智能材料，引起了国内外学者的广泛关注。

压电智能结构的迅速发展使其结构形式变得更加多样化、复杂化。因此，结构的自由振动[8-9]、弯曲[10-12]、屈曲[13]、振动[14]、形状控制等问题的研究愈发受到重视[15]。压电智能结构分析的建模方法主要有解析法建模、数值方法建模和实验方法建模。压电功能梯度板(Piezoelectric Functionally Graded Plate, PFGP)是最基本的压电功能梯度材料结构形式之一，就其结构分析的数值分析方法看，采用常规的三维弹性理论框架，传统的数值方法会耗费大量计算网格。若要提高计算效率，则需要根据材料属性定制对应的形函数[16]改进数值方法(如梯度有限先法)。然而，这种改进方式仍然摆脱不了维度上带来的网格自由度增量。为解决上述问题，国内外很多学者采用等效单层理论[17]框架下的数值方法去研究PFGP的力学行为。He等与Liew等分别在经典板理论(Classical Plate Theory, CPT)和一阶剪切变形理论(First-Order Shear Deformation Theory, FSDT)的框架下，利用有限单元法(Finite Element Method, FEM)研究了PFGP在机-电-热载荷下的静力学、动力学特性和主动振动控制问题。此外，为解决FEM中因单元畸变降低计算精度[18-19]的问题，文献[12-14]采用无网格法(Mesh-Free Method)研究了PFGP的屈曲、静态响应、形状控制以及振动等问题。Loja等[20]建立了高阶剪切变形理论(Higher-Order Shear Deformation Theory, HSDT)框架下的B样条有限元模型，文中有效分析了PFGP的静态响应与自由振动问题。结合HSDT和冯·卡尔曼方程(Von Kármán Euqations)，Fakhari等[21-22]又采用有限单元法研究了热环境下PFGP的非线性自由、强迫振动等问题。上述板理论中，CPT仅对薄板有效而不具有通用性；FSDT因阶次过低而可能会导致分析精度稍弱；而HSDT构造过程过于复杂而不利于数值分析的离散化过程。相对而言，三阶剪切变形理论(Third-Order Shear Deformation Theory, TSDT)因利用C1连续单元提高求解的精确度且无需引入剪切因子具有明显的优势。目前，已有一批学者将TSDT的数值方法运用到功能梯度梁、板及壳体的力学分析中[23-25]。在PFGP的研究中，Selim等[26]构建了TSDT框架下的无网格法，文中研究了两种不同结构的PFGPs的主动振动控制问题。

但就上述的数值方法(有限单元法或无网格法)而言，若研究对象的几何体稍作复杂，则会出现计算分析模型和几何模型不一致的现象[27]。为解决此类问题，Hughes提出一种新的力学数值算法——等几何分析(Isogeometric Analysis, IGA)[28]。其基本思想是将计算机辅助设计(Computer Aided Design, CAD)的非均匀有理B样条(Non-Uniform Rational B-Splines, NURBS)作为计算机辅助工程(Computer Aided Engineering, CAE)的形函数，方便地实现任意连续阶次的平滑性。与传统的数值方法相比，IGA这种统一的数学方程，即省去了CAD与CAE数据之间的交互，又避免了如有限元使用拉格朗日多项式差值函数带来的逼近误差。可以说，理论上IGA形成了CAD与CAE的无缝连接。鉴于IGA方法自身的诸多优点以及其天然地满足TSDT所需的C1连续性要求[29]的特性，使得部分学者将TSDT与IGA方法结合对FGM结构的静力学[30]、动力学[31-32]、结构与材料参数优化[33-34]等问题进行了研究，验证了该方法的精确性。

最近，少部分学者将IGA方法引入到PFGP的分析中。如，Phung-Van等[35]分析了PFGP在机-电-热负载下的非线性瞬态响应；Nguyen等[36]研究了压电功能梯度多孔板的静动态响应；Nguyen-Quang[37]则针对均匀、V型、X型以及O型四种体积分数分布形式，分析了集成压电层的功能梯度碳纳米管增强复合材料板的动态响应。值得注意的是，在PFGP静力学问题中，构建三阶剪切变形理论的等几何分析方法还未被涉及，因此，本文拟用TSDT下的IGA方法，研究并探讨PFGP的自由振动、弯曲以及变形控制等静力学问题。

1 基于三阶剪切变形理论的压电功能梯度板模型

如图1所示，PFGP长为a，宽为b，共分为上、中、下三层。中间层厚度为hf，是由金属和陶瓷组成的功能梯度材料，在厚度方向上其材质具有光滑连续的变化特性。中间层上、下表面均被一厚度为hp的压电层完全覆盖，忽略中间层与压电层之间的胶黏层。板的总厚度ht=hf+2hp。

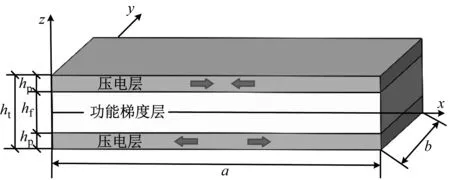
图1 压电功能梯度板

1.1 功能梯度层的体积分数

假设金属材料的体积分数含量在厚度方向上为幂函数形式分布

(1)

Vc(z)=1-Vm(z)

(2)

则功能梯度板内任意一点的材料的物性参数为

P(z)=(Pm-Pc)Vm(z)+Pc

(3)

式中:下标c和m分别为非金属和金属;z为厚度方向上的坐标(z∈[-hf/2,hf/2]);n为功能梯度指数n∈[0,∞];Pc和Pm分别为非金属和金属的相关材料属性，如：密度、弹性模量或者泊松比等。

1.2 三阶剪切变形理论

由Reddy[38]提出的TSDT，可得到PFGP内部任意一点的位移为

u(x,y,z)=u0(x,y)+zβx+c1z3(βx+w0,x)

v(x,y,z)=v0(x,y)+zβy+c1z3(βy+w0,y)

w(x,y,z)=w0(x,y)

(4)

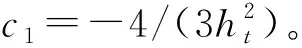
由几何方程可得几何非零应变为

(5)

其中，面内应变与横向剪切应变分别为

ε={εxxεyyγxy}T=ε0+zκ1+z3κ2

(6)

γ={γxzγyz}T=εs+z2κs

(7)

式中:ε0={u0,xv0,yu0,y+v0,x}T,

κ1={βx,xβy,yβx,y+βy,x}T，

κ2=c1{βx,x+w0,xxβy,y+w0,yyβx,y+βy,x+2w0,xy}T，

εs={βx+w0,xβy+w0,y}T

κs=3c1{βx+w0,xβy+w0,y}T

由广义胡克定律，应力的本构关系可以表示为

(8)

弹性常量为

Q66=G12,Q44=G23,Q55=G13

(9)

式中，E，v分别为弹性模量与泊松比。

实际应用中，压电材料常处于第二类边界条件，即力学夹持和电学短路[39]。根据第二类压电方程[40]，PFGP的本构方程可表示为

(10)

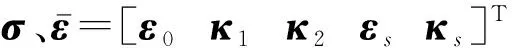
(11)

式中，压电应力常数e31、e32可以通过式(12)获得。

(12)

式中，d31，d32为压电应变常数。

仅考虑z方向上的电场强度，对应的电场强度矩阵表示为

(13)

式中，φ为压电层厚度方向上的电势差。

根据上述分析，PFGP的应变能为

(14)

因此，弹性刚度矩阵为

(15)

式中，

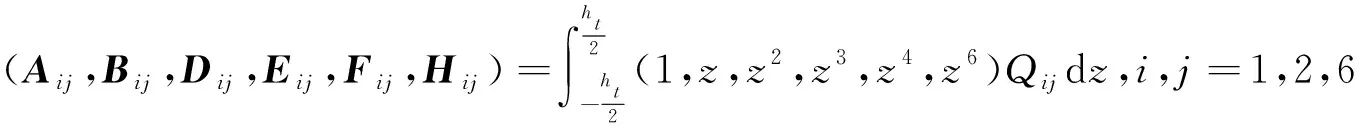
(16)

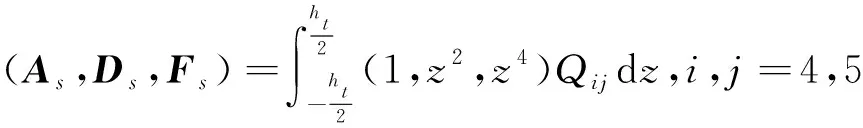
(17)

1.3 弱形式

利用哈密顿变分原理[41]，板的弱形式表示为

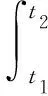
(18)

式中，t1和t2分别为时间轴的某两个时刻，L为总能量

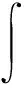
(19)

2 压电功能梯度板的等几何分析

2.1 NURBS基函数

节点矢量k(ξ)由一组单调不递减的实数序列组成[42]。定义为k(ξ)={ξ1=0,…,ξi,…,ξn+p+1=1}，其中ξi称为节点，n为基函数个数，p为样条阶次。Ni,p(ξ)表示第i个p次B样条基函数

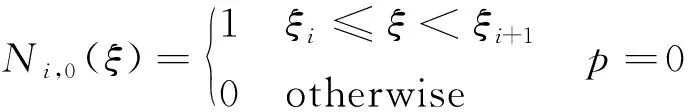
(20)

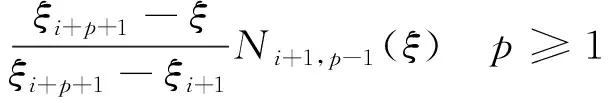
(21)

对于二维平面问题，NURBS基函数由两个方向的一维B样条基函数张量积构成

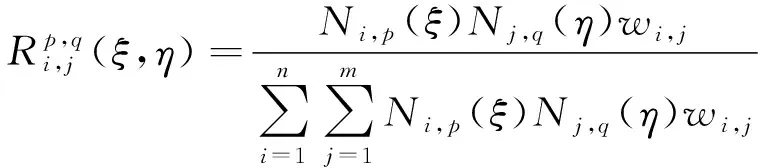
(22)

式中:wi,j为权重;Ni,p(ξ)和Nj,q(η)分别为ξ方向p阶次和η方向q阶次的B样条基函数，Nj,q(η)形式和Ni,p(ξ)类似。

2.2 机械位移场离散化

利用NURBS基函数，PFGP的近似机械位移场u(ξ,η)可表示为

(23)

其中，dI=[u0Iv0IβxIβyIwI]T为未知量，是控制点I的位移矢量。RI(ξ,η)为式(21)所定义的形函数。将式(23)代入式(6)和(7)，得到

(24)

其中，

2.3 电势场离散化

在近似电势场时，可分别将上、下压电层沿着厚度方向离散为多个子层单元。假设电势在每个子层厚度方向上的变化为线性[43]，则压电层的近似电势场可以描述为

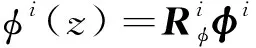
(26)

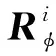
φi=[φi-1φi] (i=1,2,…,nsub)

(27)

式中，nsub为压电子层的总数量。

这里，假定每个压电子层单元同一高度的电势相同，则由式(13)可得每个子层单元的电场为

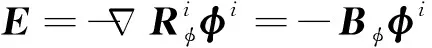
(28)

2.4 控制方程

将式(10)、(24)、(26)、(28)代入式(18)，可得压电功能梯度板的运动控制方程为

(29)

式中:Muu为质量矩阵；Kuu为PFGP的刚度矩阵，Kφφ为压电材料的自适应刚度矩阵；Kuφ与Kφu为机电耦合刚度矩阵；f为机械载荷；Q为压电层表面的电荷面密度等效节点电量。其值分别为

(30)

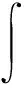
(31)

(32)

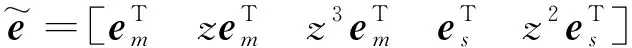
(33)

N={N1N2N3}T

(34)

(35a)

(35b)

(35c)

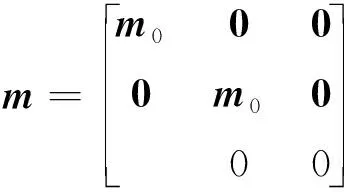
(36)

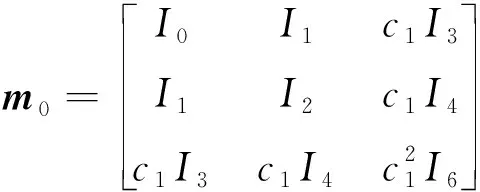
(37)

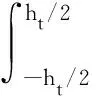
(38)

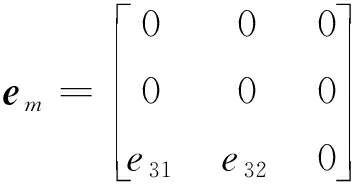
(39)

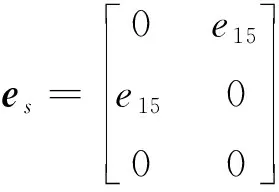
(40)

因此，Kuφ可以重写为

(41)

将式(29)的第二行，代入第一行消去电势φ，可以得到

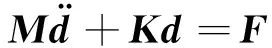
(42a)

M=Muu

(42b)

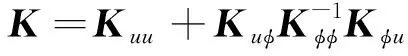
(42c)

最后，静力学、自由振动的问题可描述为

Kd=F

(43)

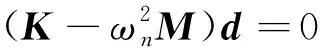
(44)

式中:ωn为第n阶固有频率;K和M分别为整体刚度矩阵、质量矩阵。

2.5 压电功能梯度板变形控制

PFGP的变形控制主要分为开环控制和闭环控制。开环控制时，上下压电层都作为驱动器时，当外部输入压电作用于压电层，电压将转化为驱动力。通过调整输入电压的大小改变结构的位移，达到控制结构变形的目的。而在闭环控制中，一个压电层作为驱动器，另一个压电层作为传感器。通过反馈控制原理，结构在机械载荷作用下产生机械变形，传感器层感知结构的变形而产生相应的输出电压。该感应电压通过控制器控制增益放大后，作为驱动器的输入电压，驱动器由于逆压电效应产生相应的反驱动力抑制结构的变形，从而达到控制结构变形的目的。

因此，闭环控制中，式(29)的第二行可以改写为

[Kφu]ad-[Kφφ]aφa=Qa

(45)

[Kφu]sd-[Kφφ]sφs=Qs

(46)

式中,下标a，s分别为驱动器层和传感器层。

根据位移反馈控制规律，驱动器的输入电压φa表示为

φa=Gdφs

(47)

式中，Gd为位移反馈控制增益系数。

静态变形中，对于传感器层，外部电荷Qs=0。忽略逆压电效应，则由式(46)可得，结构变形传感器层所产生的电势为

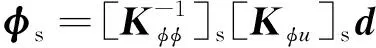
(48)

将式(47)、(48)代入式(45)可得

(49)

最后，将上式代入(43)，整理可得

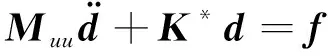
(50)

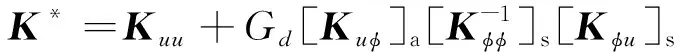
(51)

3 数值算例

为方便起见，在本文后续章节中，将板的机械边界条件简写为：简支(S)，固支(C)，自由(F)。此外，基函数阶次均取为p=q=3。

3.1 收敛性分析

为验证所提方法的收敛性与适用性，本节以一个尺寸为400 mm×400 mm(a×b)的压电功能梯度板为例。板的中间层是由Ti-6Al-4V和Aluminum oxide组成的功能梯度材料，厚度hf=5 mm。由式(1)可知，当功能梯度指数n=0时，中间层是材料为Ti-6Al-4V的均质板。当n=∞时，为Aluminum oxide。两块沿z向极化，厚度为hp= 0.1 mm的PZT-G1195N压电层完全覆盖在中间层的上、下表面。该板的材料参数如表1所示。

如图2所示，本文利用4种不同控制点数目的IGA计算网格验证所提方法的收敛性与精确性。表2为对应4种计算网格下，边界条件为SSSS的压电功能梯度板的第1、2、4、6、8阶固有频率。由表2可知，本文所提方法计算结果与文献[44]的解析解计算结果吻合程度较高。此外，在控制节点大于19×19时，本文方法对计算结果的影响较小，可以判断，该网格自由度下，本文方法已经达到了收敛状态。因此，本文后续算例均采用的控制节点数目为19×19。表3列举了控制节点数目19×19下，边界条件为CFFF和CCCC的PFGPs的前6阶固有频率。通过与文献[8]的有限单元法计算结果相比，验证了所提方法对于其他机械边界条件压电功能梯度板的适用性。同时，由表1、2可知，随着功能梯度指数n的增大，固有频率增大。

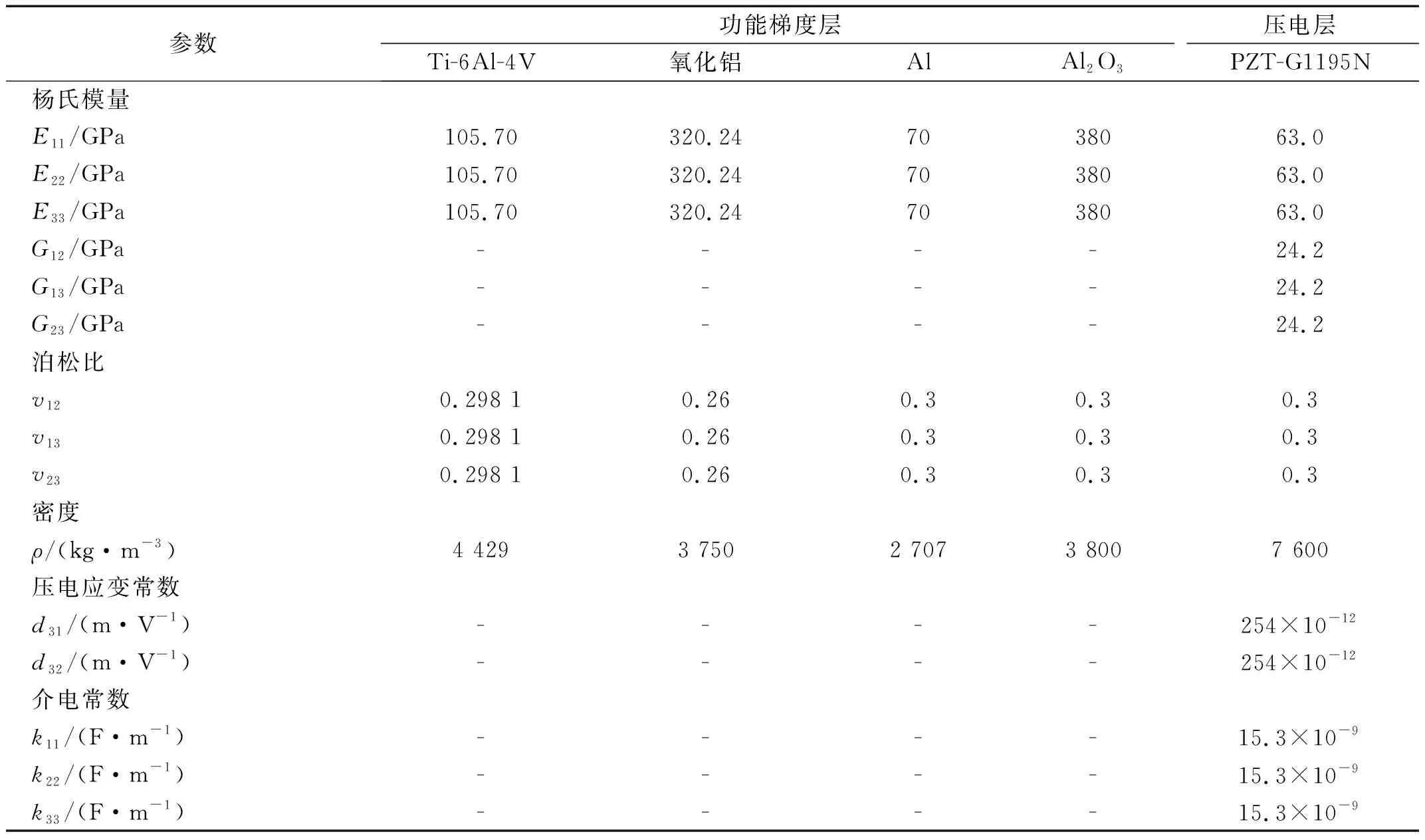
表1 材料参数

(a) 9×9

(b) 15×15

(c) 19×19

(d) 21×21

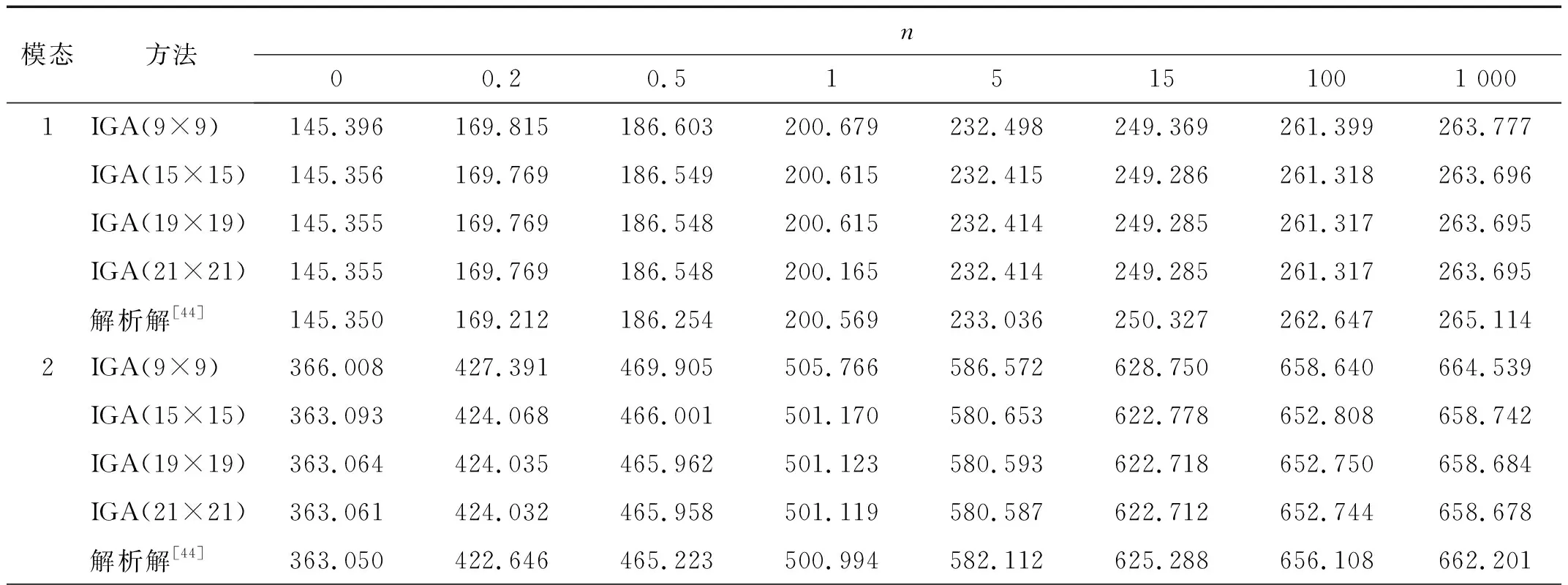
表2 不同网格下，四边简支(SSSS)PFGP的1、2、4、6、8阶固有频率

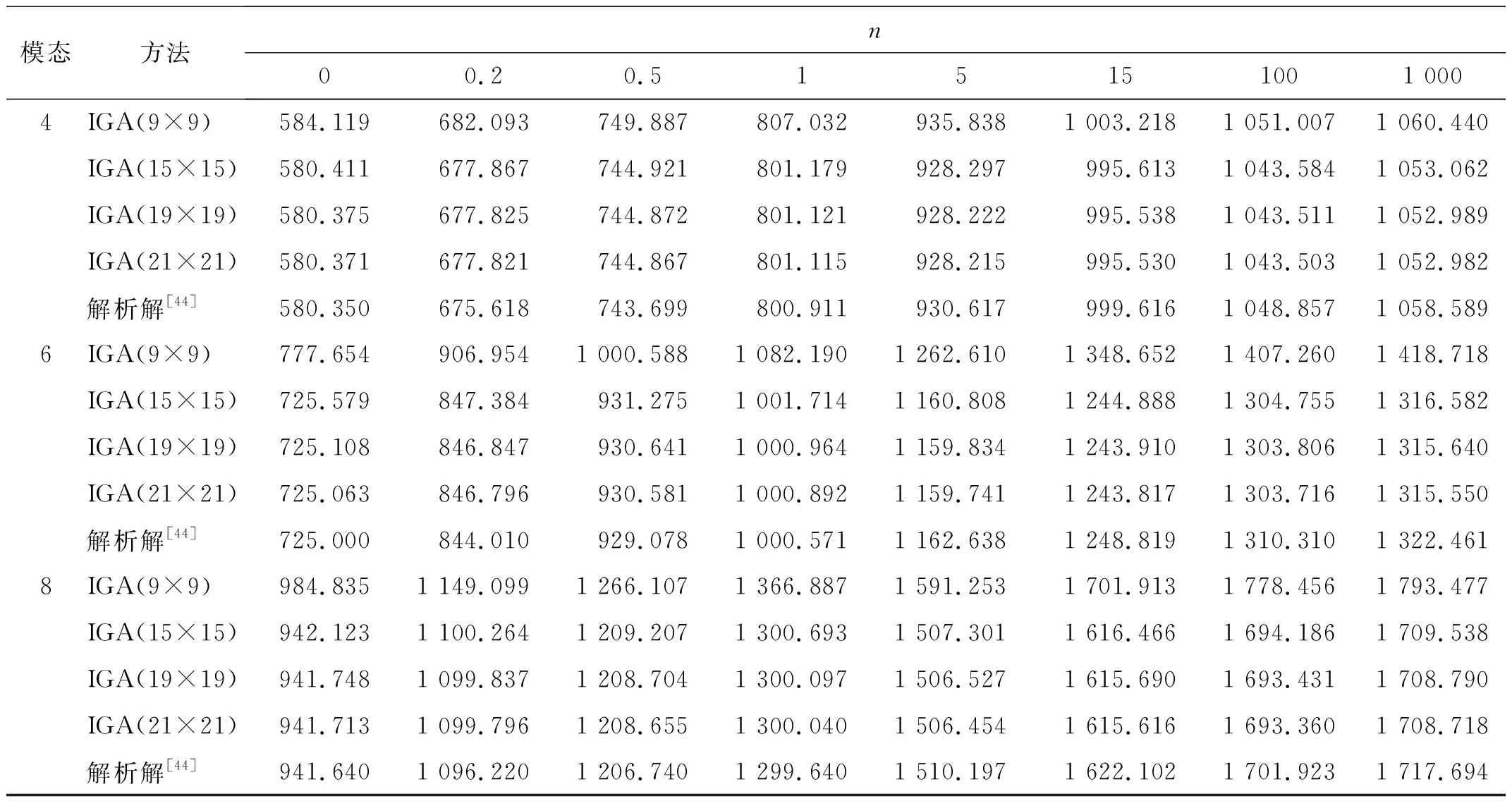
表2(续) Hz

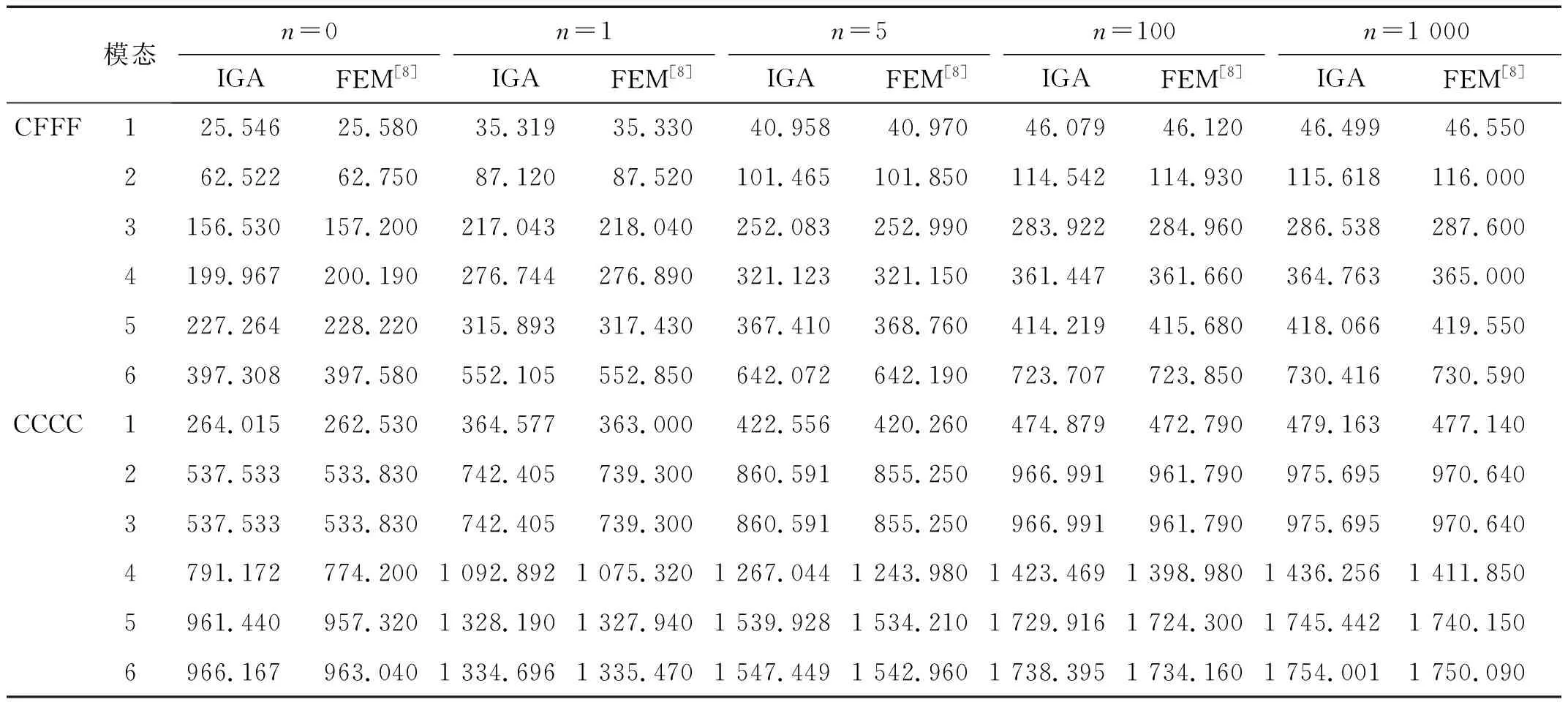
表3 悬臂(CFFF)、四边固支(CCCC)的PFGPs的前6阶固有频率

3.2 自由振动问题分析

本节，以一个中间层由Al和Al2O3组成，上下压电层的材料为PZT-4的PFGP为例，研究电学边界条件(短路和开路)对其固有频率的影响(PZT-4的材料参数见文献[44])。值得注意的是，在本节中，当功能梯度指数n=0时，中间层是材料为Al2O3的均质板。当n=∞时，为Al。

表4列出了功能梯度层的宽厚比(hf/a)、压电层与功能梯度层厚度比(hp/hf)、功能梯度指数n以及电学边界条件对四边简支(SSSS)的PFGP的1、2阶固有频率的影响。表5列举了宽厚比为0.02(hf/a=0.02)、压电层与功能梯度层厚度比为0.1(hp/hf=0.1)、机械边界条件为SSSC和SCSC的PFGP的前6阶固有频率。

由表4、5可知：开路状态下板的固有频率大于短路状态；随着功能梯度指数n增加，板的金属材料成分增加，刚度减小，固有频率也减小；另外，当功能梯度层厚度与板长之比(hf/a)由0.05增加到0.1时，板的固有频率也增加近一倍。图3则为开路状态下板的前6阶固有振型。

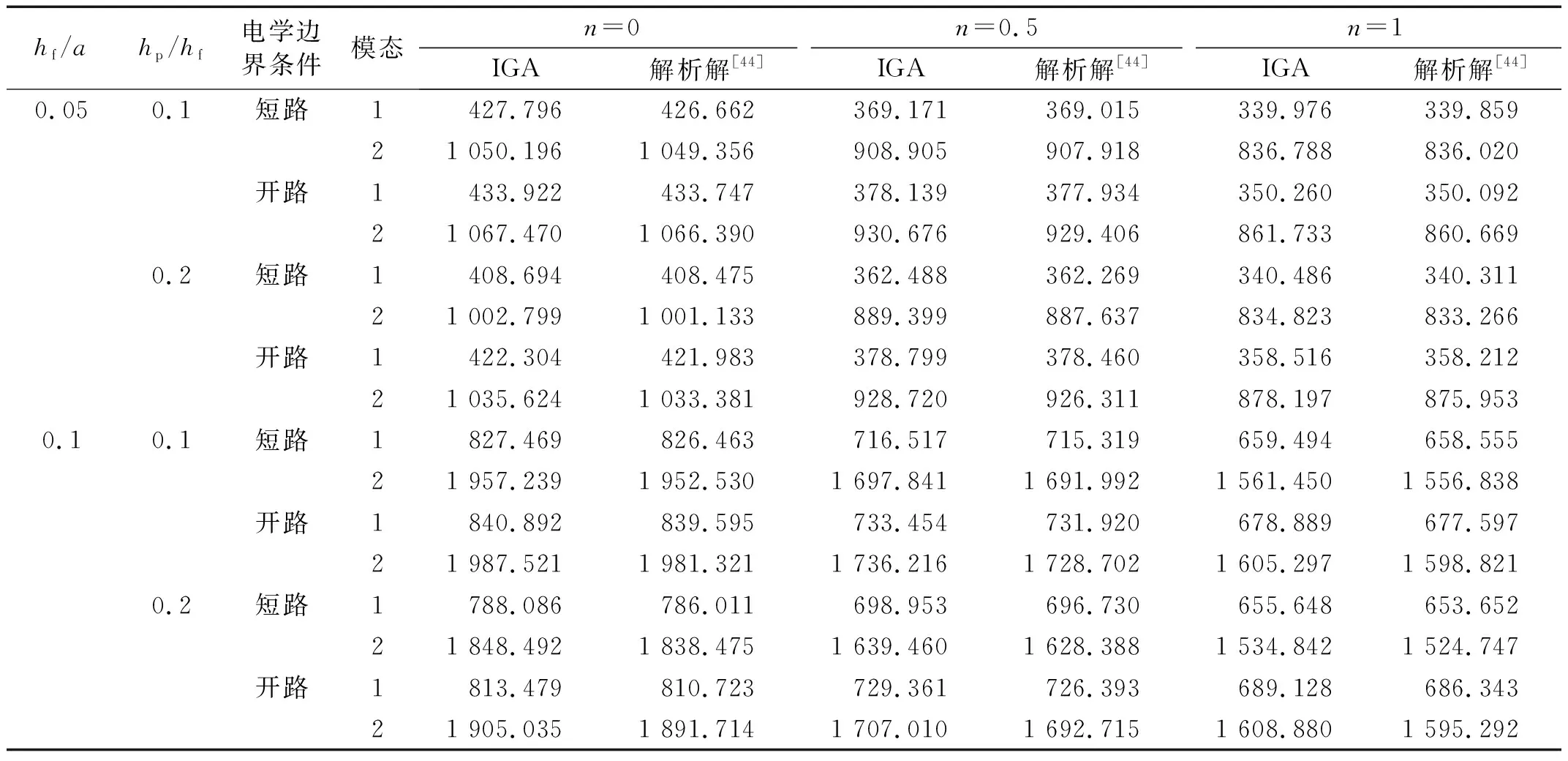
表4 短路和开路条件下，四边简支(SSSS) PFGP的前两阶固有频率

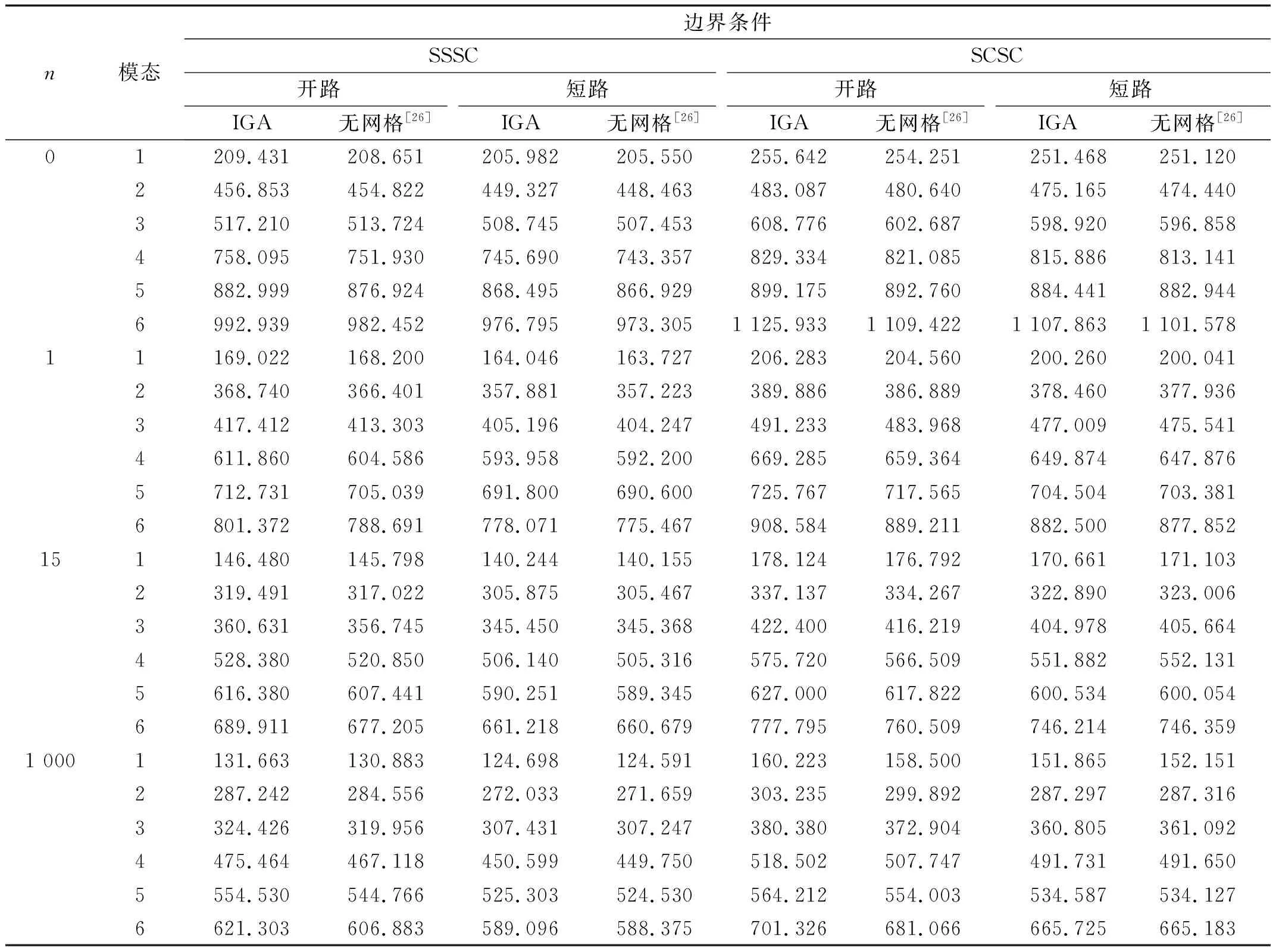
表5 机械边界条件为SSSC和SCSC的PFGP在短路和开路状态下前6阶固有频率

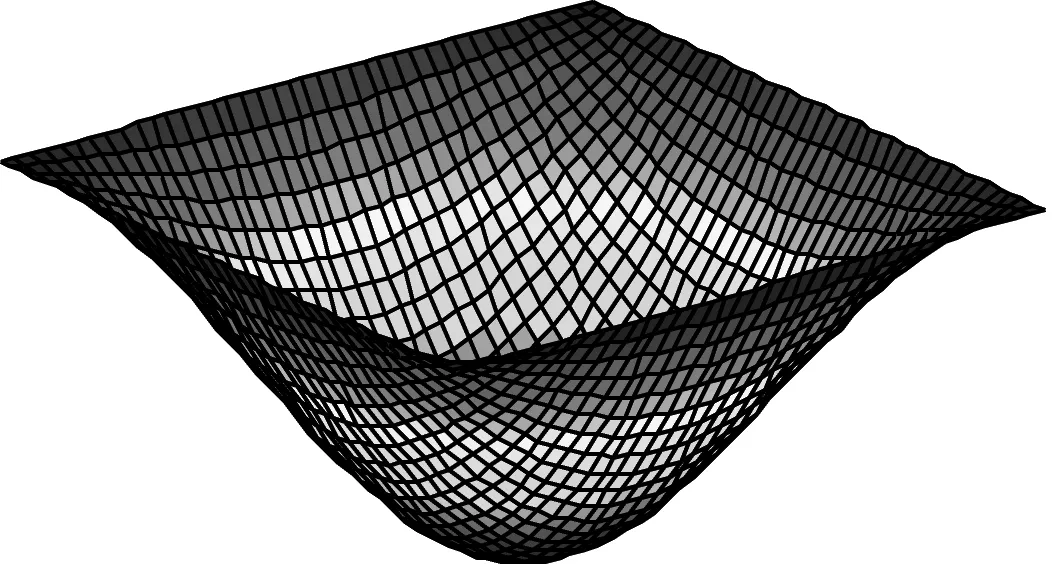
(a) 一阶振型

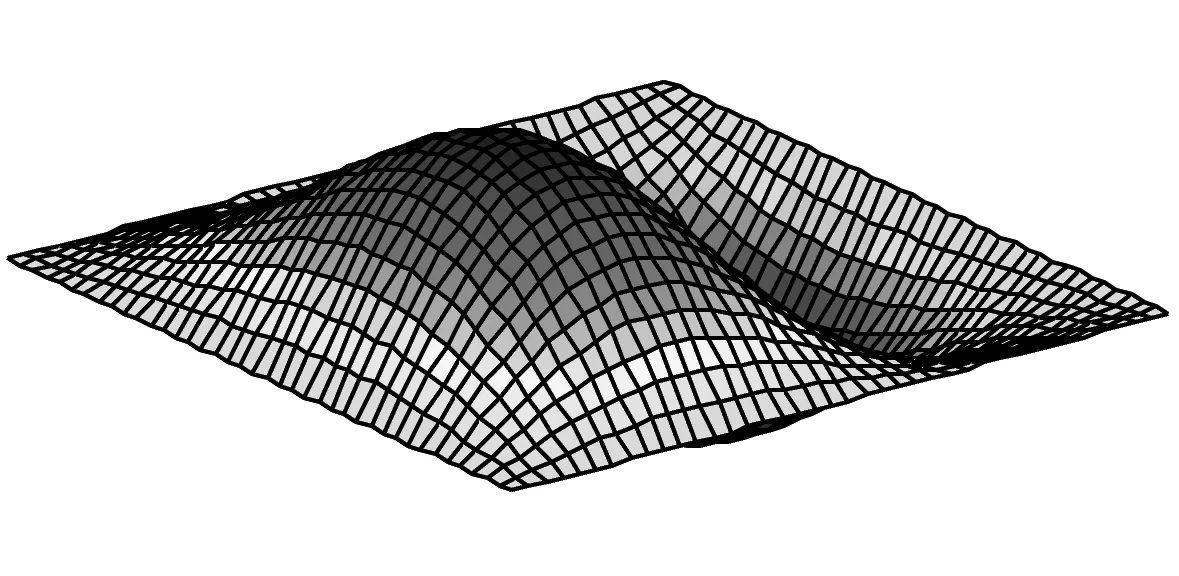
(b) 二阶振型

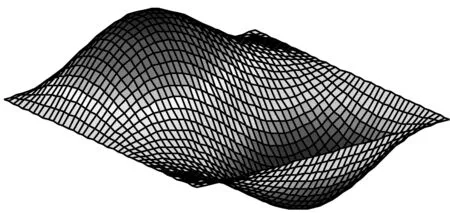
(c) 三阶振型

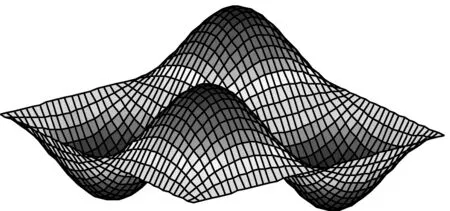
(d) 四阶振型

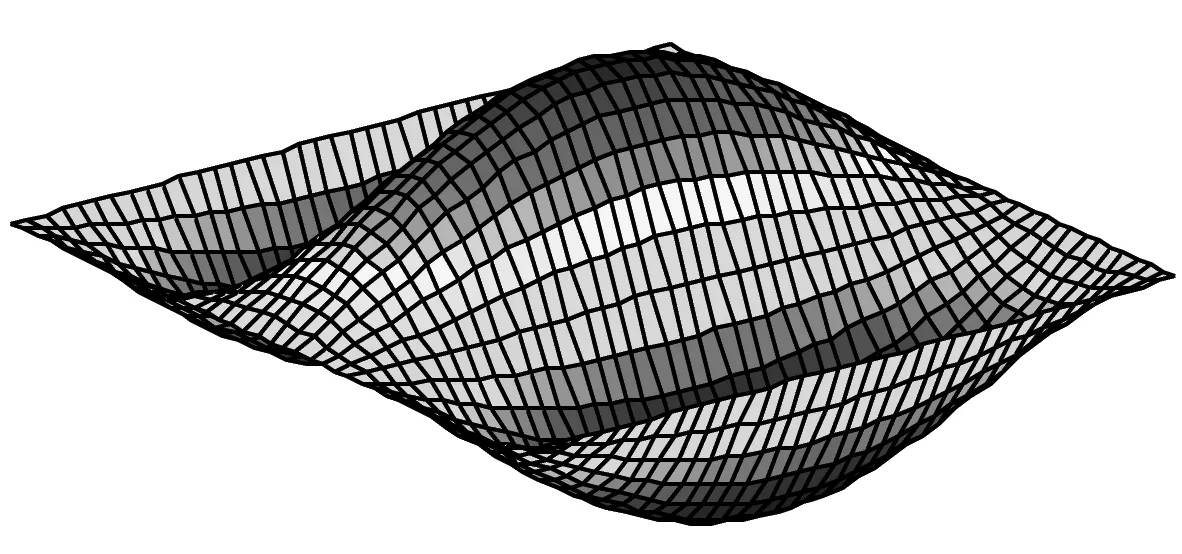
(e) 五阶振型

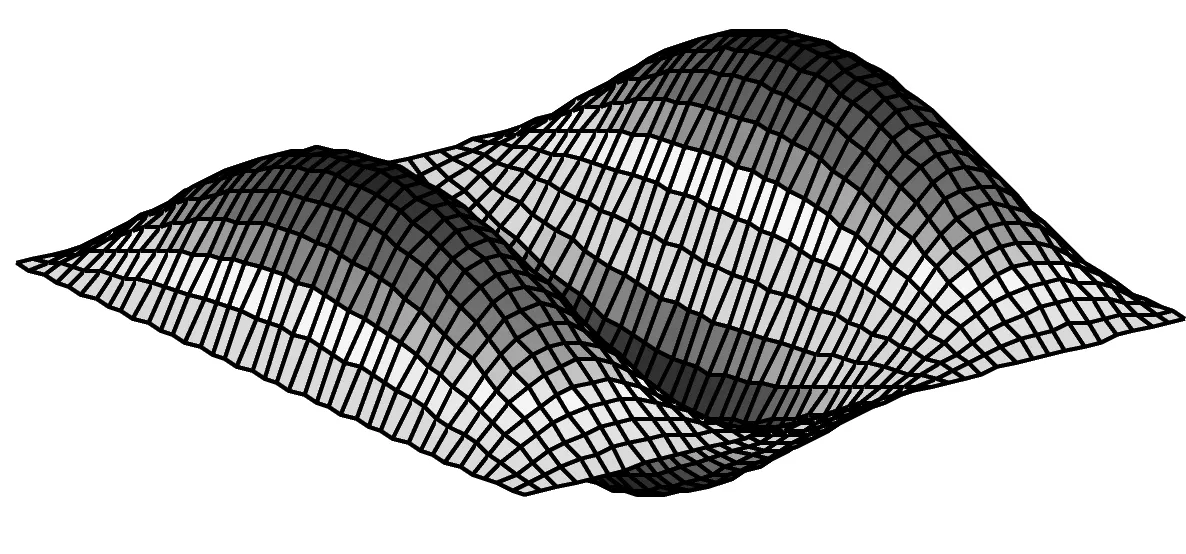
(f) 六阶振型

3.3 静态弯曲与变形控制

3.3.1 压电双晶悬臂梁的弯曲分析

如图4所示，尺寸为100 mm×5 mm×1 mm的压电双晶悬臂梁，其上、下层压电材料采用极化方向相反的PVDF材料。材料参数为E1=E2=2.0 GPa，G12=1.0 GPa，v12=0，e31=e32=0.046 C/m2，k11=k22=k33=10.62×10-9F/m。当对上下压电层施加外电场时，悬臂梁因逆压电效应而产生弯曲变形。

图4 压电双晶梁(mm)

在单位电压(1V)作用下，悬臂梁上不同位置的挠度值如表6所示，通过对比可知，本文方法与文献[45-46]的数值方法以及文献[47]的解析解结果基本吻合。

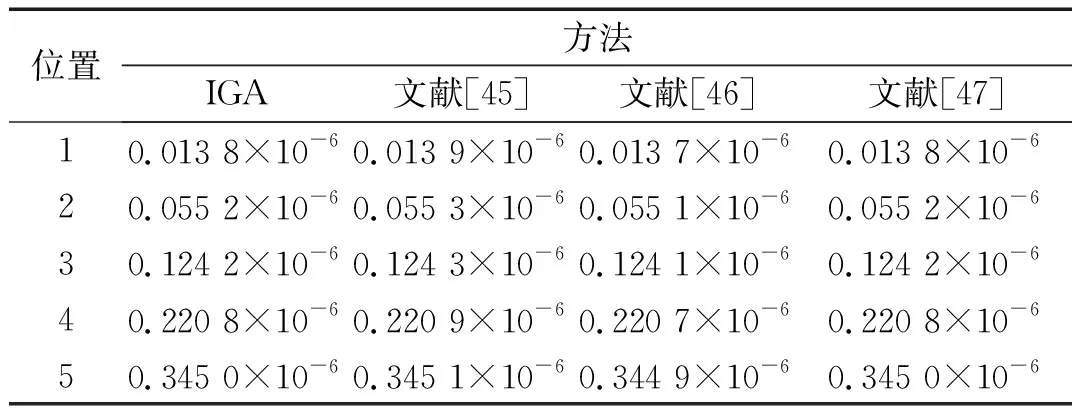
表6 单位电压下的压电双晶梁的挠度

如图5所示，随着输入电压的增大，压电双晶梁的中心线挠度也随之增大。不同电压作用下梁末端的挠度值如表7所示，对比可知，本文与文献[45,47]的计算结果基本一致。

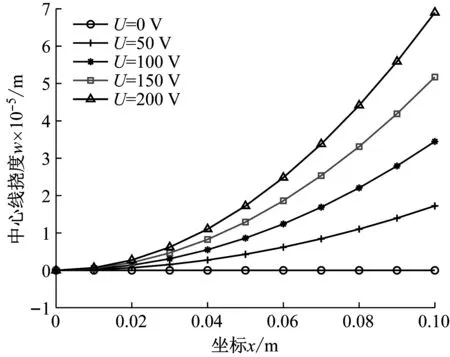
图5 不同电压作用下压电双晶梁中心线挠度

表7 不同电压下的压电双晶梁末端挠度

3.3.2 压电功能梯度方板的弯曲分析

本节对一个边界条件为CFFF的PFGP进行分析。板的材料和尺寸均与3.1节算例相同。

图6给出了板面受均布载荷q0=100 N/m2作用下，功能梯度指数n对板中心线挠度的影响。可以看出，随着n的增大，悬臂板中心线的挠度值逐渐变小，该结果与文献[8,48]的结果相吻合。图7为PFGP的上、下压电层仅受10 V的反向电压时的挠度值变化，此时，压电层均作为驱动器，即板的开环变形控制，可以看出本文方法与文献[36,48]趋势吻合。

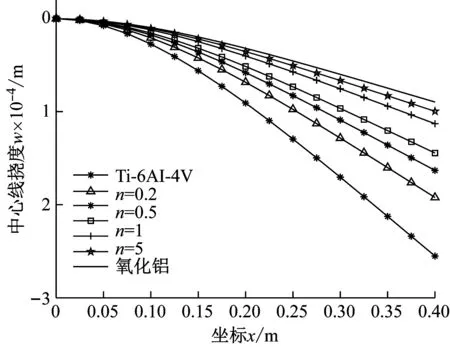
图6 均布载荷作用下n对悬臂板中心线挠度的影响

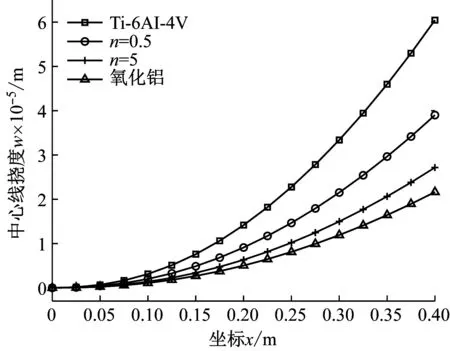
图7 悬臂PFGP在10 V电压作用下的中心线挠度

此外，为研究机电耦合情况下的挠度变化，对悬臂板同时施加q0=100 N/m2的均布机械载荷和不同的输入电压时板的中心线挠度变化如图8所示，可以看出，中心线挠度变化的趋势与文献[36,48]相吻合。表8统计了对应的末端位移值，可以发现，随着电压的增大，板中心线末端挠度值逐渐减小。

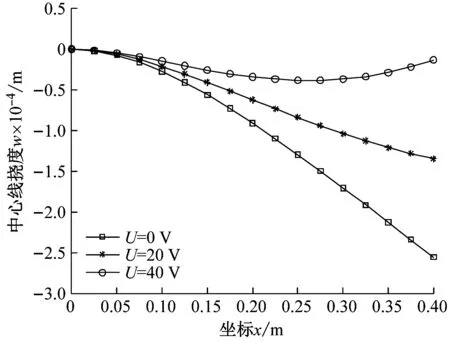
(a) n=0

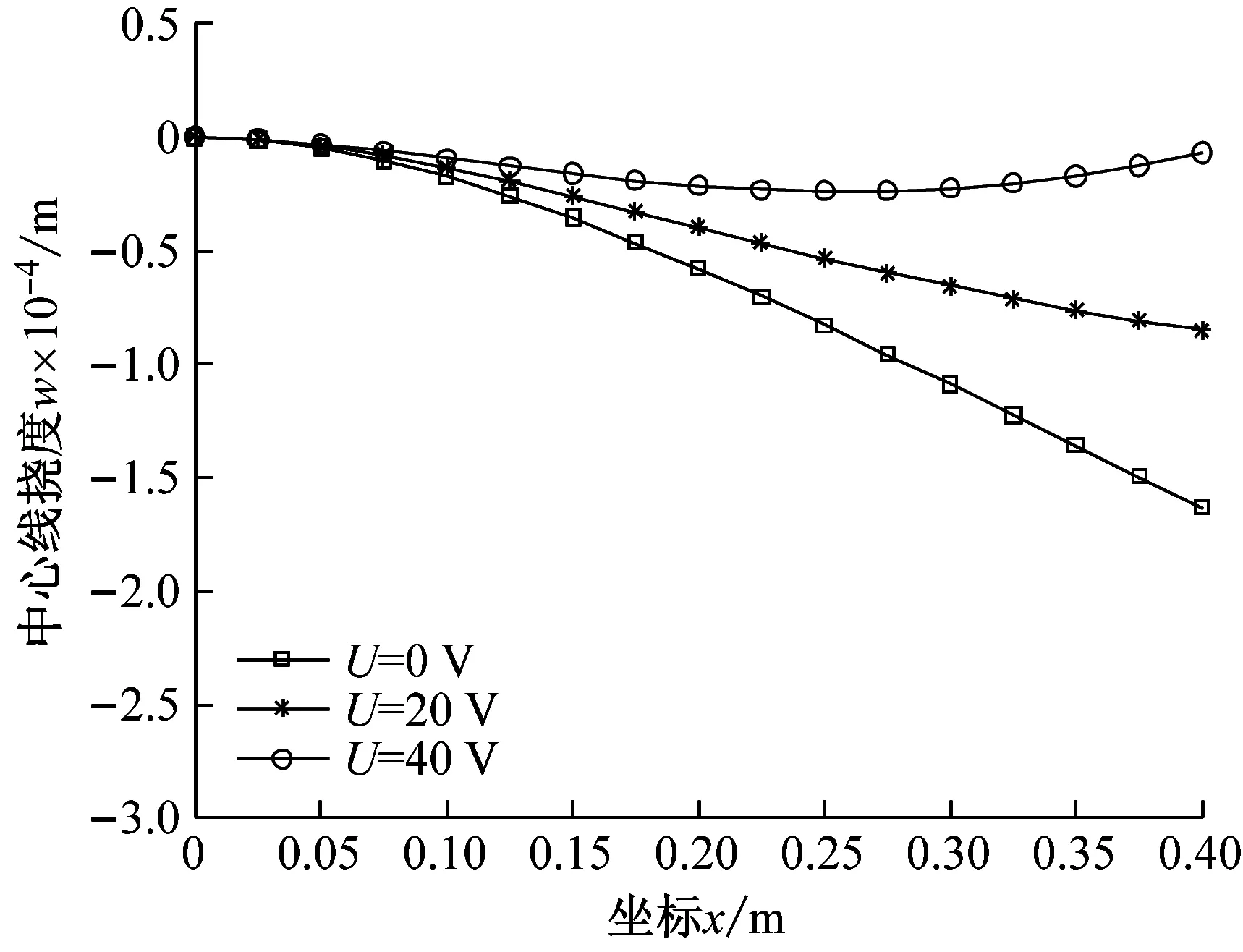
(b) n=0.5

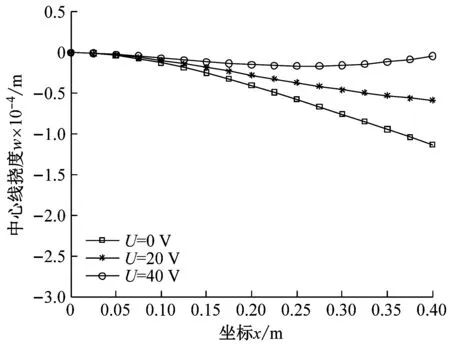
(c) n=5

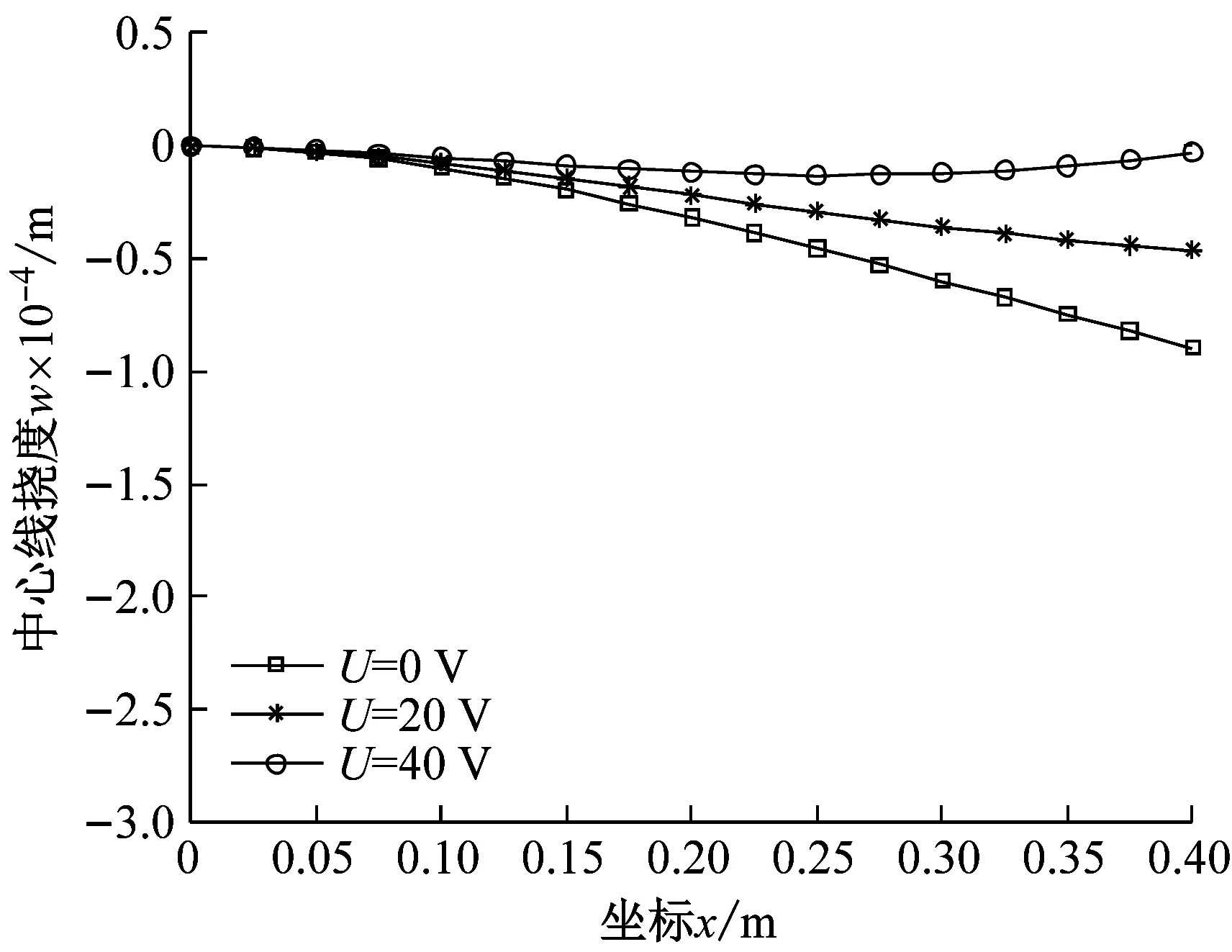
(d) n=∞

为探讨机械边界条件对PFGP形状变化的影响，图9分析了功能梯度指数n=2时，不同输入电压以及四种不同边界条件下指定位置的挠度变化情况。可以看到，随着电压的增大，挠度呈线性变化。值得注意的是，对于悬臂PFGP，板末端向上翘起(末端挠度值为正)；但对于边界条件为SFSF、SSSS、SCSC的PFGP，由于机械边界条件的改变，板中心向下凹陷(中心点挠度值为负)。产生这种现象的原因如图1所示，当上压电层的输入电压与极化方向相反时，逆压电效应使得其沿长度方向收缩。下压电层厚度方向的输入电压与极化方向相同时，其沿长度方向伸长。机械边界条件的改变使得板的弯曲方向发生了变化。

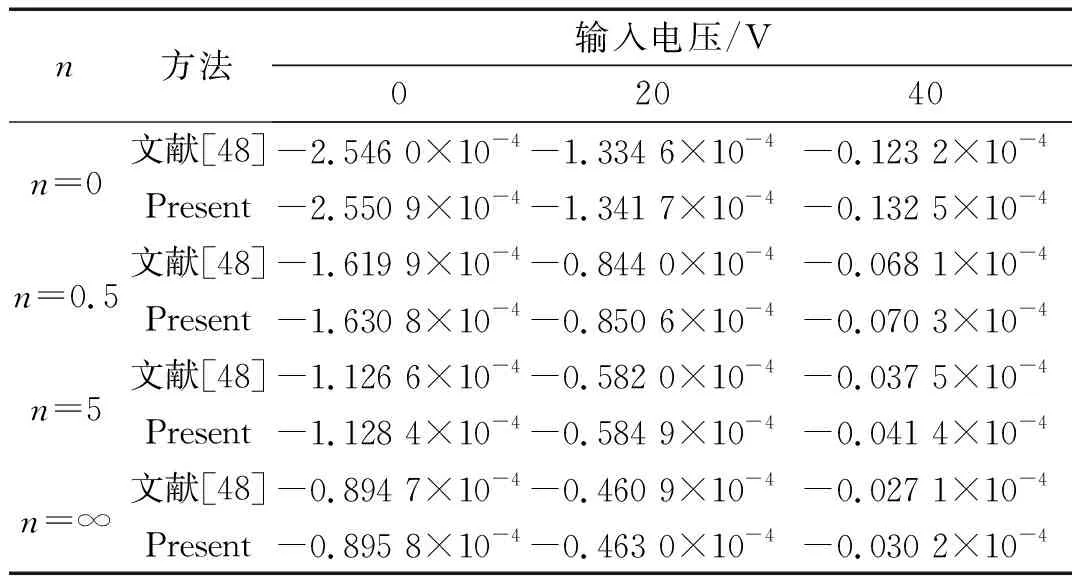
表8 均布载荷与不同电压作用下悬臂PFGP中心线末端挠度

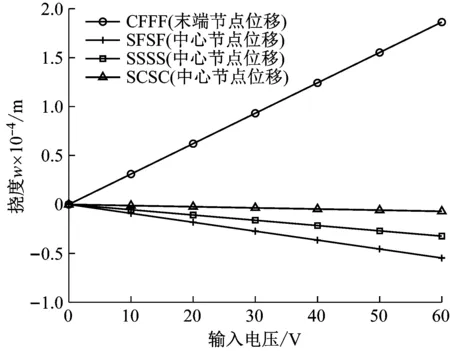
图9 不同电压作用下边界条件对PFGP挠度的影响(n=2)

3.3.3 悬臂压电功能梯度板的闭环变形控制分析

最后，分析了边界条件为CFFF和SSSS的PFGP的闭环变形控制问题。算例中，板的尺寸和材料与3.1节相同。上压电层作为驱动器，下压电层作为传感器。如图10、11所示，在机械均布载荷q0=100 N/m2作用下，随着增益Gd的增大，板中心线挠度逐渐减小。这是因为传感器层因机械变形(正压电效应)产生的输出电压经位移反馈控制增益Gd放大后作为驱动器层的输入电压。该输入电压产生相应的反驱动力抑制结构的变形。

4 结 论

本文为压电功能梯度板的静力学分析提供了一个新的高精度数值分析方法。该方法根据哈密顿变分原理以及相关压电方程，构建了三阶剪切变形理论下的功能梯度板等几何有限元形式。为全面探讨该数值方法的有效性，本文分析了自由振动的收敛性问题，并研究了功能梯度层的相关梯度指数n、宽厚比以及压电层与功能梯度层的厚度比对压电功能梯度板固有频率的影响。此外，文中对机械载荷、电载荷、机-电载荷下压电功能梯度板的静态弯曲响应也进行了全面讨论。最后，本文研究了压电功能梯度板的闭环变形控制问题。

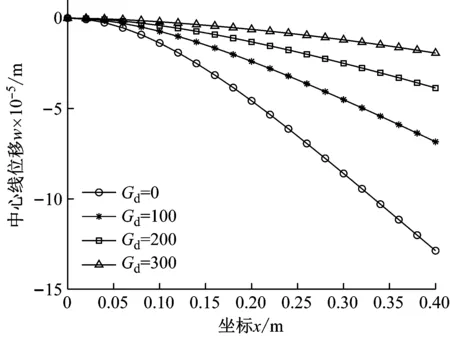
图10 反馈增益Gd对悬臂PFGP中心线挠度的影响

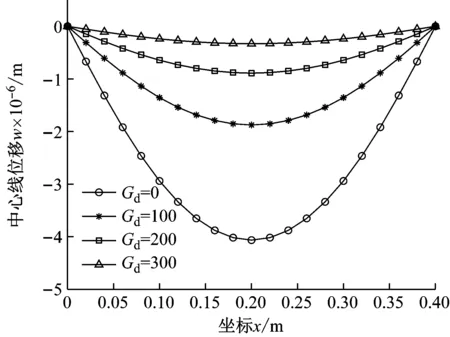
图11 反馈增益Gd对四边简支PFGP中心线挠度的影响

静力特性是压电功能梯度材料结构最基本的力学特性，但该材料的动力学响应亦是工程实际中经常面对的问题，因此，本文方法下的相关动力学研究是一个值得关注的课题。此外，在热环境下压电功能梯度材料的力学分析中，本文方法的适用性问题亦是一个值得关注的领域。