新课标下初中数学教学案例设计——以“探索勾股定理”为例

孙 悦，刘金魁

（重庆三峡学院，重庆万州 404000）

1 引言

《义务教育数学课程标准（2011 版）》中提出了义务教育阶段数学课程内容的核心概念，分别是数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识.这些核心概念全方位概括了中学数学教学工作中教师应该让学生具备的数学能力，在核心概念的指导下，教师应该摆脱传统的教学模式，重视对学生进行这十个方面的能力培养［3］.初中数学具有一定的理论性和抽象性，而信息技术拥有很强的实践性与创造性，将信息技术与初中数学教学相融合，可以更好的发展学生的十大核心概念.

2 教学案例设计

2.1 教学内容分析

本节课是部编版八年级下册第十七章勾股定理第一课时.本节之前学生已经学习了三角形一些知识，而勾股定理研究的是直角三角形三边之间特有的数量关系，将形与数密切联系起来，是解直角三角形的主要依据，在生产和生活实际中应用广泛.

2.2 教学目标

知识与技能：掌握一个定理——勾股定理，并会用定理解决简单问题.

过程与方法：经历一次由特殊到一般的探索过程，通过观察、思考、猜测、计算、推理、验证等活动过程，培养数形结合思想、渗透十大核心概念.

情感与态度：在探究活动中，激发学生求知欲，培养学生的合作交流意识和探索精神.

2.3 教学重难点

教学重点：勾股定理的内容.

教学难点：割补法构造图形.

2.4 教学过程

2.4.1创设情境，引入新课

设计意图：用PPT抛出一个目前生活中解决困难的实际问题图1，能够更直观、明确的引出“勾股定理”，从学生最熟悉的生活实际出发提出问题，体现数学的生活化和生活的数学化，贴近学生实际，利于学生体验、理解、思考与探索；更有利于培养学生的应用意识，吸引学生兴趣并引发学生思考.如学生在解答问题时遇到困难，从而引起学生的求知欲.

图1 关于勾股定理的实际问题

2.4.2自主探究，感悟新知

师：如果在任意一个直角三角形中还会有这种关系吗？

生：有的学生回答有，有的回答不知道.

图2 等腰直角三角形三边关系

设计意图：通过毕达哥拉斯和地砖的图片来讲述这个故事（图2），能够很好地吸引学生的兴趣，渗透数学文化，从而达到以毕达哥拉斯的发现启示学生直角三角形三边存在某种数量关系的目的.引导学生将直角三角形三边的数量关系向以直角三角形三边为边长的正方形面积联系起来，渗透转化思想，培养学生义务教育十大核心概念之一的几何直观.从而得到等腰直角三角形三边的关系，充分考虑本阶段学生学习的特点，符合学生的认知规律和心理特征.顺着等腰直角三角形三边的关系，提出所有的直角三角形三边是不是有这样关系.是特殊推到一般思路的体现，重在培养学生的推理能力.

2.4.3小组合作，探究新知

师：请同学们看课件上老师任意画的两个直角三角形，请同学们以前后四人为一小组展开讨论.

生：举手回答

师：那你们是怎么得到正方向C的面积呢？

生：有的是靠数格子大概得到，有的用到了“割”“补”法.

图3 以直角三角形三边为边长的正方形面积

设计意图：在课件上展示任意给出了两个直角三角形以及相应的表格，让学生分成小组进行讨论.避免了画图浪费时间以及不严谨等问题，抽几个代表说明他们的算法.主要培养学生的运算能力、合作交流能力，充分体现学生的主体地位.

师：让同学举手到黑板上书写计算过程并讲解，让学生自己判断、评价.

师：讲评学生的这种方法，给同学们讲解“割补法”（图4）.

师：用“割补法”算算并填表，同学们又会得出什么结论？

生：左图C 的面积为13，右图C 的面积为25.以直角三角形两直角边为边长的正方形面积之和等于斜边的正方形面积.

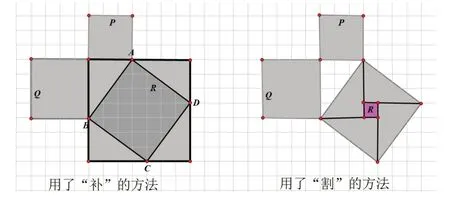
图4 割补法

设计意图：让同学们到黑板书写计算过程并讲解，能够锻炼同学们的胆量以及表达能力以及创新意识.在图片中突出显示能更加直观的展示“补”和“割”的地方.进而对以斜边为直角边的大正方形的面积计算.渗透了数形结合、转化等解题思想，把复杂的数学问题变得简明、形象，培养学生的空间观念和几何直观.根据学生给出的答案得到直角三角形三边向外作的正方形的面积关系，进一步让学生进行猜想直角三角形三边的数量关系，培养学生符号意识、数据分析观念和推理能力.

2.4.4归纳概括、讲解定理

师：你能用数学语言来表示吗？（放映课件）

生：SA+SB=SC,a2+b2=c2

师：我们得到的直角三角形三边之间的数量关系被称之为勾股定理.在黑板上板书勾股定理.

根据得到的三角形三边的数量关系给出勾股定理的定理.从而达到《义务教育数学课程标准（2011 版）》对第三学段探索勾股定理的要求，让学生经历观察、猜想、计算、推理、验证等活动过程.其中让学生用字母表示直角三角形三边关系培养了学生的符号意识，概括归纳定理培养了学生的归纳概括能力.最后在黑板上板书定理，吸收传统教学优点，强调本节课的重点，并能时刻出现在学生视线中，可以很好的巩固所学知识.

2.4.5学以致用、解决问题

师：学习了勾股定理，我们再回过头来看这道题，同学们现在能解决这个问题了吗？请你们在本子上算一算.教师巡视.

生：请两位同学上黑板板书过程

设计意图：回归本节课开始提出的问题，有始有终，让学生完整的体会发现、提出、分析、解决问题的过程.渗透数学模型思想，从具体情境中抽象出数学问题，用数学符号建立方程等；培养学生的应用意识，有意识地用数学概念、定理等解决现实世界中的问题（图5）.

图5 勾股问题的解题过程

2.4.6共享收获、布置作业

师：现在我们来回顾下本节课学习了什么内容？用到了哪些思想方法？

生：回答勾股定理、“割补法”、数形结合思想等.

师：现在我们大家一起来看个一分钟左右的小视频（图6），看完视频后请同学们课后自己探索勾股定理的证明方法，至少一种.

图6 勾股定理的及证明的小视频

设计意图：带领同学回顾勾股定理以及本节课所学思想方法，用一个小视频来结束本课既可以缓解课堂氛围，又给学生留下作业思考，提起学生学习兴趣、引发学生的数学思考、鼓励学生的创造性思维.

2.5 教学反思

在这个教学案例中用问题导入法引出课题相比于传统的直入主题更能够启发学生的求知欲、培养学生的应用意识；而用课件的方式展示能够更加直观、吸引学生.再辅以关于毕达哥拉斯及勾股定理的图片，渗透数学文化.辅以课件讲解割补法，突出显示鲜明不单调，能更好突出割补的部分，使得原先复杂的问题变得简单直观.在课尾以一个视频结束，可缓解学生疲劳，同时也渗透了数学史、为下节课的内容做了铺垫，自然而然地让学生课下带着思考去探索.

3 总结

《义务教育数学课程标准（2011 版）》提出的十大核心概念是各个专家学者在多年义务教育工作中所总结出来的，概括了义务阶段教学工作中我们应该让学生具备的数学能力，在信息技术环境下，我们更应该重视对学生进行十大核心概念方面的培养，并付之行动.十大核心概念既相互独立、又相互交融，是一个有机的整体［4］.因此想要把十大核心概念更好的在教学中体现出来，无疑结合信息技术、改变传统的教学方法是必不可少的.

本文秉承新课程理念对初中数学八年级下册勾股定理进行教学设计，结合了多媒体课件和新课标理念下十大数学核心概念，在教学过程中渗透数学思想方法、核心概念，有利于培养学生的创造性思维、良好的数学学习习惯，更有利于培养学生动脑思考、自主探索的能力.