指数回归模型下的渐近局部D -最优设计

（凯里学院，贵州凯里 556011）

1 指数回归模型

在社会生产实践中，为了得到准确的统计结论，一方面有赖于精确的统计推断方法，而另一方面则需要试验设计来合理安排试验，以便于统计推断.基于最小二乘原理，回归试验设计考虑的模型为：

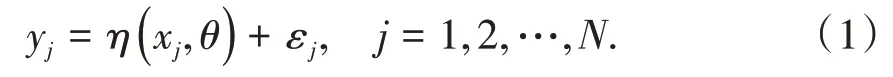
Y1,Y2…YN为试验结果为未知待估的参数向量为给定的试验条件，X为拓扑空间上的紧集，称之为设计域，在模型（2）下，一般定义为随机误差向量，满足为N阶单位阵.

模型一般还假定ai≠0，λi＞0，i=1,2,…,k，

设若进行N次试验，假设在试验点xi处进行了ri次试验，记为试验点xi的为权系数，记x1,x2,…,xn中的n个不同的设计点为0 ＜x1＜x2＜…＜xn，定义一个带有离散型概率测度的设计为：

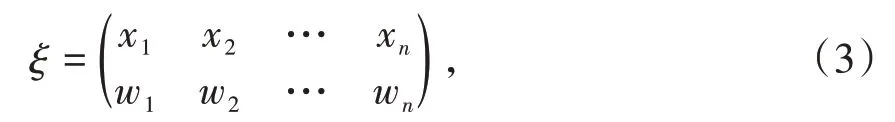
称ξ∈Ξ 为一个具有测度的n点设计，Ξ 称为设计空间.记是N次试验下参数向量θ的最小二乘估计，可表示为其中Yij是在试验点xi处进行的第j次试验的结果，m=2k即未知参数的个数.且在模型下的最优试验设计一般与模型的信息矩阵有关，Fedorov［2-3］中给出了含有未知参数的Fisher信息矩阵的定义为：

注意到对于ξ∈Ξ，参数a1,a2,…,ak对detM(ξ,θ)值没有影响.不失一般性，在D -准则下，我们令a1=a2=…=ak=1，并给定参数Λ=一个初值在的条件下，可得到回归模型（2）的信息矩阵与线性模型（9）的信息矩阵形式一致，

这里β1,β2,…,β2k是待估参数，而λ1,λ2,…,λk假定为已知的.下面就在给定Λ初值的条件下讨论模型（2）的局部渐近D-最优设计.

2 渐近局部D-最优设计

其中m=2k，如果是D-最优设计，则称是在Λ 下的局部最小支撑D-最优设计（Local Doptimal Minimum Support design，简称为LDMS）.

3 Monte-Carlo方法构造试验点样本

使用［4 -5］中的拟分量变换方法，可以将一维区间上的随机点集.在回归模型（2）中，由于设计域X=[0,∞)，由实践经验可确定参数Λ 的初值，并将设计域控制在某一个范围之内，例如令X=为一个闭区间，由于一般LDMS 设计都定义x1=0，我们也可以将设计域的左端点定义为一个非零正数a.

为计算信息矩阵M(ξτ,Λ)，我们首先使用Mon⁃te-Carlo 方法构造出一系列在试验域中的试验点.定义一个随机变量X∼U[a,b]，且由X生成n×(m-1)个随机数，这里m代表了回归模型中所含有的未知参数个数，n表示需要模拟试验的次数.将这些数分为n组，每组有m-1个数，记为

记Rj为矩阵R的第j行元素，我们也称Rj为第j个随机样本.将Rj中元素从小到大排列为

除去0元素之外的另外m-1个元素，在第j组样本中可视作该样本下的第i个次序统计量，则由均匀分布的性质易得：

注意到μ1,μ2,…,μm-1是区间[a,b]中的m-1个点，这m-1个点把[a,b]分为m个长度相等的区间.当n→∞时，应有Zi依概率收敛于μi，这样就使得随机生成的试验点均匀的散布在区间[a,b]上，

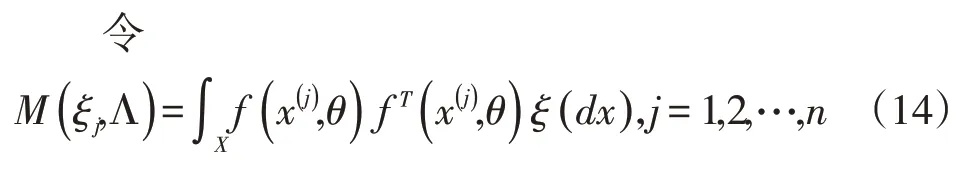
表示第j个随机样本下的信息矩阵.

设若存在一个LDMS设计ξ∗∈Ξ，则应有

所以，随着随机样本量的增多，我们能从中找到一组数值，使得其充分接近最优试验点.

例我们考虑含有6 个未知参数的指数回归模型.其形式为

为此需要选择6 个试验点，其中第1 个试验点为0，记试验点为τ=(0,τ1,τ2,…,τ5)，则6 点试验可表示为：

由（11）可知，在设计ξτ下，矩阵Fτ为

可见，如果要求出出det(Fτ)关于τ的显式表达是比较困难的.下面我们使用Monte-Carlo 方法构造试验点样本.由之前所讨论的，首先生成n×5个随机数，然后与n维零向量合并为一个n×6 阶矩阵，记为R，以矩阵R的每一行作为一组随机数代入模型（15）进行计算，得到n个行列式值，分别记为：

其中Fτ(ξj,Λ)的形式如（13）中定义的Fτ，由于信息矩阵的行列式由决定，即与的正负无关.将各行列式值从小到大进行排列，得：

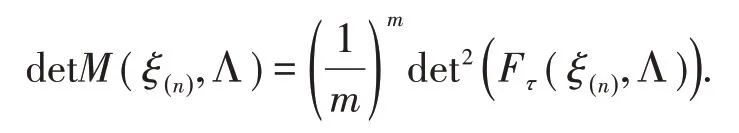
本文通过Monte -Carlo 方法生成闭区间设计域X=[a,b]上的若干随机数，然后利用这些随机数进行模拟，当模拟次数很大时，信息矩阵的行列式值和它的逆矩阵的迹都会稳定在一个固定值附近.如果设计点是已经固定化的，则使用文［6-7］的方法，将测度向量视为一个单纯形上的混料点，然后执行随机搜索算法，即可以确定最优设计.

对于闭区间设计域上，使用Monte-Carlo 方法获得渐近最优解的过程并不复杂，易于实现.但Monte-Carlo 方法会随着区间长度的增加，求解近似解的效果会越来越差，并且很不稳定，关于这一系列问题都有待进一步研究.