矿用直驱永磁电机磁热双向耦合分析

孙重阳，冯桂宏

(沈阳工业大学 电气工程学院，沈阳 110870)

0 引 言

煤炭是我国的重要资源，随着近年来电力电子技术及装备制造业的快速发展，越来越多的煤矿企业也在追求着采煤工作的高效化、智能化。永磁电机的气隙磁场是由永磁体本身建立的，所以较异步电机来说可以做成多极低速大转矩直驱，实现动力与负载直接接触，从而使系统传动效率最大且提高运行稳定性，目前已经得到广泛的推广与应用[1-2]。

低速大转矩直驱永磁电机的转矩密度较大，在电机运行时发热量较大，同时对于矿用防爆电机来说，由于机壳隔爆面的存在，使得电机的密封性更强，散热效果较普通电机更差。温升更高，影响电机的使用寿命和驱动系统运行稳定性。同时对于煤矿井下这种特殊的工况条件，电机表面可能会附着大量的煤粉及其他可燃物，一旦电机表面温度过高达到可燃物的燃点，将造成十分严重的后果，在国标中也严格规定了矿用防爆电机表面允许的最高温度。所以在电机设计工作中，也必须要对电机的运行温度进行严谨的分析与计算。

热网络法是目前电机温升计算比较常用的方法。它是应用图论原理构造电机网络拓扑结构进行热场分析。该种方法计算速度快、计算精度较高。除此之外还有简化公式法和有限元法[3]。

电机运行发热的主要原因是定子绕组、定转子铁心、永磁体等产生的损耗。同时这些结构的材料属性也会随着温度的变化而变化，所以单一的分析电机的电磁场或温度场不足以准确反映电机实际运行工况，需要将电机的磁热模型进行耦合分析。

1 矿用直驱永磁电机模型及参数

本文分析矿用直驱电机模型为内置切向式磁路结构，绕组为多极少槽的真分数槽集中绕组结构，电机主要参数如表1所示，图1给出了电机的二维模型图。

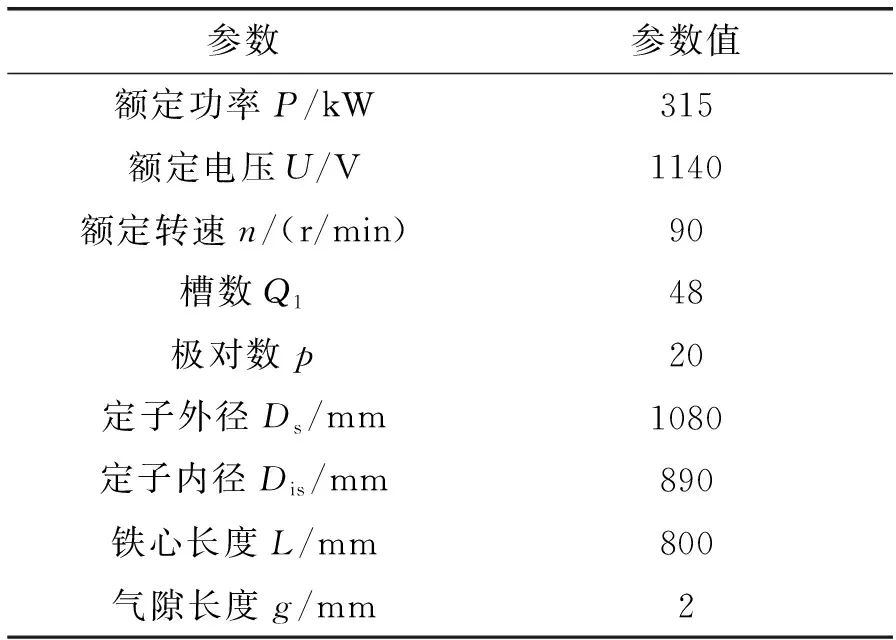
表1 电机参数

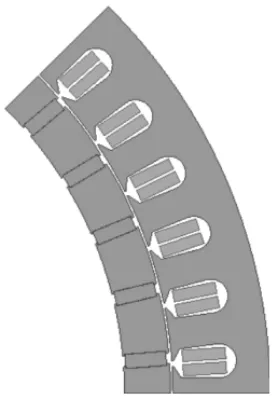
图1 电机二维模型图

图2给出了电机的磁密与磁力线分布云图，由图可知，电机齿部磁密在1.6T左右，未达到饱和，仅有少量磁力线未经过气隙与定子交链，电机磁极结构设计合理。

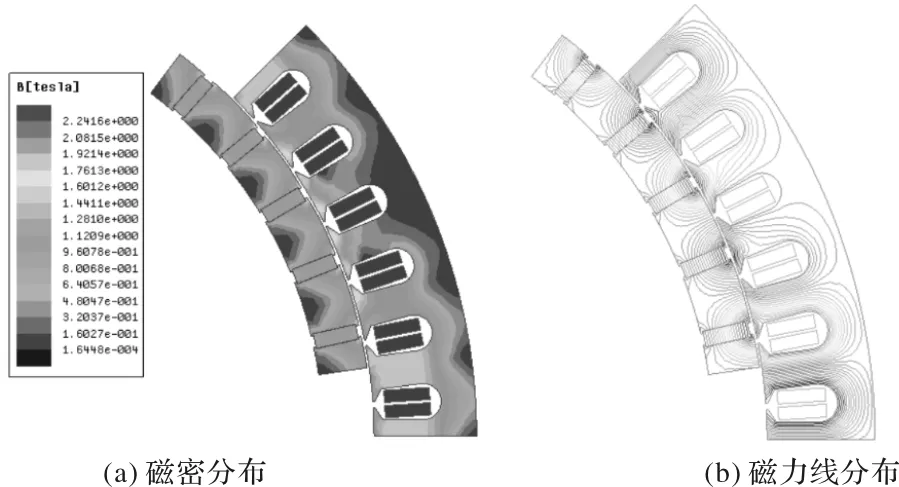
图2 有限元分析结果图

2 基于热网络法电机磁热双向耦合

2.1 电机热网络模型构建

在构建电机等效热网络模型时，首先应确定电机的传热过程，对于本文分析的矿用永磁直驱电机，通过在机壳内部的轴向水道中的冷却介质流动来冷却电机内部产生的热量，传热过程主要包括电机内各个结构间存在温度梯度的热传导过程以及冷却介质与电机结构间的热对流过程。其次分析电机运行时的热源分布，最后利用正交网格剖分将电机内温度场剖分为多个区域，定义各个剖分域内中心点为一温度节点，并将各个节点间根据电机传热过程的不同用传导热阻或对流热阻联接。构成电机温升的等效热网络图[4]。图3给出了本文分析电机的等效热网络图。

图3 等效热网络模型

图3中，a、b、c为冷却介质边界节点；1、2对应为电机端部与机壳间存在的气体温度边界节点；3、4、5对应电机轴向水冷机壳节点；6、7、8对应定子铁心轭部节点；9-13对应为定子绕组节点；14、15、16对应定子铁心齿部节点；17、18、19对应转子铁心节点；20、21、22对应永磁体节点；23-28对应转轴节点。

2.2 传导热阻分析计算

由建立的电机等效热网络模型可知，热传导过程主要存在定子轭部、定子齿部、定子绕组、转子铁心、永磁体5个结构之间，计算热阻时一般将导热结构简化等效为平板与管型两种导热模型[5-6]，其中，平板导热模型热阻可表示为

(1)

电机机座外壳、定子轭部等近似为空心圆柱体的导热结构一般采用圆管型导热模型，其热阻为

(2)

式中，Q为热量；λ为导热系数；S为导热面积；L为导热长度；r1、r2分别为管型等效模型的外径与内径。上述5个结构热阻的分析计算如下。

2.2.1 定子轭部

定子轭部的热传导路径主要为径向传导到机壳、定子槽、定子齿以及轴向定子轭部自身传导。

定子轭部节点6与机壳节点3的传导热阻为

(3)

式中，λs1、λg、λFe分别为径向定子硅钢片、空气、机壳的导热系数；hj为定子轭部高度；L63为定子铁心装配间隙，可由经验公式计算；DFe为机壳外径；hFe为机壳厚度。

定子轭部节点6与定子绕组节点10的传导热阻为

(4)

(5)

式中，δi为定子槽内等效绝缘厚度；λi为绝缘材料散热系数；hcu为定子绕组等效高度；r为梨形槽槽底圆半径；

定子轭部节点6与定子齿部节点14的传导热阻为

(6)

式中，bt为定子齿宽。

轴向定子轭部节点6与节点7自身传导热阻为

(7)

式中，λs2为定子轴向硅钢片导热系数。

2.2.2 定子绕组

定子绕组的热传导路径主要是径向定子绕组传递到定子齿部、定子轭部，轴向槽内绕组传递到绕组端部以及槽内导体自身传导。其中定子绕组节点10与定子轭部节点6的热阻

R106=R610

(8)

定子绕组节点10与定子齿部节点14的传导热阻为

(9)

(10)

式中，bcu为槽内绕组等效宽度；hs为定子槽高度。

轴向定子绕组节点10与节点11的自身传导热阻为

(11)

式中，λcu为铜导热系数；d为线圈裸线直径；Ncu为定子槽内绕组匝数。

轴向定子绕组节点10与绕组端部节点9的热阻可表示为

(12)

式中，L1为定子绕组端部长度。

2.2.3 定子齿部

定子齿部的热传导路径为径向传导到定子轭部、定子绕组以及轴向定子齿部自身传导。其中，定子齿部节点14与定子轭部节点6的传导热阻

R146=R614

(13)

定子齿部节点14与绕组节点10的传导热阻

R1410=R1014

(14)

轴向定子齿部节点14与节点15的热阻为

(15)

2.2.4 转子铁心

转子铁心的热传导路径主要为径向传递到永磁体以及轴向自身传递。转子铁心节点17与永磁体节点20的热阻可表示为

(16)

式中，λr1、λPM分别为径向转子硅钢片、永磁体导热系数；br为转子磁极冲片等效宽度；bm为永磁体宽度；hm为永磁体厚度。

轴向转子铁心节点17与节点18的热阻为

(17)

式中，λr2为转子硅钢片轴向导热系数；S1718为转子铁心导热面积。

2.2.5 永磁体

永磁体的热传导路径主要是径向传递到转子铁心以及轴向自身传递。其中，永磁体节点20与转子铁心节点17的热阻

R2017=R1720

(18)

轴向永磁体节点20与节点21的热阻可表示为

(19)

2.3 对流热阻分析计算

由等效热网络模型可知，热对流过程主要存在于水冷机壳传热、定子绕组及轭部端部与端盖和铁心间空腔传热、定转子铁心气隙间传热[7-9]。采用牛顿散热定律解决热对流问题，散热热阻可表示为

(20)

式中，αt为散热系数。

机壳节点3与冷却介质温度边界a的对流热阻可表示为

(21)

(22)

式中，SFe为水冷机壳面积；α3a为水冷对流散热系数；u为流体速度；d为冷却水道直径；λL、μ、ρ、cp分别为流体导热系数、流体粘度、密度和比热容。

定子轭部节点6与端部气体边界节点1的对流热阻可表示为

(23)

(24)

式中，αd为电机端部散热系数；v为电机转子线速度。

定子绕组端部节点9与端部气体边界节点1的对流热阻可表示为

(25)

式中，C为定子线圈外包绝缘后表面周长。

定子齿部节点14与电机气隙的对流热阻为

(26)

式中，αg为电机气隙散热系数，可由雷诺数Re、泰勒数Ta及努塞特数Nu计算确定。

(27)

(28)

(29)

(30)

式中，υa为空气粘滞系数；rm为平均气隙半径；λg为气隙导热系数。

转子铁心节点17与电机气隙的对流热阻为

(31)

式中，Dr为转子外径。

根据等效热网络建立电机稳态热平衡方程矩阵

T=RW

(32)

式中，R为热阻矩阵；T为电机内温度节点列阵；W为电机热源列阵。

2.4 电机热源分析

2.4.1 定子绕组铜耗

定子绕组铜耗主要与定子绕组的电阻值大小有关，定子绕组可由式(33)计算：

(33)

ρ=ρ20[1+α(t-20)]

(34)

式中，ρ为铜的电阻率；ρ20为铜在20℃下的电阻率；α为铜电阻的温度系数；Lav为线圈平均半匝长；N为每相串联匝数；a为并联支路数；Ac为铜线截面积；t为预估电机运行温度；所以，定子绕组铜耗可以表示为

(35)

2.4.2 铁心损耗

根据经典Bertotti损耗分离模型，忽略集肤效应的影响，电机的铁心损耗主要由磁滞损耗、涡流损耗及附加损耗构成，可由式(36)计算[10]

(36)

式中，Kh、Kc、Ke分别为铁心材料的磁滞损耗系数、涡流损耗系数和附加损耗系数；Bm为磁通密度幅值，可表示为

(37)

式中，bm0为随温度变化永磁体空载工作点，αBr为可逆温度系数；IL为不可逆损失率；Br20为在20℃时的剩磁；Am为每极磁通面积；σ0为空载漏磁系数；αi为计算极弧系数；i为极距；Lef为电枢计算长度。

2.4.3 永磁体涡流损耗

本文分析电机的额定频率较低，气隙磁场畸变率较大，同时变频器在低频时也会增加输出谐波含量，所以定子电流会产生很强的谐波磁动势，从而引起永磁体产生涡流损耗。涡流损耗为[11]

(38)

式中，Jn(t)为涡流密度；σ为永磁体电导率；ρPM为永磁体电阻率。

由以上对电机热源的分析可知，电机的各部分损耗都会随着温度的变化而变化。

2.5 磁热双向耦合分析

磁热耦合分析方法分为单向耦合与双向耦合两种[12]，单向耦合也称为顺序耦合指，先通过电磁场计算电机定子绕组铜耗、铁耗、永磁体涡流损耗等作为温度场分析的热源，然后通过对电机各个材料散热系数、导热系数等温度参数的设置以及冷却结构的设计，最终分析求解出电机的温升。单向耦合的设置比较简单，求解速度较快。但是也存在一些问题。在电机的电磁场分析过程中，需要预估电机在稳态运行时的定子绕组温度与永磁体工作温度，经电磁场分析后的定转子铁心损耗与定子绕组铜耗也都是在预估的温度值下计算的。但是由上文热源分析可知，永磁体的负载工作点、计算剩磁密度会随着温度的变化而变化，定子绕组所用铜材料的电导率也会随着温度的升高而降低，当电机的计算温度与预估温度相差较大时，这会直接影响电机稳态运行性能，从而影响电机各部分损耗计算的准确性，进而对电机温升的计算造成影响。如果电机的工况条件对电机稳定运行时的温升要求严格，那么在电机设计的过程中，仅进行电机磁热单向耦合分析是不严谨的。

磁热双向耦合分析过程如图4所示，电机的电磁场与温度场同时进行分析计算并互相迭代更新。由电磁场仿真分析得到的各部分损耗作为热源导入到温度场进行电机温升计算，而由此计算得到的电机各结构温度又导入到电磁计算单元中以精确模拟不同温度下材料特性的变化，并得到此时电机性能及损耗的计算结果。上述耦合计算过程将进行连续迭代，直至电机温度及损耗的计算结果达到收敛值。从而得到电机温升的准确计算。基于Motor-CAD建立此电机磁热耦合分析模型，如图5所示。

图4 电机磁热双向耦合分析过程图

图5 电机磁热耦合分析模型

电机冷却方式采用轴向机壳水冷，在机壳内部串联布置42个冷却水道，冷却水流量为1.8m3/h，进水口温度为25℃，轴向水道如图6所示。

图6 机壳轴向水道

定子绕组所用漆包线及绝缘材料均为H级绝缘，最高耐温150℃，磁钢牌号为N38SH，最高工作温度为150℃，设定电机稳定运行的温度为90℃，分别进行电机磁热单向与双向耦合，电机各部分损耗计算结果对比如表2所示。

表2 电机损耗结果

由表中数据可以看出，电机磁热单向耦合与双向耦合计算出的电机各部分损耗有所差异，而这种差异也会使电机的温度场分析存在误差。所以，本文采用磁热双向耦合方法对矿用直驱永磁电机进行温度场仿真分析。分析结果如图7所示，其中图7(a)为电机径向关键节点的温度分布，图7(b)为电机轴向关键节点的温度分布。电机主要结构温度如表3所示。

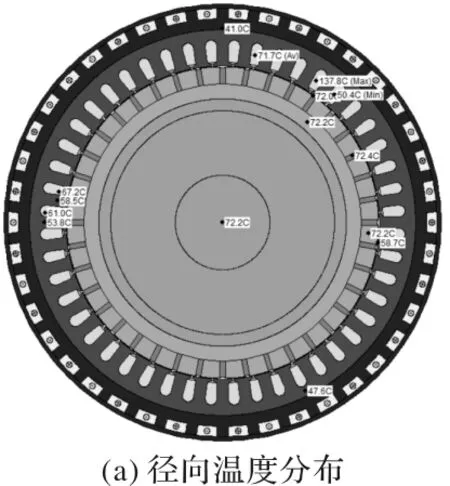
图7 电机稳态运行温度分布

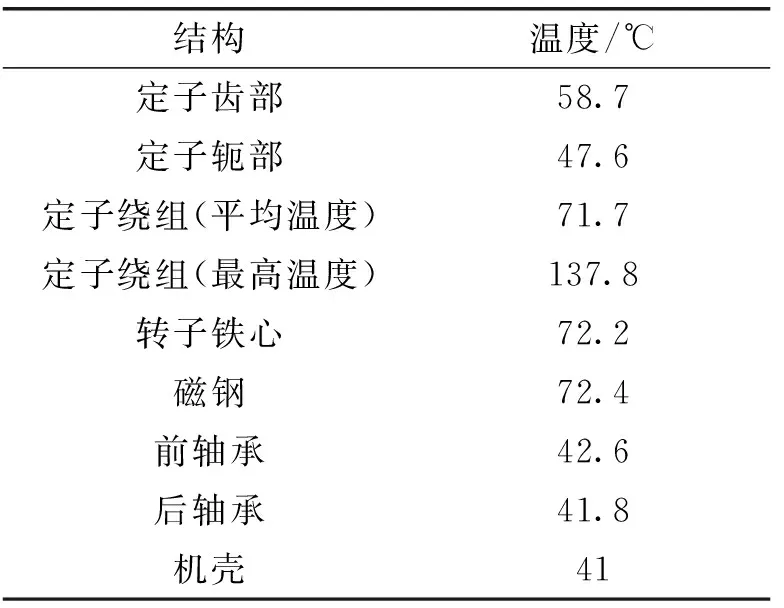
表3 电机主要结构温度仿真结果

由表中数据可知，在电机达到稳态运行时，电机主要结构温度均在正常范围，且留有较大裕度，电机可以长期稳定高效运行。

3 实 验

根据电磁设计方案进行样机的生产，待电机总装后，搭建如图8所示的实验平台进行电机实验，图8中，左侧为陪试机，右侧为实验样机。样机右下部为冷却水进出口，其中上部为冷却水进口，下部为冷却水出口。定子绕组测温元件PT100预埋于三相绕组中。

图8 电机对拖实验平台图

控制陪试机给实验样机施加额定转矩负载，连续运行三个小时，电机主要结构温度记录如表4所示，记录数据表明，样机运行平稳，电机进出水口、定子绕组、机壳及前后轴承温度均处于正常范围内，同时，将实验记录与仿真数据进行对比，我们可以看到，经过电机磁热双向耦合计算出的电机主要结构温度与样机实验后测得的温度十分相近。误差在5%以内。

表4 电机实验数据记录

4 结 论

利用Motor-CAD建立了电机的等效热网络模型，并采用有限元分析法与热网络法对电机进行了电磁场与温度场双向耦合分析，得到电机稳态运行温度，通过样机实验验证了电机和冷却系统设计的合理性，同时也验证了磁热双向耦合分析电机温度场方法的准确性，为今后电机稳态运行温升计算及冷却系统设计提供了一定的借鉴经验。